6.8: Teorema de Dilworth para órdenes de intervalo
- Page ID
- 118418
Como se comentó anteriormente, aún no contamos con un proceso eficiente para determinar el ancho de un poset y una partición mínima en cadenas. Para las órdenes de intervalo, efectivamente hay una manera sencilla de encontrar ambos. La explicación es solo para establecer una conexión con la coloración de las gráficas de intervalos como se discute en el Capítulo 5.
Dejar\(\textbf{P}=(X,P)\) ser un orden de intervalo y dejar que\(\{[a_x,b_x]:x \in X\}\) sean intervalos de la línea real para que\(x<y\) en\(\textbf{P}\) si y solo\(b_x<a_y\). Entonces deja\(\textbf{G}\) ser la gráfica de intervalos determinada por esta familia de intervalos. Tenga en cuenta que si\(x\) y\(y\) son elementos distintos de\(X\), entonces\(x\) y\(y\) son incomparables en\(\textbf{P}\) si y solo si\(xy\) es un borde en\(\textbf{G}\). En otras palabras,\(\textbf{G}\) es solo la gráfica de incomparabilidad de\(\textbf{P}\).
Recordemos del Capítulo 5 que las gráficas de intervalos son perfectas, es decir,\(\chi(\textbf{G})=ω(\textbf{G})\) para cada gráfica de intervalos\(\textbf{G}\). Además, puede encontrar una coloración óptima de un gráfico de intervalos aplicando el primer ajuste a los vértices en un orden lineal que respete los puntos finales izquierdos. Tal coloración determina simultáneamente una partición de\(\textbf{P}\) en cadenas.
De hecho, si desea omitir la parte sobre las representaciones de intervalo, tome cualquier orden lineal de los elementos como\(x_1, x_2,…,x_n\) para que\(i<j\) siempre\(D(x)\) sea un subconjunto adecuado de\(D(y)\). Luego aplica First Fit con respecto a las cadenas. Por ejemplo, usando el orden de intervalo de 10 puntos ilustrado en la Figura 6.31, aquí hay tal etiquetado:
\(x_1=g\)\(x_2=f\)\(x_3=c\)\(x_4=d\)\(x_5=h\)
\(x_6=a\)\(x_7=j\)\(x_8=b\)\(x_9=i\)\(x_{10}=e\)
Ahora aplica el algoritmo First Fit a los puntos de\(\textbf{P}\), en este orden, para asignarlos a cadenas\(C_1, C_2,….\) En otras palabras, asignar\(x_1\) a cadena\(C_1\). A partir de entonces si ha asignado puntos\(x_1, x_2,…,x_i\) a cadenas, luego asigne\(x_{i+1}\) a cadena\(C_j\) donde\(j\) está el número entero menos positivo para el cual\(x_{i+1}\) es comparable a\(x_k\) siempre\(1 \leq k \leq i\) y ya se le\(x_k\) ha asignado\(C_j\). Por ejemplo, esta regla da como resultado las siguientes cadenas para el orden de intervalo\(\textbf{P}\) mostrado en la Figura 6.31.
\(C_1 = \{g,h,b\}\)
\(C_2 = \{f,a,e\}\)
\(C_3 = \{c,d\}\)
\(C_4 = \{j\}\)
\(C_5 = \{i\}\)
En este caso, es fácil ver que el tabique de cadena es óptimo ya que el ancho de\(\textbf{P}\) es de 5 y\(A=\{a,b,d,i,j\}\) es un anticadena de 5 elementos.
Sin embargo, debe tener mucho cuidado al aplicar First Fit para encontrar tabiques de cadena óptimos, así como uno debe tener cuidado de usar First Fit para encontrar los colores óptimos de las gráficas.
El poset del lado izquierdo de la Figura 6.33 es un poset de altura 2 en 10 puntos, y si el poset se divide en anticadena aplicando First Fit y considerando los puntos en el orden de sus etiquetas, entonces se utilizarán 5 anticadena. ¿Ves cómo extender este poset para obligar a First Fit a usar arbitrariamente muchas anticadena, manteniendo la altura del poset en 2?
En el lado derecho, mostramos un poset de ancho 2. Ahora bien, si este poset se divide en cadenas aplicando First Fit y considerando los puntos en el orden de sus etiquetas, entonces se utilizarán 4 cadenas. ¿Ves cómo extender este poset para forzar a First Fit a usar arbitrariamente muchas cadenas manteniendo el ancho del poset en 2?
¿Tienes la sensación de por qué el segundo problema es un poco más difícil que el primero?
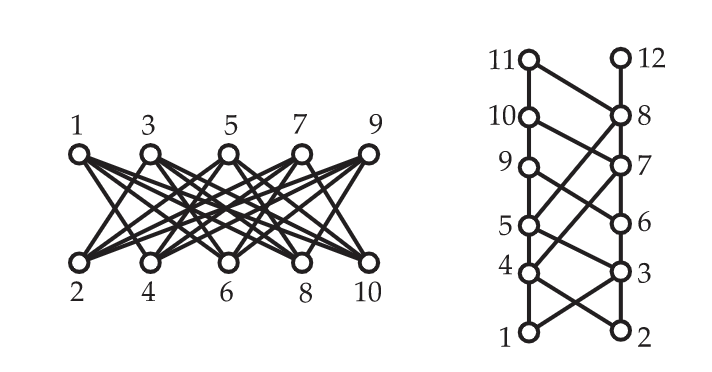
En general, siempre hay algún orden lineal en el conjunto de suelo de un poset para el cual First Fit encontrará una partición óptima en anticadenas. Además, existe un orden lineal (en general diferente al primero) en el conjunto de suelo para el cual First Fit encontrará una partición óptima en cadenas. Sin embargo, no hay ventaja en la búsqueda de tales órdenes, ya que los algoritmos que desarrollamos para encontrar particiones anticadena y cadena óptimas funcionan bastante bien.


