6.7: Encontrar una representación de un orden de intervalo

En esta sección, desarrollamos un algoritmo para encontrar una representación de intervalo de un orden de intervalo. De hecho, este algoritmo se puede aplicar a cualquier poset. O encontrará una representación de intervalo o encontrará un subposet isomórfico a 2+2. Como consecuencia, establecemos la otra mitad del Teorema de Fishburn.

Cuando\(P=(X,P)\) es un orden de intervalo y\(n\) es un entero positivo, puede haber muchas formas diferentes de representar\(\textbf{P}\) usando intervalos con puntos finales enteros en\([n]\). Pero ciertamente hay un mínimo\(n\) para el que se puede encontrar una representación, y aquí vemos que la representación es única. La discusión volverá a hacer uso de la notación para conjuntos descendentes y conjuntos ascendentes que introdujimos antes de la prueba del Teorema de Dilworth. Como recordatorio, lo repetimos aquí. Para un poset\(P=(X,P)\) y un subconjunto\(S \subset X\), let\(D(S)=\{y \in X\): there exists some\(x \in S\) with\(y<x\) in\(P\)}. También, vamos\(D[S]=D(S) \cup S\). Cuando\(|S|=1\), digamos\(S=\{x\}\), escribimos\(D(x)\) y\(D[x]\) más bien que\(D(\{x\})\) y\(D[\{x\}]\). Dualmente, para un subconjunto\(S \subseteq X\), definimos\(U(S)=\{y \in X\): existe algunos\(x \in X\) con\(y>x\) in\(P\)}. Como antes, set\(U[S]=U(S) \cup S\). Y cuando\(S=\{x\}\), solo escribimos\(U(x)\) para\(\{y \in X:x<y\) en\(P\)}.

\(P=(X,P)\)Déjese ser un poset. Comenzamos nuestro procedimiento encontrando los siguientes subconjuntos del conjunto de suelo:\(D=\{D(x):x \in X\}\). Luego distinguimos dos casos. En el primer caso, hay elementos distintos\(x\) y\(y\) para los cuales\(D(x) \nsubseteq D(y)\) y\(D(y) \nsubseteq D(x)\). En este caso, elegimos un elemento\(z \in D(x)−D(y)\) y un elemento\(w \in D(y)−D(x)\). De ello se deduce que los cuatro elementos en {\(x,y,z,w\)} forman un citatorio del\(P\) cual es isomórfico a 2+2.

Nuestro segundo caso es ese\(D(x) \subseteq D(y)\) o\(D(y) \subseteq D(x)\) para todos\(x,y \in X\). En este caso, mostraremos que\(\textbf{P}\) es un orden de intervalo. Ahora encuentra a la familia:\(\mathcal{U}=\{U(x):x \in X\}\). En este caso, es fácil ver que siempre vamos a tener cualquiera\(U(x) \subseteq U(y)\) o\(U(y) \subseteq U(x)\) para todos\(x,y \in X\).

Vamos\(d=|\mathcal{D}|\). En los ejercicios, proporcionaremos (en realidad al hacer tu tarea, proporcionarás) los detalles para respaldar la siguiente declaración:\(|\mathcal{U}|=|\mathcal{D}|\), así que por ahora asumimos que esta afirmación es válida. Etiquetar los conjuntos en\(\mathcal{D}\) y\(\mathcal{U}\) respectivamente como\(D_1, D_2,…,D_d\) y de\(U_1, U_2,…,U_d\) manera que

\(\emptyset = D_1 \subset D_2 \subset D_3 \subset \cdot \cdot \cdot \subset D_d\)y

\(U_1 \supset U_2 \cdot \cdot \cdot \supset U_{d-2} \supset U_{d-1} \supset \cdot \cdot \cdot \supset U_d = \emptyset\).

Formamos una representación\(I\) de intervalo de\(\textbf{P}\) por la siguiente regla: Para cada\(x \in X\), conjunto\(I(x)=[i,j]\), dónde\(D(x)=D_i\) y\(U(x)=U_j\). No queda claro de inmediato que esta regla sea legal, es decir, podría suceder que la aplicación de la regla dé como resultado valores de\(i\) y\(j\) para los cuales\(j<i\). Pero nuevamente, como resultado de los ejercicios, veremos que esto nunca sucede. Esta colección de ejercicios se resume en el siguiente teorema.

Teorema 6.30.

Si\(\textbf{P}\) es un poset excluyendo 2+2, entonces se mantienen las siguientes declaraciones.

1. El número de conjuntos descendentes es igual al número de conjuntos ascendentes. Es decir,\(|\mathcal{D}|=|\mathcal{U}|\).
2. Para cada uno\(x \in X\) , si\(I(x)=[i,j]\) , entonces\(i \leq j\) adentro\(\mathbb{R}\) .
3. Para cada uno\(x,y \in X\) , si\(I(x)=[i,j]\) y\(I(y)=[k,l]\) , entonces\(x<y\) en\(P\) si y solo si\(j<k\) en \(\mathbb{R}\).
4. El entero\(d\) es el número entero menos positivo para el cual\(\textbf{P}\) tiene una representación de intervalo usando los puntos finales enteros de\([d]\) . Esta representación es única.

Considera el poset que se muestra en la Figura 6.31.

Figura 6.31. Un orden de intervalo en 10 Puntos

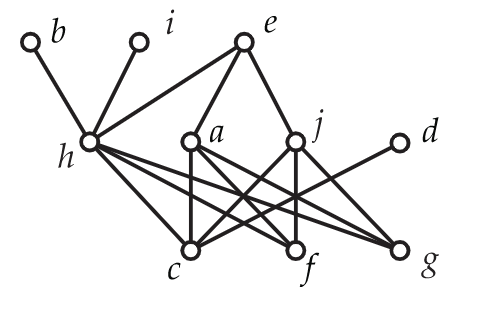
Luego\(d=5\) con\(D_1= \emptyset\),\(D_2=\{c\}\),\(D_3=\{c,f,g\}\),\(D_4=\{c,f,g,h\}\), y\(D_5=\{a,c,f,g,h,j\}\). También\(U_1=\{a,b,d,e,h,i,j\}\),\(U_2=\{a,b,e,h,i,j\}\),\(U_3=\{b,e,i\}\),\(U_4=\{e\}\), y\(U_5= \emptyset\). Entonces

\(I(a)=[3,4]\)\(I(b)=[4,5]\)\(I(c)=[1,1]\)\(I(d)=[2,5]\)\(I(e)=[5,5]\)

\(I(f)=[1,2]\)\(I(g)=[1,2]\)\(I(h)=[3,3]\)\(I(i)=[4,5]\)\(I(j)=[3,4]\)

Para ilustrar la situación en la que este proceso puede ser utilizado para determinar cuándo un poset no es un orden de intervalos, considere nuevamente el poset mostrado en la Figura 6.31. Borre los puntos de unión de línea\(c\) y\(j\). Para el poset resultante, entonces encontrarás eso\(D(j)=\{f,g\}\) y\(D(d)=\{c\}\). Por lo tanto, los cuatro puntos\(c, d, f\) y\(j\) forman una copia de 2+2 en este poset modificado.