9.7: Resolviendo una recurrencia no lineal
- Page ID
- 118554
En esta sección, usaremos funciones generadoras para enumerar el cierto tipo de árboles. Al hacer esto, veremos cómo se pueden usar funciones generadoras para resolver una ecuación de recurrencia no lineal. También haremos una conexión con una secuencia de conteo que encontramos en el Capítulo 2. Para hacer todo esto, debemos introducir un poco de terminología. Un árbol está enraizado si hemos designado un vértice especial llamado su raíz. Siempre dibujaremos nuestros árboles con la raíz en la parte superior y todos los demás vértices debajo de ella. Un árbol sin etiquetar es aquel en el que no hacemos distinciones basadas en nombres dados a los vértices. Para nuestros propósitos, un árbol binario es aquel en el que cada vértice tiene 0 o 2 hijos, y un árbol ordenado es aquel en el que los hijos de un vértice tienen algún orden (primero, segundo, tercero, etc.). Ya que nos centraremos en árboles enraizados, sin etiquetar, binarios, ordenados (RuBots para abreviar), llamaremos a los dos hijos de vértices que tienen hijos los hijos izquierdo y derecho.
En la Figura 9.26, se muestran los árboles enraizados, sin etiquetar, binarios, ordenados con\(n\) hojas para\(n \leq 4\).
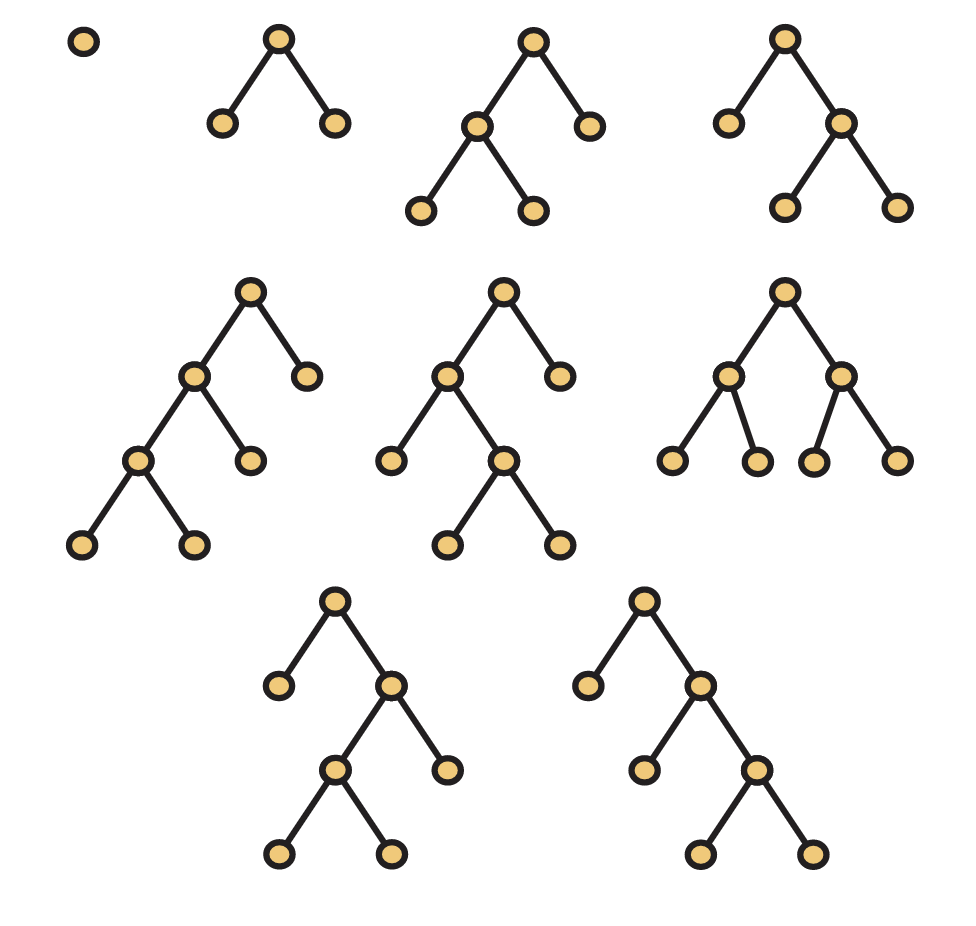
Dejar\(C(x) = \sum_{n=0}^{\infty} c_nx^n\) ser la función generadora para la secuencia\(\{c_n:n \geq 0\}\) donde\(c_n\) está el número de ruBots con\(n\) hojas. (Tomamos\(c_0=0\) por conveniencia.) Entonces podemos ver en la Figura 9.26 eso\(C(x)=x+x^2+2x^3+5x^4+ \cdot \cdot \cdot\). Pero, ¿cuáles son los coeficientes restantes? Veamos cómo podemos romper un RUBOT con\(n\) hojas abajo en una combinación de dos RuBots más pequeños para ver si podemos expresarnos\(c_n\) en términos de algunos\(c_k\) para\(k<n\). Cuando miramos a un RUBOT con\(n \geq 2\) hojas, notamos que el vértice raíz debe tener dos hijos. Esos niños pueden ser vistos como nodos raíz de RUBOT más pequeños, digamos que el niño izquierdo enraiza un RUBOT con\(k\) hojas, es decir, que el niño derecho enraiza un RUBOT con\(n−k\) hojas. Dado que hay\(c_k\) posibles sub-rubots para el niño izquierdo y\(c_{n−k}\) sub-rubots para el hijo derecho, hay un total de\(c_kc_{n−k}\) Rubots en los que el hijo izquierdo de la raíz tiene\(k\) hojas en su sub-rubot. Podemos hacer esto para cualquiera\(k=1,2,…,n−1\), dándonos eso
\(c_n = \displaystyle \sum_{k=1}^{n-1} c_k c_{n-k}\).
(Esto es válido desde\(n \geq 2\).) Ya que\(c_0=0\), en realidad podemos escribir esto como
\(c_n = \displaystyle \sum_{k=0}^n c_k c_{n-k}\).
Veamos el cuadrado de la función generadora\(C(x)\). Por la Proposición 8.3, tenemos
\(C^2(x) = c_0^2 + (c_0c_1 + c_1c_0)x + (c_0c_2 + c_1c_1 + c_2c_0)x^2 + \cdot \cdot \cdot\)
\(= 0 + 0 + (c_0c_2 + c_1c_1 + c_2c_0)x^2 + (c_0c_3 + c_1c_2 + c_2c_1 + c_3c_0)x^3 + \cdot \cdot \cdot\)
Pero ahora vemos de nuestra recursión anterior que el coeficiente on\(x^n\) in no\(C^2(x)\) es más que\(c_n\) para\(n \geq 2\). Todo lo que nos falta es el\(x\) término, así que agregarlo en nos da que
\(C(x) = x + C^2(x)\).
Ahora bien, esta es una ecuación cuadrática en\(C(x)\), así podemos resolver\(C(x)\) y tener
\(C(x) = \dfrac{1 \pm \sqrt{1-4x}}{2} = \dfrac{1 \pm (1-4x)^{1/2}}{2}\).
De ahí que podamos usar el Teorema Binomial de Newton para expandirnos\(C(x)\). Para ello, utilizamos el siguiente lema. Su prueba es casi idéntica a la de Lemma 8.12, y así se omite.
Para cada uno\(k \geq 1\),
\(\dbinom{1/2}{k} = \dfrac{(-1)^{k-1}}{k} \dfrac{\binom{2k-2}{k-1}}{2^{2k-1}}\).
Ahora vemos que
\(C(x) = \dfrac{1}{2} \pm \dfrac{1}{2} \displaystyle \sum_{n=0}^{\infty} \dbinom{1/2}{n} (-4)^nx^n = \dfrac{1}{2} \pm \dfrac{1}{2} (1 + \sum_{n=1}^{\infty} \dfrac{(-1)^{n-1}}{n} \dfrac{\binom{2n-2}{n-1}}{2^{2n-1}} (-4)^nx^n)\)
\( = \dfrac{1}{2} \pm \dfrac{1}{2} \pm \displaystyle \sum_{n=1}^{\infty} \dfrac{\binom{2n-2}{n-1}}{n} x^n\).
Ya que necesitamos\(c_n \geq 0\), tomamos la opción “menos” de la “más o menos” en la fórmula cuadrática y así tenemos el siguiente teorema.
La función generadora para el número\(c_n\) de árboles enraizados, sin etiquetar, binarios y ordenados con\(n\) hojas es
\(C(x) = \dfrac{1- \sqrt{1-4x}}{2} = \displaystyle \sum_{n=1}^{\infty} \dfrac{1}{n} \dbinom{2n-2}{n-1}x^n\).
Observe que\(c_n\) es un número catalán, que encontramos por primera vez en el Capítulo 2, donde estábamos contando caminos de celosía que no cruzaban la línea diagonal\(y=x\). (El coeficiente\(c_n\) es el número catalán que llamamos\(C(n−1)\) en el Capítulo 2.)


