10.1: Una introducción a la probabilidad
- Page ID
- 118474
Continuamos con una discusión informal destinada a motivar el desarrollo más estructurado que seguirá. Considera el “spinner” que se muestra en la Figura 10.1. Supongamos que le damos un buen thwack para que la flecha dé vueltas y vueltas. Después registramos el número de la región en la que el puntero llega a descansar. Entonces los observadores, ninguno de los cuales ha estudiado combinatoria, podrían hacer los siguientes comentarios:
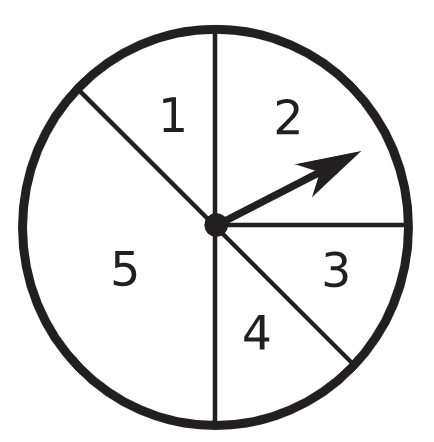
- Las probabilidades de aterrizaje en la región 1 son las mismas que las de aterrizar en la región 3.
- Tienes el doble de probabilidades de aterrizar en la región 2 que en la región 4.
- Cuando aterrizas en una región impar, entonces el 60% del tiempo, será en la región 5.
Ahora desarrollaremos un marco más formal que nos permita hacer este tipo de discusiones mucho más precisas. También veremos si Alice está siendo completamente justa con Bob en su juego propuesto a cien.
Comenzamos definiendo un espacio de probabilidad como un par\((S,P)\) donde\(S\) es un conjunto finito y\(P\) es una función que cuyo dominio es la familia de todos los subconjuntos de\(S\) y cuyo rango es el conjunto [0,1] de todos los números reales que son no negativos y en la mayoría de uno. Además, se deben cumplir las siguientes dos propiedades clave:
- \(P(\emptyset) = 0\)y\(P(S) = 1\).
- Si\(A\) y\(B\) son subconjuntos de\(S\), y\(A \cap B= \emptyset\), entonces\(P(A \cup B) = P(A) + P(B)\).
Cuando\((S,P)\) es un espacio de probabilidad, la función\(P\) se denomina medida de probabilidad, los subconjuntos de\(S\) se llaman eventos, y cuando\(E⊆S\), la cantidad\(P(E)\) se conoce como la probabilidad del evento\(E\).
Tenga en cuenta que podemos considerar\(P\) que se extiende a un mapeo de\(S\) a [0,1] configurando\(P(x)=P(\{x\})\) para cada elemento\(x \in S\). Llamamos a los elementos de\(S\) resultados (algunas personas prefieren decir que los elementos son resultados elementales) y a la cantidad\(P(x)\) se le llama probabilidad de\(x\). Es importante darse cuenta de que si conoces\(P(x)\) para cada uno\(x \in S\), entonces puedes calcular\(P(E)\) para cualquier evento\(E\), ya que (por la segunda propiedad),\(P(E) = \sum_{x \in X} P(x)\).
Para el spinner, podemos tomar\(S=\{1,2,3,4,5\}\), con\(P(1)=P(3)=P(4)=1/8, P(2)=2/8=1/4\) y\(P(5)=3/8\). Entonces\(P(\{2,3\}) = 1/8 + 2/8 = 3/8\).
Dejar\(S\) ser un conjunto finito, no vacío y dejar\(n=|S|\). Para cada uno\(E⊆S\), set\(P(E)=|E|/n\). En particular,\(P(x)=1/n\) para cada elemento\(x \in S\). En este ejemplo trivial, todos los resultados son igualmente probables.
Si se enrolla un solo troquel de seis lados y se registra el número de puntos en la cara superior, entonces el conjunto de tierra es\(S=\{1,2,3,4,5,6\}\) y\(P(i)=1/6\) para cada uno\(i \in S\). Por otro lado, si se tira un par de dados y se registra la suma de los puntos en las dos caras superiores, entonces\(S=\{2,3,4,…,11,12\}\) con\(P(2)=P(12)=1/36, P(3)=P(11)=2/36, P(4)=P(10)=3/36, P(5)=P(9)=4/36, P(6)=P(8)=5/36\) y\(P(7)=6/36\). Para ver esto, considera que los dos mueren como distinguidos, uno muere rojo y el otro azul. Entonces cada uno de los pares\((i,j)\) con\(1 \leq i,j \leq 6\), el dado rojo mostrando\(i\) manchas y el dado azul mostrando\(j\) manchas es igualmente probable. Entonces cada uno tiene probabilidad 1/36. Entonces, por ejemplo, hay tres pares que arrojan un total de cuatro, a saber (3,1), (2,2) y (1,3). Entonces la probabilidad de rodar un cuatro es 3/36=1/12.
En el juego de Alice como se describió anteriormente, el conjunto\(S\) puede ser {0,1,2,3,4,5}, el conjunto de posibles diferencias cuando se tira un par de dados. En este juego, veremos que se\(P\) establecerá la definición correcta de la función\(P(0)=6/36; P(1)=10/36; P(2)=8/36; P(3)=6/36; P(4)=4/36\); y\(P(5)=2/36\). Usando la notación más compacta de Xing, podríamos decir eso\(P(0)=1/6\) y\(P(d)=2(6−d)/36\) cuándo\(d > 0\).
Un frasco contiene veinte canicas, de las cuales seis son rojas, nueve son azules y las cinco restantes son verdes. Tres de las veinte canicas se seleccionan al azar. Dejar\(X=\{0,1,2,3,4,5\}\), y para cada uno\(x \in X\), dejar\(P(x)\) denotar la probabilidad de que sea el número de canicas azules entre las tres canicas seleccionadas\(x\). Entonces\(P(i)=C(9,i)C(11,3−i)/C(20,3)\) por\(i=0,1,2,3\), mientras\(P(4)=P(5)=0\). Bob dice que no tiene sentido tener resultados con probabilidad cero, pero Carlos dice que sí.
En algunos juegos de cartas, cada jugador recibe cinco cartas de una baraja estándar de 52 cartas: cuatro palos (espadas, corazones, diamantes y palos) con 13 cartas, as aunque rey en cada palo. Un jugador tiene una casa llena si hay dos valores\(x\) y\(y\) para los cuales tiene tres de los cuatro\(x\) y dos de los cuatro\(y\), por ejemplo tres reyes y dos ochos. Si se extraen cinco cartas al azar de una baraja estándar, la probabilidad de una casa llena es
\(\dfrac{\binom{13}{1} \binom{12}{1} \binom{4}{3} \binom{4}{2}}{\binom{52}{5}} \approx 0.00144\)


