14.3: Partición en cadena
- Page ID
- 118390
En el capítulo 6, discutimos el teorema de Dilworth, que nos decía que para cualquier poset\(\textbf{P}\) de ancho\(w\), hay una partición de\(\textbf{P}\) en\(w\), pero no menos, cadenas. Sin embargo, solo pudimos idear un algoritmo para encontrar esta partición en cadena (y una anticadena máxima) en el caso especial donde\(\textbf{P}\) se encontraba un orden de intervalo. Ahora, a través de la magia de los flujos de red, podremos idear un algoritmo eficiente que funcione en general para todos los posets. No obstante, para ello requeriremos una red un poco más complicada de lo que ideamos en el apartado anterior.
Supongamos que los puntos de nuestro poset\(\textbf{P}\) son\(\{x_1,x_2,…,x_n\}\). Construimos una red a\(\textbf{P}\) partir de la fuente\(S\), sumidero\(T\), y dos puntos\(x_i′\) y\(x_i″\) para cada punto\(x_i\) de\(\textbf{P}\). Todos los bordes en nuestra red tendrán capacidad 1. Agregamos bordes de\(S\) a\(x_i′\) para\(1≤i≤n\) y de\(x_i″\) a\(T\) para\(1≤i≤n\). Por supuesto, esta red no sería demasiado útil, ya que no tiene bordes desde los nodos de prima única hasta los nodos de doble primo. Para resolver esto, agregamos un borde dirigido de\(x_i′\) a\(x_j″\) si y solo si\(x_i<x_j\) en\(\textbf{P}\).
Nuestro ejemplo de ejecución en esta sección será el poset en la Figura 14.8. a). Discutiremos los puntos del poset como\(x_i\) dónde\(i\) se imprime el número junto al punto en el diagrama.
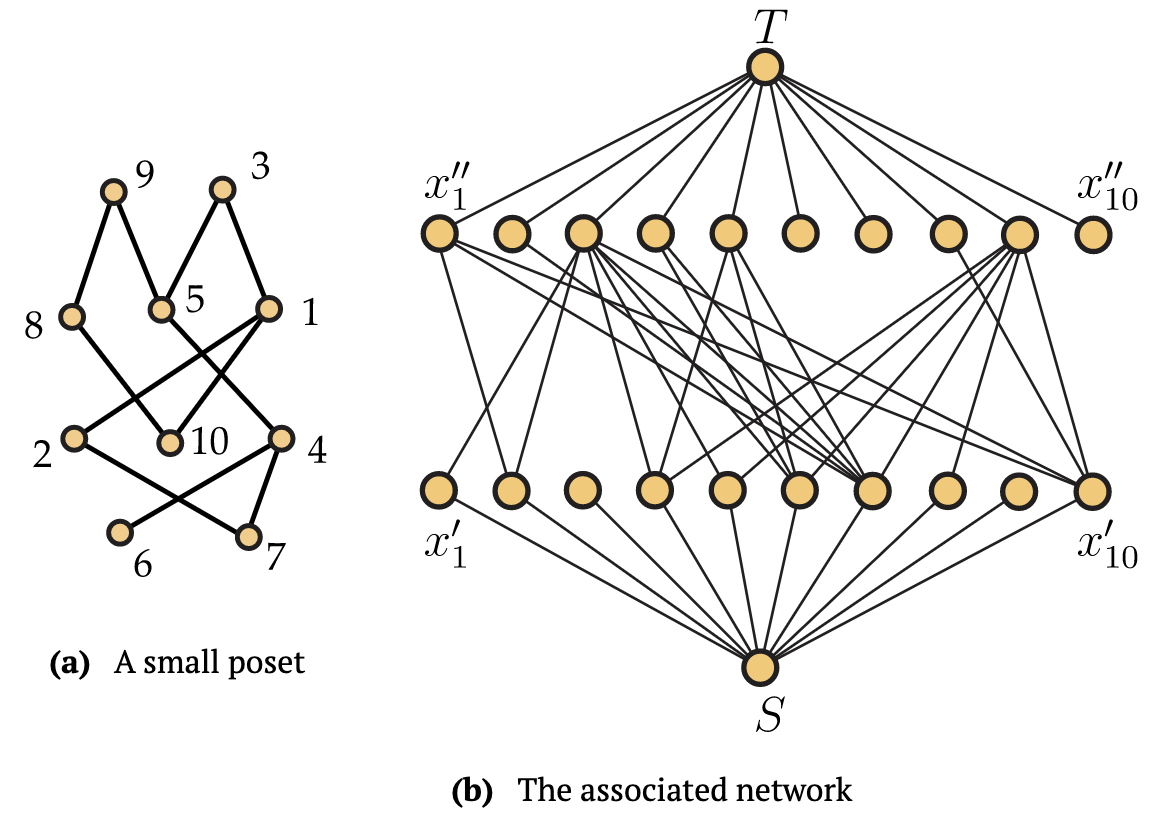
El primer paso es crear la red, la cual mostramos en la Figura 14.8. b). En esta red, todas las capacidades son 1, los bordes se dirigen de abajo hacia arriba, la primera fila de diez vértices es la\(x_i′\) dispuesta consecutivamente con\(x_1′\) a la izquierda y\(x_{10}′\) a la derecha, y la segunda fila de diez vértices es la\(x_i″\) en orden creciente de índice. Para ver cómo se construye esta red, observe que\(x_1<x_3\) en el poset, así tenemos el borde dirigido\((x_1′,x_3″)\). De igual manera,\(x_4\) es menor que\(x_3, x_5\), y\(x_9\) en el poset, lo que lleva a tres bordes dirigidos que salen\(x_4′\) en la red. Como tercer ejemplo, ya que\(x_9\) es máximo en el poset, no hay bordes dirigidos saliendo\(x_9′\).
Todavía no hemos visto cómo podríamos convertir un flujo máximo (o corte mínimo) en la red que acabamos de construir en una partición de cadena mínima o una anticadena máxima. Será más fácil ver cómo funciona esto una vez que tengamos un flujo máximo confirmado. En lugar de ejecutar el algoritmo de etiquetado a partir del flujo cero, observamos un flujo, como el que se muestra en la Figura 14.9. (Nuevamente, usamos la convención de que los bordes gruesos están llenos, mientras que los bordes delgados están vacíos).
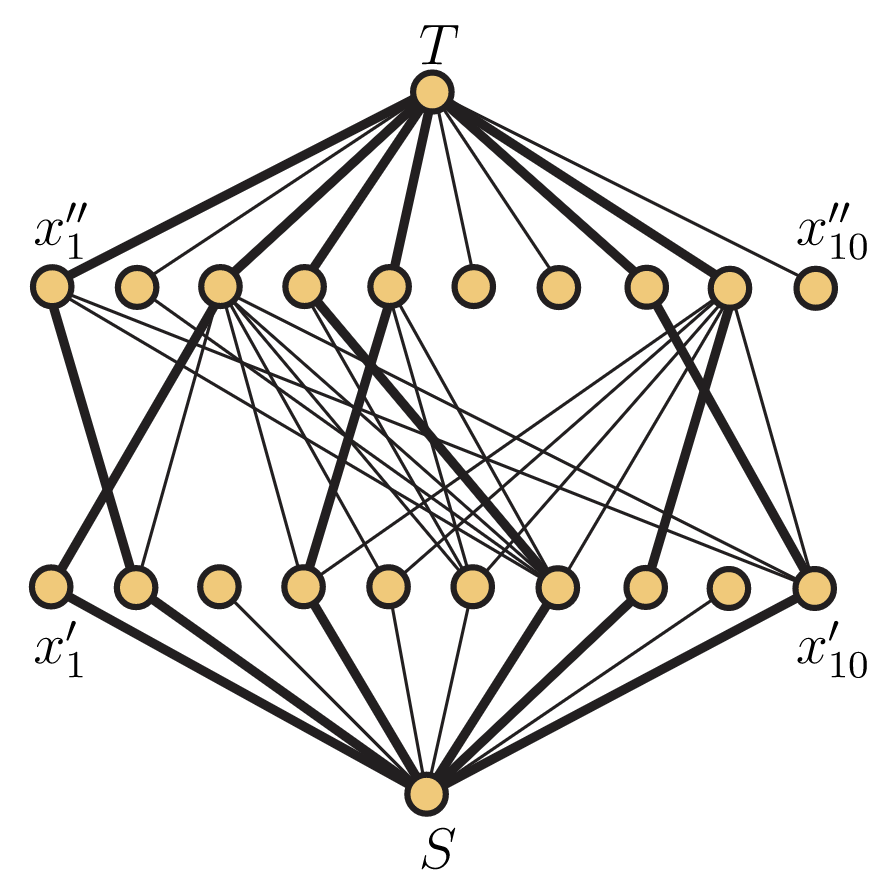
Cuando ejecutamos el algoritmo de etiquetado (usando prioridad\(S,T,x_1′,…,x_{10}′,x_1″,…,x_{10}″)\), obtenemos la siguiente lista de etiquetas:
\(S:(∗,+,∞)\)\(x_9″:(x_5′,+,1)\)\(x_3′:(S,+,1)\)
\(x_3′:(S,+,1)\)\(x_4″:(x_6′,+,1)\)\(x_1″:(x_7′,+,1)\)
\(x_5′:(S,+,1)\)\(x_5″:(x_6′,+,1)\)\(x_2″:(x_7′,+,1)\)
\(x_6′:(S,+,1)\)\(x_1′:(x_3″,−,1)\)\(x_2′:(x_7′,+,1)\)
\(x_9′:(S,+,1)\)\(x_8′:(x_9″,−,1)\)\(T:(x_2″,+,1)\)
\(x_3″:(x_5′,+,1)\)\(x_7′:(x_4″,−,1)\)
Así, encontramos la ruta de aumento\((S,x_6′,x_4″,x_7′,x_2″,T)\), y el flujo actualizado se puede ver en la Figura 14.10.
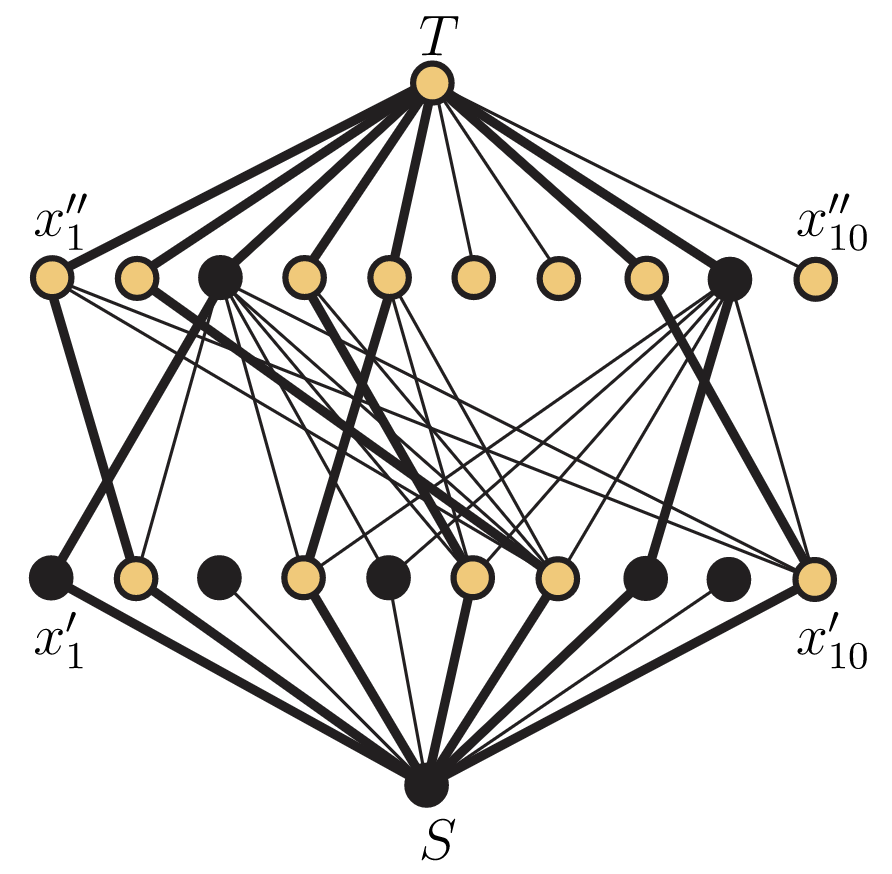
Si volvemos a ejecutar el algoritmo de etiquetado, el algoritmo asigna las etiquetas a continuación, dejando el sumidero sin etiquetar.
\(S:(∗,+,∞)\)\(x_5′:(S,+,1)\)\(x_3″:(x_5′,+,1)\)\(x_1′:(x_3″,−,1)\)
\(x_3′:(S,+,1)\)\(x_9′:(S,+,1)\)\(x_9″:(x_5′,+,1)\)\(x_8′:(x_9″,−,1)\)
En la Figura 14.10, los vértices negros son aquellos que están etiquetados en la pasada final, mientras que los vértices dorados son los vértices no etiquetados.
Ahora que ya hemos repasado la parte que ya sabías hacer, necesitamos discutir cómo traducir este flujo de red y cortar en una partición de cadena y una anticadena. Si hay una unidad de flujo en un borde\((x_i′,x_j″)\), entonces un buen primer instinto es colocar\(x_i\) y\(x_j\) en la misma cadena de una partición de cadena. Para poder hacer esto con éxito, por supuesto, necesitamos asegurarnos de que esto no resulte en que dos puntos incomparables se coloquen en una cadena. Una manera de ver que todo funciona como se desea es pensar en empezar\((x_i′,x_j″)\) y luego buscar flujo saliendo\(x_j′\). Si la hay, va a un vértice\(x_k″\), por lo que podemos agregar xk a la cadena ya que\(x_i<x_j<x_k\). Continuar de esta manera hasta llegar a un vértice en la red que no tenga ningún flujo saliendo de ella. Entonces a ver si\(x_i″\) tiene flujo entrando en él. Si lo hace, es a partir de un vértice\(x_m′\) que se puede agregar desde entonces\(x_m<x_i<x_j\).
Veamos cómo seguir este proceso para el flujo en la Figura 14.10 conduce a una partición en cadena. Si empezamos con\(x_1′\), vemos que\((x_1′,x_3″)\) está lleno, así que colocamos\(x_1\) y\(x_3\) en cadena\(C_1\). Ya que no\(x_3′\) tiene flujo dejándolo, no hay mayores elementos para agregar a la cadena. Sin embargo,\(x_1″\) tiene flujo desde\(x_2′\), así que agregamos\(x_2\) a\(C_1\). Ahora vemos que\(x_2″\) ha fluir desde\(x_7′\), así que ahora\(C_1=\{x_1,x_2,x_3,x_7\}\). Vertex no\(x_7″\) tiene flujo en él, por lo que la construcción de la primera cadena se detiene. El primer vértice que no hemos colocado en una cadena es\(x_4\), por lo que notamos que\((x_4′,x_5″)\) está lleno, colocando\(x_4\) y\(x_5\) en cadena\(C_2\). Luego miramos desde\(x_5′\) y no vemos salir flujo. Sin embargo, hay flujo de entrada\(x_4″\) de\(x_6′\), por lo que\(x_6\) se agrega a\(C_2\). No hay flujo fuera de\(x_6″\), entonces\(C_2=\{x_4,x_5,x_6\}\). Ahora el primer punto no en una cadena es\(x_8\), así que usamos el flujo de\(x_8′\) a\(x_9″\) a lugar\(x_8\) y\(x_9\) en cadena\(C_3\). Nuevamente, no hay flujo de salida\(x_9′\), así que miramos a\(x_8″\), que está recibiendo flujo de\(x_{10}″\). Sumando\(x_{10}\) a\(C_3\) da\(C_3=\{x_8,x_9,x_{10}\}\), y como cada punto está ahora en una cadena, podemos detenernos.
Incluso una vez que vemos que el proceso anterior de hecho genera una partición en cadena, no está claro de inmediato que se trata de una partición de cadena mínima. Para ello, necesitamos encontrar un anticadena de tantos puntos como cadenas haya en nuestra partición. (En el ejemplo que hemos estado usando, necesitamos encontrar una anticadena de tres elementos). Aquí es donde es útil rastrear los vértices etiquetados. Supongamos que hemos determinado una cadena\(C=\{x_1<x_2< \cdot \cdot \cdot <x_k\}\) usando el flujo de red. Dado que\(x_1\) es el elemento mínimo de esta cadena, no hay flujo de entrada\(x_1″\) y, por lo tanto, no hay flujo de salida\(x_1″\). Dado que no\(T\) está etiquetada, esto debe significar que no\(x_1″\) está etiquetada. Del mismo modo,\(x_k\) es el elemento máximo de\(C\), por lo que no hay flujo de salida de\(x_k′\). Así,\(x_k′\) se etiqueta. Ahora considerando la secuencia de vértices
\(x_k′,x_k″,x_{k−1}′,x_{k−1}″,…,x_2′,x_2″,x_1′,x_1″\),
debe haber un lugar donde los vértices pasen de ser etiquetados a no etiquetados. Esto debe suceder con\(x_i′\) etiquetado y\(x_i″\) sin etiquetar. Para ver por qué, supongamos que\(x_i′\) y ambos\(x_i″\) están sin etiquetar mientras\(x_{i+1}′\) y ambos\(x_{i+1}″\) están etiquetados. Porque\(x_i\) y\(x_{i+1}\) son consecutivos en\(C\), hay flujo en\((x_i′,x_{i+1}″)\). Por lo tanto, al escanear desde\(x_{i+1}″\), se\(x_i′\) etiquetaría el vértice. Para cada cadena de la partición de cadena, luego tomamos el primer elemento\(y\) para el cual\(y′\) está etiquetado y no\(y″\) está etiquetado para formar una anticadena\(A=\{y_1,…,y_w\}\). Para ver que\(A\) es un anticadena, fíjese que si\(y_i<y_j\), entonces\((y_i′,y_j″)\) es un borde en la red. Por lo tanto, el escaneo de\(y_i′\) etiquetaría\(y_j″\). Usando este proceso, encontramos que un máximo anticadena en nuestro ejemplo es\(\{x_1,x_5,x_8\}\).


