14.2: Emparejamientos en Gráficas Bipartitas

Recordemos que una gráfica bipartita\(\textbf{G}=(V,E)\) es aquella en la que los vértices se pueden colorear correctamente usando solo dos colores. Está claro que tal coloración luego se\(V\) divide en dos conjuntos independientes\(V_1\) y\(V_2\), y así todos los bordes están entre\(V_1\) y\(V_2\). Los gráficos bipartitos tienen muchas aplicaciones útiles, particularmente cuando tenemos dos tipos distintos de objetos y una relación que tiene sentido solo entre objetos de distintos tipos. Por ejemplo, supongamos que se tiene un conjunto de trabajadores y un conjunto de trabajos para que los trabajadores hagan. Podemos considerar a los trabajadores como el conjunto\(V_1\) y los trabajos como\(V_2\) y agregar una ventaja de trabajador\(w \in V_1\) a trabajo\(j \in V_2\) si y solo si\(w\) está calificado para hacer\(j\).

Por ejemplo, la gráfica de la Figura 14.2 es una gráfica bipartita en la que hemos dibujado\(V_1\) en la parte inferior y\(V_2\) en la parte superior.

Figura 14.2. Una gráfica bipartita

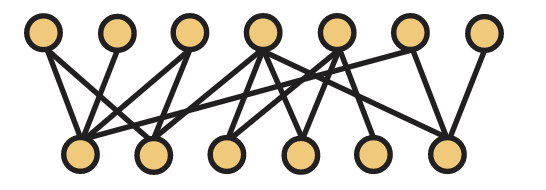
Si\(\textbf{G}=(V,E)\) es una gráfica, un conjunto\(M \subseteq E\) es una coincidencia en\(\textbf{G}\) si no hay dos bordes de\(M\) compartir un punto final. Si\(v\) es un vértice que es el punto final de un borde en\(M\), decimos que\(M\) satura\(v\) o\(v\) está saturado por\(M\). Cuando\(\textbf{G}\) es bipartito con\(V=V_1 \cup V_2\), una coincidencia es entonces una forma de emparejar vértices\(V_1\) con vértices en\(V_2\) para que ningún vértice se empareja con más de otro vértice. Normalmente nos interesa encontrar una coincidencia máxima, que es una coincidencia que contiene el mayor número de aristas posible, y en las gráficas bipartitas solemos fijar los conjuntos\(V_1\)\(V_2\) y buscar una coincidencia máxima de\(V_1\) a\(V_2\). En nuestro ejemplo de trabajadores y empleos, el problema de emparejamiento se convierte así en tratar de encontrar una asignación de trabajadores a trabajos tales que

i. cada trabajador es asignado a un trabajo para el que está calificado (es decir, hay una ventaja),

ii. a cada trabajador se le asigna como máximo un empleo, y

iii. a cada empleo se le asigna como máximo un trabajador.

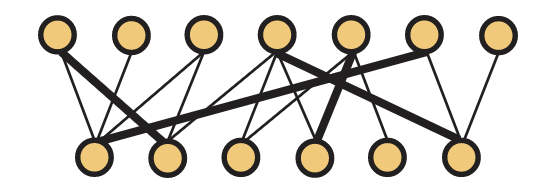
Como ejemplo, en la Figura 14.3, los bordes gruesos forman una coincidencia de\(V_1\) a\(V_2\). Supongamos que eres el encargado de estos trabajadores (en la parte inferior) y debes asignarlos a los trabajos (en la parte superior). ¿De verdad estás haciendo el mejor uso de tus recursos poniendo a trabajar solo a cuatro de seis trabajadores? No hay formas triviales de mejorar el número de trabajadores ocupados, ya que los dos sin responsabilidades en este momento no pueden hacer ninguno de los trabajos que no están asignados. Quizás haya una asignación más eficiente que se pueda hacer rehaciendo algunas de las asignaciones, sin embargo. Si la hay, ¿cómo deberías ir para encontrarla? Si no la hay, ¿cómo le justificarías a tu jefe que no hay mejor asignación de trabajadores a trabajos?

Figura 14.3. Una coincidencia en una gráfica bipartita

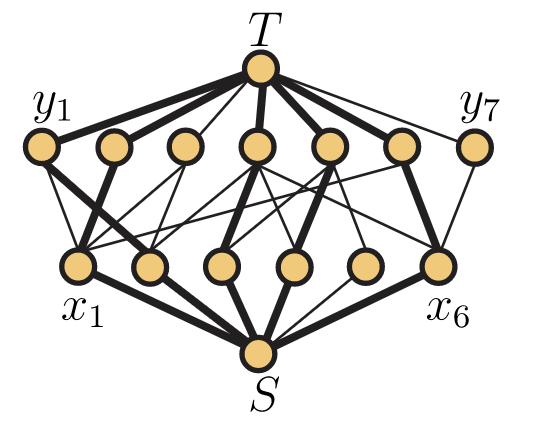
Al final de la sección, veremos brevemente un teorema sobre emparejamientos en gráficas bipartitas que nos dice precisamente cuándo existe una asignación de trabajadores a empleos que asegura que cada trabajador tenga un empleo. Primero, sin embargo, queremos ver cómo se pueden usar los flujos de red para encontrar los máximos emparejamientos en gráficas bipartitas. El algoritmo que damos, aunque decente, no es el algoritmo más eficiente conocido para este problema. Por lo tanto, no es probable que sea el que se utiliza en la práctica. Sin embargo, es un buen ejemplo de cómo se pueden usar los flujos de red para resolver un problema combinatorio. La red que utilizamos se forma a partir de una gráfica bipartita\(\textbf{G}\) colocando un borde desde la fuente\(S\) hasta cada vértice de\(V_1\) y un borde desde cada vértice del\(V_2\) sumidero\(T\). Los bordes entre\(V_1\) y\(V_2\) están orientados de\(V_1\) a\(V_2\), y a cada borde se le da capacidad 1. La Figura 14.4 contiene la red correspondiente a nuestra gráfica de la Figura 14.2. Los bordes en esta red están todos orientados de abajo hacia arriba y todos los bordes tienen capacidad 1. Los vértices en\(V_1\) están\(x_1,…,x_6\) en orden de izquierda a derecha, mientras que los vértices en\(V_2\) son\(y_1,…,y_7\) de izquierda a derecha.

Figura 14.4. La red correspondiente a una gráfica bipartita

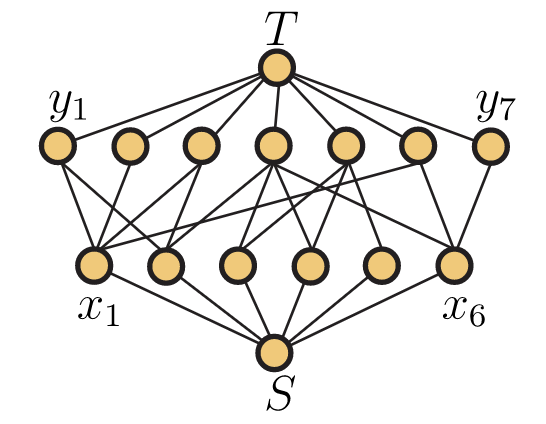
Ahora que hemos traducido una gráfica bipartita a una red, necesitamos abordar la correspondencia entre los emparejamientos y los flujos de red. Para convertir una coincidencia\(M\) en un flujo de red, comenzamos colocando una unidad de flujo en los bordes de la coincidencia. Para tener un flujo válido, también debemos colocar una unidad de flujo en los bordes desde\(S\) hasta los vértices de\(V_1\) saturado por\(M\). Dado que cada uno de estos vértices es incidente con un solo borde de\(M\), el flujo de salida de cada uno de ellos es 1, coincidiendo con el flujo de entrada. De igual manera, el enrutamiento de una unidad de flujo hacia\(T\) desde cada uno de los vértices de\(V_2\) saturado por\(M\) se encarga de las leyes de conservación para los vértices restantes. Para ir en la otra dirección, simplemente tenga en cuenta que los bordes completos de\(V_1\) a\(V_2\) en un flujo de valor entero es una coincidencia. Así, podemos encontrar una coincidencia máxima de\(V_1\) a simplemente\(V_2\) ejecutando el algoritmo de etiquetado en la red asociada para encontrar un flujo máximo.

En la Figura 14.5, mostramos bordes gruesos para mostrar los bordes con flujo 1 en el flujo correspondiente a nuestra suposición a una coincidencia de la Figura 14.3.

Figura 14.5. El flujo correspondiente a una coincidencia

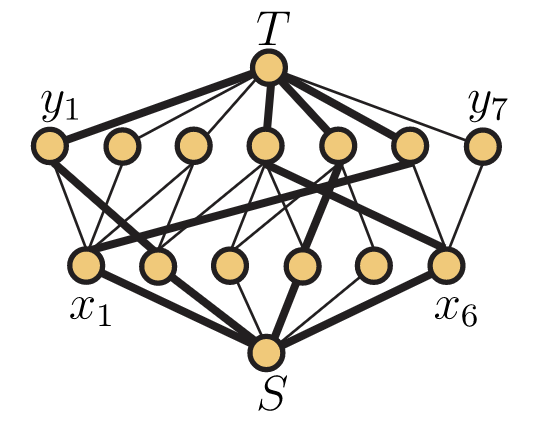
Con la secuencia de prioridad\(S,T,x_1,x_2,…,x_6,y_1,y_2,…,y_7\) reemplazando nuestro orden pseudo-alfabético habitual, el algoritmo de etiquetado produce las etiquetas que se muestran a continuación.

\(S:(∗,+,∞)\)\(y_6:(x_6,+,1)\)

\(x_3:(S,+,1)\)\(x_1:(y_6,−,1)\)

\(x_5:(S,+,1)\)\(y_1:(x_1,+,1)\)

\(y_4:(x_3,+,1)\)\(y_2:(x_1,+,1)\)

\(y_5:(x_3,+,1)\)\(y_3:(x_1,+,1)\)

\(x_6:(y_4,−,1)\)\(x2:(y_1,−,1)\)

\(x4:(y_5,−,1)\)\(T:(y_2,+,1)\)

Esto nos lleva al camino de aumento\(S,x_3,y_4,x_6,y_6,x_1,y_2,T\), que nos da el flujo que se muestra en la Figura 14.6.

Figura 14.6. El flujo incrementado

¿Es este un flujo máximo? Otra ejecución del algoritmo de etiquetado produce

\(S:(∗,+,∞)\)\(x_4:(y_5,−,1)\)

\(x_5:(S,+,1)\)\(y_4:(x_4,+,1)\)

\(y_5:(x_5,+,1)\)\(x_3:(y_4,−,1)\)

y luego se detiene. Así, el flujo en la Figura 14.6 es un flujo máximo.

Ahora que sabemos que tenemos un flujo máximo, nos gustaría poder argumentar que la coincidencia que hemos encontrado también es máxima. Después de todo, el jefe no va a estar contento si más tarde se entera de que este algoritmo de fantasía que afirmaste daba una asignación óptima de trabajos a los trabajadores dejó al quinto trabajador (\(x_5\)) sin empleo cuando los seis podrían haber sido puestos a trabajar. Echemos un vistazo a qué vértices fueron etiquetados por el algoritmo de etiquetado Ford-Fulkerson en la última ejecución. Hubo tres vértices (\(x_3, x_4, and x_5\)) de\(V_1\) etiquetado, mientras que solo hubo dos vértices (\(y_4\)y\(y_5\)) de\(V_2\) etiquetados. Observe que\(y_4\) y\(y_5\) son los únicos vértices que son vecinos de\(x_3, x_4\), o\(x_5\) en\(\textbf{G}\). Así, no importa cómo escojamos los bordes coincidentes\(\{x_3,x_4,x_5\}\), uno de estos vértices quedará insaturado. Por lo tanto, uno de los trabajadores debe ir sin asignación laboral. (En nuestro ejemplo, es el quinto, pero es posible elegir diferentes bordes para el emparejamiento así que otro de ellos se quede sin tarea alguna).

El fenómeno que acabamos de observar no es exclusivo de nuestro ejemplo. De hecho, en cada gráfica bipartita\(\textbf{G}=(V,E)\) con\(V=V_1 \cup V_2\) en la que no podamos encontrar una coincidencia que satura todos los vértices de\(V\), encontraremos una configuración similar. Se trata de un famoso teorema de Hall, que exponemos a continuación.

Teorema 14.7. Teorema de Hall

Deja\(\textbf{G}=(V,E)\) ser una gráfica bipartita con\(V=V_1 \cup V_2\). Hay una coincidencia que satura todos los vértices de\(V_1\) if y solo si por cada subconjunto\(A⊆V_1\), el conjunto\(N⊆V\) de vecinos de los vértices en\(A\) satisface\(|N| \geq |A|\).