1.7: El principio del encasillamiento
- Page ID
- 117122
Un paso clave en muchas pruebas consiste en mostrar que dos valores posiblemente diferentes son de hecho los mismos. El principio de Pigeonhole a veces puede ayudar con esto.
Teorema \(\PageIndex{1}\): Pigeonhole Principle
Supongamos que\(n+1\) (o más) objetos se ponen en\(n\) cajas. Entonces alguna caja contiene al menos dos objetos.
- Prueba
-
Supongamos que cada caja contiene como máximo un objeto. Entonces el número total de objetos es a lo sumo\(1+1+\cdots+1=n\), una contradicción.
Este hecho aparentemente simple se puede utilizar de formas sorprendentes. La clave suele ser poner objetos en cajas de acuerdo con alguna regla, de manera que cuando dos objetos terminan en la misma caja es porque tienen alguna relación deseada.
Ejemplo\(\PageIndex{1}\):
Entre 13 personas cualquiera, al menos dos comparten un mes de nacimiento.
Etiqueta 12 cajas con los nombres de los meses. Ponga a cada persona en la caja etiquetada con su mes de nacimiento. Alguna caja contendrá al menos dos personas, que comparten un mes de nacimiento.
Ejemplo\(\PageIndex{2}\):
Supongamos que 5 pares de calcetines están en un cajón. Escogiendo 6 calcetines garantiza que se elija al menos un par.
Etiquetar las cajas por “los pares” (por ejemplo, el par rojo, el par azul, el par argyle,...). Pon los 6 calcetines en las cajas de acuerdo a la descripción.
Algunos usos del principio no son tan sencillos.
Ejemplo\(\PageIndex{3}\)
Supongamos que\(a_1,\ldots,a_n\) son números enteros. Entonces alguna “suma consecutiva”\(a_k+a_{k+1}+a_{k+2}+\cdots+a_{k+m}\) es divisible por\(n\).
Considera estas\(n\) sumas:\[\eqalign{ s_1&=a_1\cr s_2&=a_1+a_2\cr s_3&=a_1+a_2+a_3\cr &\vdots\cr s_n&=a_1+a_2+\cdots+a_n\cr }\nonumber\]
Todas estas son sumas consecutivas, así que si una de ellas es divisible por\(n\) nosotros estamos hechos. Si no, dividir cada uno por\(n\) deja un resto distinto de cero\(r_1=s_1\bmod n\),,\(r_2=s_2\bmod n\), y así sucesivamente. Estos restos tienen valores en\(\{1,2,3,\ldots,n-1\}\). Etiquete\(n-1\) las cajas con estos\(n-1\) valores; ponga cada una de las\(n\) sumas en la caja etiquetada con su resto mod\(n\). Dos sumas terminan en la misma caja, lo que significa que\(s_i\bmod n=s_j\bmod n\) para algunos\(j>i\); de ahí que\(s_j-s_i\) sea divisible por\(n\), y\(s_j-s_i=a_{i+1}+a_{i+2}+\cdots+a_j\), como se desee.
Un argumento similar proporciona una prueba del Teorema del resto chino.
Teorema \(\PageIndex{2}\): Chinese Remainder Theorem
Si\(m\) y\(n\) son relativamente primos, y\(0\le a< m\) y\(0\le b< n\), entonces hay un entero\(x\) tal que\(x\bmod m=a\) y\(x\bmod n=b\).
- Prueba
-
Considera los enteros\(a,a+m,a+2m,\ldots a+(n-1)m\), cada uno con el resto\(a\) cuando se divide por\(m\). Deseamos demostrar que uno de estos enteros tiene resto\(b\) cuando se divide por\(n\), en cuyo caso ese número satisface la propiedad deseada.
Para una contradicción, supongamos que no. Que los restos sean\(r_0=a\bmod n\),\(r_1=a+m\bmod n\),...,\(r_{n-1}=a+(n-1)m\bmod n\). Etiquetar\(n-1\) las cajas con los números\(0,1,2,3,\ldots,b-1,b+1,\ldots n-1\). Poner cada uno\(r_i\) en la caja etiquetada con su valor. Dos restos terminan en la misma caja, digamos\(r_i\) y\(r_j\), con\(j>i\), así\(r_i=r_j=r\). Esto significa que\[a+im=q_1n+r\quad\hbox{and}\quad a+jm=q_2n+r.\nonumber\]
De ahí\[\eqalign{ a+jm-(a+im)&=q_2n+r-(q_1n+r)\cr (j-i)m&=(q_2-q_1)n.\cr }\nonumber\]
Dado que\(n\) es relativamente primo a\(m\), esto significa que\(n | (j-i)\). Pero desde\(i\) y\(j\) están en\(\{0,1,2,\ldots,n-1\}\),\(0< j-i< n\), entonces\(n\cancel{|}(j-i)\). Esta contradicción termina la prueba.
Las versiones más generales del Principio de Pigeonhole se pueden probar esencialmente por el mismo método. Una generalización natural sería algo como esto: Si\(X\) los objetos se ponen en\(n\) cajas, alguna caja contiene al menos\(m\) objetos. Por ejemplo:
Teorema \(\PageIndex{3}\)
Supongamos que\(r_1,\ldots,r_n\) son enteros positivos. Si\(X\ge(\sum_{i=1}^n r_i) -n + 1\) los objetos se colocan en\(n\) cajas etiquetadas\(1,2,3,\ldots,n\), entonces alguna caja etiquetada\(i\) contiene al menos\(r_i\) objetos.
- Prueba
-
Supongamos que no. Entonces el número total de objetos en las cajas es a lo sumo\((r_1-1)+(r_2-1)+(r_3-1)+\cdots+(r_n-1)=(\sum_{i=1}^n r_i) -n < X\), una contradicción.
Esta generalización completa solo es necesaria ocasionalmente; muchas veces esta versión más simple es suficiente:
Corolario \(\PageIndex{1}\)
Supongamos\(r>0\) y\(X\ge n(r-1)+1\) los objetos se colocan en\(n\) cajas. Entonces alguna caja contiene al menos\(r\) objetos.
- Prueba
-
Aplicar el teorema anterior con\(r_i=r\) para todos\(i\).
\[\bullet\quad\bullet\quad\bullet\nonumber\]
Aquí hay una sencilla aplicación del Principio Pigeonhole que lleva a muchas preguntas interesantes.
Ejemplo\(\PageIndex{4}\)
Supongamos que 6 personas están reunidas; entonces o 3 de ellas se conocen mutuamente, o 3 de ellas se desconocen mutuamente.
Convertimos esto en una pregunta de teoría gráfica: Considere la gráfica que consta de 6 vértices, cada uno conectado a todos los demás por un borde, llamado el gráfico completo sobre\(6\) vértices, y denotado\(K_6\); los vértices representan a las personas. Colorea un borde de rojo si las personas representadas por sus puntos finales están familiarizadas, y azul si no están familiarizadas. Cualquier elección de 3 vértices define un triángulo; queremos mostrar que o bien hay un triángulo rojo o un triángulo azul.
Considera los cinco bordes incidentes en un solo vértice\(v\); por el Principio de Agujero Paloma (la versión en corolario 1.6.7, con\(r=3\),\(X=2(3-1)+1=5\)), al menos tres de ellos son del mismo color, lo llaman color\(C\); llaman al otro color\(D\). Que los vértices en los otros extremos de estos tres bordes sean\(v_1\),\(v_2\),\(v_3\). Si alguno de los bordes entre estos vértices tiene color\(C\), hay un triángulo de color\(C\): si el borde se conecta\(v_i\) a\(v_j\), el triángulo está formado por\(v\),\(v_i\), y\(v_j\). Si este no es el caso, entonces los tres vértices\(v_1\),\(v_2\),\(v_3\) se unen por bordes de color\(D\), y forman un triángulo de color\(D\).
El número 6 en este ejemplo es especial: con 5 o menos vértices no es cierto que deba haber un triángulo monocromático, y con más de 6 vértices es cierto. Para ver que no es cierto para 5 vértices, sólo necesitamos mostrar un ejemplo, como en la Figura\(\PageIndex{1}\).
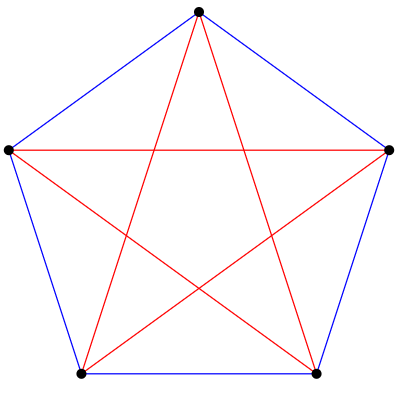
El número Ramsey\(R(i)\) es el entero más pequeño de\(n\) tal manera que cuando los bordes de\(K_n\) están coloreados con dos colores, hay una gráfica completa monocromática sobre\(i\) vértices,\(K_i\), contenida dentro\(K_n\). El ejemplo lo demuestra\(R(3)=6\).
More generally, \(R(i,j)\) is the smallest integer \(n\) such that when the edges of \(K_n\) are colored with two colors, say \(C_1\) and \(C_2\), either there is a \(K_i\) contained within \(K_n\) all of whose edges are color \(C_1\), or there is a \(K_j\) contained within \(K_n\) all of whose edges are color \(C_2\). Using this notion, \(R(k)=R(k,k)\). More generally still, \(R(i_1,i_2,\ldots,i_m)\) is the smallest integer \(n\) such that when the edges of \(K_n\) are colored with \(m\) colors, \(C_1,…,C_m\), then for some \(j\) there is a \(K_{i_j}\) contained in \(K_n\) all of whose edges are color \(C_j\).
Ramsey proved that in all of these cases, there actually is such a number \(n\). Generalizations of this problem have led to the subject called Ramsey Theory.
Computing any particular value \(R(i,j)\) turns out to be quite difficult; Ramsey numbers are known only for a few small values of \(i\) and \(j\), and in some other cases the Ramsey number is bounded by known numbers. Typically in these cases someone has exhibited a \(K_m\) and a coloring of the edges without the existence of a monochromatic \(K_i\) or \(K_j\) of the desired color, showing that \(R(i,j)>m\); and someone has shown that whenever the edges of \(K_n\) have been colored, there is a \(K_i\) or \(K_j\) of the correct color, showing that \(R(i,j)\le n\).


