3.E: Generando Funciones (Ejercicios)

3.2: Teorema del Binomio de Newton

Para algunos de estos ejercicios, es posible que desee utilizar el applet sage anterior, en el Ejemplo 3.2.3, o su sistema de álgebra por computadora favorito.

Ejercicio\(\PageIndex{2.1}\)

Demostrar eso\({r\choose k}={r-1\choose k-1}+{r-1\choose k}\).

Ejercicio\(\PageIndex{2.2}\)

Demuestre que la serie Maclaurin para\((x+1)^r\) es\(\sum_{i=0}^\infty {r\choose i}x^i\).

Ejercicio\(\PageIndex{2.3}\)

En cuanto al Ejemplo 3.2.3, mostrar que todos los coeficientes que comienzan con\(x^{16}\) son 180.

Ejercicio\(\PageIndex{2.4}\)

Utilice una función generadora para encontrar el número de soluciones a\( x_1+x_2+x_3+x_4=14\), dónde\(0\le x_1\le3\),\(2\le x_2\le5\),\(0\le x_3\le5\),\(4\le x_4\le6\).

Ejercicio\(\PageIndex{2.5}\)

Encuentra la función generadora para el número de soluciones a\( x_1+x_2+x_3+x_4=k\), donde\(0\le x_1\le\infty\),\(3\le x_2\le\infty\),\(2\le x_3\le5\),\(1\le x_4\le5\).

Ejercicio\(\PageIndex{2.6}\)

Encuentra una función generadora para el número de soluciones enteras no negativas a\(3x+2y+7z=n\).

Ejercicio\(\PageIndex{2.7}\)

Supongamos que tenemos un gran suministro de globos rojos, blancos y azules. ¿Cuántos racimos diferentes de 10 globos hay, si cada manojo debe tener al menos un globo de cada color y el número de bolas blancas debe ser par?

Ejercicio\(\PageIndex{2.8}\)

Usa funciones generadoras para mostrar que cada entero positivo se puede escribir exactamente de una manera como una suma de distintas potencias de 2.

Ejercicio\(\PageIndex{2.9}\)

Supongamos que tenemos un gran suministro de velas azules y verdes, y una vela dorada. ¿Cuántas colecciones de\(n\) velas hay en las que el número de velas azules es par, el número de velas verdes es cualquier número y el número de velas doradas es como máximo uno?

3.3: Funciones de generación exponencial

Ejercicio\(\PageIndex{3.1}\)

Encuentra el coeficiente de\(x^9/9!\) en la función del Ejemplo 3.3.1. Puedes usar Sage o un programa similar.

# Enter your function here (e^x shown as an example):
f=exp(x)
# Now we compute the first few terms of the Taylor series, 
# extract the coefficients, and multiply by the factorial to
# get the part of the coefficients we want. 
g=f.taylor(x,0,13)
L=g.coefficients()
coeffs={c[1]:c[0]*factorial(c[1]) for c in L}
# coeffs is now a "dictionary" that holds pairs n:m, where
# n is the exponent and m is the coefficient. Note that
# coefficients with value zero are not included.
coeffs

Ejercicio\(\PageIndex{3.2}\)

Encontrar una función generadora exponencial para el número de permutaciones con repetición\(n\) de longitud del conjunto\(\{a,b,c\}\), en la que hay un número impar de\(a\,\) s, un número par de\(b\,\) s, y un número par de\(c\,\) s.

Ejercicio\(\PageIndex{3.3}\)

Encontrar una función generadora exponencial para el número de permutaciones con repetición\(n\) de longitud del conjunto\(\{a,b,c\}\), en la que el número de\(a\,\) s es par y al menos 2, el número de\(b\,\) s es par y como máximo 6, y el número de\(c\,\) s es al menos 3.

Ejercicio\(\PageIndex{3.4}\)

¿De cuántas maneras podemos pintar las 10 habitaciones de un hotel si a lo sumo tres se pueden pintar de rojo, como máximo 2 pintadas de verde, como máximo 1 pintadas de blanco, y cualquier número se puede pintar de azul o naranja?

Ejercicio\(\PageIndex{3.5}\)

Recordemos de la Sección 1.5 que los números de Campana\(B_n\) cuentan todas las particiones de\(\{1,2,\ldots,n\}\).

Dejar\( f(x)=\sum_{n=0}^\infty B_n\cdot {x^n\over n!}\), y señalar que\[ f'(x)=\sum_{n=1}^\infty B_n {x^{n-1}\over (n-1)!}= \sum_{n=0}^\infty B_{n+1}{x^{n}\over n!}= \sum_{n=0}^\infty \left(\sum_{k=0}^n {n\choose k}B_{n-k}\right) {x^{n}\over n!}, \nonumber\] usando la relación de recurrencia Ecuación 1.5.1 para\(B_{n+1}\) de la Sección 1.5. Ahora es posible escribir esto como producto de dos series infinitas:\[ f'(x) = \left(\sum_{n=0}^\infty B_n\cdot {x^n\over n!}\right) \left(\sum_{n=0}^\infty a_n x^n\right) = f(x)g(x). \nonumber\] Encontrar una expresión para\(a_n\) que haga esto cierto, que le dirá lo que\(g(x)\) es, luego resolver la ecuación diferencial para\(f(x)\), la función generadora exponencial para los números de Bell. De la Sección 1.5, los primeros números de Campana son 1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, 678570, 4213597, 27644437. Puedes consultar tu respuesta en Sage.

# Enter your function here (e^x shown as an example):
f=exp(x)
# Now we compute the first few terms of the Taylor series, 
# extract the coefficients, and multiply by the factorial to
# get the part of the coefficients we want. 
g=f.taylor(x,0,13)
L=g.coefficients()
coeffs={c[1]:c[0]*factorial(c[1]) for c in L}
# coeffs is now a "dictionary" that holds pairs n:m, where
# n is the exponent and m is the coefficient. Note that
# coefficients with value zero are not included.
coeffs

3.4: Particiones de números enteros

Ejercicio\(\PageIndex{4.1}\)

Utilice funciones generadoras para encontrar\(p_{15}\).

Ejercicio\(\PageIndex{4.2}\)

Encuentra la función generadora para el número de particiones de un entero en distintas partes impares. Encuentra el número de tales particiones de 20.

Ejercicio\(\PageIndex{4.3}\)

Encuentra la función generadora para el número de particiones de un entero en partes pares distintas. Encuentra el número de tales particiones de 30.

Ejercicio\(\PageIndex{4.4}\)

Encuentra el número de particiones de 25 en partes impares.

Ejercicio\(\PageIndex{4.5}\)

Encuentra la función generadora para el número de particiones de un entero en\(k\) partes; es decir, el coeficiente de\(x^n\) es el número de particiones de\(n\) en\(k\) partes.

Ejercicio\(\PageIndex{4.6}\)

Completa la fila 8 de la tabla para el\(p_k(n)\), y verificar que la suma de filas es 22, como vimos en el Ejemplo 3.4.2.

Ejercicio\(\PageIndex{4.7}\)

Una partición de\(n\) es autoconjugada si su diagrama de Ferrers es simétrico alrededor de la diagonal principal, de manera que su conjugado es en sí mismo. Mostrar que el número de particiones autoconjugadas de\(n\) es igual al número de particiones de\(n\) en distintas partes impares.

3.5: Relaciones de recurrencia

Ejercicio\(\PageIndex{5.1}\)

Encuentre la función generadora de las soluciones a\(h_n=4h_{n-1}-3h_{n-2}\)\(h_0=2\),,\(h_1=5\), y úsela para encontrar una fórmula para\(h_n\).

Ejercicio\(\PageIndex{5.2}\)

Encuentre la función generadora para las soluciones a\(h_n=3h_{n-1}+4h_{n-2}\)\(h_0=h_1=1\), y úsela para encontrar una fórmula para\(h_n\).

Ejercicio\(\PageIndex{5.3}\)

Encuentre la función generadora para las soluciones a\(h_n=2h_{n-1}+3^n\)\(h_0=0\), y úsela para encontrar una fórmula para\(h_n\).

Ejercicio\(\PageIndex{5.4}\)

Encuentre la función generadora de las soluciones a\(h_n=4h_{n-2}\)\(h_0=0\),,\(h_1=1\), y úsela para encontrar una fórmula para\(h_n\). (Es fácil descubrir esta fórmula directamente; el punto aquí es ver que el enfoque de función generadora da la respuesta correcta).

Ejercicio\(\PageIndex{5.5}\)

Encuentre la función generadora de las soluciones a\(h_n=h_{n-1}+h_{n-2}\)\(h_0=1\),,\(h_1=3\), y úsela para encontrar una fórmula para\(h_n\).

Ejercicio\(\PageIndex{5.6}\)

Encuentre la función generadora de las soluciones a\(h_n=9h_{n-1}-26h_{n-2}+24h_{n-3}\)\(h_0=0\),\(h_1=1\),\(h_2=-1\), y úsela para encontrar una fórmula para\(h_n\).

Ejercicio\(\PageIndex{5.7}\)

Encuentre la función generadora de las soluciones a\(h_n=3h_{n-1}+4h_{n-2}\)\(h_0=0\),,\(h_1=1\), y úsela para encontrar una fórmula para\(h_n\).

Ejercicio\(\PageIndex{5.8}\)

Encuentra una recursión para la cantidad de formas de colocar banderas en un poste de\(n\) pie, donde tenemos banderas rojas que tienen 2 pies de alto, banderas azules que tienen 1 pie de alto y banderas amarillas que tienen 1 pie de alto; las alturas de las banderas deben sumar\(n\). Resolver la recursión.

Ejercicio\(\PageIndex{5.9}\)

En el problema original de Fibonacci, un agricultor comenzó con un par de conejos (recién nacidos) al mes 0. Después de que cada par de conejos tenía un mes de edad, producían otro par cada mes a perpetuidad. Así, después de 1 mes, tuvo el par original, después de dos meses 2 pares, tres meses, 3 pares, cuatro meses, 5 pares, etc. El número de parejas de conejos satisface\(h_n=h_{n-1}+h_{n-2}\),\(h_0=h_1=1\). (Tenga en cuenta que esto es ligeramente diferente a nuestra definición, en la que\(h_0=0\).)

Supongamos en cambio que cada pareja madura da a luz a dos parejas de conejos. La secuencia para el número de parejas de conejos comienza ahora\(h_0=1\),\(h_1=1\),\(h_2=3\),\(h_3=5\),\(h_4=11\). Establecer y resolver una relación de recurrencia para el número de parejas de conejos. Mostrar también que la secuencia satisface\(h_n=2h_{n-1}+(-1)^n\).

3.6: Números catalanes

Ejercicio\(\PageIndex{6.1}\)

Demostrar que\[ {2n\choose n}-{2n\choose n+1}={1\over n+1}{2n\choose n}. \nonumber\]

Ejercicio\(\PageIndex{6.2}\)

Encuentra una expresión simple\(f(n)\) para que\(C_{n+1}=f(n)C_n\). Utilice esto para calcular a\(C_1,\ldots,C_6\) partir de\(C_0\).

Ejercicio\(\PageIndex{6.3}\)

Mostrar que si\(A_n\) es el número de secuencias correctamente emparejadas de paréntesis de longitud\(2n\), entonces\[ A_n=\sum_{i=0}^{n-1} A_iA_{n-i-1}. \nonumber\] Haz esto en el mismo estilo que usamos para el número de árboles binarios enraizados: Dadas todas las secuencias de menor longitud, explica cómo combinarlas para producir las secuencias de longitud \(2n\), de tal manera que la suma cuenta claramente el número de secuencias. Pista: Demostrar el siguiente lema: Si\(s\) es una secuencia correctamente coincidente de paréntesis de longitud\(2n\), se\(s\) puede escribir de forma única en la forma\((s_1)s_2\), donde\(s_1\) y\(s_2\) son secuencias de paréntesis correctamente coincidentes cuyas longitudes se suman a\(2n-2\). Por ejemplo,\((())()= ([()])[()]\) y\(()(())=([\,])[(())]\), con las secuencias\(s_1\) e\(s_2\) indicadas por\([\,]\). Tenga en cuenta que\(s_1\) y\(s_2\) se les permite ser secuencias vacías, con longitud 0.

Ejercicio\(\PageIndex{6.4}\)

Considera una “escalera” como se muestra a continuación. Una ruta de\(A\) a\(B\) consiste en una secuencia de aristas que comienzan en\(A\), terminan en\(B\), y que continúan solo hacia arriba o hacia la derecha; todos los caminos son de longitud 6. Uno de esos caminos está indicado por flechas. La escalera que se muestra es una escalera\(3 \times 3\) "”. ¿Cuántos caminos hay en una\(n\times n\) escalera?

Figura\(\PageIndex{1}\)

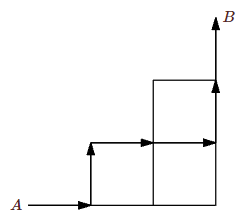
Ejercicio\(\PageIndex{6.5}\)

Un polígono convexo con\(n\ge3\) lados se puede dividir en triángulos insertando diagonales\(n-3\) que no se cruzan. ¿De cuántas maneras diferentes se puede hacer esto? Se\(n=5\) muestran las posibilidades para.

Figura\(\PageIndex{2}\)

Ejercicio\(\PageIndex{6.6}\)

Una partición de un conjunto\(S\) es una colección de subconjuntos no vacíos\(A_i\subseteq S\),\(1\le i\le k\) (las partes de la partición), tal que\(\bigcup_{i=1}^k A_i=S\) y para cada\(i\not=j\),\(A_i\cap A_j=\emptyset\). Por ejemplo, una partición de\(\{1,2,3,4,5\}\) es\(\{\{1,3\}\),\(\{4\}\),\(\{2,5\}\}\).

Supongamos que los enteros\(1,2,\ldots,n\) están dispuestos en un círculo, en orden alrededor del círculo. Una partición de\(\{1,2,\ldots,n\}\) es una partición no cruzada si satisface esta propiedad adicional: Si\(w\) y\(x\) están en alguna parte\(A_i\),\(y\) y\(z\) están en una parte diferente\(A_j\), entonces la línea que se une\(w\) a\(x\) no cruza el línea que se une\(y\) a\(z\). La partición anterior,\(\{1,3\}\),\(\{4\}\),\(\{2,5\}\), no es una partición no cruzada, ya que la línea 1—3 cruza la línea 2—5.

Encuentre el número de particiones no cruzadas de\(\{1,2,\ldots,n\}\).

Recordemos de la Sección 1.5 que los números de Campana cuentan todas las particiones de\(\{1,2,\ldots,n\}\). De ahí que este ejercicio nos dé un límite inferior sobre el número total de particiones.

Ejercicio\(\PageIndex{6.7}\)

Considera un conjunto de\(2n\) personas sentadas alrededor de una mesa. ¿De cuántas maneras podemos hacer arreglos para que cada persona estreche la mano de otra persona en la mesa de tal manera que no se crucen dos apretones de manos?