1.2: Operaciones de conjuntos básicos

Definiciones

Definición \(\PageIndex{1}\): Intersection

Dejar\(A\) y\(B\) ser conjuntos. La intersección de\(A\) y\(B\) (denotado por\(A \cap B\)) es el conjunto de todos los elementos que se encuentran en ambos\(A\) y es\(B\text{.}\) decir,\(A \cap B = \{x:x \in A \textrm{ and } x \in B\}\text{.}\)

Ejemplo\(\PageIndex{1}\): Some Intersections

• Let\(A = \{1, 3, 8\}\) y\(B = \{-9, 22, 3\}\text{.}\) Entonces\(A \cap B = \{3\}\text{.}\)
• Resolver un sistema de ecuaciones simultáneas como\(x + y = 7\) y\(x - y = 3\) puede ser visto como una intersección. Let\(A = \{(x,y): x + y = 7, x,y \in \mathbb{R}\}\) y\(B = \{(x,y): x - y = 3, x,y\in \mathbb{R}\}\text{.}\) Estos dos conjuntos son líneas en el plano y su intersección,\(A \cap B = \{(5, 2)\}\text{,}\) es la solución al sistema.
• \(\mathbb{Z}\cap \mathbb{Q}=\mathbb{Z}\text{.}\)
• Si\(A = \{3, 5, 9\}\) y\(B = \{-5, 8\}\text{,}\) entonces\(A\cap B =\emptyset\text{.}\)

Definición\(\PageIndex{2}\): Disjoint Sets

Dos conjuntos son disjuntos si no tienen elementos en común. Es decir,\(A\) y\(B\) son disjuntas si\(A \cap B = \emptyset\text{.}\)

Definición \(\PageIndex{3}\): Union

Dejar\(A\) y\(B\) ser conjuntos. La unión de\(A\) y\(B\) (denotada por\(A \cup B\)) es el conjunto de todos los elementos que están en\(A\) o en\(B\) o en ambos A y B. Es decir,\(A\cup B= \{x:x \in A\textrm{ or } x\in B\}\text{.}\)

Es importante señalar en la notación set-builder que\(A\cup B\text{,}\) la palabra “o” se usa en el sentido inclusivo; incluye el caso donde\(x\) está en ambos\(A\) y\(B\text{.}\)

Ejemplo\(\PageIndex{2}\): Some Unions

• Si\(A = \{2, 5, 8\}\) y\(B = \{7, 5, 22\}\text{,}\) entonces\(A \cup B = \{2, 5, 8, 7, 22\}\text{.}\)
• \(\displaystyle \mathbb{Z}\cup \mathbb{Q}=\mathbb{Q}.\)
• \(A \cup \emptyset = A\)para cualquier conjunto\(A\text{.}\)

Frecuentemente, al hacer matemáticas, necesitamos establecer un universo o conjunto de elementos en discusión. Por ejemplo, el conjunto\(A = \{x : 81x^4 -16 = 0 \}\) contiene diferentes elementos dependiendo de qué tipo de números nos permitimos utilizar para resolver la ecuación\(81 x^4 -16 = 0\text{.}\) Este conjunto de números sería nuestro universo. Por ejemplo, si el universo son los enteros, entonces\(A\) está vacío. Si nuestro universo son los números racionales, entonces\(A\) es\(\{2/3, -2/3\}\) y si el universo son los números complejos, entonces\(A\) es\(\{2/3, -2/3, 2i/3, - 2i/3\}\text{.}\)

Definición\(\PageIndex{4}\): Universe

El universo, o conjunto universal, es el conjunto de todos los elementos en discusión para una posible pertenencia a un conjunto. Normalmente reservamos la carta\(U\) para un universo en las discusiones generales.

Operaciones y sus Diagramas Venn

Cuando se trabaja con conjuntos, como en otras ramas de las matemáticas, suele ser bastante útil poder dibujar un cuadro o diagrama de la situación en consideración. Un diagrama de un conjunto se llama diagrama de Venn. El conjunto universal\(U\) está representado por el interior de un rectángulo y los conjuntos por discos dentro del rectángulo.

Ejemplo\(\PageIndex{3}\): Venn Diagram Examples

\(A \cap B\)se ilustra en la Figura\(\PageIndex{1}\) sombreando la región apropiada.

Figura Diagrama de\(\PageIndex{1}\): Venn para la Intersección de Dos Conjuntos

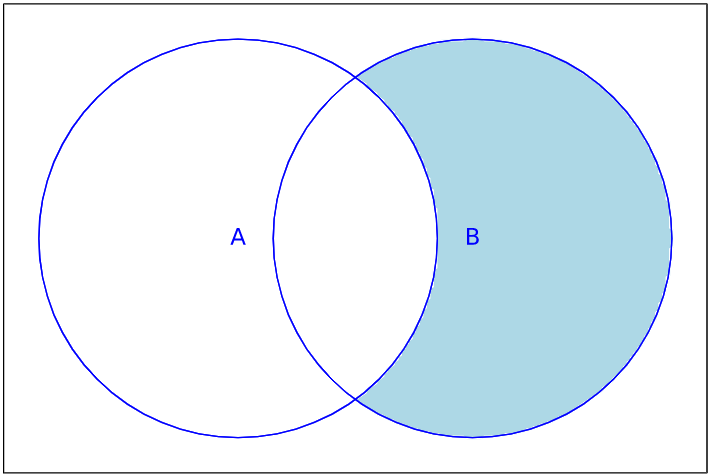
La unión\(A \cup B\) se ilustra en la Figura\(\PageIndex{2}\).

Figura Diagrama de\(\PageIndex{2}\): Venn para la Unión\(A \cup B\)

En un diagrama de Venn, la región que representa\(A \cap B\) no aparece vacía; sin embargo, en algunos casos representará el conjunto vacío. Lo mismo es cierto para cualquier otra región en un diagrama de Venn.

Definición \(\PageIndex{5}\): Complement of a Set

Dejar\(A\) y\(B\) ser conjuntos. El complemento de\(A\) relativo a\(B\) (notación\(B - A\)) es el conjunto de elementos que están en\(B\) y no en Es\(A\text{.}\) decir,\(B-A=\{x: x\in B \textrm{ and } x\notin A\}\text{.}\) si\(U\) es el conjunto universal, entonces\(U-A\) se denota por\(A^c\) y se llama simplemente el complemento de\(A\text{.}\)\(A^c=\{x\in U : x\notin A\}\text{.}\)

Figura Diagrama de\(\PageIndex{3}\): Venn para\(B - A\)

Ejemplo\(\PageIndex{4}\): Some Complements

1. Dejar\(U = \{1,2, 3, \text{...} , 10\}\) y\(A = \{2,4,6,8, 10\}\text{.}\) Entonces\(U-A = \{1, 3, 5, 7, 9\}\) y\(A - U= \emptyset\text{.}\)
2. Si\(U = \mathbb{R}\text{,}\) entonces el complemento del conjunto de números racionales es el conjunto de números irracionales.
3. \(U^c= \emptyset\)y\(\emptyset ^c= U\text{.}\)
4. El diagrama de Venn\(B - A\) se representa en la Figura\(\PageIndex{3}\).
5. El diagrama de Venn\(A^c\) se representa en la Figura\(\PageIndex{4}\).
6. Si\(B\subseteq A\text{,}\) entonces el diagrama de Venn de\(A- B\) es como se muestra en la Figura\(\PageIndex{5}\).
7. En el universo de enteros, el conjunto de enteros pares,\(\{\ldots , - 4,-2, 0, 2, 4,\ldots \}\text{,}\) tiene como complemento el conjunto de enteros impares.

Figura Diagrama de\(\PageIndex{4}\): Venn para\(A^{c}\)

Figura Diagrama de\(\PageIndex{5}\): Venn para\(A-B\) when \(B\) is a subset of \(A\)

Definición \(\PageIndex{6}\): Symmetric Difference

Dejar\(A\) y\(B\) ser conjuntos. La diferencia simétrica de\(A\) y\(B\) (denotada por\(A\oplus B\)) es el conjunto de todos los elementos que están en\(A\) y\(B\) pero no en ambos. Es decir,\(A \oplus B = (A \cup B) - (A \cap B)\text{.}\)

Ejemplo\(\PageIndex{5}\): Some Symmetric Differences

1. Let\(A = \{1, 3, 8\}\) y\(B = \{2, 4, 8\}\text{.}\) Entonces\(A \oplus B = \{1, 2, 3, 4\}\text{.}\)
2. \(A \oplus \emptyset = A\)y\(A \oplus A = \emptyset\) para cualquier conjunto\(A\text{.}\)
3. \(\mathbb{R} \oplus \mathbb{Q}\)es el conjunto de números irracionales.
4. El diagrama de Venn\(A \oplus B\) se representa en la Figura\(\PageIndex{6}\).

Figura Diagrama de\(\PageIndex{6}\): Venn para la diferencia simétrica\(A \oplus B\)

Nota de SageMath: Sets

Para trabajar con conjuntos en Sage, un conjunto es una expresión del formulario Set (list). Al envolver una lista con Set (), se ignora el orden de los elementos que aparecen en la lista y su duplicación. Por ejemplo, L1 y L2 son dos listas diferentes, pero observe cómo como conjuntos se consideran iguales:

L1=[3,6,9,0,3]
L2=[9,6,3,0,9]
[L1==L2, Set(L1)==Set(L2) ]

Las operaciones de conjunto estándar son todos métodos y/o funciones que pueden actuar sobre conjuntos de Sage. Es necesario evaluar la siguiente celda para usar la celda posterior.

A=Set(srange(5,50,5))
B=Set(srange(6,50,6))
[A,B]

Podemos probar la membresía, preguntándonos si 10 está en cada uno de los conjuntos:

[10 in A, 10 in B]

El ampersand se utiliza para la intersección de conjuntos. Cámbielo a la barra vertical, |, para unión.

A & B

La diferencia simétrica y el complemento conjunto se definen como “métodos” en Sage. Aquí se explica cómo calcular la diferencia simétrica de\(A\) con\(B\text{,}\) seguida de sus diferencias.

[A.symmetric_difference(B),A.difference(B),B.difference(A)]

Ejercicios

Ejercicio\(\PageIndex{1}\)

Deje\(A = \{0, 2, 3\}\text{,}\)\(B = \{2, 3\}\text{,}\)\(C = \{1, 5, 9\}\text{,}\) y deje que el conjunto universal sea\(U = \{0, 1, 2, . . . , 9\}\text{.}\) Determine:

1. \(\displaystyle A \cap B\)
2. \(\displaystyle A \cup B\)
3. \(\displaystyle B \cup A\)
4. \(\displaystyle A \cup C\)
5. \(\displaystyle A - B\)
6. \(\displaystyle B - A\)
7. \(\displaystyle A^c\)
8. \(\displaystyle C^c\)
9. \(\displaystyle A\cap C\)
10. \(\displaystyle A\oplus B\)

Contestar

1. \(\displaystyle \{2,3\}\)
2. \(\displaystyle \{0,2,3\}\)
3. \(\displaystyle \{0,2,3\}\)
4. \(\displaystyle \{0,1,2,3,5,9\}\)
5. \(\displaystyle \{0\}\)
6. \(\displaystyle \emptyset\)
7. \(\displaystyle \{ 1,4,5,6,7,8,9\}\)
8. \(\displaystyle \{0,2,3,4,6,7,8\}\)
9. \(\displaystyle \emptyset\)
10. \(\displaystyle \{0\}\)

Ejercicio\(\PageIndex{2}\)

Dejar\(A\text{,}\)\(B\text{,}\) y\(C\) ser como en el Ejercicio 1, dejar\(D = \{3, 2\}\text{,}\) y dejar\(E = \{2, 3, 2\}\text{.}\) Determinar cuáles de los siguientes son ciertos. Dé razones de sus decisiones.

1. \(\displaystyle A = B\)
2. \(\displaystyle B = C\)
3. \(\displaystyle B = D\)
4. \(\displaystyle E=D\)
5. \(\displaystyle A\cap B = B\cap A\)
6. \(\displaystyle A \cup B = B \cup A\)
7. \(\displaystyle A-B = B-A\)
8. \(\displaystyle A \oplus B = B \oplus A\)

Ejercicio\(\PageIndex{3}\)

Vamos\(U= \{1, 2, 3, . . . , 9\}\text{.}\) Dar ejemplos de conjuntos\(A\text{,}\)\(B\text{,}\) y\(C\) para los cuales:

1. \(\displaystyle A\cap (B\cap C)=(A\cap B)\cap C\)
2. \(\displaystyle A\cap (B\cup C)=(A\cap B)\cup (A\cap C)\)
3. \(\displaystyle (A \cup B)^c= A^c\cap B^c\)
4. \(\displaystyle A \cup A^c = U\)
5. \(\displaystyle A \subseteq A\cup B\)
6. \(\displaystyle A\cap B \subseteq A\)

Contestar

Todos estos son ciertos para cualquier conjunto\(A\text{,}\)\(B\text{,}\) y\(C\text{.}\)

Ejercicio\(\PageIndex{4}\)

Vamos\(U= \{1, 2, 3, . . . , 9\}\text{.}\) Dar ejemplos para ilustrar los siguientes hechos:

1. Si\(A \subseteq B\) y\(B \subseteq C\text{,}\) entonces\(A\subseteq C\text{.}\)
2. Hay conjuntos\(A\) y\(B\) tal que\(A - B \neq B - A\)
3. Si\(U = A\cup B\) y siempre\(A \cap B = \emptyset\text{,}\) se deduce que\(A = U - B\text{.}\)

Ejercicio\(\PageIndex{5}\)

¿Qué puedes decir sobre\(A\) si\(U = \{1, 2, 3, 4, 5\}\text{,}\)\(B = \{2, 3\}\text{,}\) y (por separado)

1. \(\displaystyle A \cup B = \{1, 2, 3,4\}\)
2. \(\displaystyle A \cap B = \{2\}\)
3. \(\displaystyle A \oplus B = \{3, 4, 5\}\)

Contestar

1. \(\displaystyle \{1, 4\} \subseteq A \subseteq \{1, 2, 3, 4\}\)
2. \(\displaystyle \{2\} \subseteq A \subseteq \{1, 2, 4, 5\}\)
3. \(\displaystyle A = \{2, 4, 5\}\)

Ejercicio\(\PageIndex{6}\)

Supongamos que\(U\) es un conjunto universal infinito,\(A\) y\(B\) son infinitos subconjuntos de\(U\text{.}\) Responde las siguientes preguntas con una breve explicación.

1. ¿Debe\(A^c\) ser finito?
2. ¿Debe\(A\cup B\) ser infinito?
3. ¿Debe\(A\cap B\) ser infinito?

Ejercicio\(\PageIndex{7}\)

Dado que\(U\) = todos los estudiantes de una universidad,\(D\) = estudiantes de día,\(M\) = carreras de matemáticas, y\(G\) = estudiantes de posgrado. Dibuja diagramas de Venn que ilustren esta situación y sombree en los siguientes conjuntos:

1. estudiantes vespertinos
2. carreras de matemáticas de pregrado
3. estudiantes de posgrado no matemáticos
4. estudiantes de pregrado no matemáticos

Contestar

Figura\(\PageIndex{7}\): Solución al ejercicio\(\PageIndex{7}\) de la Sección 1.2.

Ejercicio\(\PageIndex{8}\)

Deja los sets\(D\text{,}\)\(M\text{,}\)\(G\text{,}\) y\(U\) sé como en el ejercicio 7. Vamos\(\lvert U \rvert = 16,000\text{,}\)\(\lvert D \rvert = 9,000\text{,}\)\(|M|= 300\text{,}\) y Supongamos\(\lvert G \rvert = 1,000\text{.}\) también que el número de estudiantes de día que son carreras de matemáticas es de 250, 50 de los cuales son estudiantes de posgrado, que hay 95 carreras de posgrado en matemáticas, y que el número total de estudiantes de posgrado diurno es de 700. Determinar el número de alumnos que son:

1. estudiantes vespertinos
2. carreras de no matemáticas
3. estudiantes universitarios (de día o de noche)
4. día de posgrado no matemáticas mayores
5. estudiantes de posgrado vespertino
6. egresado vespertino de matemáticas
7. licenciatura vespertina no matemáticas mayores