2.3: Particiones de Conjuntos y Ley de Adición

Última actualización
Guardar como PDF

Page ID: 117300

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Particiones

Una forma de contar el número de alumnos en tu clase sería contar el número en cada fila y sumar estos totales. Por supuesto que este problema es sencillo porque no hay duplicaciones, ninguna persona está sentada en dos filas distintas. La técnica básica de conteo que utilizaste implica un primer paso sumamente importante, a saber, el de particionar un conjunto. El concepto de partición debe entenderse claramente antes de continuar.

Definición$\PageIndex{1}$: Partition

Una partición de conjunto$A$ es un conjunto de uno o más subconjuntos no vacíos de$A\text{:}$$A_1, A_2, A_3, \cdots\text{,}$ tal manera que cada elemento de$A$ está exactamente en un conjunto. Simbólicamente,

$\displaystyle A_1 \cup A_2 \cup A_3 \cup \cdots = A$
Si$i \neq j$ entonces$A_i \cap A_j = \emptyset$

Los subconjuntos en una partición a menudo se denominan bloques. Observe cómo nuestra definición nos permite particionar conjuntos infinitos, y particionar un conjunto en un número infinito de subconjuntos. Por supuesto, si$A$ es finito el número de subconjuntos no puede ser mayor que$\lvert A \rvert \text{.}$

Ejemplo$\PageIndex{1}$: Some Partitions of a Four Element Set

Let$A = \{a, b, c, d\}\text{.}$ Ejemplos de particiones de$A$ son:

$\displaystyle \{\{a\}, \{b\}, \{c, d\}\}$
$\displaystyle \{\{a, b\}, \{c, d\}\}$
$\displaystyle \{\{a\}, \{b\}, \{c\}, \{d\}\}$

¿Cuántos otros hay, supongo?

Hay 15 particiones diferentes. La forma más eficiente de contarlos todos es clasificarlos por el tamaño de los bloques. Por ejemplo, la partición$\{\{a\}, \{b\}, \{c, d\}\}$ tiene tamaños de bloque 1, 1 y 2.

Ejemplo$\PageIndex{2}$: Some Integer Partitions

Dos ejemplos de particiones de conjunto de enteros$\mathbb{Z}$ son

$\{\{n\} \mid n \in \mathbb{Z}\}$y
$\{\{ n \in \mathbb{Z} \mid n < 0\}, \{0\},\{ n \in \mathbb{Z} \mid 0 < n \}\}\text{.}$

El conjunto de subconjuntos no$\{\{n \in \mathbb{Z} \mid n \geq 0\},\{n \in \mathbb{Z} \mid n \leq 0\}\}$ es una partición porque los dos subconjuntos tienen una intersección no vacía. Un segundo ejemplo de una no-partición es$\{\{n \in \mathbb{Z} \mid \lvert n \rvert = k\} \mid k = -1, 0, 1, 2, \cdots\}$ porque uno de los bloques, cuando$k=-1$ está vacío.

También se podría pensar en el concepto de particionar un conjunto como un “problema de empaque”. ¿Cómo se puede “empaquetar” una caja de, digamos, veinticuatro latas? Podríamos usar: cuatro paquetes de seis, tres paquetes de ocho, dos paquetes de doce, etc. En todos los casos: (a) la suma de todas las latas en todos los paquetes debe ser veinticuatro, y (b) una lata debe estar en uno y solo un paquete.

Leyes de Adición

Teorema$\PageIndex{1}$: The Basic Law of Addition

Si$A$ es un conjunto finito, y si$\{A_1,A_2,\ldots ,A_n\}$ es una partición de$A$, entonces

\[\lvert A \rvert = \lvert A_1 \rvert + \lvert A_2 \rvert + \cdots + \lvert A_n \rvert = \sum_{k=1}^n \lvert A_k \rvert \nonumber\]

La ley básica de adición puede reformularse de la siguiente manera: Si$A$ es un conjunto finito donde$A_1 \cup A_2 \cup \cdots \cup A_n = A$ y donde$A_i \cap A_j = \emptyset$ siempre que$i \neq j\text{,}$ entonces

\ begin {ecuación*}\ lvert A\ rvert =\ lvert A-1\ copa A_2\ copa\ cdots\ copa a_n\ rvert =\ lvert A-1\ rvert +\ lvert A_2\ rvert +\ cdots +\ lvert a_N\ rvert\ end {ecuación*}

Ejemplo$\PageIndex{3}$: Counting All Students

El número de alumnos en una clase podría determinarse sumando los números de estudiantes que son estudiantes de primer año, segundo año, juniors y seniors, y aquellos que pertenecen a ninguna de estas categorías. Sin embargo, probablemente no podrías sumar a los estudiantes por especialidad, ya que algunos estudiantes pueden tener dobles carreras.

Ejemplo$\PageIndex{4}$: Counting Students in Disjoint Classes

A los estudiantes de segundo año se les dijo que debían tomar uno y solo uno de los siguientes cursos que solo están abiertos a ellos: Criptografía, Estructuras de Datos o Javascript. Los números en cada curso, respectivamente, para las mayores CS de segundo año, fueron 75, 60, 55. ¿Cuántos mayores de segundo año de CS hay? Aquí se aplica la Ley de Adición. Hay exactamente mayores$75 + 60 + 55 = 190$ CS ya que las listas de los tres cursos enumerados anteriormente serían una partición de las mayores CS.

Ejemplo$\PageIndex{5}$: Counting Students in Non-Disjoint Classes

Se determinó que todas las carreras junior en ciencias de la computación toman al menos uno de los siguientes cursos: Algoritmos, Diseño Lógico y Construcción de Compiladores. Supongamos que el número en cada curso fue de 75, 60 y 55, respectivamente para los tres cursos enumerados. Investigaciones adicionales indicaron que diez jóvenes tomaron los tres cursos, veinticinco tomaron Algoritmos y Diseño Lógico, doce tomaron Algoritmos y Construcción de Compiladores, y quince tomaron Diseño Lógico y Construcción de Compiladores. ¿Cuántas carreras junior de C.S. hay?

Ejemplo$\PageIndex{4}$ fue una simple aplicación de la ley de adición, sin embargo en este ejemplo algunos alumnos están tomando dos o más cursos, por lo que una simple aplicación de la ley de adición llevaría a contar doble o triple. Reformulamos la información en el lenguaje de los conjuntos para describir la situación de manera más explícita.

$A$= el conjunto de todas las carreras de ciencias de la computación junior

$A_1$= el conjunto de todas las carreras de informática junior que tomaron Algoritmos

$A_2$= el conjunto de todos los estudiantes menores de ciencias de la computación que tomaron Diseño Lógico

$A_3$= el conjunto de todas las carreras de informática junior que tomaron Compiler Construction

Dado que todas las carreras junior CS deben tomar al menos uno de los cursos, el número que queremos es:

\ begin {ecuación*}\ lvert A\ rvert =\ lvert A-1\ copa A_2\ copa A_3\ rvert =\ lvert A-1\ rvert +\ lvert A_2\ rvert +\ lvert A_3\ rvert -\ textrm {repite}. \ end {ecuación*}

Un diagrama de Venn es útil para visualizar el problema. En este caso el conjunto universal$U$ puede representar a todos los estudiantes de la universidad.

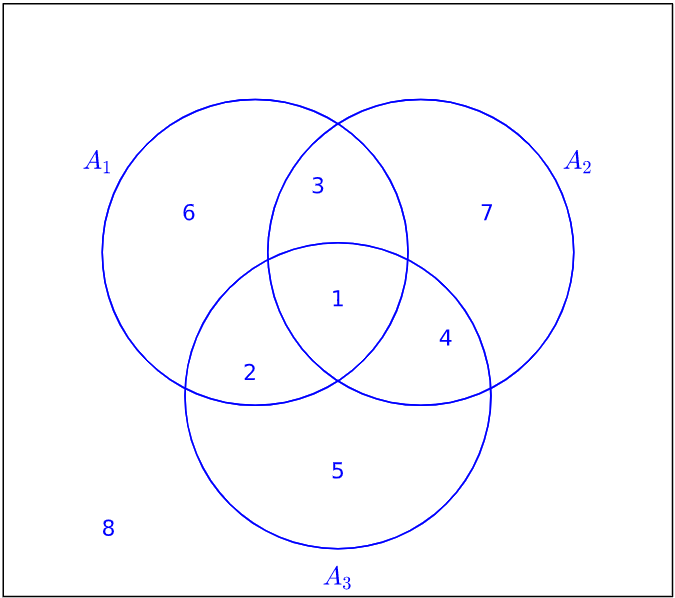
$clipboard_ed267365ef05c6471fcaef3cc88db44e0.png$

Figura$\PageIndex{1}$: Diagrama de Venn

Vemos que todo el conjunto universal se divide naturalmente en subconjuntos que están etiquetados por los números del 1 al 8, y el conjunto$A$ se divide en subconjuntos etiquetados del 1 al 7. La región etiquetada con 8 representa a todos los estudiantes que no son mayores de CS junior. Tenga en cuenta también que los estudiantes en los subconjuntos etiquetados 2, 3 y 4 son contados dobles, y los del subconjunto etiquetado 1 son contados triples. Para ajustar, debemos restar los números en las regiones 2, 3 y 4. Esto se puede hacer restando los números en las intersecciones de cada par de conjuntos. No obstante, los individuos de la región 1 habrán sido removidos tres veces, tal como se habían agregado originalmente tres veces. Por lo tanto, por fin debemos volver a sumar su número.

\ begin {ecuation*}\ begin {split}\ lvert A\ rvert & =\ lvert A-1\ copa A_2\ copa A_3\ rvert\\ & =\ lvert A-1\ rvert +\ lvert A_2\ rvert +\ lvert A_3\ rvert -\ textrm {repite}\\ & =\ lvert A-1\ rvert +\ lvert A_2\ rvert +\ lvert A_3\ rvert -\ textrm {duplicados} +\ textrm {triplicados}\\ & =\ lvert A_ 1\ rvert +\ lvert A_2\ rvert +\ lvert A_3\ rvert -\ izquierda (\ lvert A-1\ cap A_2\ rvert +\ lvert A-1\ cap A_3\ rvert+\ lvert A_2\ cap A_3\ rvert\ rvert\ derecha) +\ lvert A-1\ cap A_2\ cap A_3\ rvert\ & = 75 + 60 + 55 - 25 - 12 - 15 + 10 = 148\ end {split}\ end {ecuación*}

Las ideas utilizadas en este último ejemplo dan lugar a una técnica básica de conteo:

Teorema$\PageIndex{2}$: Laws of Inclusion-Exclusion

Dados conjuntos finitos$A_1, A_2, A_3\text{,}$ entonces

La Ley de Inclusión-Exclusión de Dos Conjuntos:
\ begin {ecuation*}\ lvert A-1\ cup A_2\ rvert =\ lvert A-1\ rvert +\ lvert A_2\ rvert -\ lvert A_1\ cap A_2\ rvert\ end {ecuación*}
La Ley de Inclusión-Exclusión de Tres Conjuntos:
\ begin {equation*}\ begin {split}\ lvert A-1\ cup A_2\ cup A_3\ rvert & =\ lvert A-1\ rvert +\ lvert A_2\ rvert +\ lvert A_3\ rvert\ rvert\\ &\ quad - (\ lvert A_1\ cap A_2\ rvert +\ lvert A-1\ cap A_3\ rvert+\ lvert A_2\ cap A_3\ rvert)\\ &\ quad +\ lvert A_1\ cap A_2\ cap A_3\ rvert\ end {split}\ end {ecuación*}

Las leyes de inclusión-exclusión se extienden a más de tres conjuntos, como se explorará en los ejercicios.

En esta sección vimos que poder dividir un conjunto en subconjuntos disjuntos da lugar a una práctica técnica de conteo. Dado un conjunto, hay muchas formas de particionar dependiendo de lo que uno quisiera lograr. Una partición natural de conjuntos es evidente cuando se dibuja un diagrama de Venn. Esta partición particular de un conjunto se discutirá más a fondo en los Capítulos 4 y 13.

Ejercicios

Ejercicio$\PageIndex{1}$

Listar todas las particiones del conjunto$A =\{a, b, c\}\text{.}$

Responder: $\{\{a\}, \{b\}, \{c\}\}, \{\{a, b\}, \{c\}\}, \{\{a, c\}, \{b\}\}, \{\{a\}, \{b, c\}\}, \{\{a, b, c\}\}$

Ejercicio$\PageIndex{2}$

¿Cuáles de las siguientes colecciones de subconjuntos del plano,$\mathbb{R}^2\text{,}$ son particiones?

$\displaystyle \{ \{(x, y) \mid x + y = c \} \mid c \in \mathbb{R} \}$
El conjunto de todos los círculos en$\mathbb{R}^2 $
El conjunto de todos los círculos en$\mathbb{R}^2$ centrado en el origen junto con el conjunto$\{(0,0)\}$
$\displaystyle \{\{(x, y)\} \mid (x, y) \in \mathbb{R}^2 \} $

Ejercicio$\PageIndex{3}$

Un alumno, en un papel de examen, definió el término partición de la siguiente manera: “Let$A$ be a set. Una partición de$A$ es cualquier conjunto de subconjuntos no vacíos$A_1, A_2, A_3, \dots$ de$A$ tal manera que cada elemento de$A$ está en uno de los subconjuntos”. ¿Es correcta esta definición? ¿Por qué?

Responder: No. Por esta definición es posible que un elemento de$A$ pudiera pertenecer a dos de los subconjuntos.

Ejercicio$\PageIndex{4}$

Dejar$A_1$ y$A_2$ ser subconjuntos de un conjunto$U\text{.}$ Dibuja un diagrama de Venn de esta situación y sombra en los subconjuntos$A_1 \cap A_2\text{,}$$A_1^c \cap A_2\text{,}$$A_1 \cap A_2^c\text{,}$ y$A_1^c \cap A_2^c$. Usa el diagrama resultante y la definición de partición para convencerte de que el subconjunto de estos cuatro subconjuntos que no están vacíos forman una partición de$U\text{.}$

Ejercicio$\PageIndex{5}$

Mostrar que$\{\{2 n \mid n \in \mathbb{Z}\}, \{2 n + 1 \mid n \in \mathbb{Z}\}\}$ es una partición de$\mathbb{Z}\text{.}$ Describe esta partición usando solo palabras.

Responder: El primer subconjunto es todos los enteros pares y el segundo son todos los enteros impares. Estos dos conjuntos no se cruzan y cubren completamente los enteros.

Ejercicio$\PageIndex{6}$

Se encuestó a un grupo de 30 estudiantes y se encontró que 18 de ellos tomaron Cálculo y 12 tomaron Física. Si todos los estudiantes tomaron al menos un curso, ¿cuántos tomaron tanto Cálculo como Física? Ilustrar usando un diagrama de Venn.
¿Cuál es la respuesta a la pregunta de la parte (a) si cinco alumnos no tomaron ninguno de los dos cursos? Ilustrar usando un diagrama de Venn.

Ejercicio$\PageIndex{7}$

Una encuesta a 90 personas, 47 de ellas jugaron tenis y 42 de ellas nadaron. Si 17 de ellos participaron en ambas actividades, ¿cuántos de ellos participaron en ninguna?

Responder: Ya que 17 participaron en ambas actividades, 30 de los tenistas solo jugaron tenis y 25 de los nadadores solo nadaron. Por lo tanto,$17+30+25=72$ de los encuestados participaron en una actividad y por lo tanto 18 no lo hicieron.

Ejercicio$\PageIndex{8}$

Una encuesta a 300 personas encontró que 60 eran dueños de un iPhone, 75 tenían un Blackberry y 30 tenían un teléfono Android. Además, 40 poseían tanto un iPhone como un Blackberry, 12 poseían tanto un iPhone como un teléfono Android, y 8 poseían un Blackberry y un teléfono Android. Por último, 3 poseían los tres teléfonos.

¿Cuántas personas encuestadas no poseían ninguno de los tres teléfonos?
¿Cuántas personas poseían un Blackberry pero no un iPhone?
¿Cuántos poseían un Blackberry pero no un Android?

Ejercicio$\PageIndex{9}$

En cuanto al teorema$\PageIndex{2}$,

Utilice las dos leyes de inclusión-exclusión establecidas para derivar la ley de inclusión-exclusión de tres conjuntos. Nota: Para este ejercicio se necesita un conocimiento de las leyes básicas establecidas.
Estado y derivar la ley de inclusión-exclusión para cuatro conjuntos.

Responder

Suponemos que$\lvert A_1 \cup A_2 \rvert = \lvert A_1 \rvert +\lvert A_2\rvert -\lvert A_1\cap A_2\rvert \text{.}$

\ begin {equation*}\ begin {split}\ lvert A_1\ copa A_2\ copa A_3\ rvert & =\ lvert (A_1\ copa A_2)\ copa A_3\ rvert\ quad ¿Por qué? \\ & =\ lvert A-1\ copa A_2\ rvert +\ lvert A_3\ rvert -\ lvert (A-1\ copa A_2)\ cap A_3\ rvert\ quad ¿Por qué? \\ & =\ lvert (A-1\ copa A_2\ rvert +\ lvert A_3\ rvert -\ lvert (A-1\ cap A_3)\ copa (A_2\ cap A_3)\ rvert\ quad ¿Por qué? \\ & =\ lvert A-1\ rvert +\ lvert A_2\ rvert -\ lvert A-1\ cap A_2\ rvert +\ lvert A_3\ rvert\\ rvert\\ &\ quad - (\ lvert A-1\ cap A_3\ rvert +\ lvert A_2\ cap A_3\ rvert -\ lvert (A_1\ cap A_3)\ cap (A_2 cap\ A_3)\ rvert\ quad ¿Por qué? \\ & =\ lvert A-1\ rvert +\ lvert A-2\ rvert +\ lvert A_3\ rvert -\ lvert A-1\ cap A_2\ rvert -\ lvert A-1\ cap A_3\ rvert\\ &\ quad -\ lvert A_2\ cap A_3\ rvert +\ lvert A-1\ cap quad A_2\ cap A_3\ rvert\ Por qué? \ end {split}\ end {ecuación*}

La ley para cuatro conjuntos es

\ begin {ecuation*}\ begin {split}\ lvert A-1\ copa A_2\ copa A_3\ copa A_4\ rvert & =\ lvert A-1\ rvert +\ lvert A_2\ rvert +\ lvert A_3\ rvert +\ lvert A_4\ rvert\ &\ quad -\ lvert A_1\ cap A_2\ rvert -\ lvert A_1\ cap A_3\ rvert -\ lvert A-1\ cap A_4\ rvert\\ &\ quad\ quad -\ lvert A_2\ cap A_3\ rvert -\ lvert A_2\ cap A_4\ rvert -\ lvert A_3\ cap A_4\ rvert\\ &\ quad +\ lvert A-1\ cap A_2\ cap A_3\ rvert +\ lvert A-1\ cap A_2\ cap A_4\ rvert\\ rvert\\ &\ quad +\ lvert A-1\ cap A_3\ cap A_3\ cap A_3\ cap A_4\ rvert +\ rvert +\ lvert A_2\ cap A_3\ cap A_4\ rvert vert\\ &\ quad -\ lvert A-1\ cap A_2\ cap A_3\ cap A_4\ rvert\ end {split}\ end {equation*}

Derivación:

\ begin {ecuation*}\ begin {split}\ lvert A_1\ copa A_2\ copa A_3\ copa A_4\ rvert & =\ lvert (A_1\ copa A_2\ copa A_3)\ copa A_4\ rvert\\ rvert\\ & =\ lvert (A_1\ copa A_3\ rvert +\ lvert A_4\ rvert -\ lvert (A_1\ copa A_3\ rvert +\ lvert A_4\ rvert -\ copa A_2\ copa A_3)\ tapa A_4\ rvert\\ & =\ lvert (A-1\ copa A_2\ copa A_3\ rvert +\ lvert A_4\ rvert\\ rvert\\ &\ quad -\ lvert (A-1\ cap A_4)\ copa (A_2\ cap A_4)\ copa (A_3\ cap A_4)\ rvert\\ & =\ lvert A-1\ rvert +\ lvert A_2\ rvert +\ lvert A_3\ rvert -\ lvert A-1\ cap A_2\ rvert -\ lvert A_1\ quad cap A_3\ rvert\\ &\ -\ lvert A_2\ cap A_3\ rvert +\ lvert A-1\ cap A_2\ cap A_3\ rvert +\ lvert A_4\ rvert -\ lvert A-1\ cap A_4\ rvert\\ &\ quad+\ lvert A_2\ cap A_4\ rvert +\ lvert A_3\ cap A_4\ rvert -\ lvert (A_1\ cap A_4)\ cap (A_2\ cap A_4)\ rvert\\ rvert (A_1\ cap A_4)\ cap (A_3\ cap A_4)\ rvert -\ lvert (A_2\ cap A_4) cap\ (A_3\ cap A_4)\ rvert\\ &\ quad +\ lvert (A-1\ cap A_4)\ cap (A_2\ cap A_4)\ cap (A_3\ cap A_4)\ rvert\\ & =\ lvert A-1\ rvert +\ lvert A_2\ rvert +\ lvert A_3\ rvert +\ lvert A_4\ rvert -\ lvert A-1\ cap A_2\ rvert -\ lvert A-1\ cap A_3\ rvert\\ rvert\ &\ quad -\ lvert A_2\ cap A_3\ rvert -\ lvert A_1\ cap A_4\ rvert -\ rvert A_2\ cap A_4\ vert\ quad -\ lvert A_3\ cap A_4\ rvert\\ &\ quad +\ lvert A-1\ cap A_2\ cap A_3\ rvert +\ lvert A-1\ cap A_2\ cap A_4\ rvert\\ rvert\\ &\ quad +\ lvert A-1\ cap A_3\ cap A_4\ rvert +\ lvert A_2\ cap A_3\ cap A_4\ rvert\\ &\ quad -\ lvert A-1\ cap A_2\ cap A_3\ cap A_4\ rvert\ end {split}\ end {ecuación*}

Ejercicio$\PageIndex{10}$

Para completar tu horario de primavera, debes agregar Cálculo y Física. A las 9:30, hay tres secciones de Cálculo y dos secciones de Física; mientras que a las 11:30, hay dos secciones de Cálculo y tres secciones de Física. ¿De cuántas maneras puedes completar tu horario si tus únicos periodos abiertos son las 9:30 y las 11:30?

Ejercicio$\PageIndex{11}$

La definición de$\mathbb{Q} = \{a/b \mid a, b \in \mathbb{Z}, b \neq 0\}$ dado en el Capítulo 1 es incómoda. Si usamos la definición para enumerar elementos en$\mathbb{Q}\text{,}$ tendremos duplicaciones como$\frac{1}{2}\text{,}$$\frac{-2}{-4}$ e$\frac{300}{600}$ intentar escribir una definición más precisa de los números racionales para que no haya duplicación de elementos.

Responder: Dividir el conjunto de fracciones en bloques, donde cada bloque contiene fracciones que son numéricamente equivalentes. Describe cómo determinarías si dos fracciones pertenecen al mismo bloque. Redefinir los números racionales para que sean esta partición. Cada número racional es un conjunto de fracciones.