2.4: Las combinaciones y el teorema del binomio

Combinaciones

En la Sección 2.1 investigamos el concepto más básico en combinatoria, es decir, la regla de los productos. Es de suma importancia tener presente esta regla fundamental. En la Sección 2.2 vimos una subclase de problemas de reglas de productos, permutaciones, y derivamos una fórmula como ayuda computacional para asistirnos. En esta sección investigaremos otra fórmula de conteo, una que se utiliza para contar combinaciones, que son subconjuntos de cierto tamaño.

En muchas aplicaciones de reglas de productos el pedido es importante, como el orden de bateo de un equipo de béisbol. En otros casos no es importante, como en colocar monedas en una máquina expendedora o en el listado de los elementos de un conjunto. El orden es importante en las permutaciones. El orden no es importante en las combinaciones.

Ejemplo$\PageIndex{1}$: Counting Permutations

Cuantas formas diferentes hay de permutar tres letras del conjunto$A = \{a, b, c, d\}\text{?}$ De la Fórmula de Conteo de Permutaciones, Teorema 2.2.1, hay$P(4,3)=\frac{4!}{(4-3)!} = 24$ diferentes ordenamientos de tres letras de$A$

Ejemplo$\PageIndex{2}$: Counting with No Order

De cuántas maneras podemos seleccionar un conjunto de tres letras de$A = \{a, b, c, d\}\text{?}$ Tenga en cuenta aquí que no nos preocupa el orden de las tres letras. Por ensayo y error, abc, abd, acd y bcd son los únicos listados posibles. Para repetir, estábamos buscando todos los subconjuntos de tres elementos del conjunto El$A\text{.}$ orden no es importante en los conjuntos. La notación para elegir 3 elementos de 4 es más común$\binom{4}{3}$ u ocasionalmente$C(4,3)\text{,}$ cualquiera de los cuales se lee “4 elige 3” o el número de combinaciones para cuatro objetos tomados tres a la vez.

Definición $\PageIndex{1}$: Binomial Coefficient

Dejar$n$ y$k$ ser enteros no negativos. El coeficiente binomial$\binom{n}{k}$ representa el número de combinaciones de$n$ objetos tomados$k$ a la vez, y se lee “$n$elegir$k\text{.}$”

Ahora nos gustaría investigar la relación entre los problemas de permutación y combinación para derivar una fórmula para$\binom{n}{k}$

Reconsideremos el Conteo sin Orden, Ejemplo$\PageIndex{2}$. Existen$3 ! = 6$ diferentes ordenamientos para cada uno de los subconjuntos de tres elementos. La siguiente tabla enumera cada subconjunto$A$ y todas las permutaciones de cada subconjunto en la misma línea.

\ begin {ecuación*}\ begin {array} {cc}\ textrm {subconjunto} &\ textrm {permutaciones}\\\ {a, b, c\} & abc, acb, bca, bac, cab, cba\\ {a, b, d\} & abd, adb, bda, bad, dab, dba\\\ {a, c, d\} & acd, adc, cda, cad, dac, dca\\ {b, c, d\} & bcd, bdc, cdb, cbd, dbc, dcb\\ end {array}\ text {.} \ end {ecuación*}

Por lo tanto,$\binom{4}{3} = \frac{P(4,3)}{3!} = \frac{4!}{(4-3)! \cdot 3!} = 4$

Generalizamos este resultado en el siguiente teorema:

Teorema$\PageIndex{1}$: Binomial Coefficient Formula

Si$n$ y$k$ son enteros no negativos con$0 \leq k \leq n\text{,}$ entonces el número$k$ -elemento subconjuntos de un conjunto de$n$ elementos es igual a

\ comenzar {ecuación*}\ binom {n} {k} =\ frac {n!} {(n-k)! \ cdot k!} \ texto {.} \ end {ecuación*}

Prueba

Prueba 1: Hay$k!$ formas de ordenar los elementos de cualquier conjunto de$k$ elementos. Por lo tanto,

\ begin {ecuación*}\ binom {n} {k} =\ frac {P (n, k)} {k!} =\ frac {n!} {(n-k)! k!}. \ texto {.} \ end {ecuación*}

Prueba 2: Para “construir” una permutación de$k$ objetos a partir de un conjunto de$n$ elementos, primero podemos elegir uno de los subconjuntos de objetos y, en segundo lugar, elegir una de las$k!$ permutaciones de esos objetos. Por regla de los productos,

\ comenzar {ecuación*} P (n, k) =\ binom {n} {k}\ cdot k! \ end {ecuación*}

y resolviendo para$\binom{n}{k}$ conseguimos la fórmula deseada.

Ejemplo$\PageIndex{3}$: Flipping Coins

Supongamos que una moneda equilibrada uniformemente se arroja cinco veces. ¿De cuántas formas se pueden obtener tres cabezas? Este es un problema de combinación, porque el orden en que aparecen las cabezas no importa. Podemos pensar en esto como una situación que involucra conjuntos al considerar el juego de volteretas de la moneda, del 1 al 5, en el que surgen cabezas. El número de formas de obtener tres cabezas es$\binom{5}{3}= \frac{5 \cdot 4}{2 \cdot 1} = 10\text{.}$

Ejemplo$\PageIndex{4}$: Counting Five Ordered Flips Two Ways

Determinamos el número total de formas ordenadas que una moneda justa puede aterrizar si se lanza cinco veces consecutivas. Los cinco lanzamientos pueden producir cualquiera de los siguientes eventos mutuamente excluyentes y disjuntos: 5 cabezas, 4 cabezas, 3 cabezas, 2 cabezas, 1 cabeza o 0 cabezas. Por ejemplo, por el ejemplo anterior, hay$\binom{5}{3}=10$ secuencias en las que aparecen tres cabezas. Contando las otras posibilidades de la misma manera, por la ley de adición tenemos:

\ begin {ecuación*}\ binom {5} {5} +\ binom {5} {4} +\ binom {5} {3} +\ binom {5} {2} +\ binom {5} {1} +\ binom {5} {0} = 1 + 5 +10+5+1 = 32\ fin {ecuación*}

formas de observar las cinco volteretas.

Por supuesto, también podríamos haber aplicado la regla extendida de los productos, y como hay dos posibles resultados para cada uno de los cinco tirados, tenemos$2^5 = 32$ formas.

Se podría pensar que contar algo de dos maneras es una pérdida de tiempo, pero resolver un problema de dos maneras diferentes a menudo es instructivo y conduce a valiosos conocimientos. En este caso, sugiere una fórmula general para la suma$\sum_{k=0}^n \binom{n}{k}\text{.}$ En el caso de$2^5$ que$n = 5\text{,}$ obtenemos por lo que es razonable esperar que la suma general es$2^n\text{,}$ y lo es. Un argumento lógico para probar el enunciado general consiste simplemente en generalizar el ejemplo anterior a volteretas de$n$ monedas.

Ejemplo$\PageIndex{5}$: A Committee of Five

Un comité generalmente comienza como un conjunto desestructurado de personas seleccionadas de una membresía más grande. Por lo tanto, un comité puede pensarse como una combinación. Si un club de 25 miembros tiene un comité social de cinco miembros, existen$\binom{25}{5}=\frac{25\cdot 24\cdot 23\cdot 22\cdot 21}{5!} = 53130$ diferentes comités sociales posibles. Si se pone alguna estructura o restricción en la forma en que se va a seleccionar el comité social, probablemente cambiará el número de comités posibles. Por ejemplo, si el club tiene una regla de que el tesorero debe estar en el comité social, entonces el número de posibilidades se reduce a$\binom{24}{4}=\frac{24\cdot 23\cdot 22\cdot 21}{4!} = 10626\text{.}$

Si además requerimos que un presidente distinto al tesorero sea seleccionado para el comité social, tenemos$\binom{24}{4} \cdot 4 = 42504$ diferentes comités sociales posibles. La elección de los cuatro no tesoreros explica el factor$\binom{24}{4}$ mientras que la necesidad de elegir un presidente representa el 4.

Ejemplo$\PageIndex{6}$: Binomial Coefficients - Extreme Cases

Simplemente aplicando la definición de un Coeficiente Binomial$\PageIndex{1}$, Definición, como una serie de subconjuntos vemos que hay$\binom{n}{0} = 1$ manera de elegir una combinación de cero elementos de un conjunto de$n\text{.}$ Además, vemos que hay$\binom{n}{n} = 1$ manera de elegir una combinación de$n$ elementos de un conjunto de$n\text{.}$

Podríamos calcular estos valores usando la fórmula que hemos desarrollado, pero aquí no se necesita realmente aritmética. Otras propiedades de los coeficientes binomiales que se pueden derivar usando la definición de subconjunto se verán en los ejercicios

Teorema binomial

El teorema binomial nos da una fórmula para expandir$( x + y )^{n}\text{,}$ donde$n$ es un entero no negativo. Los coeficientes de esta expansión son precisamente los coeficientes binomiales que hemos utilizado para contar combinaciones. Usando álgebra de secundaria podemos expandir la expresión para enteros de 0 a 5:

\ begin {ecuación*}\ begin {array} {cc} n & (x + y) ^n\\ 0 & 1\\ 1 & x+y\\ 2 & x^2+2 x y+y^2\\ 3 & x^3+3 x^2 y+3 x y+3 x y^2+y^3\\ 4 & x^4+4 x^3 y+6 x^3 y^2+4 x y^3 y^2+4 x y+6 x^3 y^2+4 x y^3 y^2+4 x y^3 y^y^4\\ 5 y x^5+5 x^4 y+10 x^3 y^2+10 x^2 y^3+5 x y^4+y^5\\ end {array}\ end {ecuación*}

En la expansión de$(x + y)^{5}$ notamos que el coeficiente del tercer término es$\binom{5}{3} = 10\text{,}$ y el del sexto término es$\binom{5}{5}=1\text{.}$ Podemos reescribir la expansión como

\ begin {ecuación*}\ binom {5} {0} x^5+\ binom {5} {1} x^4 y+\ binom {5} {2} x^3 y^2+\ binom {5} {3} x^2 y^3+\ binom {5} {4} x y^4+\ binom {5} {5} y^5\ texto {.} \ end {ecuación*}

En resumen, en la ampliación de$( x + y )^{n}$ señalamos:

1. El primer término es$x^n$ y el último término es$y^n\text{.}$
2. Con cada término sucesivo, exponentes de$x$ disminución en 1 como los de$y$ incremento en 1. Para cualquier término la suma de los exponentes es$n\text{.}$
3. El coeficiente de$x^{n-k} y^k$ es$\binom{n}{k}\text{.}$
4. La matriz triangular de coeficientes binomiales se llama triángulo de Pascal después del matemático francés del siglo XVII Blaise Pascal. Tenga en cuenta que cada número en el triángulo distinto de los 1 en los extremos de cada fila es la suma de los dos números a la derecha e izquierda del mismo en la fila de arriba.

Teorema$\PageIndex{2}$: The Binomial Theorem

Si$n \geq 0\text{,}$ y$x$ y$y$ son números, entonces

\ begin {ecuación*} (x+y) ^ {n} =\ suma_ {k=0} ^n\ binom {n} {k} x^ {n-k} y^k\ text {.} \ end {ecuación*}

Prueba

Este teorema se probará mediante un procedimiento lógico denominado inducción matemática, que se introducirá en el Capítulo 3.

Ejemplo$\PageIndex{7}$: Identifying a Term in an Expansion

Encuentra el tercer término en la expansión de$(x-y)^{4} = (x+(-y))^{4}\text{.}$ El tercer término, cuando$k=2\text{,}$ es$\binom{4}{2} x^{4-2} (-y)^2 = 6 x^2 y^2\text{.}$

Ejemplo$\PageIndex{8}$: A Binomial Expansion

Expandir$(3 x - 2 )^{3}\text{.}$ Si reemplazamos$x$ y$y$ en el Teorema Binomial con$3x$ y$-2\text{,}$ respectivamente, obtenemos

\ begin {ecuación*}\ begin {split}\ sum_ {k=0} ^3\ binom {3} {k} (3x) ^ {n-k} (-2) ^k & =\ binom {3} {0} (3x) ^ {3} (-2) ^0 +\ binom {3} {1} (3x) ^ {2} (-2) ^1 +\ binom {3} {2} (3x) ^ {1} (-2) ^2 +\ binom {3} {3} (3x) ^ {0} (-2) ^3\\ & = 27 x^3 - 54 x^2 + 36 x - 8\ end {split}\ text {.} \ end {ecuación*}

Nota de Sage Math

Una mano de puente es un subconjunto de 13 elementos de una baraja estándar de 52 cartas. El orden en que las cartas lleguen al jugador no importa. Desde el punto de vista de un solo jugador, el número de manos de puente posibles es el$\binom{52}{13}\text{,}$ que se puede calcular fácilmente con$Sage\text{.}$

view sourceprint?

1	binomial(52,13)

En bridge, la ubicación de una mano en relación con el crupier tiene alguna incidencia en el juego. Una indicación aún más verdadera del número de manos posibles toma en cuenta la mano posible del$each$ jugador. Es costumbre referirse a las posiciones de los puentes como Oeste, Norte, Este y Sur. Podemos aplicar la regla de producto para obtener el número total de manecillas de puente con la siguiente lógica. Oeste puede obtener cualquiera de las$\binom{52}{13}$ manos identificadas anteriormente. Entonces Norte consigue 13 de las 39 tarjetas restantes y así tiene manos$\binom{39}{13}$ posibles. Oriente entonces obtiene 13 de las 26 cartas restantes, lo que tiene$\binom{26}{13}$ posibilidades. Sur obtiene las cartas restantes. Por lo tanto, el número de manecillas de puente se calcula utilizando la Regla de Producto

view sourceprint?

1	binomial(52,13)*binomial(39,13)*binomial(26,13)

Ejercicios

Ejercicio$\PageIndex{1}$

El comité judicial de un colegio está integrado por tres profesores y cuatro estudiantes. Si diez profesores y 25 estudiantes han sido nominados para el comité, ¿cuántos comités judiciales podrían formarse en este momento?

Contestar

$\binom{10}{3}\cdot \binom{25}{4}=1,518,000$

Ejercicio$\PageIndex{2}$

Supongamos que un solo carácter se almacena en una computadora usando ocho bits.

1. ¿Cuántos patrones de bits tienen exactamente tres 1's?
2. ¿Cuántos patrones de bits tienen al menos dos 1's?

Pista

Piense en el conjunto de posiciones que contienen un 1 para convertir esto es en una pregunta sobre conjuntos.

Contestar

1. $\binom{8}{3}$
2. $2^8-(\binom{8}{0}+\binom{8}{1})$

Ejercicio$\PageIndex{3}$

¿Cuántos subconjuntos de$\{1, 2, 3, \dots , 10\}$ contienen al menos siete elementos?

Contestar

$\binom{10}{7} +\binom{10}{8} +\binom{10}{9} +\binom{10}{10}= 120+45+10+1=176$

Ejercicio$\PageIndex{4}$

Las comisiones congresionales de matemáticas e informática están integradas por cinco representantes cada una, y una norma congresional es que las dos comisiones deben ser disjuntas. Si hay 385 miembros del Congreso, ¿de cuántas formas podrían seleccionarse los comités?

Ejercicio$\PageIndex{5}$

La imagen de abajo muestra una cuadrícula de 6 por 6 y un ejemplo de un camino de celosía que podría tomarse desde el$(6,6)\text{,}$ cual es un camino tomado viajando$(0,0)$ a lo largo de líneas de cuadrícula que van solo hacia la derecha y hacia arriba. ¿Cuántos caminos de celosía diferentes hay de este tipo? Generalizar al caso de rutas de celosía de$(0,0)$ a$(m,n)$ para cualquier número entero no negativo$m$ y$n\text{.}$

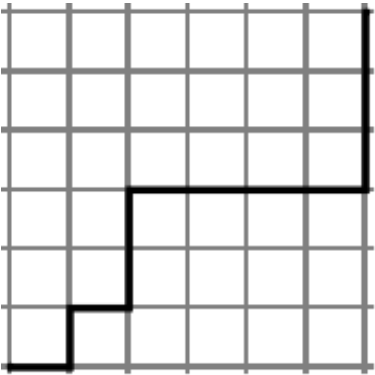
Figura$\PageIndex{1}$: Una trayectoria de celosía

 

Pista

Piense en cada camino como una secuencia de instrucciones para ir a la derecha (R) y subir (U).

Contestar

Cada ruta puede describirse como una secuencia o R y U con exactamente seis de cada una. Las seis posiciones en las que se podrían colocar las R's se pueden seleccionar de las doce posiciones en las$\binom{12}{6}$ formas de secuencia. Podemos generalizar esta lógica y ver que hay$\binom{m+n}{m}$ caminos desde$(0,0)$ hasta$(m,n)\text{.}$

Ejercicio$\PageIndex{6}$

¿Cuántos de los caminos de celosía de$(6,6)$ pasar$(0,0)$ a través$(3,3)$ como lo$\PageIndex{1}$ hace el de la Figura?

Ejercicio$\PageIndex{7}$

Un juego de póquer se juega con 52 cartas. Al inicio de un juego, cada jugador obtiene cinco de las cartas. El orden en que se reparten las cartas no importa.

1. ¿Cuántas “manos” de cinco cartas son posibles?
2. Si hay cuatro personas jugando, ¿cuántas “manos” iniciales de cinco cartas son posibles, tomando en cuenta a todos los jugadores y sus posiciones en la mesa? La posición con respecto al distribuidor sí importa.

Contestar

1. $\displaystyle C(52,5)=2,598,960$
2. $\displaystyle \binom{52}{5}\cdot \binom{47}{5}\cdot \binom{42}{5}\cdot \binom{37}{5}$

Ejercicio$\PageIndex{8}$

Un rubor en una mano de póquer de cinco cartas son cinco cartas del mismo palo. Los trajes son espadas, palos, diamantes y corazones. ¿Cuántas descargas de pala son posibles en una baraja de 52 cartas? ¿Cuántos sofocos son posibles en cualquier traje?

Ejercicio$\PageIndex{9}$

¿Cuántas manos de póquer de cinco cartas que usan 52 cartas contienen exactamente dos ases?

Contestar

$\binom{4}{2} \cdot \binom{48}{3} = 6 \cdot 17296=103776$

Ejercicio$\PageIndex{10}$

En el póquer, una casa llena es de tres en su tipo y una pareja en una mano; por ejemplo, tres cincos y dos reinas. ¿Cuántas casas llenas son posibles de una baraja de 52 cartas? Puedes usar la celda sage en la Nota de SaeMath para hacer este cálculo, pero también escribir tu respuesta en términos de coeficientes binomiales.

Ejercicio$\PageIndex{11}$

Una clase de doce estudiantes de informática se dividirá en tres grupos de 3, 4 y 5 estudiantes para trabajar en un proyecto. ¿De cuántas maneras se puede hacer esto si cada estudiante va a estar exactamente en un grupo?

Contestar

$\binom{12}{3}\cdot\binom{9}{4}\cdot\binom{5}{5}$

Ejercicio$\PageIndex{12}$

Explique en palabras por qué las siguientes igualdades son verdaderas en función del número de subconjuntos, y luego verificar las igualdades usando la fórmula para los coeficientes binomiales.

1. $\displaystyle \binom{n}{1} = n$
2. $\binom{n}{k} = \binom{n}{n-k}\text{,}$$0 \leq k \leq n$

Ejercicio$\PageIndex{13}$

Hay diez puntos,$P_1, P_2, \dots , P_{10}$ en un avión, no tres en la misma línea.

1. ¿Cuántas líneas están determinadas por los puntos?
2. ¿Cuántos triángulos están determinados por los puntos?

Contestar

1. $\displaystyle \binom{10}{2}=45$
2. $\displaystyle \binom{10}{3}=120$

Ejercicio$\PageIndex{14}$

¿De cuántas maneras se pueden agrupar$n$ las personas en parejas cuando$n$ es par? Asumir el orden de los pares importa, pero no el orden dentro de los pares. Por ejemplo, si$n=4\text{,}$ las seis agrupaciones diferentes serían

\ begin {ecuación*}\\ comenzar {array} {cc}\ {1,2\} &\ {3,4\}\\\ {1,3\} &\ {2,4\}\\ {1,4\} &\ {2,3\}\\ {2,3\} &\ {1,4\}\\ {2,4\} &\ {1,3\} &\ {1,3\}\\ {3,4\} &\ {1,2\} end {array}\ end {ecuación*}

Ejercicio$\PageIndex{15}$

Usa el teorema binomial para probar que si$A$ es un conjunto finito, entonces$\lvert P(A)\rvert =2^{\lvert A \rvert}$

Contestar

Asumir$\lvert A \rvert =n\text{.}$ Si dejamos$x=y=1$ entrar el Teorema Binomial, obtenemos$2^n=\binom{n}{0}+\binom{n}{1}+\cdots +\binom{n}{n}\text{,}$ con el lado derecho de la igualdad contando todos los subconjuntos de$0, 1, 2, \dots , n$ elementos$A$ que contienen. De ahí$\lvert P(A)\rvert =2^{\lvert A \rvert}$

Ejercicio$\PageIndex{16}$

1. La lotería de un estado implica elegir seis números diferentes de un posible 36. ¿De cuántas maneras puede una persona elegir seis números?
2. ¿Cuál es la probabilidad de que una persona gane con una apuesta?

Ejercicio$\PageIndex{17}$

Usar el teorema binomial para calcular$9998^3\text{.}$

Pista

$9998 = 10000-2$

Contestar

$10000^3 - 3 \cdot 2 \cdot 10000^2 +3 \cdot 2^2 \cdot 10000 - 2^3 = 999,400,119,992.$

Ejercicio$\PageIndex{18}$

En el juego de cartas Blackjack, hay uno o más jugadores y un crupier. Inicialmente, a cada jugador se le reparten dos cartas y al crupier se le reparte una carta hacia abajo y una hacia arriba. Como en bridge, el orden de las manos, pero no el orden de las cartas en las manos, importa. Comenzando con una sola baraja de 52 cartas, y tres jugadores, ¿de cuántas formas se pueden repartir las dos primeras cartas? Puedes usar la celda de sabio en la Nota de SageMath para hacer este cálculo.