4.1: Métodos de Prueba para Conjuntos

Si\(A\text{,}\)\(B\text{,}\) y\(C\) son conjuntos arbitrarios, es siempre cierto que\(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\text{?}\) Hay una variedad de formas en las que podríamos intentar probar que esta ley distributiva para intersección sobre unión es efectivamente cierta. Comenzamos con una “no prueba” común y luego trabajamos hacia métodos más aceptables.

Ejemplos y Contraejemplos

Podríamos, por ejemplo, dejar\(A = \{1, 2\}\text{,}\)\(B = \{5, 8, 10\}\text{,}\)\(C = \{3, 2, 5\}\text{,}\) y determinar si la ley distributiva es cierta para estos valores de\(A\text{,}\)\(B\text{,}\) y\(C\text{.}\) Al hacer esto solo habremos determinado que la ley distributiva es cierta para este ejemplo. No prueba la ley distributiva para todos los conjuntos posibles\(A\text{,}\)\(B\text{,}\)\(C\) y por lo tanto es un método de prueba inválido. No obstante, probar algunos ejemplos tiene un mérito considerable en la medida en que nos hace sentir más cómodos con la afirmación en cuestión. En efecto, si la afirmación no es cierta para el ejemplo, la hemos desmentido.

Definición\(\PageIndex{1}\): Counterexample

Un ejemplo que desmiente una declaración se llama contraejemplo.

Ejemplo\(\PageIndex{1}\): Disproving Distributivity of Addition over Multiplication

Del álgebra básica aprendimos que la multiplicación es distributiva sobre la suma. ¿La suma es distributiva sobre la multiplicación? Es decir, ¿\(a + (b \cdot c) = (a + b) \cdot (a + c)\)siempre es cierto? Si elegimos los valores\(a = 3\text{,}\)\(b = 4\text{,}\) y\(c = 1\text{,}\) encontramos que\(3 + (4 \cdot 1) \neq (3 + 4)\cdot (3 + 1)\text{.}\) Por lo tanto, este conjunto de valores sirve como contraejemplo a una ley distributiva de suma sobre multiplicación.

Prueba usando diagramas de Venn

En este método, ilustramos ambos lados de la declaración a través de un diagrama de Venn y determinamos si ambos diagramas de Venn nos dan la misma “imagen”, Por ejemplo, el lado izquierdo de la ley distributiva se desarrolla en Figura\(\PageIndex{1}\) y el lado derecho en Figura\(\PageIndex{2}\). Tenga en cuenta que los resultados finales le dan la misma área sombreada.

La ventaja de este método es que es relativamente rápido y mecánico. La desventaja es que solo es viable si hay un pequeño número de conjuntos bajo consideración. Además, no funciona muy bien en un entorno estático como un libro o papel de prueba. Los diagramas de Venn suelen funcionar bien si tienes un entorno potencialmente dinámico como una pizarra o un video.

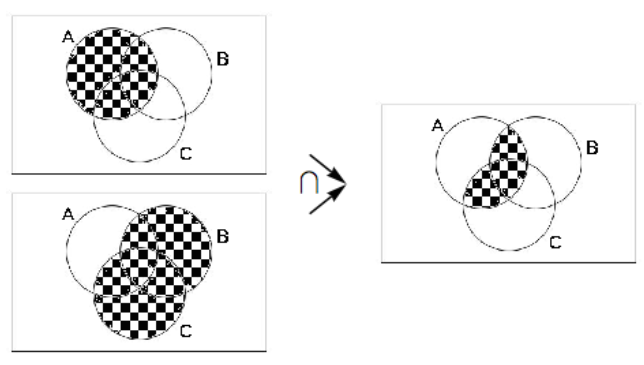Figura\(\PageIndex{1}\): Desarrollo del lado izquierdo de la ley distributiva para conjuntos.

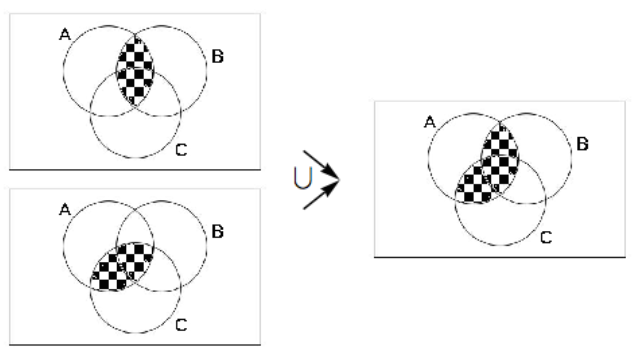Figura\(\PageIndex{2}\): Desarrollo del lado derecho de la ley distributiva para conjuntos

Prueba usando tablas Set-membresías

Dejar\(A\) ser un subconjunto de un conjunto universal\(U\) y dejar\(u\in U\text{.}\) Para usar este método observamos que exactamente uno de los siguientes es cierto:\(u \in A\) o\(u\notin A\text{.}\) Denotar la situación donde\(u \in A\) por 1 y aquella donde\(u \notin A\) por 0. Trabajar con dos conjuntos,\(A\)\(B\text{,}\) y si\(u \in U\text{,}\) hay cuatro posibles resultados de “dónde\(u\) puede estar”. ¿Qué son? La tabla de conjunto de miembros para\(A \cup B\) es:

Tabla\(\PageIndex{1}\): Mesa de Membresía para\(A\cup B\)

\(A\)	\(B\)	\(A\cup B\)
\ (A\) ">\(0\)	\ (B\) ">\(0\)	\ (A\ taza B\) ">\(0\)
\ (A\) ">\(0\)	\ (B\) ">\(1\)	\ (A\ taza B\) ">\(1\)
\ (A\) ">\(1\)	\ (B\) ">\(0\)	\ (A\ taza B\) ">\(1\)
\ (A\) ">\(1\)	\ (B\) ">\(1\)	\ (A\ taza B\) ">\(1\)

Esta tabla ilustra que\(u\in A \cup B\) si y solo si\(u\in A\) o\(u \in B\text{.}\)

Para probar la ley distributiva a través de una tabla set-membership, escriba la tabla para cada lado de la sentencia set a probar y anote que si\(S\) y\(T\) son dos columnas en una tabla, entonces la sentencia set\(S\) es igual a la sentencia set\(T\) si y solo si corresponde las entradas en cada fila son las mismas.

Para probar\(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\text{,}\) primero señalar que el enunciado involucra tres conjuntos,\(A\text{,}\)\(B\text{,}\) y\(C\text{,}\) así hay\(2^3= 8\) posibilidades para la pertenencia de un elemento en los conjuntos.

Tabla\(\PageIndex{2}\): Mesa de afiliación para acreditar la ley distributiva de intersección sobre sindicato

\(A\)	\(B\)	\(C\)	\(B\cup C\)	\(A\cap B\)	\(A\cap C\)	\(A\cap (B\cup C)\)	\((A\cap B)\cup (A\cap C)\)
\ (A\) ">\(0\)	\ (B\) ">\(0\)	\ (C\) ">\(0\)	\ (B\ taza C\) ">\(0\)	\ (A\ cap B\) ">\(0\)	\ (A\ cap C\) ">\(0\)	\ (A\ gorra (B\ copa C)\) ">\(0\)	\ ((A\ cap B)\ copa (A\ cap C)\) ">\(0\)
\ (A\) ">\(0\)	\ (B\) ">\(0\)	\ (C\) ">\(1\)	\ (B\ taza C\) ">\(1\)	\ (A\ cap B\) ">\(0\)	\ (A\ cap C\) ">\(0\)	\ (A\ gorra (B\ copa C)\) ">\(0\)	\ ((A\ cap B)\ copa (A\ cap C)\) ">\(0\)
\ (A\) ">\(0\)	\ (B\) ">\(1\)	\ (C\) ">\(0\)	\ (B\ taza C\) ">\(1\)	\ (A\ cap B\) ">\(0\)	\ (A\ cap C\) ">\(0\)	\ (A\ gorra (B\ copa C)\) ">\(0\)	\ ((A\ cap B)\ copa (A\ cap C)\) ">\(0\)
\ (A\) ">\(0\)	\ (B\) ">\(1\)	\ (C\) ">\(1\)	\ (B\ taza C\) ">\(1\)	\ (A\ cap B\) ">\(0\)	\ (A\ cap C\) ">\(0\)	\ (A\ gorra (B\ copa C)\) ">\(0\)	\ ((A\ cap B)\ copa (A\ cap C)\) ">\(0\)
\ (A\) ">\(1\)	\ (B\) ">\(0\)	\ (C\) ">\(0\)	\ (B\ taza C\) ">\(0\)	\ (A\ cap B\) ">\(0\)	\ (A\ cap C\) ">\(0\)	\ (A\ gorra (B\ copa C)\) ">\(0\)	\ ((A\ cap B)\ copa (A\ cap C)\) ">\(0\)
\ (A\) ">\(1\)	\ (B\) ">\(0\)	\ (C\) ">\(1\)	\ (B\ taza C\) ">\(1\)	\ (A\ cap B\) ">\(0\)	\ (A\ cap C\) ">\(1\)	\ (A\ gorra (B\ copa C)\) ">\(1\)	\ ((A\ cap B)\ copa (A\ cap C)\) ">\(1\)
\ (A\) ">\(1\)	\ (B\) ">\(1\)	\ (C\) ">\(0\)	\ (B\ taza C\) ">\(1\)	\ (A\ cap B\) ">\(1\)	\ (A\ cap C\) ">\(0\)	\ (A\ gorra (B\ copa C)\) ">\(1\)	\ ((A\ cap B)\ copa (A\ cap C)\) ">\(1\)
\ (A\) ">\(1\)	\ (B\) ">\(1\)	\ (C\) ">\(1\)	\ (B\ taza C\) ">\(1\)	\ (A\ cap B\) ">\(1\)	\ (A\ cap C\) ">\(1\)	\ (A\ gorra (B\ copa C)\) ">\(1\)	\ ((A\ cap B)\ copa (A\ cap C)\) ">\(1\)

Dado que cada entrada en la Columna 7 es la misma que la entrada correspondiente en la Columna 8, hemos demostrado que\(A\cap (B \cup C) = (A\cap B) \cup (A \cap C)\) para cualquier conjunto\(A\text{,}\)\(B\text{,}\) y\(C\text{.}\) La principal ventaja de este método es que es mecánico. La principal desventaja es que es razonable usar solo para un número relativamente pequeño de conjuntos. Si estamos tratando de probar una declaración que involucra cinco conjuntos, hay\(2^5 = 32\) filas, lo que pondría a prueba la paciencia de cualquiera haciendo el trabajo a mano.

Prueba usando definiciones

Este método implica el uso de definiciones y conceptos básicos para probar la afirmación dada. Este procedimiento obliga a uno a aprender, volver a aprender y comprender definiciones y conceptos básicos. Ayuda a los individuos a enfocar su atención en las ideas principales de cada tema y por lo tanto es el método de prueba más útil. Uno no aprende un tema memorizando u ocasionalmente mirando temas centrales, sino usándolos en una variedad de contextos. La palabra prueba entra en pánico a la mayoría de la gente; sin embargo, todos pueden sentirse cómodos con las pruebas. No esperes probar cada declaración de inmediato. De hecho, no es nuestro propósito probar cada teorema o hecho encontrado, solo aquellos que ilustran métodos y/o conceptos básicos. A lo largo del texto nos centraremos en las principales técnicas de pruebas. Ilustremos probando la ley distributiva.

Técnica de Prueba 1. Afirma o reformula el teorema para que entiendas lo que se da (la hipótesis) y lo que estás tratando de probar (la conclusión).

Teorema\(\PageIndex{1}\): The Distributive Law of Intersection over Union

Si\(A\text{,}\)\(B\text{,}\) y\(C\) son conjuntos, entonces\(A\cap (B \cup C) = (A\cap B) \cup (A \cap C)\text{.}\)

Prueba

Lo que podemos suponer:\(A\text{,}\)\(B\text{,}\) y\(C\) son conjuntos.

Lo que vamos a demostrar:\(A\cap (B \cup C) = (A\cap B) \cup (A \cap C)\text{.}\)

Comentario: ¿Con qué tipos de objetos estoy trabajando: conjuntos? números reales? proposiciones? La respuesta son conjuntos: conjuntos de elementos que pueden ser cualquier cosa que te importe imaginar. El universo del que sacamos nuestros elementos no juega ningún papel en la prueba de este teorema.

Tenemos que demostrar que los dos conjuntos son iguales. Llamémoslos el conjunto de la izquierda\((LHS\)) y el conjunto de la derecha (\(RHS\)). Para probar que\(LHS = RHS\text{,}\) debemos probar dos cosas: (a)\(LHS\subseteq RHS\text{,}\) y (b)\(RHS \subseteq LHS\text{.}\)

Para probar la parte a y, de igual manera, la parte b, debemos demostrar que cada elemento de\(LHS\) es un elemento de\(RHS\text{.}\) Una vez que hayamos diagnosticado el problema estamos listos para comenzar.

Debemos demostrar: a\(A \cap (B \cup C)\subseteq (A\cap B) \cup (A\cap C)\text{.}\)

Let\(x \in A\cap (B \cup C)\text{:}\)

\ begin {ecuation*}\ begin {split} x\ in A\ cap (B\ cup C) &\ Rightarrow x\ in A\ textrm {y} (x\ in B\ textrm {o} x\ en C)\\ &\ quad\ textrm {def. de unión e intersección}\\ &\ Rightarrow (x\ in A\ textrm {y}\ en B)\ textrm {o} (x\ en A\ textrm {y} x\ en C)\\ &\ quad\ textrm {ley distributiva de lógica}\\ &\ Rightarrow (x\ in A\ cap B)\ textrm {or} (x\ in A\ cap C)\\ &\ quad\ textrm {def. de intersección}\\ &\ Rightarrow x\ in (A\ cap B)\ copa (A\ cap C)\\ &\ quad\ textrm {def. de unión}\ end {split}\ fin {ecuación*}

También debemos probar (b)\((A\cap B) \cup (A\cap C)\subseteq A \cap (B \cup C)\text{.}\)

\ begin {equation*}\ begin {split} x\ in (A\ cap B)\ cup (A\ cap C) &\ Rightarrow (x\ in A\ cap B)\ text {or} (x\ in A\ cap C)\\ &\ quad\ textrm {¿Por qué? }\\ &\ Rightarrow (x\ en A\ textrm {y} x\ en B)\ textrm {o} (x\ en A\ textrm {y} x\ en C)\\\ &\ quad\ textrm {¿Por qué? }\\ &\ Rightarrow x\ en A\ textrm {y} (x\ en B\ textrm {o} x\ en C)\\ &\ quad\ textrm {¿Por qué? }\\ &\ Rightarrow x\ in A\ cap (B\ copa C)\\ &\ quad\ textrm {¿Por qué? }\ cuadrado\ final {dividir}\ texto {.} \ end {ecuación*}

Prueba T echnique 2

1. Para probar que\(A\subseteq B\text{,}\) debemos demostrar que si\(x \in A\text{,}\) entonces\(x \in B\text{.}\)
2. Para demostrar que\(A = B\text{,}\) debemos mostrar:
   1. \(A\subseteq B\)y
   2. \(B \subseteq A\text{.}\)

Para ilustrar mejor la técnica Prueba por definición, probemos el siguiente teorema.

Teorema\(\PageIndex{2}\): Another Proof using Definitions

Si\(A\text{,}\)\(B\text{,}\) y\(C\) son algunos conjuntos, entonces\(A \times (B \cap C) = (A \times B) \cap (A \times C)\text{.}\)

Prueba

Comentario; Nuevamente nos preguntamos: ¿Qué estamos tratando de probar? ¿Con qué tipos de objetos estamos tratando? Nos damos cuenta de que deseamos probar dos hechos: a\(LHS\subseteq RHS\text{,}\) yb\(RHS\subseteq LHS\text{.}\)

Para probar la parte (a), y de manera similar la parte (b), comenzaremos de la misma manera. Vamos\(\_\_\_ \in LHS\) a mostrar\(\_\_\_ \in RHS\text{.}\) ¿Qué debería\(\_\_\_\) ser? ¿Qué\(LHS\) aspecto tiene un objeto típico en el?

Ahora, a la prueba real.

1. \(A\times (B\cap C)\subseteq (A\times B)\cap (A\times C)\text{.}\)
   Vamos\((x, y) \in A\times (B\cap C)\text{.}\)
   \ comenzar {ecuación*}\ comenzar {dividir} (x, y)\ en A\ veces (B\ cap C) &\ Rightarrow x\ en A\ textrm {y} y\ in (B\ cap C)\\ &\ quad\ textrm {¿Por qué? }\\ &\ Rightarrow x\ en A\ textrm {y} (y\ en B\ textrm {y} y\ en C)\\ &\ textrm {¿Por qué? }\\ &\ Rightarrow (x\ en A\ textrm {y} y\ en B)\ textrm {y} (x\ en A\ textrm {y} y\ en C)\\\ &\ quad\ textrm {¿Por qué? }\\ &\ Rightarrow (x, y)\ in (A\ times B)\ textrm {y} (x, y)\ in (A\ times C)\\ &\ quad\ textrm {¿Por qué? }\\ &\ Rightarrow (x, y)\ in (A\ times B)\ cap (A\ times C)\\ &\ quad\ textrm {¿Por qué? }\ end {split}\ end {ecuación*}
2. \((A\times B)\cap (A\times C)\subseteq A\times ( B\cap C)\text{.}\)
   Vamos\((x, y) \in (A\times B) \cap (A\times C)\text{.}\)
   \ comenzar {ecuación*}\ comenzar {dividir} (x, y)\ in (A\ veces B)\ cap (A\ veces C) &\ Rightarrow (x, y)\ in A\ veces B\ textrm {y} (x, y)\ en A\ veces C\\ &\ quad\ textrm {¿Por qué? }\\ &\ Rightarrow (x\ en A\ textrm {y} y\ en B)\ textrm {y} (x\ en A\ textrm {y} y\ en C)\\\ &\ quad\ textrm {¿Por qué? }\\ &\ Rightarrow x\ en A\ textrm {y} (y\ en B\ textrm {y} y\ en C)\\ &\ quad\ textrm {¿Por qué? }\\ &\ Rightarrow x\ in A\ textrm {y} y\ in (B\ cap C)\\ &\ quad\ textrm {¿Por qué? }\\ &\ Rightarrow (x, y)\ in A\ times (B\ cap C)\\ &\ quad\ textrm {¿Por qué? }\ end {split}\ end {ecuación*}

Ejercicios

Ejercicio\(\PageIndex{1}\)

Demostrar lo siguiente:

1. Dejar\(A\text{,}\)\(B\text{,}\) y\(C\) ser conjuntos. Si\(A\subseteq B\) y\(B\subseteq C\text{,}\) entonces\(A\subseteq C\text{.}\)
2. Dejar\(A\) y\(B\) ser conjuntos. Entonces\(A - B= A\cap B^c\).
3. \(A,B, \textrm{ and } C\)Dejen ser conjuntos. Si (\(A\subseteq B\)y\(A\subseteq C\)) entonces\(A\subseteq B\cap C\text{.}\)
4. \(A \textrm{ and } B\)Dejen ser conjuntos. \(A\subseteq B\)si y sólo si\(B^c\subseteq A^c\).
5. \(A,B, \textrm{ and } C\)Dejen ser conjuntos. Si\(A\subseteq B\) entonces\(A\times C \subseteq B\times C\text{.}\)

Contestar

1. Supongamos que\(x\in A\) (condition of the conditional conclusion \(A \subseteq C\)). Since \(A \subseteq B\text{,}\) \(x\in B\) by the definition of \(\subseteq\text{.}\) \(B\subseteq C\) and \(x\in B\) implies that \(x\in C\text{.}\) Therefore, if \(x\in A\text{,}\) then \(x\in C\text{.}\) \(\square\)
2. (Prueba de que\(A -B \subseteq A\cap B^c\)) Let\(x\) be in\(A - B\text{.}\) Por lo tanto, x está adentro\(A\text{,}\) pero no está en B; es decir,\(\text{ }x \in A\) y\(x \in B^c \Rightarrow x\in A\cap B^c\text{.}\)\(\square\)
3. \((\Rightarrow )\)Asumir eso\(A \subseteq B\) y\(A \subseteq C\text{.}\) Dejar\(x\in A\text{.}\) Por las dos premisas,\(x\in B\) y\(x\in C\text{.}\) Por lo tanto, por la definición de intersección,\(x\in B\cap C\text{.}\)\(\square\)
4. \((\Rightarrow )\)(Indirecto) Supongamos que no\(B^c\) es un subconjunto de\(A^c\). Por lo tanto, existe\(x\in B^c\) que no pertenece a\(A^c\text{.}\)\(x \notin A^c \Rightarrow x \in A\text{.}\) Por lo tanto,\(x\in A\) y\(x\notin B\text{,}\) una contradicción con el supuesto de que\(A\subseteq B\text{.}\)\(\square\)
5. Hay dos casos a considerar. El primero es cuando\(C\) está vacío. Entonces sigue la conclusión ya que ambos productos cartesianos están vacíos.
   Si\(C\) no está vacío, tenemos dos subcasos, si\(A\) está vacío,\(A\times C = \emptyset\text{,}\) que es un subconjunto de cada conjunto. Por último, el subcaso interesante es cuando no\(A\) está vacío. Ahora elegimos cualquier par\((a,c) \in A\times C\text{.}\) Esto significa que\(a\) está en\(A\) y\(c\) está en\(C\text{.}\) Dado que\(A\) es un subconjunto de\(B\text{,}\)\(a\) está en\(B\) y así\((a,c) \in B \times C\text{.}\) Por lo tanto\(A\times C \subseteq B\times C\text{.}\)\(\square\)

Ejercicio\(\PageIndex{2}\)

Escribir lo contrario de las partes (a), (c) y (e) del Ejercicio 1 y probarlas o desacreditarlas.

Ejercicio\(\PageIndex{3}\)

Desmentir lo siguiente, asumiendo que\(A, B, \textrm{ and } C\) son conjuntos:

1. \(A - B = B - A\text{.}\)
2. \(A\times B = B\times A\text{.}\)
3. \(A \cap B = A \cap C\)implica\(B = C\text{.}\)
4. \(\displaystyle A \oplus (B\cap C) = (A \oplus B)\cap (A \oplus C)\)

Contestar

1. Si\(A = \mathbb{Z}\) y\(B=\emptyset\text{,}\)\(A - B = \pmb{\mathbb{Z}}\text{,}\) mientras\(B - A = \emptyset\text{.}\)
2. Si\(A=\{0\}\) y\(B = \{1\}\text{,}\)\((0,1) \in A \times B\text{,}\) pero no\((0, 1)\) está en\(B\times A\text{.}\)
3. Let\(A = \emptyset\text{,}\)\(B = \{0\}\text{,}\) y\(C = \{1\}\text{.}\)
4. Si\(A = \{1\}\text{,}\)\(B = \{1\}\text{,}\) y\(C =\emptyset\text{,}\) entonces el lado izquierdo de la identidad es\(\{1\}\) mientras que el lado derecho es el conjunto vacío. Otro ejemplo es\(A = \{1,2\}\text{,}\)\(B = \{1\}\text{,}\) y\(C =\{2\}.\)

Ejercicio\(\PageIndex{4}\)

\(A, B, \textrm{ and } C\)Dejen ser conjuntos. Escriba lo siguiente en “si.. entonces.” lenguaje y demuestre:

1. \(x \in B\)es una condición suficiente para\(x \in A \cup B\text{.}\)
2. \(A \cap B\cap C = \emptyset\)es una condición necesaria para\(A \cap B =\emptyset\text{.}\)
3. \(A \cup B = B\)es una condición necesaria y suficiente para\(A\subseteq B\text{.}\)

Ejercicio \(\PageIndex{5}\)

Demostrar por inducción que si\(A\text{,}\)\(B_1\text{,}\)\(B_2\text{,}\)...,\(B_n\) son conjuntos,\(n\geq 2\text{,}\) entonces\(A\cap ( B_1 \cup B_2\cup \dots \cup B_n) = (A \cap B_1) \cup (A \cap B_2 ) \cup \dots \cup (A\cap B_n)\text{.}\)

Contestar

Prueba: Let\(p(n)\) be

\ start {ecuación*} A\ gorra (B_1\ copa B_2\ taza\ cdots\ copa B_n) = (A\ gorra B_1)\ copa (A\ gorra B_2)\ copa\ cdots\ copa (A\ gorra B_n)\ texto {.} \ end {ecuación*}

Bases: Debemos demostrar que\(p(2) : A \cap (B_1 \cup B_2 )=(A\cap B_1) \cup (A\cap B_2)\) es verdad. Esto se hizo por varios métodos en la Sección 4.1.

Inducción: Asumir para algunos\(n\geq 2\) que\(p(n)\) es cierto. Entonces

\ begin {equation*}\ begin {split} A\ cap (B_1\ copa B_2\ taza\ cdots\ taza B_ {n+1}) &=A\ gorra ((B_1\ copa B_2\ taza\ cdots\ taza B_n)\ taza B_ {n+1})\\ &= (A\ cap (B_1\ taza B_2\ taza\ cdots taza\ cdots\ B_n))\ copa (A\ cap B_ {n+1})\ quad\ textrm {por} p (2)\\ &= ((A\ cap B_1)\ copa\ cdots\ copa (A\ cap B_n))\ copa (A\ cap B_ {n+1})\ quad\ textrm { por la hipótesis de inducción}\\ &= (A\ cap B_1)\ cup\ cdots\ cup (A\ cap B_n)\ cup (A\ cap B_ {n+1})\ quad\ square\\ end {split}\ end {equation*}

Ejercicio\(\PageIndex{6}\)

Dejar\(A\text{,}\)\(B\) y\(C\) ser conjuntos. Demostrar o desacreditar:

\ start {ecuación*} A\ cap B\ neq\ emptyset, B\ cap C\ neq\ emptyset\ fila derecha A\ cap C\ neq\ emptyset\ end {ecuación*}

Contestar

El enunciado es falso. Los conjuntos\(A=\{1,2\}\),\(B=\{2,3\}\) y\(C=\{3,4\}\) proporcionar un contraejemplo. De cara al Capítulo 6, diríamos que la relación de ser no disjuntos no es transitiva, Definición 6.3.3.