9.3: Conectividad

Última actualización
Guardar como PDF

Page ID: 117162

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Esta sección está dedicada a una pregunta que, al plantearse en relación con las gráficas que hemos examinado, parece trivial. Esa pregunta es: Dados dos vértices,$s$ y$t\text{,}$ de una gráfica, hay un camino de$s$ a$t\text{?}$ Si$s = t\text{,}$ esta pregunta se interpreta como preguntar si hay un circuito de longitud positiva comenzando en Por$s\text{.}$ supuesto, para las gráficas que hemos visto hasta ahora, esta pregunta pueden ser respondidas después de un breve examen.

Preliminares

Hay dos situaciones en las que una cuestión de este tipo no es trivial. Una es donde la gráfica es muy grande y un “examen” de la gráfica podría llevar una cantidad considerable de tiempo. Cualquiera que haya intentado resolver un laberinto puede haberse topado con un problema similar. La segunda situación interesante es cuando queremos plantearle la pregunta a una máquina. Si solo la información en los bordes entre los vértices es parte de la estructura de datos para la gráfica, ¿cómo puede juntar esa información para determinar si dos vértices se pueden conectar por una ruta?

Nota$\PageIndex{1}$: Connectivity Terminology

Dejar$v$ y$w$ ser vértices de una gráfica dirigida. Vertex$v$ está conectado a vértice$w$ si hay una ruta de$v$ a$w\text{.}$ Dos vértices están fuertemente conectados si están conectados en ambas direcciones entre sí. Un gráfico está conectado si, para cada par de vértices distintos,$v$ y$w\text{,}$$v$ está conectado$w$ o$w$ está conectado a$v\text{.}$ Un gráfico está fuertemente conectado si cada par de sus vértices está fuertemente conectado. Para una gráfica no dirigida, en la que los bordes se pueden usar en cualquier dirección, las nociones de fuertemente conectados y conectados son los mismos.

Teorema$\PageIndex{1}$: Maximal Path Theorem

Si una gráfica tiene$n$ vértices y el vértice$u$ está conectado al vértice$w\text{,}$, entonces existe una ruta de$u$ a$w$ de longitud no superior a$n\text{.}$

Prueba: (Indirecto): Supongamos que$u$ está conectado$w\text{,}$ pero la ruta más corta de$u$ a$w$ tiene longitud$m\text{,}$ donde$m>n\text{.}$ Una lista de vértices para una ruta de longitud$m$ tendrá$m + 1$ vértices. Este camino se puede representar como$\left(v_0,v_1,\ldots, v_m\right)\text{,}$ donde$v_0=u$ y$v_m= w\text{.}$ Tenga en cuenta que dado que solo hay$n$ vértices en la gráfica y$m$ los vértices se listan en el camino después$v_0\text{,}$ podemos aplicar el principio de encasillado y estar seguros de que debe haber alguna duplicación en el último $m$vértices de la lista de vértices, que representa un circuito en la ruta. Esto quiere decir que nuestro camino de longitud mínima se puede reducir, lo cual es una contradicción.

Método de matriz de adyacencia

Algorithm$\PageIndex{1}$: Adjacency Matrix Method

Supongamos que la información sobre los bordes en una gráfica se almacena en una matriz de adyacencia,$G\text{.}$ La relación,$r\text{,}$ que$G$ define es$v r w$ si hay un borde que se conecta$v$ a$w\text{.}$ Recordar que la composición de$r$ consigo misma,$r^2\text{,}$ se define por $v r^2 w$si existe un vértice$y$ tal que$v r y$ y es$y r w\text{;}$ decir,$v$ está conectado a$w$ por una trayectoria de longitud 2. Podríamos probar por inducción que la relación$r^k\text{,}$$k\geq 1\text{,}$ se define por$v r^k w$ si y solo si hay un camino de longitud$k$ desde$v$ hasta$w\text{.}$ Desde el cierre transitivo,$r^+\text{,}$ es la unión de$r\text{,}$$r^2$$,r^3,\ldots\text{,}$ podemos responder a nuestro cuestión de conectividad determinando el cierre transitivo del$r\text{,}$ cual se puede hacer más fácilmente manteniendo nuestra relación en forma de matriz. El teorema$\PageIndex{1}$ es significativo en nuestros cálculos porque nos dice que solo necesitamos ir tan lejos como$G^n$ para determinar la matriz del cierre transitivo.

La principal ventaja del método de matriz de adyacencia es que la matriz de cierre transitivo puede responder a todas las preguntas sobre la existencia de caminos entre cualquier vértice. Si$G^+$ es la matriz del cierre transitivo,$v_i$ está conectado a$v_j$ si y solo si$\left(G^+\right)_{i j }=1\text{.}$ Un grafo dirigido está conectado si$\left(G^+\right)_{i j }=1$ o$\left(G^+\right)_{j i}=1$ para cada$i\neq j\text{.}$ Una gráfica dirigida está fuertemente conectada si su matriz de cierre transitivo no tiene ceros.

Una desventaja del método de matriz de adyacencia es que la matriz de cierre transitivo nos dice si existe una ruta, pero no cuál es la ruta. El siguiente algoritmo resolverá este problema.

Búsqueda en primer lugar en la amplitud

Describiremos primero el Algoritmo de búsqueda de la amplitud primero con un ejemplo.

El equipo de futbol de la Universidad Estatal Mediocre (MSU) ha tenido un mal año, 2 victorias y 9 derrotas. Treinta días después del final de la temporada futbolística, los síndicos universitarios se reúnen para decidir si recontratar al entrenador en jefe; las cosas le quedan mal. No obstante, el día de la reunión, el entrenador emite el siguiente comunicado de prensa con resultados del año pasado:

Lista$\PageIndex{1}$: Press Release: MSU Completes Successful Season

El equipo de futbol de la Universidad Estatal Mediocre comparó favorablemente con el campeón nacional Enormous State University esta temporada.

Estado mediocre derrotó a Local A y M.
Local A y M derrotaron a City College.
City College derrotó a Corn State U.
... (25 resultados después)
Tough Tech derrotó a Enorme State University (ESU).

... ¡y ESU pasó a ganar el campeonato nacional!

¡Los síndicos quedaron tan impresionados que volvieron a contratar al entrenador con un aumento! ¿Cómo se le ocurrió al entrenador esa lista?

En realidad, tales listas existen ocasionalmente y han aparecido en los periódicos de vez en cuando. Por supuesto que realmente no prueban nada ya que cada equipo que derrotó a MSU en nuestro ejemplo anterior puede producir una cadena de resultados similar y más corta. Dado que los registros de fútbol universitario están fácilmente disponibles, el entrenador podría haber encontrado esta lista por ensayo y error. Todo lo que necesitaba para comenzar era que su equipo ganara al menos un juego. Desde que ESU perdió un juego, había cierta esperanza de producir la cadena.

El problema de encontrar esta lista equivale a encontrar un camino en la gráfica del torneo para la temporada futbolística del año pasado que inicia en MSU y termina en ESU. Tal gráfico está lejos de ser completo y es probable que se represente usando listas de bordes. Para que el problema del entrenador sea interesante, imaginemos que solo el ganador de cualquier juego recuerda el resultado del juego. El problema del entrenador ahora ha cobrado el sabor de un laberinto. Para llegar a ESU, debe comunicarse con los diversos equipos a lo largo del camino. Una forma en que el entrenador pudo haber descubierto su lista a tiempo es enviando los siguientes mensajes a los entrenadores de los dos equipos que MSU derrotó durante la temporada:

Nota$\PageIndex{2}$

Cuando se escribió este ejemplo por primera vez, comentamos que se deben ignorar los lazos. Las reglas más recientes de la NCAA piden un desempate en el fútbol universitario y así los lazos ya no son un problema. El correo electrónico tampoco era común y describimos el proceso en términos de cartas, no mensajes de correo electrónico. Otro cambio es que el entrenador también podría haber pedido al departamento de matemáticas de MSU que usara Mathematica o Sage para encontrar el camino!

Lista$\PageIndex{2}$: The Coach's Letter

Estimado entrenador de fútbol:

Por favor, siga estas instrucciones exactamente.

Si eres el entrenador en ESU, comunícate ahora con el entrenador de MSU y dile quién te envió este mensaje.
Si no eres el entrenador en ESU y este es el primer mensaje de este tipo que has recibido, entonces:
- Recuerda de quien recibiste este mensaje.
- Reenviar una copia de este mensaje, firmado por usted, a cada uno de los entrenadores cuyos equipos derrotaste durante el año pasado.
- Ignora este mensaje si ya has recibido uno como este.

$\quad \quad \quad \quad \quad $Firmado,

$\quad \quad \quad \quad \quad $Entrenador de MSU

Lista$\PageIndex{3}$: Observations

A partir de las condiciones de este mensaje, debe quedar claro que si todos cooperan y si los entrenadores participan dentro de un día de recibir el mensaje:

Si$n$ existe un camino de longitud de MSU a ESU, entonces el entrenador lo sabrá en$n$ días.
Al hacer una serie de llamadas telefónicas, el entrenador puede construir un camino que quiera llamando primero al entrenador que derrotó a ESU (la persona que envió ese mensaje al entrenador de ESU). Este entrenador sabrá quién le envió una carta, y así sucesivamente. Por lo tanto, la lista de vértices de la ruta deseada se construye en orden inverso.
Si se disputaron un total de partidos de$M$ fútbol, no se enviarán más de$M$ mensajes.
Si pasa un día sin que se envíe ningún mensaje, no existe ninguna ruta de MSU a ESU.
Este método podría ampliarse para construir una lista de todos los equipos a los que se puede conectar un equipo determinado. Simplemente imagina una serie de cartas como la anterior enviada por cada entrenador de fútbol y dirigidas a cualquier otro entrenador.

El problema general de encontrar un camino entre dos vértices en una gráfica, si existe uno, se puede resolver exactamente como resolvimos el problema anterior. El siguiente algoritmo, comúnmente llamado búsqueda en amplitud, usa una pila.

Nota$\PageIndex{3}$: Stacks

Una pila es una estructura de datos fundamental en la informática. Una analogía común utilizada para describir pilas es una pila de placas. Si pones un plato en la parte superior de una pila y luego quieres usar un plato, es natural usar ese plato superior. Entonces el último plato que entra es el primer plato que sale. “Último en entrar, primero en salir” es la breve descripción de la regla para pilas. Esto contrasta con una cola que utiliza una regla de “Primero en entrar, primero en salir”.

Algorithm$\PageIndex{2}$: Breadth-first Search

Un algoritmo de difusión para encontrar una ruta entre vértice$i$ y vértice$j$ de una gráfica que tiene$n$ vértices. Cada elemento$V_k$ de una lista$V=\left\{V_1, V_2, \ldots , V_n\right\}\text{,}$ consiste en un campo booleano$V_k.\text{found}$ y un campo entero$V_k.\text{from}\text{.}$ Los conjuntos$D_1\text{,}$$D_2, \dots\text{,}$ llamados conjuntos de profundidad, tienen la propiedad de que si$k \in D_r\text{,}$ entonces la ruta más corta de vértice$i$ a vértice$k$ es de longitud$r\text{.}$ En el paso 5 , se utiliza una pila para poner la lista de vértices para la ruta desde el vértice$i$ hasta el vértice$j$ en el orden adecuado. Esa pila es la salida del algoritmo.

Establecer el valor$V_k.\text{found}$ igual a False,$k = 1, 2, \dots , n$
$\displaystyle r = 0$
$\displaystyle D_0= \{i\}$
while$(\neg V_j.\text{found}$) y$\left(D_r\right.\neq \emptyset )$
- $\displaystyle D_{r+1}=\emptyset$
- por cada k adentro$D_r\text{:}$
  $\quad$ para cada borde (k, t):
  $\quad \quad $ Si$V_t.\text{found}$ == False:
  $\quad \quad \quad $$V_t.\text{found}=\text{True}$
  $\quad \quad \quad $$V_t.\text{from} = k$
  $\quad \quad \quad $$D_{r+1}=D_{r+1}\cup \{t\}$
- $\displaystyle r = r + 1$
si$V_j.\text{found}\text{:}$
- $\displaystyle S = Empty Stack$
- $\displaystyle k=j$
- mientras que$V_k.\text{from} \neq i\text{:}$
  $\quad$ Empuje$k$ sobre$S$
  $\quad$$k = V_k.\text{from}$
- Empuje$k$ sobre$S$
- Empuje$i$ sobre$S$

Lista$\PageIndex{4}$: Notes on Breadth-first Search

Este algoritmo producirá una ruta de vértice$i$ a vértice$j\text{,}$ si existe, y esa ruta será lo más corta posible. Si existe más de un camino de esta longitud, entonces el que se produzca depende del orden en que se examinen los bordes y del orden en que$D_r$ se examinen los elementos de en el Paso 4.
La condición$D_{r }\neq \emptyset$ es análoga a la condición de que no se envíe ningún correo en una etapa determinada del proceso, en cuyo caso MSU no puede conectarse a ESU.
Este algoritmo se puede revisar fácilmente para encontrar rutas a todos los vértices a los que se pueda llegar desde el vértice El$i\text{.}$ paso 5 se popondría hasta que se necesite una ruta específica a un vértice ya que la información en$V$ contiene una lista eficiente de todas las rutas. El algoritmo también se puede ampliar aún más para encontrar caminos entre dos vértices cualesquiera.

Ejemplo$\PageIndex{1}$: A Simple Example

Considera la gráfica a continuación. La existencia de un camino desde el vértice 2 hasta el vértice 3 no es difícil de determinar mediante el examen. Después de unos segundos, deberías poder encontrar dos caminos de longitud cuatro. Algoritmo$\PageIndex{2}$ producirá uno de ellos.

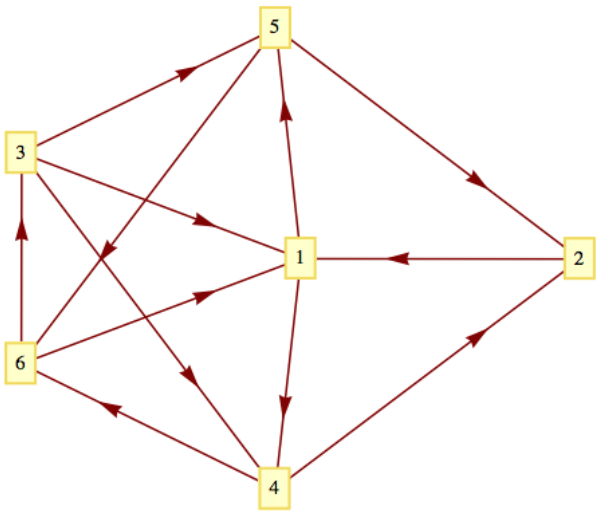$clipboard_e6ad6f21d16a973ac81271b1e5ee9d696.png$ Figura$\PageIndex{1}$: Un ejemplo sencillo de búsqueda en primer plano

Supongamos que los bordes de cada vértice están ordenados en orden ascendente por vértice terminal. Por ejemplo, los bordes del vértice 3 estarían en el orden$(3, 1), (3, 4), (3, 5)\text{.}$ Además, supongamos que en el cuerpo del Paso 4 del algoritmo, los elementos de$D_r$ se utilizan en orden ascendente. Entonces al final del Paso 4, el valor de$V$ será

\ begin {ecuación*}\ begin {array} {cccccccc} k & 1 & 2 & 3 & 4 & 5 & 6 &\\ v_k.\ text {encontrado} & T & T & T & T & T &\ v_k.\ text {from} & 2 & 4 & 6 & 1 & 1 & 4 &\\ text {Profundidad}\ texto {conjunto} & 1 & 1 & 4 &\\ texto {profundidad}\ texto {conjunto} & & 3 & 4 & 2 & 2 & amp; 3 &\\\ end {array}\ end {ecuación*}

Por lo tanto, la ruta$(2, 1, 4, 6, 3)$ es producida por el algoritmo. Tenga en cuenta que si quisiéramos una ruta de 2 a 5, la información en$V$ produce la ruta (2, 1, 5) ya que$V_k.\text{from} = 1$ y$V_1.\text{from} = 2\text{.}$ Un circuito más corto que inicia en el vértice 2 también está disponible al señalar que$V_2.\text{from}=4\text{,}$$V_4\text{.from = 1}\text{,}$ y$V_1.\text{from} = 2\text{;}$ así el circuito$(2, 1, 4, 2)$ es la salida del algoritmo .

Mediciones gráficas

Si tuviéramos que realizar una primera búsqueda de amplitud desde cada vértice en una gráfica, podríamos proceder a determinar varias mediciones clave relacionadas con la conectividad general de esa gráfica. De cada vértice$v\text{,}$ la distancia de$v$ a cualquier otro vértice$w\text{,}$$d(v,w)\text{,}$ es el número de bordes en el camino más corto de$v$ a$w\text{.}$ Este número es también el índice del conjunto de profundidad al que$w$ pertenece en una búsqueda de aliento primero comenzando en$v\text{.}$

\ start {ecuación*} d (v, w) = i\ iff w\ in d_V (i)\ fin {ecuación*}

donde$D_v$ está la familia de conjuntos de profundidad a partir de$v\text{.}$

Si el vector de “valores de” se conoce a partir de la búsqueda de aliento primero, entonces la distancia se puede determinar recursivamente de la siguiente manera:

\ start {ecuación*} d (v, v) =0\ end {ecuación*}

\ begin {ecuación*} d (v, w) = 1 + d (v, w.from)\ textrm {if} w\ neq v\ end {ecuación*}

Ejemplo$\PageIndex{2}$: Computing Distances

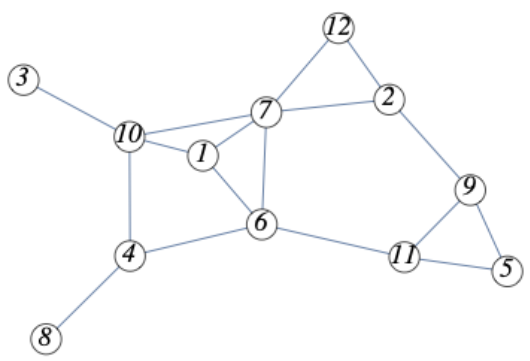$clipboard_e49117af50e44e0dd7578d1caca48da1b.png$ Figura$\PageIndex{2}$: Ejemplo de mediciones de gráficos

Considera Figura$\PageIndex{2}$. Si realizamos una primera búsqueda de amplitud de esta gráfica comenzando en el vértice 2, por ejemplo, obtenemos el siguiente “de datos” diciéndonos a partir de qué vértice se alcanza cada vértice.

\ begin {ecuation*}\ begin {array} {ccccccccccc}\ text {vértice} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 10 & 11 & 12\\ text {vértex.from} & 7 & 2 & 10 & 6 & 9 & 7 & 4 & 2 & 7 & 7 & 9 & 2 & 2\\ end {array}\ end {ecuación*}

Por ejemplo, 4.from tiene un valor de 6. Podemos computar$d(2,4)\text{:}$

\ start {ecuación*}\ begin {split} d (2,4) &= 1+d (2,4.de) = 1+d (2,6)\\ &=2+d (2,6.de) =2+d (2,7)\\ &=3+d (2,7.de) =3+d (2,2)\\ &=3\ end {split}\ end {ecuación*}

Una vez que conocemos las distancias entre dos vértices, podemos determinar la excentricidad de cada vértice; y el diámetro, radio y centro de la gráfica. Primero, definimos estos términos con precisión.

Definición $\PageIndex{1}$: Eccentricity of a Vertex

La distancia máxima de un vértice a todos los demás vértices,$e(v)=max_{w}d(v,w)\text{.}$

Definición $\PageIndex{2}$: Diameter of a Graph

La excentricidad máxima de los vértices en una gráfica, denotada$d(G)\text{.}$

Definición $\PageIndex{3}$: Radius of a Graph

La excentricidad mínima de los vértices en una gráfica, denotada$r(G)\text{.}$

Definición $\PageIndex{4}$: Center of a Graph

El conjunto de vértices con mínima excentricidad,$C(G)=\{v\in V \mid e(v)=r(G)\}$

Ejemplo$\PageIndex{3}$: Measurements from Distance Matrices

Si calculamos todas las distancias entre vértices, podemos resumir los resultados en una matriz de distancias, donde la entrada en fila$i\text{,}$ columna$j$ es la distancia de vértice$i$ a vértice$j\text{.}$ Para la gráfica en Ejemplo$\PageIndex{2}$, esa matriz es

\ begin {ecuation*}\ left (\ begin {array} {cccccccccc} 0 & 2 & 2 & 2 & 3 & 1 & 3 & 3 & 1 & 3 & 1 & 2 & 2 & 2 & 2 & 0 & 3 & 2 & 2 & 1 & 2 & 1 & 2 & 1 & 2 & 1\\ 2 & 3 & 0 & 2 & 5 & 3 & 2 & 3 & 4 & 1 & amp; 4 & 3\\ 2 & 3 & 2 & 0 & 3 & 1 & 2 & 1 & 3 & 1 & 2 & 3 & 3 & 2 & 5 & 3 & 0 & 2 & 3 & 4 & 1 & 4 & 1 & 3 & 3 & 1 & 2 & 2 & 2 & 2 & 1 & 2 & 2 & 1 & 2 & 2 & 1 & 2 & 2 & 2 & 2\ 1 & 2 & 2 & 3 & 1 & 0 & 3 & 2 & 1 & 2 & 1 & 1\ 3 & 4 & 3 & 1 & 4 & 2 & 3 & 0 & 4 & 2 & 3 & 4\ 3 & 1 & 4 & 3 & 1 & 2 & 4 & 0 & 3 & 1 & 2 & 2\ 1 & 2 & 1 & 1 & amp; 2 & 3 & 0 & 3 & 2\\ 2 & 2 & 4 & 2 & 1 & 1 & 2 & 3 & 1 & 3 & 0 & 3\\ 2 & 1 & 3 & 3 & 3 & 2 & 1 & 4 & 2 & 2 & 3 & 0\\ end {array}\ right)\ end {ecuación*}

Si escaneamos la matriz, podemos ver que la distancia máxima es la distancia entre los vértices 3 y 5, que es 5 y es el diámetro de la gráfica. Si nos enfocamos en filas individuales e identificamos los valores máximos, que son las excentricidades, su mínimo es 3, que es el radio de la gráfica. Este valor de excentricidad es alcanzado por vértices en el conjunto$\{1, 4, 6, 7\}\text{,}$ que es el centro de la gráfica.

Nota de Sage Math - Búsqueda de gráficos

La siguiente secuencia de celdas de Sage ilustra cómo se puede hacer la búsqueda en gráficas.

Genera una gráfica aleatoria no dirigida con 18 vértices. Para cada par de vértices, se incluye un borde entre ellos con probabilidad 0.2. Dado que hay bordes$\binom{18}{2}=153$ potenciales, esperamos que haya aproximadamente$0.2 \cdot 153 \approx 31$ bordes. La generación de números aleatorios se siembra primero para que el resultado sea siempre el mismo a pesar de la función de grafo aleatorio. Cambiar o eliminar esa primera línea te permitirá experimentar con diferentes gráficas.

set_random_seed(2002)
Gr=graphs.RandomGNP(18,0.2)
Gr.show()

Contar el número de aristas. En este caso el número es un poco menor de lo esperado.

len(Gr.edges(labels=False))

Encuentra una ruta más corta desde el vértice 0 hasta el vértice 8.

Gr.shortest_path(0, 8)

Generar una lista de vértices que se alcanzarían en una búsqueda en primer plano. La expresión gr.breadth_first_search (0) crea un iterador que es conveniente para la programación. Wrding list () alrededor de la expresión muestra el orden en que se visitan los vértices con el conjunto de profundidad indicado en las segundas coordenadas.

list(Gr.breadth_first_search(0,report_distance='True'))

Ejercicios

Ejercicio$\PageIndex{1}$

Aplicar Algoritmo$\PageIndex{2}$ para encontrar una ruta de 5 a 1 en la Figura$\PageIndex{1}$. Cuál sería el valor final de$V\text{?}$ Supongamos que los vértices terminales en las listas de bordes y elementos de los conjuntos de profundidad se ponen en orden ascendente, como asumimos en Ejemplo$\PageIndex{1}$.

Contestar: $\begin{array}{ccccccc} k & 1 & 2 & 3 & 4 & 5 & 6 \\ V[k].\text{found} & T & T & T & F & F & T \\ V[k].\text{from} & 2 & 5 & 6 & * & * & 5 \\ \text{Depth} \text{Set} & 2 & 1 & 2 & * & * & 1 \\ \end{array}$$\text{(*} = \text{undefined})$

Ejercicio$\PageIndex{2}$

Aplicar Algoritmo$\PageIndex{2}$ para encontrar una ruta de$d$ a$c$ en la gráfica de carreteras en el Ejemplo 9.1.3 usando la lista de bordes en ese ejemplo. Supongamos que los elementos de los conjuntos de profundidad se ponen en orden ascendente.

Ejercicio$\PageIndex{3}$

En una gráfica sencilla no dirigida sin auto-bucles, ¿cuál es el número máximo de aristas que puedes tener, manteniendo la gráfica desconectada? ¿Cuál es el número mínimo de aristas que asegurará que la gráfica esté conectada?

Contestar: Si el número de vértices es puede$n\text{,}$ haber$\frac{(n-1)(n-2)}{2}$ vértices con un vértice no conectado a ninguno de los otros. Un borde más y conectividad está asegurada.

Ejercicio$\PageIndex{4}$

Utilice un algoritmo de difusión para determinar la ruta más corta de vértice$a$ a vértice$i$ en las gráficas que se muestran en la Figura$\PageIndex{3}$ a continuación. Enumere los conjuntos de profundidad y la pila que se crea.

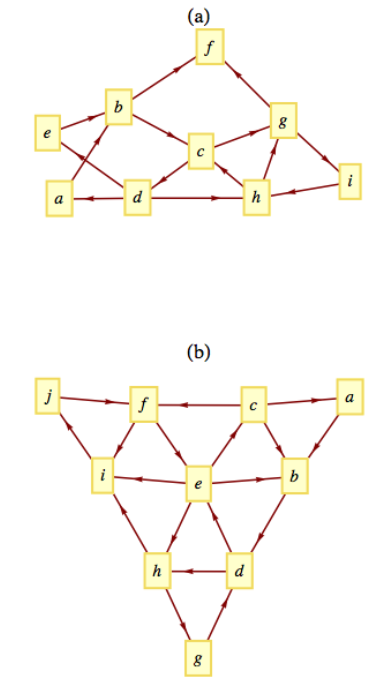$clipboard_e0a6d5b7db98ac15a5d163608b04404af.png$ Figura$\PageIndex{3}$: Trayectorias más cortas de$a$ a$i$?

Ejercicio$\PageIndex{5}$

Para cada una de las siguientes gráficas, determine las excentricidades de cada vértice y el diámetro, radio y centro de la gráfica.

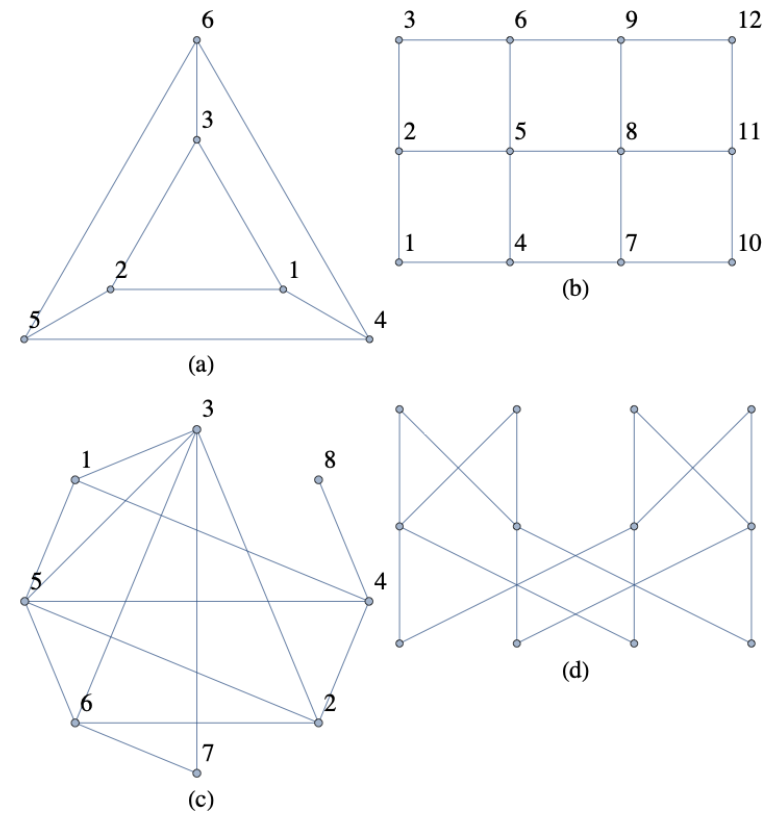$clipboard_ea00d873252400accb94671ab625e86ab.png$ Figura$\PageIndex{4}$: Gráfica no dirigida con 6 vértices.

Contestar

La excentricidad de cada vértice es 2; y el diámetro y el radio son ambos 2 también. Todos los vértices forman parte del centro.
Las esquinas (1,3,10 y 10) tienen excentricidades 5. Los dos vértices centrales, 5 y 8, que están en el centro de la gráfica tienen excentricidad 3. Todos los demás vértices tienen excentricidad 4. El diámetro es de 5. El radio es 3.
Los vértices 1, 2 y 5 tienen excentricidad 2 y conforman el centro de esta gráfica. Los verticies 7 y 8 tienen excentricidad 4, y todos los demás vértices tienen excentricidad 3. El diámetro es de 4. El radio es 2.
La excentricidad de cada vértice es 4; y el diámetro y el radio son ambos 4 también. Todos los vértices forman parte del centro.

Ejercicio$\PageIndex{6}$

Los términos diámetro, radio y centro son familiares en el contexto de los círculos. Compara su uso en círculos y gráficas. ¿Cómo son similares y en qué se diferencian?
La “excentricidad” podría ser menos familiar. ¿Cómo se usa en geometría y tiene un uso compatible en teoría de grafos?

Ejercicio$\PageIndex{7}$

Demostrar (por inducción$k$) que si la relación$r$ en los vértices de una gráfica se define por$v r w$ si hay un borde que se conecta$v$ a$w\text{,}$ entonces$r^k\text{,}$$k \geq 1\text{,}$ se define por$v r^kw$ si hay un camino de longitud$k$ de$v$ a$w\text{.}$

Contestar

Base:$(k=1)$ Es la relación$r^1\text{,}$ definida por$v r^1 w$ si hay una ruta de longitud 1 desde$v \text{ to } w\text{?}$ Sí, ya que$v r w$ si y solo si una arista, que es una ruta de longitud$1\text{,}$ se conecta$v$ a$w\text{.}$

Inducción: Supongamos que$v r^k w$ si y solo si hay un camino$k$ de longitud de$v$ a$w\text{.}$ Debemos mostrar que$v r^{k+1} w$ si y solo si hay un camino de longitud$k+1$ de$v$ a$w\text{.}$

\ begin {ecuación*} v r^ {k+1} w\ Rightarrow v r^k y\ textrm {y} y r w\ textrm {para algún vértice} y\ end {ecuación*}

Por la hipótesis de inducción, hay un camino de longitud$k$ desde$v \textrm{ to } y\text{.}$ Y por la base, hay un camino de longitud uno desde$y$ hasta$w\text{.}$ Si combinamos estos dos caminos, obtenemos un camino de longitud$k+1$ desde$v$ hasta Por$w\text{.}$ supuesto, si comenzamos con un camino de longitud $k+1$de$v$ a$w\text{,}$ tenemos un camino de longitud$k$ de$v$ a algún vértice$y$ y un camino de longitud 1 de$y$ a$w\text{.}$ Por lo tanto,$v r^k y \textrm{ and } y r w \Rightarrow v r^{k+1} w\text{.}$

Ejercicio$\PageIndex{8}$

Para cada una de las siguientes matrices de distancia de gráficas, identifique el diámetro, radio y centro. Supongamos que los vértices de las gráficas son los números 1 a través$n$ de una$n \times n$ matriz.

$\displaystyle \left( \begin{array}{cccccccccc} 0 & 2 & 1 & 2 & 2 & 3 & 3 & 2 & 1 & 1 \\ 2 & 0 & 1 & 2 & 3 & 3 & 3 & 2 & 3 & 2 \\ 1 & 1 & 0 & 1 & 2 & 2 & 2 & 1 & 2 & 1 \\ 2 & 2 & 1 & 0 & 3 & 3 & 3 & 2 & 3 & 2 \\ 2 & 3 & 2 & 3 & 0 & 2 & 1 & 1 & 2 & 1 \\ 3 & 3 & 2 & 3 & 2 & 0 & 1 & 1 & 3 & 2 \\ 3 & 3 & 2 & 3 & 1 & 1 & 0 & 1 & 3 & 2 \\ 2 & 2 & 1 & 2 & 1 & 1 & 1 & 0 & 2 & 1 \\ 1 & 3 & 2 & 3 & 2 & 3 & 3 & 2 & 0 & 1 \\ 1 & 2 & 1 & 2 & 1 & 2 & 2 & 1 & 1 & 0 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cccccccccccc} 0 & 2 & 2 & 2 & 3 & 3 & 3 & 1 & 2 & 3 & 1 & 1 \\ 2 & 0 & 2 & 2 & 1 & 1 & 1 & 3 & 2 & 1 & 1 & 3 \\ 2 & 2 & 0 & 1 & 3 & 2 & 1 & 2 & 2 & 3 & 1 & 1 \\ 2 & 2 & 1 & 0 & 3 & 1 & 2 & 1 & 2 & 3 & 2 & 1 \\ 3 & 1 & 3 & 3 & 0 & 2 & 2 & 4 & 3 & 2 & 2 & 4 \\ 3 & 1 & 2 & 1 & 2 & 0 & 2 & 2 & 3 & 2 & 2 & 2 \\ 3 & 1 & 1 & 2 & 2 & 2 & 0 & 3 & 3 & 2 & 2 & 2 \\ 1 & 3 & 2 & 1 & 4 & 2 & 3 & 0 & 3 & 4 & 2 & 2 \\ 2 & 2 & 2 & 2 & 3 & 3 & 3 & 3 & 0 & 1 & 3 & 1 \\ 3 & 1 & 3 & 3 & 2 & 2 & 2 & 4 & 1 & 0 & 2 & 2 \\ 1 & 1 & 1 & 2 & 2 & 2 & 2 & 2 & 3 & 2 & 0 & 2 \\ 1 & 3 & 1 & 1 & 4 & 2 & 2 & 2 & 1 & 2 & 2 & 0 \\ \end{array} \right)$