9.4: Traversales-Gráficas eulerianas y hamiltonianas
- Page ID
- 117168
El tema de las travesías gráficas tiene una larga historia. De hecho, la solución de Leonhard Euler (Suiza, 1707-83) del Problema del Puente de Koenigsberg es considerada por muchos para representar el nacimiento de la teoría gráfica.
Gráficas eulerianas
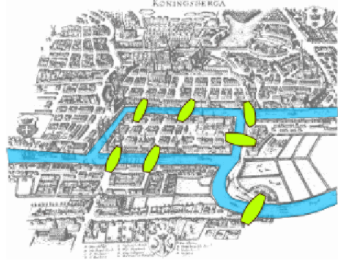 Figura\(\PageIndex{1}\): Un mapa de Koenigsberg, circa 1735
Figura\(\PageIndex{1}\): Un mapa de Koenigsberg, circa 1735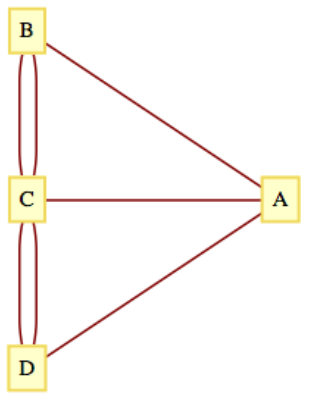 Figura\(\PageIndex{2}\): Multígrafo para los puentes de Koenigsberg
Figura\(\PageIndex{2}\): Multígrafo para los puentes de KoenigsbergUn mapa de la ciudad prusiana de Koenigsberg (circa 1735) en Figura\(\PageIndex{1}\) muestra que había siete puentes que conectaban las cuatro masas de tierra que conformaban la ciudad. La leyenda de este problema afirma que los ciudadanos de Koenigsberg buscaron en vano un recorrido a pie que pasaba por encima de cada puente exactamente una vez. Nadie pudo diseñar tal recorrido y la búsqueda fue abandonada abruptamente con la publicación del Teorema de Euler.
Teorema\(\PageIndex{1}\): Euler's Theorem: Koenigsberg Case
Ningún recorrido a pie por Koenigsberg se puede diseñar para que cada puente se use exactamente una vez.
- Prueba
-
El mapa de Koenigsberg se puede representar como un multígrafo no dirigido, como en la Figura\(\PageIndex{2}\). Las cuatro masas terrestres son los vértices y cada borde representa un puente.
El recorrido deseado es entonces un camino que usa cada borde una vez y solo una vez. Dado que el camino puede comenzar y terminar en dos vértices diferentes, quedan dos vértices que deben ser vértices intermedios en el camino. Si\(x\) es un vértice intermedio, entonces cada vez que visites\(x\text{,}\) debes usar dos de sus bordes incidentes, uno para entrar y otro para salir. Por lo tanto, debe haber un número par de aristas que se conecten\(x\) a los otros vértices. Dado que cada vértice en la gráfica de Koenigsberg tiene un número impar de aristas, no es posible realizar un recorrido del tipo que se desea.
Como es típico de la mayoría de los matemáticos, Euler no estaba satisfecho con resolver solo el problema de Koenigsberg. Su teorema original, que se parafrasea a continuación, se refería a la existencia de caminos y circuitos como los buscados en Koenigsberg. Estos caminos y circuitos se han asociado con el nombre de Euler.
Definición\(\PageIndex{1}\): Eulerian Paths, Circuits, Graphs
Una ruta euleriana a través de una gráfica es una ruta cuya lista de bordes contiene cada borde de la gráfica exactamente una vez. Si el camino es un circuito, entonces se le llama circuito euleriano. Una gráfica euleriana es una gráfica que posee un circuito euleriano.
Ejemplo\(\PageIndex{1}\): An Eulerian Graph
Sin trazar ningún camino, podemos estar seguros de que la gráfica de abajo tiene un circuito euleriano porque todos los vértices tienen un grado par. Esto se desprende del siguiente teorema.
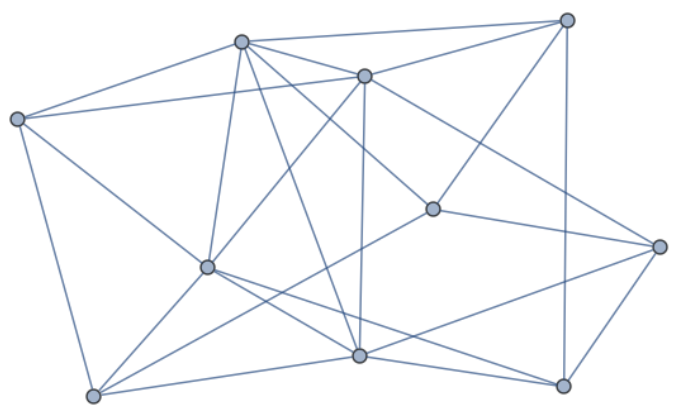 Figura\(\PageIndex{3}\): Una gráfica euleriana
Figura\(\PageIndex{3}\): Una gráfica eulerianaTeorema\(\PageIndex{2}\): Euler's Theorem: General Case
Una gráfica no dirigida tiene una ruta euleriana si y solo si está conectada y tiene cero o dos vértices con un grado impar. Si ningún vértice tiene un grado impar, entonces la gráfica es euleriana.
- Prueba
-
Se puede probar por inducción que el número de vértices en una gráfica no dirigida que tienen un grado impar debe ser par. Dejaremos la prueba de este hecho al lector como ejercicio. La necesidad de tener cero o dos vértices de grado impar se desprende de la prueba del caso Koenigsberg de este teorema. Por lo tanto, nos concentraremos en demostrar que esta condición es suficiente para asegurar que una gráfica tenga un camino euleriano. Dejar\(k\) ser el número de vértices con grado impar.
Fase 1. Si\(k = 0\text{,}\) comienza en cualquier vértice\(v_0\text{,}\) y viaja a lo largo de cualquier camino, sin usar ningún borde dos veces. Dado que cada vértice tiene un grado par, este camino siempre se puede continuar más allá de cada vértice que se alcance excepto\(v_0\text{.}\) El resultado es un circuito que incluye\(v_0\text{.}\) If\(k =2\text{,}\) let\(v_0\) ser cualquiera de los vértices de grado impar. Traza cualquier camino comenzando por\(v_0\) usar bordes ascendentes hasta que no puedas ir más lejos, como en el\(k = 0\) caso. Esta vez, el camino que obtengas debe terminar en el otro vértice de grado impar que\(v_1\text{.}\) llamaremos Al final de la Fase 1, tenemos un camino inicial que puede o no ser euleriano. Si no es euleriana, la Fase 2 puede repetirse hasta que se hayan utilizado todos los bordes. Dado que el número de bordes no utilizados disminuye en cualquier uso de la Fase 2, se debe obtener un camino euleriano en un número finito de pasos.
Fase 2. Al entrar en esta fase, hemos construido un camino que utiliza un subconjunto adecuado de los bordes en nuestra gráfica. Nos referiremos a este camino como el camino actual. \(V\)Dejen ser los vértices de nuestra gráfica,\(E\) los bordes, y\(E_u\) los bordes que se han utilizado en la trayectoria actual. Considera la gráfica\(G' = \left(V, E - E_u\right)\text{.}\) Tenga en cuenta que cada vértice en\(G'\) tiene un grado par. Selecciona cualquier arista,\(e\text{,}\) desde\(G'.\) Let\(v_a\) y\(v_b\) sé los vértices que\(e\) conecta. Trazar una nueva ruta comenzando en\(v_a\) cuyo primer borde es\(e\text{.}\) Podemos estar seguros de que al menos un vértice de la nueva ruta también está en la ruta actual ya que\((V, E)\) está conectado. A partir de\(v_a\text{,}\) ahí existe una ruta\((V, E)\) hacia cualquier vértice en la ruta actual. En algún momento a lo largo de este camino, que podemos considerar el inicio del nuevo camino, habremos intersectado el camino actual. Dado que el grado de cada vértice en\(G'\) es par, cualquier camino en el que iniciemos\(v_a\) puede continuar hasta que sea un circuito. Ahora, simplemente aumentamos la trayectoria de la corriente con este circuito. A medida que viajamos por el camino actual, la primera vez que cruzamos el nuevo camino, viajamos por él (ver Figura\(\PageIndex{4}\)). Una vez que completamos el circuito que es el nuevo camino, retomamos el recorrido de la ruta actual.
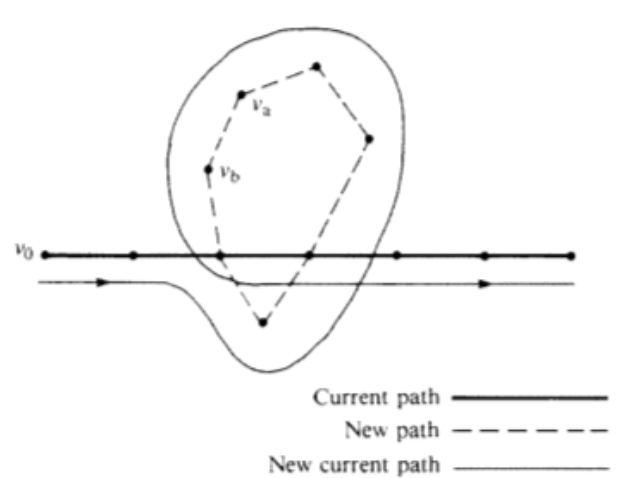 Figura\(\PageIndex{4}\): Plan de aumento de ruta
Figura\(\PageIndex{4}\): Plan de aumento de rutaSi el resultado de esta fase es un camino euleriano, entonces estamos terminados; de lo contrario, repita esta fase.
Ejemplo\(\PageIndex{2}\): Complete Eulerian Graphs
Las gráficas completas no dirigidas\(K_{2n+1}\text{,}\)\(n = 1, 2, 3, \ldots\text{.}\).., son eulerianas. Si\(n \geq 1\text{,}\) entonces no\(K_{2n}\) es euleriano.
Gráficas Hamiltonianas
Buscar un camino que utilice cada vértice de una gráfica exactamente una vez parece ser un siguiente problema natural después de haber considerado los gráficos eulerianos. El matemático irlandés Sir William Rowan Hamilton (1805-65) recibe crédito por definir primero tales caminos. También se le atribuye el descubrimiento de los cuaterniones, por lo que fue honrado por el gobierno irlandés con un sello postal en 2005.
 Figura\(\PageIndex{5}\): Sello irlandés en honor a Sir William Rowan Hamilton
Figura\(\PageIndex{5}\): Sello irlandés en honor a Sir William Rowan HamiltonDefinición\(\PageIndex{2}\): Hamiltonian Path, Circuit, and Graphs
Una ruta hamiltoniana a través de una gráfica es una ruta cuya lista de vértices contiene cada vértice de la gráfica exactamente una vez, excepto si la ruta es un circuito, en cuyo caso el vértice inicial aparece por segunda vez como vértice terminal. Si el camino es un circuito, entonces se le llama circuito hamiltoniano. Una gráfica hamiltoniana es una gráfica que posee un circuito hamiltoniano.
Ejemplo\(\PageIndex{3}\): The Original Hamiltonian Graph
La figura\(\PageIndex{7}\) muestra una gráfica que es hamiltoniana. De hecho, es la gráfica que Hamilton utilizó como ejemplo para plantear la cuestión de la existencia de caminos hamiltonianos en 1859. En su forma original, el rompecabezas que se planteó a los lectores se llamaba “La vuelta al mundo”. Los vértices fueron etiquetados con nombres de las principales ciudades del mundo y el objeto era completar un recorrido por estas ciudades. La gráfica también se conoce como la gráfica de dodecaedro, donde los vértices se corresponden con las esquinas de un dodecaedro y los bordes son los bordes del sólido que conectan las esquinas.
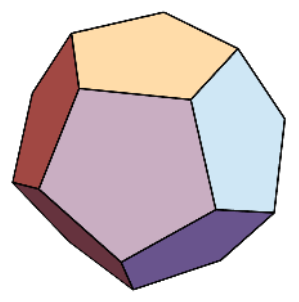 Figura\(\PageIndex{6}\): Un Dodecaedro
Figura\(\PageIndex{6}\): Un Dodecaedro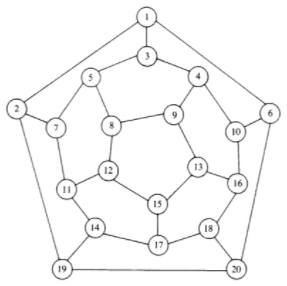 Figura\(\PageIndex{7}\): Gráfica del Dodecaedro
Figura\(\PageIndex{7}\): Gráfica del DodecaedroProblema\(\PageIndex{1}\)
Desafortunadamente, no existe una condición simple que caracterice a una gráfica hamiltoniana. Una condición necesaria obvia es que la gráfica esté conectada; sin embargo, existe una gráfica no dirigida conectada con cuatro vértices que no es hamiltoniana. ¿Se puede dibujar una gráfica así?
Nota\(\PageIndex{1}\): What is Possible and What is Impossible?
La búsqueda de un camino hamiltoniano en una gráfica es típica de muchos problemas de sonido simple en la teoría de grafos que han demostrado ser muy difíciles de resolver. Si bien existen algoritmos simples para realizar la búsqueda, son poco prácticos para problemas grandes porque tardan tanto en completarse a medida que aumenta el tamaño de la gráfica. Actualmente, cada algoritmo para buscar una ruta hamiltoniana en una gráfica lleva un tiempo que crece a una velocidad que es mayor que cualquier polinomio en función del número de vértices. Las tasas de este tipo se denominan “súper polinomios”. Es decir, si\(T(n)\) es el tiempo que lleva buscar una gráfica de\(n\) vértices, y\(p(n)\) es cualquier polinomio, entonces\(T(n) > p(n)\) para todos pero posiblemente un número finito de valores positivos para\(n\text{.}\)
Es una creencia no probada pero ampliamente sostenida de que no existe un algoritmo más rápido para buscar caminos hamiltonianos en las gráficas generales. En resumen, el problema de determinar si una gráfica es hamiltoniana es teóricamente posible; sin embargo, para gráficas grandes la consideramos una imposibilidad práctica. Muchos de los problemas que discutiremos en la siguiente sección, particularmente el Problema del vendedor ambulante, se piensa que son imposibles en el mismo sentido.
Definición \(\PageIndex{3}\): The \(n\)-cube
Dejar\(n \geq 1\text{,}\) y dejar\(B^n\) ser el conjunto de cadenas de 0's y 1's con longitud\(n\text{.}\) El\(n\) -cube es la gráfica no dirigida con un vértice para cada cadena en\(B^n\) y un borde que conecta cada par de cadenas que difieren en exactamente una posición. El\(n\) -cube normalmente se denota\(Q_n\text{.}\)
El\(n\) -cube se encuentra entre las gráficas que se definen dentro del paquete de grafos de SageMath y se crea con la expresión Graphs.Cubegraph (n).
graphs.CubeGraph(4).show(layout="spring")
Ejemplo\(\PageIndex{4}\): Analog-to-Digital Conversion and the Gray Code
Un problema común que se encuentra en la ingeniería es el de la conversión analógico-digital (a-d), donde la lectura en un dial, por ejemplo, debe ser convertida a un valor numérico. Para que esta conversión se realice de manera confiable y rápida, se debe resolver un problema interesante en la teoría de grafos. Antes de que se plantee este problema, haremos la conexión entre la conversión a-d y el problema de la gráfica usando un ejemplo sencillo. Supongamos que un dial puede girarse en cualquier dirección, y que las posiciones se convertirán a uno de los números del cero al siete como se representa en la Figura\(\PageIndex{8}\). Los ángulos de 0 a 360 se dividen en ocho partes iguales, y a cada parte se le asigna un número comenzando por 0 y aumentando en sentido horario. Si los puntos de marcado en alguno de estos sectores la conversión es al número de ese sector. Si el dial está en el límite, entonces estaremos satisfechos con la conversión a cualquiera de los números en los sectores limítrofes. Esta conversión puede pensarse como dando un ángulo aproximado de la esfera, ya que si la esfera está en sector\(k\text{,}\) entonces el ángulo que hace la esfera con el este es aproximadamente\({45k}^{\circ}\text{.}\)
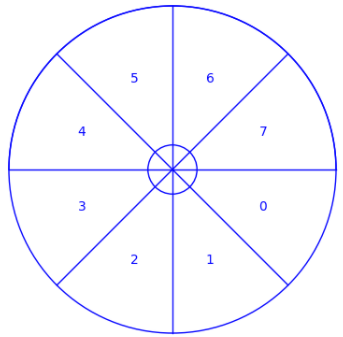 Figura\(\PageIndex{8}\): Dial analógico-digital
Figura\(\PageIndex{8}\): Dial analógico-digitalAhora que se ha identificado la conversión deseada, describiremos una “solución” que tiene un error mayor en ella, para luego identificar cómo se puede rectificar este problema. Todas las computadoras digitales representan números en forma binaria, como una secuencia de 0 y 1 llamada bits, abreviatura de dígitos binarios. Las representaciones binarias de los números 0 a 7 son:
\ begin {ecuación*}\ begin {array} {c} 0= {000} _ {dos} = 0\ cdot 4 + 0\ cdot 2 + 0\ cdot 1\\ 1= {001} _ {dos} = 0\ cdot 4 + 0\ cdot 2 + 1\ cdot 1\ 2= {010} _ {dos} = 0\ cdot 4 + 1\ cdot 2 + 0\ cdot 1\\ 3= {011} _ {dos} = 0\ cdot 4 + 1\ cdot 2 + 1\ cdot 1\\ 4= {100} _ {dos} = 1\ cdot 4 + 0\ cdot 2 + 0\ cdot 1\\ 5= {101} _ {dos} = 1\ cdot 4 + 0\ cdot 2 + 1\ cdot 1\\ 6= {110} _ {dos} = 1\ cdot 4 + 1\ cdot 2 + 0\ cdot 1\\ 7= {111} _ {dos} = 1\ cdot 4 + 1\ cdot 2 + 1\ cdot 1\\ end {array}\ end {ecuación*}
La forma en que podríamos enviar esos bits a una computadora es recubriendo partes de la parte posterior de la esfera con una sustancia metálica, como en la Figura\(\PageIndex{9}\). Para cada uno de los tres círculos concéntricos de la esfera hay un pequeño imán. Si un imán se encuentra debajo de una parte del dial que ha sido recubierta con metal, entonces encenderá un interruptor, mientras que el interruptor permanece APAGADO cuando no se detecta metal por encima de un imán. Observe cómo cada combinación de encendido/apagado de los tres interruptores es posible dada la forma en que se recubre la parte posterior del dial.
Si el dial se coloca de manera que los imanes estén en medio de un sector, esperamos que este método funcione bien. Sin embargo, hay un problema en ciertos límites. Si se gira el dial para que los imanes estén entre los sectores tres y cuatro, por ejemplo, entonces no está claro cuál será el resultado. Esto se debe a que cada imán tendrá solo una fracción del metal requerido por encima de él para encender su interruptor. Debido a las irregularidades esperadas en el recubrimiento del dial, podemos estar seguros al decir que para cada interruptor ya sea ON o OFF podría ser el resultado, y así si el dial está entre los sectores tres y cuatro, se podría indicar cualquier número. Este problema no ocurre entre todos los sectores. Por ejemplo, entre los sectores 0 y 1, solo hay un switch que no se puede predecir. No importa cuál sea el resultado para el interruptor de unidades en este caso, el sector indicado debe ser 0 o 1. Esto congruente con el objetivo original de que un posicionamiento de la esfera en un límite de dos sectores debería producir el número de cualquiera de los sectores.
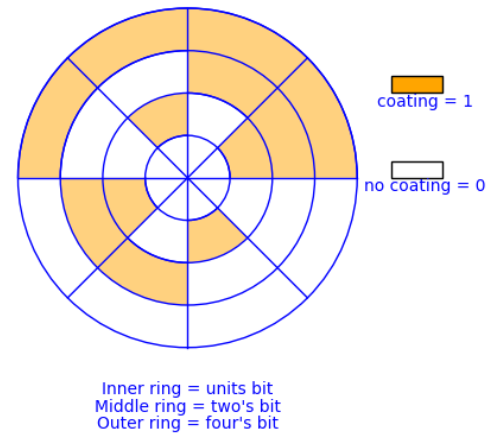 Figura\(\PageIndex{9}\): Esquema de recubrimiento para el dial analógico-digital
Figura\(\PageIndex{9}\): Esquema de recubrimiento para el dial analógico-digital¿Hay alguna manera de recubrir los sectores en la parte posterior del dial para que cada uno de los ocho patrones correspondientes a los números 0 a 7 aparezca una vez, y de manera que entre dos sectores adyacentes cualesquiera haya solo un interruptor que tenga una configuración cuestionable? Lo que aquí estamos describiendo es un circuito hamiltoniano de la (Figura\(\PageIndex{10}\)). Si uno puede dibujar un camino a lo largo de los bordes en el cubo 3 que comienza en cualquier vértice, pasa a través de cada dos vértices una vez, y vuelve al inicio, entonces esa secuencia de patrones de bits se puede usar para recubrir la parte posterior del dial para que entre cada sector solo haya un interruptor cuestionable. Tal camino no es difícil de encontrar, como veremos a continuación.
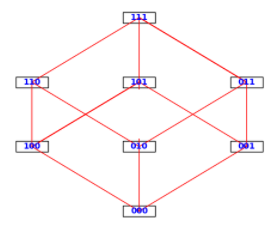 Figura\(\PageIndex{10}\): El 3-Cube
Figura\(\PageIndex{10}\): El 3-CubeMuchos problemas de conversión A-D requieren muchos más sectores y conmutadores que este ejemplo, y pueden ocurrir los mismos tipos de problemas. La solución sería encontrar un camino dentro de una gráfica mucho más grande pero similar. Por ejemplo, podría haber 1,024 sectores con 10 conmutadores, dando como resultado una gráfica con 1,024 vértices. Afortunadamente, nuestra solución se aplicará al\(n\) -cube para cualquier valor positivo de\(n\text{.}\)
Un circuito hamiltoniano del\(n\) -cube se puede describir recursivamente. El circuito en sí, llamado el Código Gris, no es el único circuito hamiltoniano del\(n\) -cubo, sino que es el más fácil de describir. La forma estándar de escribir el Código Gris es como una columna de cadenas, donde la última cadena es seguida por la primera cadena para completar el circuito.
Base para el Código Gris (\(n = 1\)): El Código Gris para el 1-cubo es\(G_1=\left( \begin{array}{c} 0 \\ 1 \\ \end{array} \right)\text{.}\) Tenga en cuenta que el borde entre 0 y 1 se usa dos veces en este circuito. Eso no viola ninguna regla para los circuitos hamiltonianos, pero sólo puede suceder si una gráfica tiene dos vértices.
Definición recursiva del Código Gris: Dado el Código Gris para el\(n\) -cube,\(n \geq 1\text{,}\) entonces\(G_{n+1}\) se obtiene por (1) listado\(G_n\) con cada cadena prefijada con 0, y luego (2) invirtiendo la lista de cadenas en\(G_n\) con cada cadena prefijada con 1. Simbólicamente, la recursión se puede expresar de la siguiente manera, donde\(G_n^r\) está el reverso de la lista\(G_n\text{.}\)
\ begin {ecuación*} G_ {n+1} =\ left (\ begin {array} {c} 0 G_n\\ 1 G_n^r\\\ end {array}\ derecha)\ end {ecuación*}
Los códigos grises para los 2-cube y 3-cube son
\ begin {ecuation*} G_2=\ left (\ begin {array} {c} 00\\ 01\\ 11\\ 10\\ end {array}\ right)\ textrm {y} G_3=\ left (\ begin {array} {c} 000\\ 001\\ 011\ 010\ 110\ 111\\ 101\\ 100\\ end {array}\ derecha)\ final {ecuación*}
Una pregunta podría venir a la mente en este momento. Si los recubrimientos del dial ya no están en la secuencia del 0 al 7, ¿cómo interpretarías los patrones que están en la parte posterior del dial como números del 0 al 7? En el Capítulo 14 veremos que si se usa el Código Gris, esta “decodificación” es bastante fácil.
Ejemplo\(\PageIndex{5}\): Applications of the Gray Code
Una aplicación del código Gray se discutió en la Introducción a este libro. Otra aplicación es en estadística. En un análisis estadístico, a menudo hay una variable que depende de varios factores, pero exactamente qué factores son significativos puede no ser obvio. Para cada subconjunto de factores, habría ciertas cantidades a calcular. Una de esas cantidades es el coeficiente de correlación múltiple para un subconjunto. Si\(A\text{,}\) se conoce el coeficiente de correlación para un subconjunto dado, entonces el valor para cualquier subconjunto que se obtiene ya sea borrando o agregando un elemento a\(A\) ser obtenido rápidamente. Para calcular el coeficiente de correlación para cada conjunto, simplemente viajamos por\(G_n\text{,}\) donde\(n\) está el número de factores que se están estudiando. El primer vértice siempre será la cadena de 0's, que representa el conjunto vacío. Por cada vértice que visites, el conjunto al que corresponde contiene el\(k^{\text{th}}\) factor si el\(k^{\text{th}}\) carácter es un 1.
El 3-cube y su generalización, el\(n\) -cube, juegan un papel en el diseño de un multiprocesador llamado hipercubo. Un multiprocesador es una computadora que consta de varios procesadores independientes que pueden operar simultáneamente y están conectados entre sí por una red de conexiones. En un hipercubo con\(M=2^n\) procesadores, los procesadores están numerados del 0 al\(M-1\text{.}\) Dos procesadores están conectados si sus representaciones binarias difieren exactamente en un bit. El hipercubo ha demostrado ser la mejor red posible para ciertos problemas que requieren el uso de una “supercomputadora”.
Ejercicios
Ejercicio\(\PageIndex{1}\)
Localiza un mapa de la ciudad de Nueva York y dibuja una gráfica que represente sus masas terrestres, puentes y túneles. ¿Hay un camino euleriano por Nueva York? Se puede hacer lo mismo con cualquier otra ciudad que tenga al menos dos masas de tierra.
- Responder
-
Utilizando una hoja de ruta reciente, parece que existe un circuito euleriano en la ciudad de Nueva York, sin incluir las pequeñas islas que pertenecen a la ciudad. Lowell, Massachusetts, se encuentra en la confluencia de los ríos Merrimack y Concord y tiene varios canales que fluyen a través de él. No existe camino euleriano para Lowell.
Ejercicio\(\PageIndex{2}\)
¿Cuál de los dibujos de Figura se\(\PageIndex{11}\) puede dibujar sin quitar el lápiz del papel y sin dibujar ninguna línea dos veces?
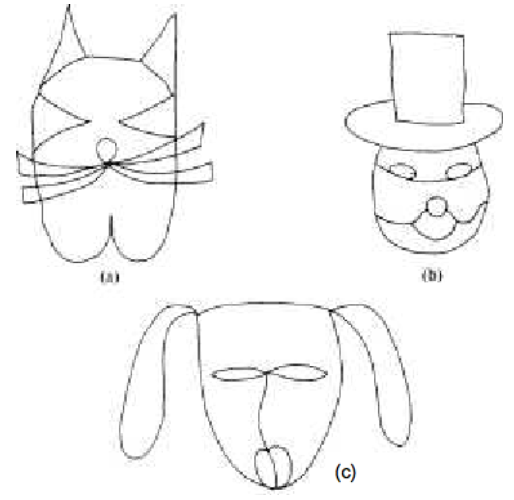 Figura\(\PageIndex{11}\)
Figura\(\PageIndex{11}\)Ejercicio\(\PageIndex{3}\)
Escribe el Código Gris para el 4-cubo.
- Responder
-
Código gris para el cubo 4:
\ begin {ecuation*} G_4=\ left (\ begin {array} {c} 0000\\ 0001\\ 0011\\ 0010\\ 0110\ 0111\\ 0101\\ 0100\\ 1100\\ 1101\ 1111\\ 1110\ 1010\ 1011\ 1001\ 1000\\ end {array}\\ derecha)\ end {ecuación*}
Ejercicio\(\PageIndex{4}\)
Encuentre un circuito hamiltoniano para el gráfico de dodecaedro en la Figura\(\PageIndex{7}\).
Ejercicio\(\PageIndex{5}\)
La Compañía Euler Constructora ha sido contratada para construir un puente adicional en Koenigsberg para que exista un camino euleriano a través del pueblo. Se puede hacer esto, y si es así, ¿dónde se debe construir el puente?
- Responder
-
Cualquier puente entre dos masas de tierra será suficiente. Para conseguir un circuito euleriano, hay que añadir un segundo puente que conecte las dos masas terrestres que no estaban conectadas por el primer puente.
Ejercicio\(\PageIndex{6}\)
Considera las gráficas de la Figura\(\PageIndex{12}\). Determinar cuál de las gráficas tiene un camino euleriano, y encontrar un camino euleriano para las gráficas que tienen uno.
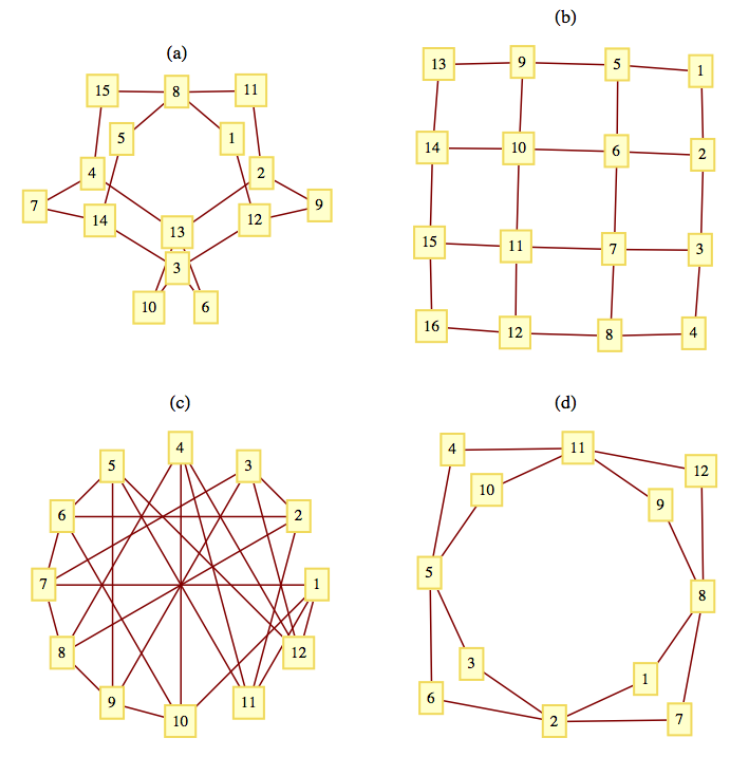 Figura\(\PageIndex{12}\): Gráficas para el ejercicio\(\PageIndex{6}\)
Figura\(\PageIndex{12}\): Gráficas para el ejercicio\(\PageIndex{6}\)Ejercicio\(\PageIndex{7}\)
Formular el teorema de Euler para gráficas dirigidas.
- Responder
-
Dejar\(G=(V,E)\) ser una gráfica dirigida. \(G\)tiene un circuito euleriano si y solo si\(G\) está conectado y\(indeg(v)= outdeg(v)\) para todos\(v \in V\text{.}\) Existe un camino euleriano desde\(v_1 \textrm{ to } v_2\) si y solo si\(G\) está conectado,\(indeg(v_1)=outdeg(v_1)-1\text{,}\)\(indeg(v_2)= outdeg(v_2)+1\text{,}\) y para todos los demás vértices en\(V\) el indegree y outdegree son iguales.
Ejercicio\(\PageIndex{8}\)
Demostrar que el número de vértices en una gráfica no dirigida con grado impar debe ser par.
- Sugerencia
-
Demostrar por inducción en el número de aristas.
Ejercicio\(\PageIndex{9}\)
- ¿En qué condiciones será euleriana una gráfica de torneo round robin?
- Demuestre que cada gráfico de torneo round robin es hamiltoniano.
- Responder
-
Una gráfica de torneo round robin rara vez es euleriana. Será euleriano si tiene un número impar de vértices y cada vértice (equipo) gana exactamente tantas veces como pierda. Cada gráfico de torneo round robin tiene un camino hamiltoniano. Esto se puede probar por inducción en el número de vértices.
Ejercicio\(\PageIndex{10}\)
¿Para qué valores de\(n\) es el\(n\) -cubo euleriano?
Ejercicio\(\PageIndex{11}\)
Un conjunto particular de fichas de dominó tiene 21 fichas:\((1, 1), (1, 2), \dots (1, 6), (2, 2), (2,3), \dots ,(6,6)\text{.}\) ¿Es posible colocar las 21 fichas en una línea para que cada par adyacente de extremos de baldosas coincida (es decir, cada 1 se apoya en un 1, y así sucesivamente)?
- Responder
-
No, tal línea no existe. Las fichas de dominó con dos números diferentes corresponden con bordes en a\(K_6\). Ver dominó y bordes correspondientes en la Figura\(\PageIndex{13}\). Los dominós con dos números iguales podrían retenerse e insertarse en la línea creada con los otros dominós si existe tal línea. Por ejemplo, si\((2,5),\: (5,4)\) fueran parte de la línea,\((5,5)\) podrían insertarse entre esos dos dominós. La línea que queremos existe si y sólo si existe un camino euleriano en un\(K_6\). Dado que los seis vértices de un\(K_6\) grado impar no existe tal trayectoria.
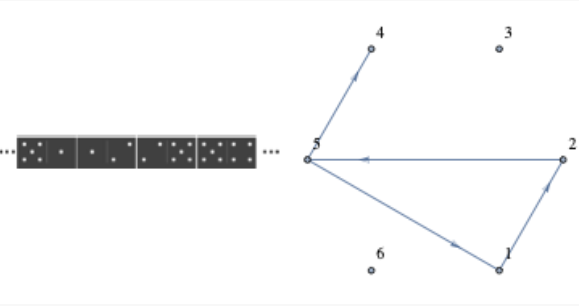
Figura\(\PageIndex{13}\): Correspondencia entre una línea de dominó y un camino en\(K_6\)


