9.5: Optimización de gráficos

Última actualización
Guardar como PDF

Page ID: 117163

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

El hilo conductor que conecta todos los problemas en esta sección es el deseo de optimizar (maximizar o minimizar) una cantidad que se asocia a una gráfica. Concentraremos la mayor parte de nuestra atención en dos de estos problemas, el Problema del Vendedor Viajero y el Problema de Flujo Máximo. Al cierre de esta sección, discutiremos algunos otros problemas comunes de optimización.

Gráficas ponderadas

Definición$\PageIndex{1}$: Weighted Graph

Un gráfico ponderado,$(V, E, w)\text{,}$ es un gráfico$(V, E)$ junto con una función de peso$w: E \to \mathbb{R}\text{.}$ Si$e \in E\text{,}$$w(e)$ es el peso en el borde$e\text{.}$

Como verás en nuestros ejemplos,$w(e)$ suele ser un costo asociado con el borde$e\text{;}$ por lo tanto, la mayoría de los pesos serán positivos.

Ejemplo$\PageIndex{1}$: A Distance Graph

$V$Sea el conjunto de seis capitales en Nueva Inglaterra: Boston, Augusta, Hartford, Providence, Concord y Montpelier. $E$Sea$\{\{a, b\} \in V \times V \mid a\neq b\}\text{;}$ eso es,$(V,E)$ es una gráfica completa desordenada. Un ejemplo de una función de peso en esta gráfica es$w\left(c_1, c _2\right) = \textrm{the distance, in miles, from } c_1 \textrm{ to } c_2\text{.}$

Muchos mapas de carreteras definen funciones de distancia como en la siguiente tabla.

Tabla $\PageIndex{1}$: Distancias entre ciudades capitales en Nueva Inglaterra

—	Augusta	Boston	Concord	Hartford	Montpelier	Providencia
Augusta, ME	—	$165$	$148$	$266$	$190$	$208$
Boston (Massachusetts)	$165$	—	$75$	$103$	$192$	$43$
Concord (Nueva York)	$148$	$75$	—	$142$	$117$	$109$
Hartford (CT)	$266$	$103$	$142$	—	$204$	$70$
Montpelier (Vermont)	$190$	$192$	$117$	$204$	—	$223$
Providence (RI)	$208$	$43$	$109$	$70$	$223$	—

Problema de vendedor ambulante

El Problema del Vendedor Viajero es, dado un gráfico ponderado, encontrar un circuito$\left(e_1, e_2,\ldots ,e_n\right)$ que visite cada vértice al menos una vez y minimice la suma de los pesos,$\sum_{i=1}^n w\left(e_i\right)\text{.}$ Cualquier circuito de este tipo se denomina ruta óptima.

Algunas declaraciones del Problema del Vendedor Viajero requieren que el circuito sea hamiltoniano. En muchas aplicaciones, la gráfica en cuestión estará completa y esta restricción no presenta ningún problema. Si el peso en cada borde es constante, por ejemplo,$w(e) = 1\text{,}$ entonces un camino óptimo sería cualquier circuito hamiltoniano.

Ejemplo$\PageIndex{2}$: The Problem of a Boston Salesman

El problema del vendedor ambulante recibe su nombre de la situación de un vendedor que quiere minimizar el número de millas que recorre al visitar a sus clientes. Por ejemplo, si un vendedor de Boston debe visitar las otras capitales de Nueva Inglaterra, entonces el problema es encontrar un circuito en la gráfica ponderada de Ejemplo$\PageIndex{1}$. Tenga en cuenta que la distancia y el costo están claramente relacionados en este caso. Además, también se podrían tomar en cuenta los peajes y la congestión del tráfico.

La búsqueda de un algoritmo eficiente que resuelva al Vendedor Viajero ha ocupado a los investigadores desde hace años. Si la gráfica en cuestión está completa, existen$(n -1)!$ diferentes circuitos. A medida que$n$ se hace grande, es imposible verificar todos los circuitos posibles. Los algoritmos más eficientes para resolver el problema del vendedor ambulante toman una cantidad de tiempo que es proporcional a$n 2^n\text{.}$ Dado que esta cantidad crece tan rápido, no podemos esperar tener tiempo para resolver el problema del vendedor ambulante para grandes valores de$n\text{.}$ La mayoría de los algoritmos útiles que tienen se han desarrollado tienen que ser heurísticos; es decir, encuentran un circuito que debe estar cerca del óptimo. Uno de esos algoritmos es el algoritmo de “vecino más cercano”, uno de los primeros intentos de resolver el problema del vendedor ambulante. La idea general detrás de este algoritmo es, a partir de cualquier vértice, visitar al vecino más cercano al punto de partida. En cada vértice, el siguiente vértice que se visita es el más cercano al que no se ha alcanzado. Este enfoque miope tipifica algoritmos heurísticos llamados algoritmos codiciosos, que intentan resolver un problema de minimización (maximización) minimizando (maximizando) la cantidad asociada con solo el primer paso.

Algorithm$\PageIndex{1}$: The Closest Neighbor Algorithm

$G = (V, E, w)$Sea un gráfico ponderado completo con$|V| = n\text{.}$ El circuito vecino más cercano a través de G comenzando en$v_1$ se$\left(v_1, v_2,\ldots ,v_n\right)\text{,}$ define por los pasos:

$V_1= V-\left\{v_1\right\}\text{.}$
Para$k\text{ }= 2 \textrm{ to } n - 1$
1. $v_k= \textrm{ the closest vertex in } V_{k-1} \textrm{ to } v_{k-1}\text{:}$
  \ begin {ecuación*} w\ left (v_ {k-1}, v _k\ right) =\ min\ left (w\ left (v_ {k-1}, v\ right)\ mid v\ in V_ {k-1}\ right)\ end {equation*}
  En caso de empate para el más cercano,$v_k$ podrá elegirse arbitrariamente.
2. $\displaystyle V_k= V_{k-1} - \left\{v_k \right\}$
$\displaystyle v_n= \textrm{the only element of } V_n$

El costo del circuito vecino más cercano es$\sum_{k=1}^{n-1} w\left(v_k,v_{k+1}\right)+w\left(v_n,v_1\right)$

Ejemplo$\PageIndex{3}$: A Small Example

El circuito vecino más cercano que comienza en A en la Figura$\PageIndex{1}$ tiene$(1,3,2,4,1)\text{,}$ un costo de 29. El camino óptimo es$(1,2,3,4,1)\text{,}$ con un costo de 27.

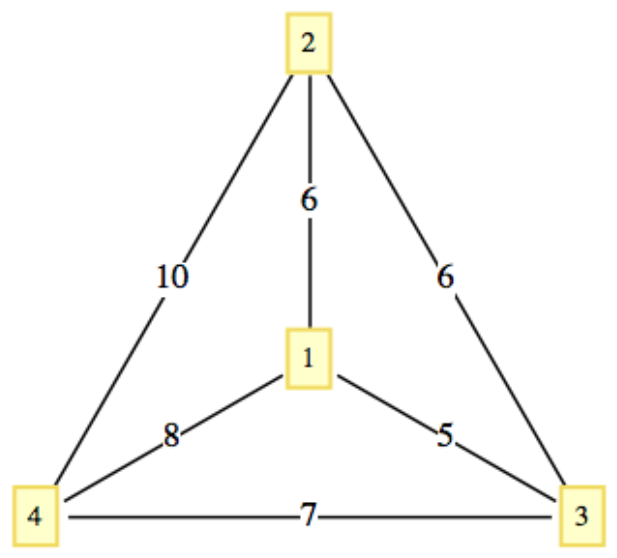$clipboard_e54bb1930d16e5b734db648dbadc38639.png$ Figura$\PageIndex{1}$: Un pequeño ejemplo

Aunque el circuito vecino más cercano a menudo no es óptimo, podemos estar satisfechos si está cerca de lo óptimo. Si$C_{opt}$ y$C_{cn}$ son los costos de los circuitos vecinos óptimos y más cercanos en una gráfica, entonces siempre es el caso de que$C_{opt}\leq C_{cn}$ o$\frac{C_{cn}}{C_{opt}}\geq 1\text{.}$ Podemos evaluar qué tan bueno es el algoritmo de vecino más cercano determinando qué tan pequeña$\frac{C_{cn}}{C_{opt}}$ se vuelve la cantidad. Si siempre está cerca de 1, entonces el algoritmo es bueno. Sin embargo, si hay gráficas para las que es grande, entonces el algoritmo puede ser descartado. Tenga en cuenta que en Ejemplo$\PageIndex{3}$,$\frac{C_{cn}}{C_{opt}} = \frac{29}{27}\approx 1.074\text{.}$ Un aumento del 7 por ciento en el costo puede o no considerarse significativo, dependiendo de la situación.

Ejemplo$\PageIndex{4}$: The One-Way Street

Un vendedor debe hacer paradas en los vértices A, B y C, que están todos en la misma calle de un solo sentido. El gráfico de la Figura$\PageIndex{2}$ está ponderado por la función$w(i, j)$ igual al tiempo que lleva conducir de vértice$i$ a vértice$j\text{.}$

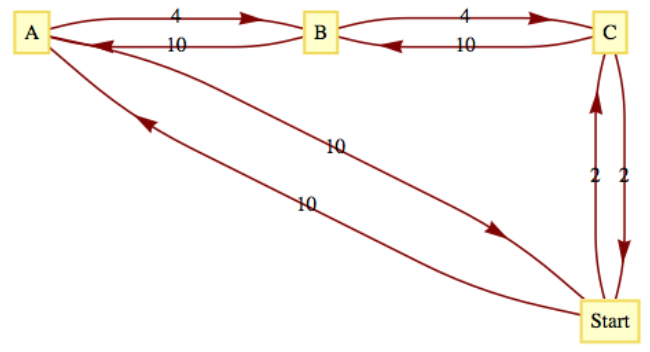$clipboard_e7cebab9a347748b9824ffb13be59380d.png$ Figura$\PageIndex{2}$: Viajar por una calle de un solo sentido

Tenga en cuenta que si$j$ está por la calle unidireccional a partir de$i\text{,}$ entonces$w(i, j) < w(j, i)\text{.}$ Los valores de$C_{opt}\text{,}$ y$C_{cn}$ son 20 y 32, respectivamente. Verifique que$C_{cn}$ sea 32 usando el algoritmo de vecino más cercano. El valor de$\frac{C_{cn}}{C_{opt}} = 1.6$ es significativo en este caso ya que nuestro vendedor pasaría 60 por ciento más de tiempo en la carretera si usara el algoritmo de vecino más cercano.

Un resultado más general relacionado con el algoritmo vecino más cercano presume que la gráfica en cuestión está completa y que la función de peso satisface las condiciones

$w(x, y) = w(y, x)$para todos$x\text{,}$$y$ en el conjunto de vértices, y
$w(x, y) + w(y, z) \geq w(x, z)$para todos$x\text{,}$$y\text{,}$$z$ en el conjunto de vértices.

La primera condición se llama condición de simetría y la segunda es la desigualdad triangular.

Teorema$\PageIndex{1}$

Si$(V, E, w)$ es un gráfico ponderado completo que satisface las condiciones de simetría y desigualdad triangular, entonces

\ begin {ecuación*}\ frac {C_ {cn}} {C_ {opt}}\ leq\ frac {\ lceil\ log_2 (2n)\ rceil} {2}\ end {ecuación*}

Observación$\PageIndex{1}$

Si$|V|=8\text{,}$ entonces este teorema dice que no$C_{cn}$ puede ser mayor que el doble del tamaño de$C_{opt}\text{;}$ sin embargo, no dice que el circuito vecino más cercano necesariamente estará tan lejos de ser un circuito óptimo. A la cantidad$\frac{\left\lceil \log _2 (2n)\right\rceil }{2}$ se le llama un límite superior para la relación$\frac{C_{cn}}{C_{opt}}\text{.}$ Nos dice solamente que las cosas no pueden ser peores que el límite superior. Ciertamente, hay muchas gráficas con ocho vértices de tal manera que los circuitos vecinos óptimos y más cercanos son los mismos. Lo que queda sin afirmar en este teorema es si hay gráficas para las que las cantidades son iguales. Si hay tales gráficas, decimos que el límite superior es agudo.

El valor de$\frac{C_{cn}}{C_{opt}}$ en Ejemplo Ejemplo$\PageIndex{4}$ es 1.6, que es mayor que$\frac{\lceil \log _2 (2\cdot 4)\rceil}{2} = 1.5\text{;}$ sin embargo, la función de peso en este ejemplo no satisface las condiciones del teorema.

Ejemplo$\PageIndex{5}$: The Unit Square Problem

Supongamos que un robot está programado para soldar juntas en placas metálicas cuadradas. Cada placa debe ser soldada en los puntos prescritos en el cuadrado. Para minimizar el tiempo que lleva completar el trabajo, se debe minimizar la distancia total que mueve el brazo de un robot. Dejar$d(P, Q)$ ser la distancia entre$P$ y$Q\text{.}$ Supongamos que antes de que cada placa pueda soldarse, el brazo debe colocarse en un punto determinado$P_0$. Ante una lista de$n$ puntos, queremos ponerlos en orden para que

\ start {ecuación*} d\ izquierda (P _0, P_1\ derecha) + d\ izquierda (P_1, P _2\ derecha) +\ cdots +d\ izquierda (P_ {n-1}, P_n\ derecha) + d\ izquierda (P_n, P _0\ derecha)\ end {ecuación*}

es lo más pequeño posible.

El tipo de problema que se esboza en el ejemplo anterior es de tal importancia que es una de las versiones más estudiadas del Problema del Vendedor Viajero. Lo que sigue es la declaración habitual del problema. Deje$[0, 1] = \{x \in \mathbb{R} \mid \text{ }0 \leq x\leq 1\}\text{,}$ y deje que$S = [0,1]^2\text{,}$ la unidad se cuadre. $n$Dados pares de números reales$\left(x_1, y_1\right),\left(x_2,y_2\right), \dots , \left(x_n,y_n\right)$ en$S$ que representan$n$ los vértices de un$K_n\text{,}$ hallazgo un circuito de la gráfica que minimiza la suma de las distancias recorridas al atravesar el circuito.

Dado que el problema requiere un circuito, no importa en qué vértice comencemos; supongamos que comenzaremos en$\left(x_1,y_1\right)\text{.}$ Una vez que se solucione el problema, siempre podemos cambiar nuestra posición inicial. Una función puede describir de manera más eficiente un circuito en este problema. Cada bijección$f: \{1, . . . , n\} \to \{1, . . . , n\}$ con$f(1) = 1$ describe un circuito

\ begin {ecuación*}\ izquierda (x_1, y_1\ derecha),\ izquierda (x_ {f (2)}, y_ {f (2)}\ derecha),\ ldots,\ izquierda (x_ {f (n)}, y_ {f (n)}\ derecha)\ end {ecuación*}

Hay$(n - 1)!$ tales bijecciones. Dado que un circuito y su inversión tienen el mismo costo asociado, hay$\frac{(n - 1)!}{2}$ casos a considerar. Un examen de todos los casos posibles no es factible para grandes valores de$n\text{.}$

Un algoritmo heurístico popular es el algoritmo de tira:

Algoritmo heurístico$\PageIndex{2}$: The Strip Algorithm

Dados$n$ puntos en el cuadrado unitario:

Fase 1:

Divida el cuadrado en tiras$\left\lceil \sqrt{n/2}\right\rceil$ verticales, como en la Figura$\PageIndex{3}$. Deja que d sea el ancho de cada tira. Si un punto se encuentra en un límite entre dos franjas, considérelo como parte de la franja izquierda.
Partiendo de la izquierda, encuentra la primera tira que contiene uno de los puntos. Localice el punto de partida seleccionando el primer punto que se encuentre en esa franja a medida que viaja de abajo hacia arriba. Supondremos que el primer punto es$\left(x_1,y_1\right)$
Alterna viajando arriba y abajo de las franjas que contienen vértices hasta que se hayan alcanzado todos los vértices.
Regreso al punto de partida.

Fase 2:

Desplace todas las$d/2$ unidades de tiras hacia la derecha (creando una pequeña tira a la izquierda).
Repita los Pasos 1.2 a 1.4 de la Fase 1 con las nuevas tiras.

Cuando las dos fases estén completas, elija el más corto de los dos circuitos obtenidos.

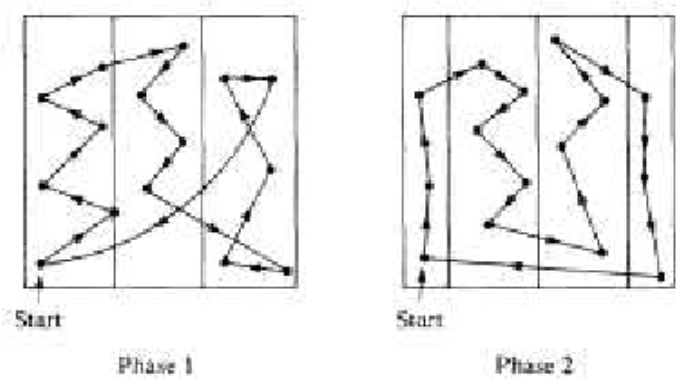$clipboard_e9345b81bdea24713202a068af1b98a77.png$ Figura$\PageIndex{3}$: El algoritmo de la tira

El elemento del paso 3 puede necesitar un poco más de explicación. ¿Cómo viajas arriba o abajo de una franja? En la mayoría de los casos, los vértices en una franja se distribuirán verticalmente de manera que el orden en el que son visitados sea obvio. En algunos casos, sin embargo, el orden podría no estar claro, como en la tercera tira en la Fase I de la Figura$\PageIndex{3}$. Dentro de una tira, el orden en que visitas los puntos (si vas subiendo por la franja) se determina así:$\left(x_i,y_i\right)$ precede$\left(x_j,y_j\right)$ si$y_i <y_j$ o si$y_i=y_j$ y$x_i < x_j$. Al viajar por una tira, reemplace$y_i < y_j$ con$y_i >y_j\text{.}$

La selección de$\left\lceil \sqrt{n/2}\right\rceil$ tiras se realizó en un papel de 1959 de Beardwood, Halton y Hammersley. Equilibra los problemas que surgen si el número de tiras es demasiado pequeño o demasiado grande. Si el cuadrado se divide en muy pocas tiras, algunas tiras pueden estar empaquetadas con vértices para que visitarlas requeriría un movimiento horizontal excesivo. Si se usan demasiadas tiras, el resultado tiende a ser el movimiento vertical excesivo. Una actualización de lo que se sabe sobre este algoritmo está contenida en [39].

Dado que la construcción de un circuito en la plaza consiste en ordenar los puntos dados, no debería sorprender que el algoritmo de tira requiera un tiempo que sea aproximadamente un múltiplo de unidades de$n \log n$ tiempo cuando se van a visitar los$n$ puntos.

El peor caso que se ha encontrado con este algoritmo es aquel en el que el circuito obtenido tiene una distancia total de aproximadamente$\sqrt{2n}$ (ver Sopowit et al.).

Redes y el problema de flujo máximo

Definición$\PageIndex{2}$: Network

Una red es una gráfica dirigida ponderada simple que contiene dos vértices distinguidos llamados el origen y el sumidero con las propiedades de que el indegree de la fuente y el outdegree del sumidero son ambos cero, y source está conectado al sumidero. La función de peso en una red es la función de capacidad, que tiene pesos positivos.

Un ejemplo de una situación real que puede ser representada por una red es el sistema de agua de una ciudad. Un embalse sería la fuente, mientras que un punto de distribución en la ciudad a todos los usuarios sería el fregadero. El sistema de bombas y tuberías que transporta el agua desde la fuente hasta el fregadero constituye la red restante. Podemos suponer que el agua que pasa por una tubería en un minuto es controlada por una bomba y la velocidad máxima está determinada por el tamaño de la tubería y la resistencia de la bomba. Esta velocidad máxima de flujo a través de una tubería se llama su capacidad y es la información que contiene la función de peso de una red.

Ejemplo$\PageIndex{6}$: A City Water System

Considera el sistema que se ilustra en la Figura$\PageIndex{4}$. Los números que aparecen junto a cada tubería indican la capacidad de esa tubería en miles de galones por minuto. Este mapa se puede dibujar en forma de red, como en la Figura$\PageIndex{5}$.

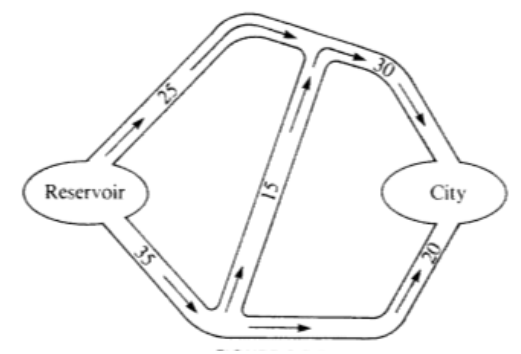$clipboard_e1fb9c72f2ddaa037c67b81e0a3e54530.png$ Figura$\PageIndex{4}$: Sistema de agua de la ciudad

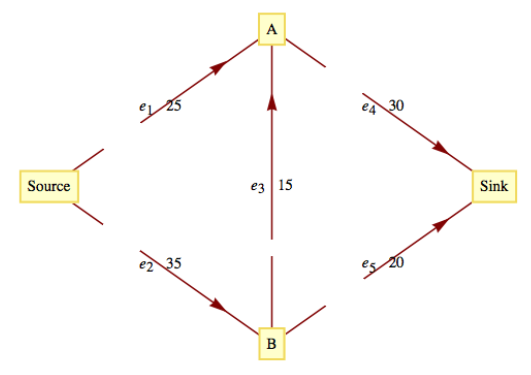$clipboard_e249771da58041a1b152f553fa1cac2ee.png$ Figura$\PageIndex{5}$: Diagrama de flujo para la red de agua de una ciudad

Aunque el material que pasa por esta red es el agua, las redes también pueden representar el flujo de otros materiales, como automóviles, electricidad, bits, llamadas telefónicas o pacientes en un sistema de salud.

Problema$\PageIndex{1}$: The Maximum Flow Problem

El Problema de Flujo Máximo se deriva del objetivo de mover la cantidad máxima de agua u otro material de la fuente al fregadero. Para medir esta cantidad, definimos un flujo como una función$f: E \to \mathbb{R}$ tal que (1) el flujo de material a través de cualquier borde es no negativo y no mayor que su capacidad:$0 \leq f(e) \leq w(e)\text{,}$ para todos$e\in E\text{;}$ y (2) para cada vértice que no sea la fuente y el sumidero, la cantidad total de material que se dirige hacia un vértice es igual a la cantidad total que se dirige:

\ begin {align}\ begin {array} {ccc}\ suma_ {(x, v)\ en E} f (x, v) & = &\ sum_ {(v, y)\ en E} f (v, y)\\ textrm {Flujo hacia} v & = &\ textrm {Flujo de} v\\ end {array}\ label {eq:1}\ end {alinear}

La suma a la izquierda de$\eqref{eq:1}$ representa la suma de los flujos a través de cada borde en$E$ que tiene$v$ como vértice terminal. El lado derecho indica que debe agregar todos los flujos a través de los bordes que inician en$v\text{.}$

Teorema$\PageIndex{2}$: Flow out of Source equals Flow in Sink

Si$f$ es un flujo, entonces$\quad \quad$$\sum_{(\text{source},v)\in E} f(\text{source},v)\text{ }=\sum_{(v,\text{sink})\in E} f(v,\text{sink})$

Prueba

Resta el lado derecho$\eqref{eq:1}$ del lado izquierdo. El resultado es:

\ begin {equation*}\ text {Flow into} v -\ text {Flujo de} v = 0\ end {ecuación*}

Ahora resuma estas diferencias para cada vértice en$V' = V - \{\text{source}, \text{sink}\}\text{.}$ El resultado es

\ comenzar {reunir}\ suma_ {v\ en V'}\ izquierda (\ suma_ {(x, v)\ en E} f (x, v) -\ suma_ {(v, y)\ en E} f (v, y)\ derecha) = 0\ label {eq:2}\ end {reunir}

Ahora observe que si un borde conecta dos vértices en$V'\text{,}$ su flujo aparece como un término tanto positivo como negativo en$\eqref{eq:2}$. Esto quiere decir que los únicos términos positivos que no se cancelan son los flujos hacia el fregadero. Además, los únicos términos negativos que quedan son los flujos que salen de la fuente. Por lo tanto,

\ begin {ecuación*}\ suma_ {(v,\ text {sumidero})\ en E} f (v,\ texto {sumidero}) -\ suma_ {(\ texto {fuente}, v)\ en E} f (\ texto {fuente}, v) =0\ final {ecuación*}

Definición $\PageIndex{3}$: The Value of a Flow

Se demostró que los dos valores fluyen hacia el sumidero y el flujo de salida de la fuente son iguales en Teorema$\PageIndex{2}$ y este valor común se llama el valor del flujo. Se denota por$V(f)\text{.}$ El valor de un flujo representa la cantidad de material que pasa a través de la red con ese flujo.

Dado que el Problema de Flujo Máximo consiste en maximizar la cantidad de material que pasa por una red dada, equivale a encontrar un flujo con el mayor valor posible. Cualquier flujo de este tipo se llama flujo máximo.

Para la red en la Figura$\PageIndex{5}$, un flujo se$f_1\text{,}$ define por$f_1\left(e_1\right)=25\text{,}$$f_1\left(e_2\right)=20\text{,}$$f_1\left(e_3\right)=0\text{,}$$f_1\left(e_4\right)= 25\text{,}$ y$f_1\left(e_5\right)=20\text{.}$ El valor de$f_1\text{,}$$V\left(f_1\right)\text{,}$ es 45. Dado que el flujo total hacia el fregadero no puede ser mayor que 50 ($w \left(e_4\right) + w \left(e_5\right) = 30 + 20$), podemos decir que no$f_1$ está muy lejos de la solución. ¿Se puede mejorar$f_1$ en absoluto? La suma de las capacidades en el fregadero no siempre se puede obtener por un flujo. Lo mismo ocurre con la suma de las capacidades fuera de la fuente. En este caso, la suma de las capacidades fuera de la fuente es de 60, a las que obviamente no se puede llegar en esta red.

Una solución del Problema de Flujo Máximo para esta red es el flujo máximo$f_2\text{,}$ donde$f_2\left(e_1\right)=25\text{,}$$f_2\left(e_2\right)=25\text{,}$$f_2\left(e_3\right)=5\text{,}$$f_2\left(e_4\right)= 30\text{,}$ y$f_2\left(e_5\right)=20\text{,}$ con$V\left(f_2\right) = 50\text{.}$ Esta solución no es única. De hecho, hay un número infinito de flujos máximos para este problema.

Se han desarrollado varios algoritmos para resolver el Problema de Flujo Máximo. Uno de ellos es el Algoritmo de Ford y Fulkerson (FFA). El FFA consiste en encontrar repetidamente rutas en una red llamada rutas de aumento de flujo hasta que no se pueda hacer ninguna mejora en el flujo que se ha obtenido.

Definición$\PageIndex{4}$: Flow Augmenting Path

Dado un flujo$f$ en una red,$(V, E)\text{,}$ una trayectoria de aumento de flujo con respecto a$f$ es una ruta simple desde la fuente hasta el sumidero utilizando bordes tanto en su dirección hacia adelante como en su dirección inversa de tal manera que para cada borde$e$ en la trayectoria,$w(e) - f(e) > 0$ si$e$ se usa en su hacia adelante dirección y$f(e) > 0$ si$e$ se usa en la dirección inversa.

Ejemplo$\PageIndex{7}$: Augmenting City Water Flow

Para$f_1$ en la Figura$\PageIndex{5}$, una trayectoria de aumento de flujo sería$\left(e_2 , e_3 , e_4 \right)$ desde$w\left(e_2\right)-f_1\left(e_2\right)= 15\text{,}$$w\left(e_3\right)-f_1\left(e_3\right)=5\text{,}$ y$w\left(e_4\right)-f_1\left(e_4\right)=5\text{.}$

Estas diferencias positivas representan capacidades no utilizadas, y el valor más pequeño representa la cantidad de flujo que se puede agregar a cada borde en la ruta. Tenga en cuenta que al sumar 5 a cada borde en nuestro camino, obtenemos el$f_2\text{,}$ cual es máximo. Si se usa un borde con un flujo positivo en su dirección inversa, está aportando un movimiento de material que es contraproducente para el objetivo de maximizar el flujo. Es por ello que el algoritmo nos dirige a disminuir el flujo a través de ese borde.

Algorithm$\PageIndex{3}$: The Ford and Fulkerson Algorithm

Definir la función de flujo$f_0$ por$f_0(e)=0$ para cada borde$e \in E\text{.}$
i = 0.
Repetir:
1. Si es posible, encuentre una ruta de aumento de flujo con respecto a$f_i\text{.}$
2. Si existe una ruta de aumento de flujo, entonces:
  1. Determinar
    \ begin {ecuación*}\ begin {split} d & =\ min\ {\ {w (e) - f_i (e)\ mid e\ text {se usa en la dirección hacia delante}\},\\ &\ quad\ quad\ {f_i (e)\ mid e\ text {se usa en la dirección inversa}\}\\\\\ final\ {ecuación*}
  2. Definir$f_{i+1}$ por
    \ begin {ecuación*}\ begin {array} {cc} f_ {i+1} (e) = f_i (e) &\ text {if} e\ text {no es parte de la ruta de aumento de flujo}\\ f_ {i+1} (e) =f_i (e) +d &\ text {if} e\ text {se usa en la dirección hacia adelante}\ f\ _ {i+1} (e) =f_i (e) -d &\ text {si} e\ text {se usa en la dirección inversa}\\\ end {array}\ end {ecuación*}
  3. $\displaystyle i = i + 1$
    hasta que no exista ninguna ruta de aumento de flujo.
Terminar con un flujo máximo$f_i$

Lista$\PageIndex{1}$: Notes on the Ford and Fulkerson Algorithm

Debe quedar claro que cada ruta de aumento de flujo conduce a un flujo de mayor valor y que ninguna de las capacidades de la red puede ser violada.
La búsqueda de profundidad primero debe ser utilizada para encontrar caminos de aumento de flujo, ya que es mucho más eficiente que la búsqueda en amplitud en esta situación. La búsqueda de profundidad primero difiere del algoritmo de amplitud primero en que visitas secuencialmente vértices hasta llegar a un “callejón sin salida” y luego retroceder.
Se han descubierto redes para las cuales el FFA no termina en un número finito de pasos. Todos estos ejemplos tienen capacidades irracionales. Se ha comprobado que si todas las capacidades son números enteros positivos, el FFA termina en un número finito de pasos. Consulta Ford y Fulkerson, Even, o Berge para más detalles.
Cuando usa el FFA para resolver el Problema de Flujo Máximo a mano, es conveniente etiquetar cada borde de la red con la fracción$\frac{f_i(e)}{w(e)}\text{.}$

Algorithm$\PageIndex{4}$: Depth-First Search for a Flow Augmenting Path

Esta es una búsqueda en profundidad para el Hundimiento Iniciando en la Fuente. Let$E'$ ser el conjunto de bordes dirigidos que se pueden utilizar en la producción de una trayectoria de aumento de flujo. Agregar a la red un vértice llamado start y edge$(\text{start}, \text{source}).$

$S = $conjunto de vértices de la red.
$p = $origen$\quad \quad$ Mover$p$ a lo largo del borde$(start, source)$
mientras que no$p$ es igual a iniciar o hundir:
1. si$E'$ existe un borde en que te lleva de$p$ a otro vértice en$S\text{:}$
  \ begin {ecuation*}\ quad\ text {luego establece} p\ text {para que sea ese siguiente vértice y borra el borde de} E'\ end {ecuación*}
  \ begin {ecuación*}\ quad\ text {else reasignar} p\ text {para ser el vértice desde el que se alcanzó} p\ text {(es decir, backtrack)}\ text {.} \ end {ecuación*}
$\text{if } p = \text{start:}$
\ begin {ecuación*}\ text {entonces no existe ninguna ruta de aumento de flujo.} \ end {ecuation*}
\ begin {equation*}\ text {else} p =\ text {sink y has encontrado una ruta de aumento de flujo.} \ end {ecuación*}

Ejemplo$\PageIndex{8}$: A Flow Augmenting Path Going Against the Flow

Considere la red en la Figura$\PageIndex{6}$, donde el flujo de corriente,$f\text{,}$ se indica mediante un etiquetado de los bordes.

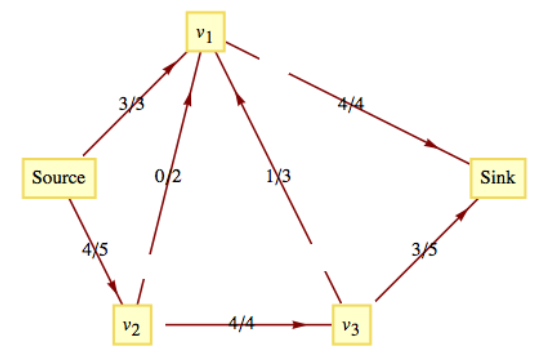$clipboard_ef9cf039ea2ac4f458373acffbfa85e6b.png$ Figura$\PageIndex{6}$: Flujo de corriente

El camino$\left(Source, v_2 , v_1,v_3 , Sink\right)$ es un camino de aumento de flujo que nos permite aumentar el flujo en una unidad. Tenga en cuenta que$\left(v_1,v_3\right)$ se usa en sentido inverso, lo cual está permitido porque$f\left(v_1,v_3\right)>0\text{.}$ El valor del nuevo flujo que obtenemos es 8. Este flujo debe ser máximo ya que las capacidades fuera de la fuente suman 8. Este flujo máximo se define por la Figura$\PageIndex{7}$.

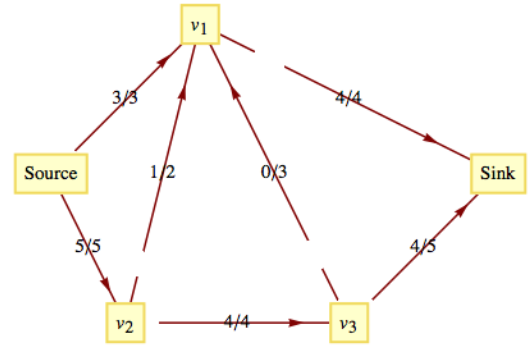$clipboard_e757e8d9afed0f681954f48998bf7b8c3.png$ Figura$\PageIndex{7}$: Flujo actualizado

Otros problemas de optimización de gráficos

El problema del árbol de expansión mínimo: Dado un gráfico ponderado,$(V, E, w)\text{,}$ encuentre un subconjunto$E'$ de$E$ con las propiedades que$(V, E')$ está conectado y la suma de los pesos de los bordes en$E'$ es lo más pequeña posible. Discutiremos este problema en el Capítulo 10.
El problema de coincidencia mínima: Dado un gráfico ponderado no dirigido,$(K, E, w)\text{,}$ con un número par de vértices, empareja los vértices para que cada par esté conectado por un borde y la suma de estos bordes sea lo más pequeña posible. Se ha estudiado extensamente una versión cuadrada unitaria de este problema. Consulte [39] para obtener detalles sobre lo que se sabe de esta versión del problema.
El problema del centro de la gráfica: Dado un gráfico conectado, no dirigido, ponderado, encuentra un vértice (llamado centro) en la gráfica con la propiedad de que la distancia desde el centro a cada otro vértice es lo más pequeña posible. “Lo más pequeño posible” normalmente se interpreta como minimizar la distancia máxima desde el centro hasta un vértice.

Ejercicios

Ejercicio$\PageIndex{1}$

Encuentra el circuito vecino más cercano a través de las seis capitales de Nueva Inglaterra comenzando en Boston. Si comienzas en una ciudad diferente, ¿obtendrás un circuito diferente?

Contestar: El circuito sería Boston, Providence, Hartford, Concord, Montpelier, Augusta, Boston. Sí importa por dónde empieces. Si comienzas en Concord, por ejemplo, tu kilometraje será mayor.

Ejercicio$\PageIndex{2}$

Es la estimación en Teorema$\PageIndex{1}$ aguda para$n = 3\text{?}$ For$n = 4\text{?}$

Ejercicio$\PageIndex{3}$

Dados los siguientes conjuntos de puntos en el cuadrado unitario, encuentra el circuito más corto que visita todos los puntos y encuentra el circuito que se obtiene con el algoritmo de tira.

$\displaystyle \{(0.1k, 0.1k) : k = 0, 1, 2, . . . , 10\}$
$\displaystyle \{(0.1, 0.3), (0.3, 0.8), (0.5, 0.3), (0.7, 0.9), (0.9, 0.1)\}$
$\displaystyle \{(0.0, 0.5), (0.5, 0.0), (0.5, 1.0), (1.0, 0.5)\}$
$\displaystyle \{(0, 0), (0.2, 0.6), (0.4, 0.1), (0.6, 0.8), (0.7, 0.5)\}$

Contestar

Costo óptimo Costo$=2\sqrt{2}\text{.}$ de Fase 1 Costo$=2.4\sqrt{2}\text{.}$ de Fase 2$=2.6\sqrt{2}\text{.}$
Costo óptimo Costo$=2.60.$ de Fase 1 Costo$=3.00\text{.}$ de Fase 2$2\sqrt{2}\text{.}$
$A=(0.0, 0.5), B=(0.5, 0.0), C=(0.5, 1.0), D=(1.0, 0.5)$
Hay 4 puntos; así dividiremos el cuadrado unitario en dos tiras.
- Trayectoria óptima:$(B,A,C,D)\quad \quad \text{Distance } =2\sqrt{2}$
- Trayectoria Fase I:$(B,A,C,D)\quad \quad \text{Distance }=2\sqrt{2}$
- Trayectoria Fase II:$(A,C,B,D) \quad \quad\textrm{Distance }=2+\sqrt{2}$
$A=(0,0), B=(0.2,0.6), C=(0.4,0.1), D=(0.6,0.8), E=(0.7,0.5)$
Hay 5 puntos; así dividiremos el cuadrado unitario en tres tiras.
- Trayectoria óptima:$(A,B,D,E,C)\quad \quad \text{Distance }=2.31$
- Trayectoria Fase I:$(A,C,B,C,E)\quad \quad \text{Distance }= 2.57$
- Trayectoria Fase II:$(A,B,D,E,C) \quad \quad\textrm{Distance }=2.31$

Ejercicio$\PageIndex{4}$

Para$n = 4, 5, \text{and } 6\text{,}$ localizar$n$ puntos en la unidad cuadrada para los que el algoritmo de tira funciona mal.

Ejercicio$\PageIndex{5}$

Considera la red cuyas capacidades máximas se muestran en la siguiente gráfica.

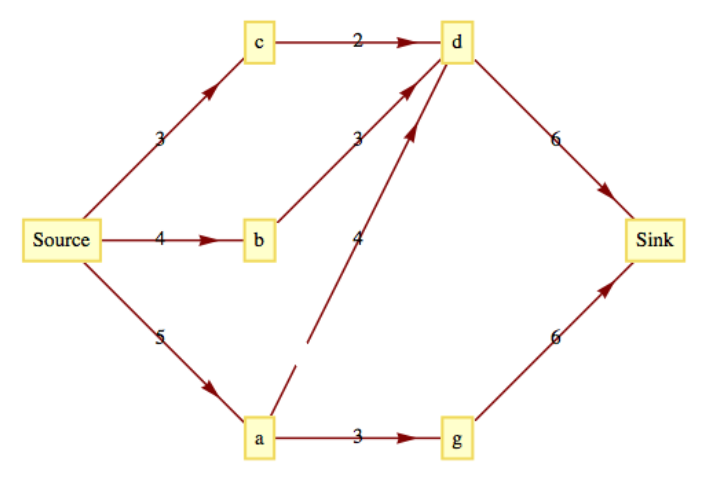$clipboard_ed200eeb56a4356d6dd9e9d3e665887e0.png$ Figura$\PageIndex{8}$

Una función$f$ se define parcialmente en los bordes de esta red por:$f(\text{Source}, c) =2\text{,}$$f(\text{Source}, b) =2\text{,}$$f(\text{Source}, a) = 2\text{,}$ y$f(a, d) = 1\text{.}$ Definir$f$ en el resto de los otros bordes para que$f$ sea un flujo. ¿Cuál es el valor de$f$?
Encuentre una ruta de aumento de flujo con respecto a$f$ para esta red. ¿Cuál es el valor del flujo aumentado?
¿El flujo aumentado es un flujo máximo? Explique.

Contestar

$f(c,d)=2\text{,}$$f(b,d)=2\text{,}$$f(d,k)=5\text{,}$$f(a,g)=1\text{,}$y$f(g,k)=1\text{.}$
Hay tres posibles caminos de aumento de flujo. $s,b,d,k$con incremento de flujo de 1. $s,a,d,k$con incremento de flujo de 1, y$s,a,g,k$ con incremento de flujo de 2.
El nuevo flujo nunca es máximo, ya que siempre existirá otro camino de aumento de flujo. Por ejemplo, si$s,b,d,k$ se usa arriba, el nuevo flujo se puede aumentar en 2 unidades con$s,a,g,k\text{.}$

Ejercicio$\PageIndex{6}$

Dada la siguiente red con función de capacidad$c$ y función de flujo$f\text{,}$ encontrar una función de flujo máximo. Las etiquetas en los bordes de la red son de la forma$f(e)/c(e)\text{,}$ donde$c(e)$ está la capacidad de borde$e$ y$f(e)$ es la capacidad utilizada para el flujo$f\text{.}$

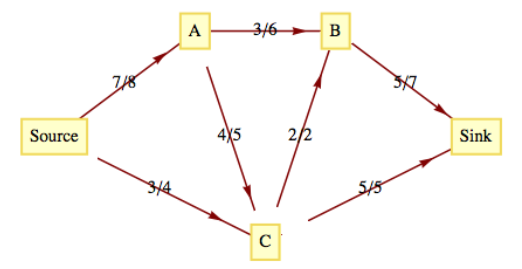$clipboard_e6cc8f5f8109d608f00794105961879fe.png$ Figura$\PageIndex{9}$

Ejercicio$\PageIndex{7}$

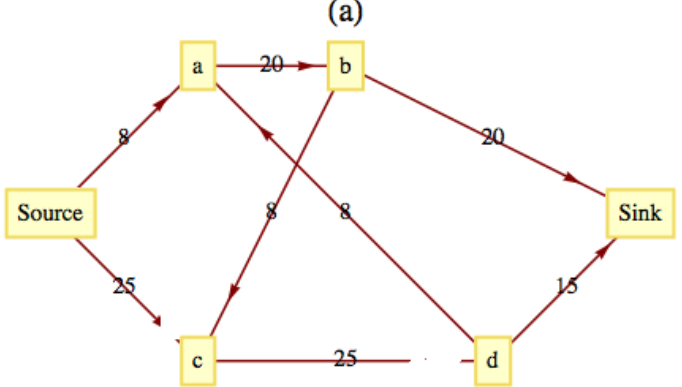$clipboard_e246589752c50ce3aa7fcb183dc039a22.png$ Figura$\PageIndex{10}$

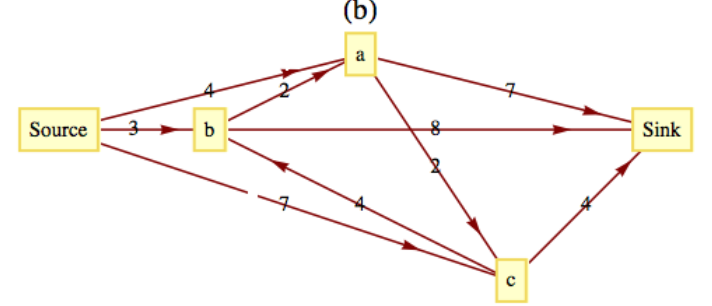$clipboard_e64c8e4c9c6159a5a1fde531587bd262d.png$ Figura$\PageIndex{11}$

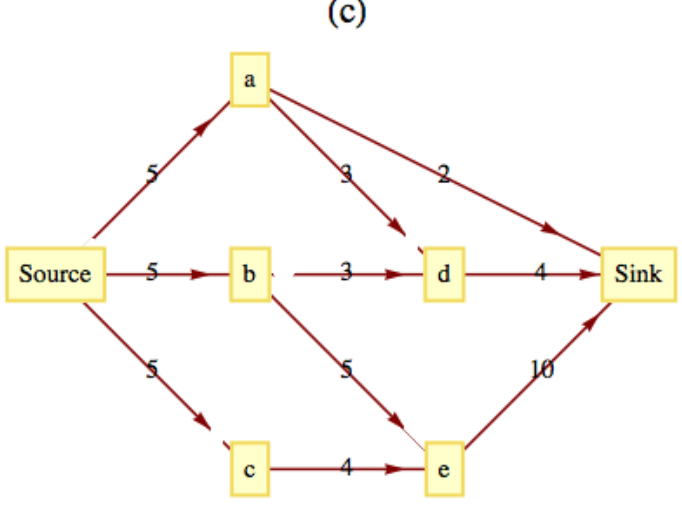$clipboard_e386450f18569fe2083109b21299f3776.png$ Figura$\PageIndex{12}$

Contestar

Valor del flujo máximo$=31\text{.}$
Valor del flujo máximo$=14\text{.}$
Valor del flujo máximo$=14\text{.}$ Consulte la Tabla$\PageIndex{2}$ para una forma de obtener este flujo.

Mesa$\PageIndex{2}$

Paso	Trayectoria de aumento de flujo	Flujo Agregado
1	Fuente,$A$, Fregadero	$2$
2	Fuente,,$C$$B$, Fregadero	$3$
3	Fuente,,$E$$D$, Fregadero	$4$
4	Fuente,,$A$$B$, Fregadero	$1$
5	Fuente,,$C$$D$, Fregadero	$2$
6	Fuente,,$A$,$B$,$C$$D$, Fregadero	$2$

Ejercicio$\PageIndex{8}$

Encuentra dos flujos máximos para la red en la Figura$\PageIndex{6}$ distintos del que se encuentra en el texto.
Describir el conjunto de todos los flujos máximos para la misma red.
Demostrar que si una red tiene dos flujos máximos, entonces tiene un número infinito de flujos máximos.

Ejercicio$\PageIndex{9}$

Discutir las razones por las que el algoritmo de vecino más cercano no se usa en la versión cuadrada de la Unidad del Problema del Vendedor Viajero.

Pista: Contar el número de comparaciones de distancias que se deben hacer.
Contestar: Para ubicar al vecino más cercano entre la lista de$k$ otros puntos en el cuadrado unitario se requiere un tiempo proporcional a$k\text{.}$ Por lo tanto el tiempo requerido para el algoritmo de vecino más cercano con$n$ puntos es proporcional a$(n-1)+(n-2)+\cdots +2+1\text{,}$ lo que es proporcional a$n^2\text{.}$ Dado que la tira algoritmo toma un tiempo proporcional a$n(\log n)\text{,}$ que es mucho más rápido para grandes valores de$n\text{.}$

Ejercicio$\PageIndex{10}$

Explore la posibilidad de resolver el problema del vendedor ambulante en la “caja de unidades”:$[0,1]^3\text{.}$

Ejercicio$\PageIndex{11}$

Idear un algoritmo de “vecino más cercano” para emparejar puntos en el cuadrado unitario.

—	Augusta	Boston	Concord	Hartford	Montpelier	Providencia
Augusta, ME	—	\(165\)	\(148\)	\(266\)	\(190\)	\(208\)
Boston (Massachusetts)	\(165\)	—	\(75\)	\(103\)	\(192\)	\(43\)
Concord (Nueva York)	\(148\)	\(75\)	—	\(142\)	\(117\)	\(109\)
Hartford (CT)	\(266\)	\(103\)	\(142\)	—	\(204\)	\(70\)
Montpelier (Vermont)	\(190\)	\(192\)	\(117\)	\(204\)	—	\(223\)
Providence (RI)	\(208\)	\(43\)	\(109\)	\(70\)	\(223\)	—

Paso	Trayectoria de aumento de flujo	Flujo Agregado
1	Fuente,\(A\), Fregadero	\(2\)
2	Fuente,,\(C\)\(B\), Fregadero	\(3\)
3	Fuente,,\(E\)\(D\), Fregadero	\(4\)
4	Fuente,,\(A\)\(B\), Fregadero	\(1\)
5	Fuente,,\(C\)\(D\), Fregadero	\(2\)
6	Fuente,,\(A\),\(B\),\(C\)\(D\), Fregadero	\(2\)