9.6: Planaridad y Colorantes

Última actualización
Guardar como PDF

Page ID: 117167

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Los temas de esta sección están relacionados con cómo se dibujan las gráficas.

Planaridad: ¿Se puede dibujar una gráfica dada en un plano para que no se intersecten bordes? Ciertamente, es natural evitar las intersecciones, pero hasta ahora no hemos salido de nuestro camino para hacerlo.

Coloraciones: Supongamos que cada vértice en una gráfica no dirigida se va a colorear para que no haya dos vértices que estén conectados por un borde, tengan el mismo color. ¿Cuántos colores se necesitan? Esta pregunta está motivada por el problema de dibujar un mapa para que no haya dos países limítrofes del mismo color. Se puede hacer una pregunta similar para colorear bordes.

Gráficas Planares

Definición$\PageIndex{1}$: Planar Graph/Plane Graph

Un gráfico es plano si se puede dibujar en un plano para que no se crucen bordes. Si se dibuja una gráfica de manera que no se crucen aristas, es una gráfica plana, y dicho dibujo es una incrustación plana de la gráfica.

Ejemplo$\PageIndex{1}$: A Planar Graph

La gráfica en la Figura$\PageIndex{1}$ (a) es plana pero no una gráfica plana. La misma gráfica se dibuja como una gráfica plana en la Figura$\PageIndex{1}$ (b).

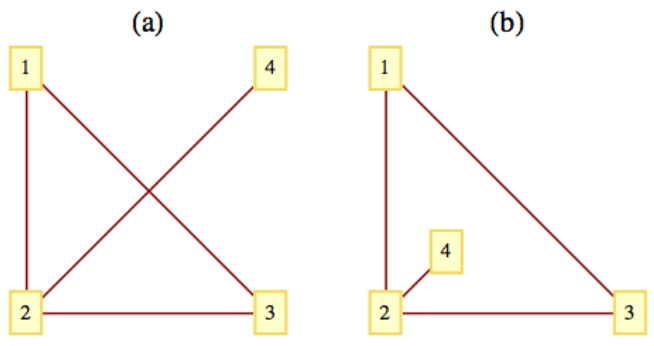$clipboard_e03a1b71fd33a8ff75ca166674e132572.png$ Figura$\PageIndex{1}$: Un gráfico plano

Al discutir la planaridad, solo necesitamos considerar gráficas simples no dirigidas sin auto-bucles. Todas las demás gráficas pueden tratarse como tales ya que todos los bordes que relacionan dos vértices cualesquiera pueden considerarse como un “paquete” que claramente se puede dibujar en un plano.
¿Se te ocurre una gráfica que no sea plana? ¿Cómo probarías que no es planar? Demostrar la inexistencia de algo suele ser más difícil que probar su existencia. Este caso no es la excepción. Intuitivamente, esperaríamos que las gráficas dispersas fueran planas y las gráficas densas serían no planares. El teorema$\PageIndex{2}$ verificará que las gráficas densas son de hecho no planares.
El tema de la planaridad es el resultado de intentar restringir una gráfica a dos dimensiones. ¿Existe un tema análogo para tres dimensiones? ¿Qué gráficas se pueden dibujar en una dimensión?

Definición $\PageIndex{2}$: Path Graph

Un gráfico de ruta de longitud$n\text{,}$ denotado$P_n\text{,}$ es un gráfico no dirigido con$n+1$ vértices$v_0, v_1,\dots, v_n$ que tienen$n$ bordes$\{v_i,v_{i+1}\}\text{,}$$i=0, 1, \dots, n-1\text{.}$

Observación$\PageIndex{1}$: Graphs in Other Dimensions

Si una gráfica solo tiene un número finito de vértices, siempre se puede dibujar en tres dimensiones sin cruces de borde. ¿Esto también es cierto para todas las gráficas con un número infinito de vértices? Las únicas gráficas “unidimensionales” son gráficas que constan de un solo vértice, y gráficas de ruta, como se muestra en la Figura$\PageIndex{2}$.

$clipboard_e32288554b24737f0fd672609f6fab35a.png$ Figura$\PageIndex{2}$: Gráficas unidimensionales

Una discusión sobre la planaridad no está completa sin mencionar el famoso Puzzle de Tres Utilidades. El objeto del rompecabezas es abastecer a tres casas, A, B y C, con los tres servicios públicos, gas, electricidad y agua. La restricción que hace que este rompecabezas sea imposible de resolver es que ninguna línea de utilidad puede cruzarse. No hay incrustación plana de la gráfica en la Figura$\PageIndex{3}$, que comúnmente se denota$K_{3,3}\text{.}$ Esta gráfica es una de las dos gráficas no planares fundamentales. El Teorema de Reducción de Kuratowski establece que si una gráfica no es planar entonces “contiene” ya sea a$K_{3,3}$ o una$K_5\text{.}$ Contención es en el sentido de que si comienzas con una gráfica no planar siempre puedes realizar una secuencia de eliminaciones y contracciones de borde (encogiendo un borde para que los dos vértices conectándolo coincide) para producir una de las dos gráficas.

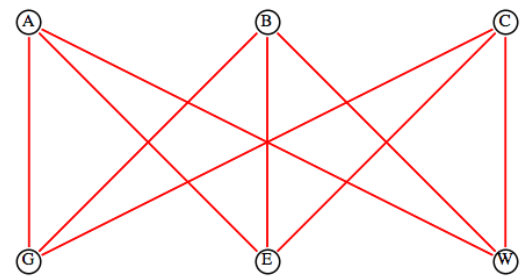$clipboard_ed297e2ec4cce17cae9a271a87f2d537c.png$ Figura$\PageIndex{3}$: El rompecabezas de las tres utilidades

Un gráfico plano divide el plano en una o más regiones. Dos puntos en el plano se encuentran en la misma región si se puede dibujar una curva que conecte los dos puntos que no pasan por una arista. Una de estas regiones será de área infinita. Cada punto del plano es un vértice, un punto en una arista o un punto en una región. Un dato notable sobre la geografía de las gráficas planas es el siguiente teorema que se le atribuye a Euler.

Actividad$\PageIndex{1}$

Experimento: Anote una gráfica en este momento y cuente el número de vértices, regiones y aristas que tenga. Si no$v + r - e$ es 2, entonces tu gráfica es no planar o no está conectada.

Teorema$\PageIndex{1}$: Euler's Formula

Si$G = (V, E)$ es un gráfico plano conectado con$r$ regiones,$v$ vértices y$e$ aristas, entonces

\[\label{eq:1}v+r-e=2\]

Prueba

Demostramos la Fórmula de Euler por Inducción en$e\text{,}$$e \geq 0\text{.}$

Base: Si$e = 0\text{,}$ entonces$G$ debe haber una gráfica con un vértice,$v = 1\text{;}$ y hay una región infinita,$\text{ }r = 1\text{.}$ Por lo tanto,$v + r-e= 1 + 1-0 = 2\text{,}$ y la base es verdadera.

Inducción: Supongamos que$G$ tiene$k$ bordes,$k \geq 1\text{,}$ y que todas las gráficas planas conectadas con menos de$k$ bordes satisfacen$\eqref{eq:1}$. Selecciona cualquier borde que forme parte del límite de la región infinita y llámalo$e_1\text{.}$ Let$G'$ be the graph obtenido de$G$ borrando$e_1\text{.}$ La figura$\PageIndex{4}$ ilustra las dos posibilidades diferentes que necesitamos considerar: o bien$G'$ está conectado o tiene dos conectados componentes,$G_1$ y$G_2\text{.}$

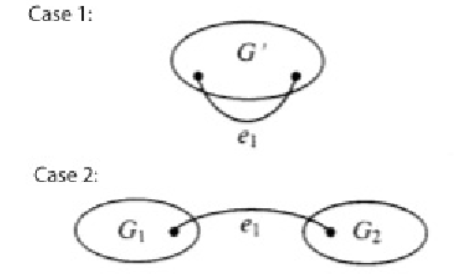$clipboard_eb946f0ae54f97994311d4f05e0ae246e.png$ Figura$\PageIndex{4}$: Dos casos en la prueba de la Fórmula de Euler

Si$G'$ está conectado, se le puede aplicar la hipótesis de inducción. Si$G'$ tiene$v'$ vértices,$r'$ aristas y$e'$ aristas, entonces$v'+r'-e'=2$ y en términos de los números correspondientes para$G\text{,}$

\ begin {ecuation*}\ begin {array} {ll} v'=v &\ textrm {No se eliminaron vértices para formar} G'\\ r'=r-1 &\ textrm {Una región de} G\ textrm {se fusionó con la región infinita cuando} e_1\ textrm {se eliminó}\\ e' = k-1 &\ textrm {asumimos que} G\ textrm {tenía} k\ textrm {bordes.}\\\ end {array}\ fin {ecuación*}

Para el caso donde$G'$ esté conectado,

\ begin {ecuación*}\ begin {split} v+ r -e &= v+r-k\\ &= v' + (r'+1) - (e'+1)\\ & = v' + r'-e'\\ & =2\ end {split}\ end {equation*}

Si no$G'$ está conectado, debe constar de dos componentes conectados,$G_1$ y$G_2\text{,}$ desde que empezamos con una gráfica conectada,$G\text{.}$ podemos aplicar la hipótesis de inducción a cada uno de los dos componentes para completar la prueba. Dejamos a los alumnos que hagan esto, con el recordatorio de que al contar regiones,$G_1$ y$G_2$ compartirán la misma región infinita.

Teorema$\PageIndex{2}$: A Bound on Edges of a Planar Graph

Si$G = (V, E)$ es una gráfica plana conectada con$v$ vértices$v\geq 3\text{,}$ y$e$ aristas, entonces

\[\label{eq:2}e\leq 3v-6\]

Prueba

(Esquema de una Prueba)

Dejar$r$ ser el número de regiones en$G\text{.}$ Para cada región, cuente el número de aristas que componen su borde. La suma de estos recuentos debe ser al menos$3r\text{.}$ Recordemos que aquí estamos trabajando con gráficas simples, por lo que una región hecha por dos aristas que conectan los mismos dos vértices no es posible.
Con base en (a), inferir que el número de aristas$G$ debe ser al menos$\frac{3 r}{2}\text{.}$
$\displaystyle e\geq \frac{3r}{2}\text{ }\Rightarrow \text{ }r\leq \frac{2e}{3}$
Sustituto$\frac{2e}{3}$$r$ en la Fórmula de Euler para obtener una desigualdad equivalente a$\eqref{eq:2}$

Observación$\PageIndex{1}$

Una implicación de$\eqref{eq:2}$ es que el número de aristas en una gráfica plana conectada nunca será mayor que tres veces su número de vértices (siempre y cuando tenga al menos tres vértices). Dado que el número máximo de aristas en una gráfica con$v$ vértices es una función cuadrática de$v\text{,}$ como$v$ aumenta, las gráficas planas son cada vez más escasas.

El siguiente teorema nos será útil a medida que volvamos a la coloración gráfica.

Teorema$\PageIndex{3}$: A Vertex of Degree Five

Si$G$ es una gráfica plana conectada, entonces tiene un vértice con grado 5 o menos.

Prueba: (por contradicción): Podemos suponer que$G$ tiene al menos siete vértices, pues de lo contrario el grado de cualquier vértice es como máximo 5. Supongamos que$G$ es una gráfica plana conectada y cada vértice tiene un grado de 6 o más. Entonces, ya que cada arista contribuye al grado de dos vértices,$e\geq \frac{6v}{2}=3v\text{.}$ Sin embargo, el Teorema$\PageIndex{2}$ afirma que el$e\leq 3v-6 < 3v\text{,}$ que es una contradicción.

Colorear Gráfica

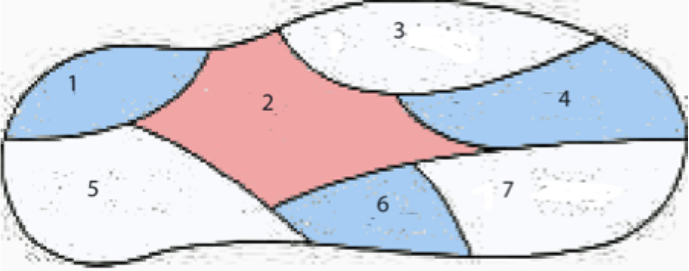$clipboard_e87fc2efd28861812ce1cc9b29e366580.png$ Figura$\PageIndex{5}$: Una coloración 3 de la isla de Euler

El mapa de Isla Euler en Figura$\PageIndex{5}$ muestra que hay siete pueblos en la isla. Supongamos que un cartógrafo debe producir un mapa coloreado en el que no tengan el mismo color dos pueblos que compartan un límite. Para mantener bajos los costos, quiere minimizar la cantidad de colores diferentes que aparecen en el mapa. ¿Cuántos colores son suficientes? Para Euler Island, la respuesta es tres. Aunque podría no ser obvio, se trata de un problema gráfico. Podemos representar el mapa con una gráfica, donde los vértices son países y un borde entre dos vértices indica que los dos países correspondientes comparten un límite de longitud positiva. Este problema motiva un problema más general.

Definición $\PageIndex{3}$: Graph Coloring

Dada una gráfica no dirigida$G = (V, E)\text{,}$ encontramos una “función de coloración”$f$ desde$V$ dentro de un conjunto de colores$H$ tales que$\left(v_i,v_j\right)\in E \Rightarrow f\left(v_i\right)\neq f\left(v_j\right)$ y$H$ tiene la menor cardinalidad posible. La cardinalidad de$H$ se llama el número cromático de$G\text{,}$$\chi(G)\text{.}$

Una función de coloración en un conjunto de$n$ elementos se llama$n$ -coloring.
En términos de este problema general, el número cromático de la gráfica de la isla de Euler es tres. Para ver que no se necesitan más de tres colores, solo necesitamos mostrar un 3-color:$f(1) = f(4) = f(6) = \text{blue}\text{,}$$f(2) = \text{red}\text{,}$ y$f(3) = f(5) = f(7) = \text{white}\text{.}$ Esta coloración no es única. El siguiente conjunto de colores más pequeño sería de dos colores, y deberías poder convencerte de que no existe 2 colores para esta gráfica.

A mediados del siglo XIX, quedó claro que la típica gráfica plana tenía un número cromático de no más de 4. En ese punto, los matemáticos atacaron la Conjetura de Cuatro Colores, que es que si$G$ es alguna gráfica plana, entonces su número cromático no es mayor que 4. Si bien la conjetura es bastante fácil de afirmar, tardó más de 100 años, hasta 1976, en probar la conjetura afirmativa.

Teorema$\PageIndex{4}$: The Four-Color Theorem

Si$G$ es una gráfica plana, entonces$\chi (G)\leq 4\text{.}$

Una prueba del Teorema de los Cuatro Colores está más allá del alcance de este texto, pero podemos probar un teorema que es sólo 25 por ciento inferior.

Teorema$\PageIndex{5}$: The Five-Color Theorem

Si$G$ es una gráfica plana, entonces$\chi (G)\leq 5\text{.}$

Prueba

El número 5 no es un límite superior agudo para$\chi(G)$ debido al Teorema de Cuatro Colores.

Esta es una prueba por Inducción sobre el Número de Vértices en la Gráfica.

Base: Claramente, una gráfica con un vértice tiene un número cromático de 1.

Inducción: Supongamos que todas las gráficas planas con$n - 1$ vértices tienen un número cromático de 5 o menos. Dejar$G$ ser una gráfica plana. Por Teorema$\PageIndex{3}$, existe un vértice$v$ con$\deg v \leq 5\text{.}$ Let$G - v$ be la gráfica plana obtenida al eliminar$v$ y todos los bordes que se conectan$v$ a otros vértices en$G\text{.}$ Por la hipótesis de inducción,$G - v$ tiene un 5-coloración. Supongamos que los colores utilizados son rojo, blanco, azul, verde y amarillo.

Si$\deg v < 5\text{,}$ entonces podemos producir una coloración 5 de$G$ seleccionando un color que no se usa para colorear los vértices a los que están conectados$v$ con un borde en$G\text{.}$

Si$\deg v = 5\text{,}$ entonces podemos usar el mismo enfoque si los cinco vértices que están adyacentes a no$v$ están todos coloreados de manera diferente. Ahora nos queda la posibilidad de que$v_1\text{,}$$v_2\text{,}$$v_3\text{,}$$v_4\text{,}$ y todos$v_5$ estén conectados$v$ por un borde y todos estén coloreados de manera diferente. Supongamos que son de color rojo, blanco azul, amarillo y verde, respectivamente, como en la Figura$\PageIndex{6}$.

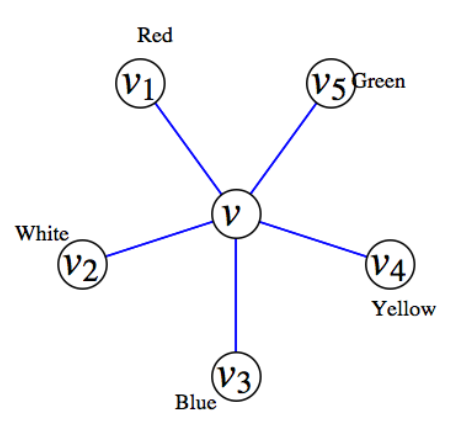$clipboard_e73cc19235803ee449bfbe42b84ff93bf.png$ Figura$\PageIndex{6}$

A partir de$v_1$ en$G-v\text{,}$ supongamos que intentamos construir un camino$v_3$ que pase solo por vértices rojos y azules. Esto se puede lograr o no se puede lograr. Si no se puede hacer, considere todos los caminos que comienzan en$v_1\text{,}$ y atraviesan solo vértices rojos y azules. Si intercambiamos los colores de los vértices en estos caminos, incluyendo todavía$v_1$ tenemos un 5-color de$G - v\text{.}$$v_1$ Since ahora es azul, podemos colorear el vértice central,$v\text{,}$ rojo.

Por último, supongamos que$v_1$ está conectado al$v_3$ uso únicamente de vértices rojos y azules. Luego un camino de$v_{1 }$ a$v_3$ mediante el uso de vértices rojos y azules seguido de los bordes$\left(v_3,v\right)$ y$\left(v,v_1\right)$ completa un circuito que encierra$v_2$ o encierra$v_4$ y$v_5\text{.}$ Por lo tanto, ningún camino de$v_2$ a$v_4$ existe usando solo vértices blancos y amarillos . Entonces podemos repetir el mismo proceso que en el párrafo anterior con$v_2$ y$v_4\text{,}$ que nos permitirá colorear v blanco.

Definición$\PageIndex{4}$: Bipartite Graph

Una gráfica bipartita es una gráfica que tiene una coloración 2. Equivalentemente, una gráfica es bipartita si sus vértices se pueden dividir en dos subconjuntos no vacíos para que ningún borde conecte vértices del mismo subconjunto.

Ejemplo$\PageIndex{2}$: A Few Examples

La gráfica del Puzzle de Tres Utilidades es bipartita. Los vértices están particionados en los servicios públicos y los hogares. Por supuesto un color 2 de la gráfica es para colorear los servicios públicos de rojo y los hogares de azul.
Para$n\geq 1\text{,}$ el$n$ -cube es bipartito. Una coloración sería colorear todas las cadenas con un número par de 1's rojo y las cuerdas con un número impar de 1's azul. Por la definición del$n$ -cube, no se pudieron conectar dos cadenas que tienen el mismo color ya que necesitarían diferir en al menos dos posiciones.
Dejar$V$ ser un conjunto de 64 vértices, uno por cada cuadrado en un tablero de ajedrez. Podemos indexar los elementos de$V$ por$\quad \quad$$v_{i j}$ = el cuadrado en la fila$i\text{,}$ columna$j\text{.}$ Conecta vértices en$V$ según si puedes o no mover a un caballero de un cuadrado a otro. Usando nuestra indexación de$V\text{,}$$\quad \quad$$\left(v_{i j}, v_{k l}\right)\in E\text{ if and only if } \begin{array}{c} |i-k|+|j-l|=3 \\ \text{and } |i-k|\cdot |j-l|=2 \\ \end{array}$$(V, E)$ es una gráfica bipartita. La coloración habitual de un tablero de ajedrez es válida 2-coloración.

¿Cómo se puede reconocer si una gráfica es bipartita? A diferencia de la planaridad, hay una buena condición equivalente para que una gráfica sea bipartita.

Teorema$\PageIndex{6}$: No Odd Circuits in a Bipartite Graph

Una gráfica no dirigida es bipartita si y sólo si no tiene circuito de longitud impar.

Prueba

($\Rightarrow$) Let$G = (V, E)$ Ser una gráfica bipartita que se divide en dos conjuntos, R (ed) y B (lue) que definen una 2-coloración. Considera cualquier circuito en$V\text{.}$ Si especificamos una dirección en el circuito y definimos$f$ en los vértices del circuito por

\ begin {ecuación*} f (u) =\ textrm {el siguiente vértice en el circuito después de} v\ end {ecuación*}

Tenga en cuenta que$f$ es una bijección. De ahí que el número de vértices rojos en el circuito sea igual al número de vértices azules, por lo que la longitud del circuito debe ser pareja.

($\Longleftarrow$) Supongamos que no$G$ tiene circuito de longitud impar. Para cada componente de$G\text{,}$ seleccionar cualquier vértice$w$ y colocarlo rojo. Entonces por cada otro vértice$v$ en el componente, encuentra el camino de la distancia más corta de$w$ a$v\text{.}$ Si la longitud del camino es impar, color$v$ azul, y si es par, color$v$ rojo. Afirmamos que este método define una 2-coloración de$G\text{.}$ Supongamos que no define una 2-coloración. Entonces dejar$v_a$ y$v_b$ ser dos vértices con colores idénticos que están conectados con un borde. Por cierto que$G\text{,}$ no coloreamos$v_a$ ni$v_{b }$$w\text{.}$ podíamos igualar Ahora podemos construir un circuito con una longitud impar en$G\text{.}$ Primero, partimos en$w$ y seguimos el camino más corto para$v_a$. Después siga el borde$\left(v_a,v_b\right)\text{,}$ y finalmente, siga el reverso de un camino más corto de$w$ a$v_b\text{.}$ Since$v_a$ y$v_b$ tengan el mismo color, los segmentos primero y tercero de este circuito tienen longitudes que son a la vez impares o pares, y la suma de sus longitudes debe ser par. La suma del borde único nos$\left(v_a,v_b\right)$ muestra que este circuito tiene una longitud impar. Esto contradice nuestra premisa.

Ejercicios

Ejercicio$\PageIndex{1}$

Aplicar Teorema$\PageIndex{3}$ para demostrar que una vez que$n$ llega a un cierto tamaño, a$K_n$ es no planar. ¿Cuál es la gráfica plana completa más grande?

Contestar: El teorema se$\PageIndex{3}$ puede aplicar para inferir que si$n\geqslant 5\text{,}$ entonces$K_n$ es no planar. A$K_4$ es la gráfica plana completa más grande.

Ejercicio$\PageIndex{2}$

¿Se puede aplicar Teorema$\PageIndex{3}$ para demostrar que el Rompecabezas de las Tres Utilidades no se puede resolver?

Ejercicio$\PageIndex{3}$

¿Cuáles son los números cromáticos de las siguientes gráficas?

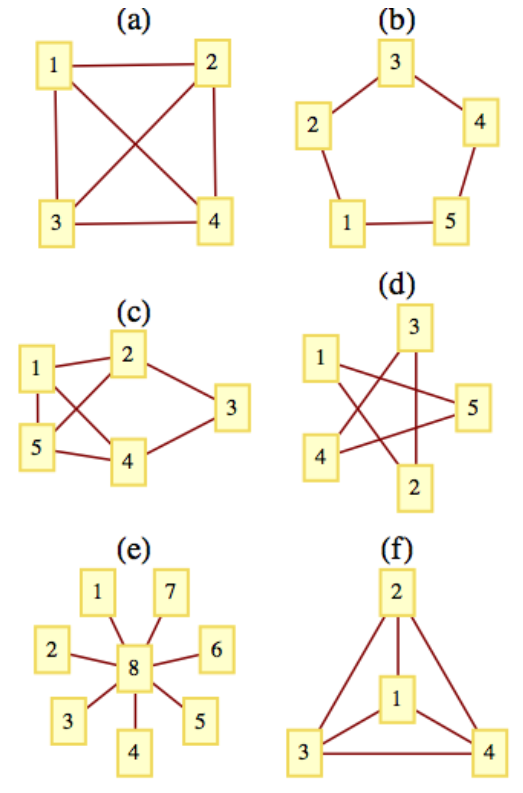$clipboard_e4e6b8e8a2e8135f3dd319f1db96e76a0.png$ Figura$\PageIndex{7}$: ¿Cuáles son los números cromáticos?

Contestar

$4$
$3$
$3$
$3$
$2$
$4$

Ejercicio$\PageIndex{4}$

Demostrar que si una gráfica no dirigida tiene un subgrafo que es un$K_3$ it entonces su número cromático es al menos 3.

Ejercicio$\PageIndex{5}$

Qué es$\chi \left(K_n\right)\text{,}$$n\geq 1\text{?}$

Contestar: El número cromático es$n$ ya que cada vértice está conectado a cada otro vértice.

Ejercicio$\PageIndex{6}$

¿Cuál es el número cromático de Estados Unidos?

Ejercicio$\PageIndex{7}$

Completa la prueba de la Fórmula de Euler, Teorema$\PageIndex{1}$.

Contestar

Supongamos que no$G'$ está conectado. Entonces$G'$ se compone de 2 componentes que son gráficos planos con menos de$k$ aristas,$G_1$ y$G_2\text{.}$ para$i=1,2$ dejar$v_i,r_i, \text{and} e_i$ ser el número de vértices, regiones y aristas en$G_i\text{.}$ Por la hipótesis de inducción,$v_i+r_i-e_i=2$ para$i=1,2\text{.}$

Una de las regiones, la infinita, es común a ambas gráficas. Por lo tanto, cuando agregamos edge de$e$ nuevo a la gráfica, tenemos$r=r_1+r_2-1\text{,}$$v=v_1+v_2\text{,}$ y$e=e_1+e_2+1\text{.}$

\ begin {ecuación*}\ begin {split} v+r-e &=\ left (v_1+v_2\ right) +\ left (r_1+r_2-1\ right) -\ left (e_1+e_2+1\ right)\\ &=\ left (v_1+r_1-e_1\ right) +\ left (v_2+r_2-e_2\ right)\ -2\ &=2 + 2 -2\\ &=2\ end {split}\ end {ecuación*}

Ejercicio$\PageIndex{8}$

Utilice el esquema de una prueba de teorema$\PageIndex{2}$ para escribir una prueba completa. No dejes de señalar dónde$v\geq 3$ es esencial la premisa.

Ejercicio$\PageIndex{9}$

Dejar$G = (V,E)$ con$|V|\geq 11\text{,}$ y dejar$U$ ser el conjunto de todos los bordes no dirigidos entre distintos vértices en$V\text{.}$ Probar que cualquiera$G$ o$G' = \left(V,E^c\right)$ es no planar.

Contestar: Ya que$\left| E\right| +E^c=\frac{n(n-1)}{2}\text{,}$ cualquiera$E \text{ or } E^c$ tiene al menos$\frac{n(n-1)}{4}$ elementos. Supongamos que es$E$ que es más grande. Ya que$\frac{n(n-1)}{4}$ es mayor de$3n-6\text{ }\text{for}\text{ }n\geqslant 11\text{,}$$G$ lo que sería no planar. Por supuesto, si$E^c$ es más grande, entonces$G'$ sería no planar por el mismo razonamiento. ¿Se puede encontrar una gráfica con diez vértices tal que sea plana y su complemento también sea planar?

Ejercicio$\PageIndex{10}$

Diseñar un algoritmo para determinar si una gráfica es bipartita.

Ejercicio$\PageIndex{11}$

Demostrar que una gráfica bipartita con un número impar de vértices mayor o igual a 3 no tiene circuito hamiltoniano.

Contestar: Supongamos que$(V,E)$ es bipartito (con colores rojo y azul),$\left| E\right|$ es impar, y$\left(v_1,v_2,\ldots ,v_{2n+1},v_1\right)$ es un circuito hamiltoniano. Si$v_1$ es rojo, entonces también$v_{2n+1}$ sería rojo. Pero entonces no$\left\{v_{2n+1},v_1\right\}$ estaría en$E\text{,}$ contradicción.

Ejercicio$\PageIndex{12}$

Demostrar que cualquier gráfica con un número finito de vértices se puede dibujar en tres dimensiones para que no se crucen aristas.

Ejercicio$\PageIndex{13}$

Supongamos que había que colorear los bordes de una gráfica no dirigida para que por cada vértice, los bordes a los que está conectada tengan diferentes colores. ¿Cómo se puede transformar este problema en un problema de coloración de vértices?

Contestar: Dibuja una gráfica con un vértice por cada arista, Si dos aristas en la gráfica original se encuentran en el mismo vértice, entonces dibuja una arista conectando los vértices correspondientes en la nueva gráfica.

Ejercicio$\PageIndex{14}$

Supongamos que los bordes de a$K_6$ son de color rojo o azul. Demostrar que habrá ya sea un “rojo$K_3$” (un subconjunto del conjunto de vértices con tres vértices conectados por bordes rojos) o un “azul$K_3$” o ambos.
Supongamos que seis personas son seleccionadas al azar. Demostrar que o existe un subconjunto de tres de ellos con la propiedad de que dos personas cualesquiera del subconjunto puedan comunicarse en un idioma común, o existen tres personas, no dos de las cuales pueden comunicarse en un lenguaje común.

Ejercicio$\PageIndex{15}$

Dejar$d$ ser un entero positivo, y dejar$a_1, a_2, \dots a_d$ ser enteros positivos mayores o iguales a dos. El gráfico de malla$M(a_1,a_2,\dots,a_d)$ tiene vértices de la forma$x=(x_1, x_2,\dots, x_d)$ donde$1 \leq x_i \leq a_i\text{.}$ Dos vértices$x$ y$y$ son adyacentes si y solo si$\sum_{i=1}^{d}{\lvert x_i-y_i \rvert} = 1\text{.}$ En otras palabras, dos vértices adyacentes deben diferir en una sola coordenada y en una diferencia de 1.

¿Cuál es el número cromático de$M(a_1,a_2,\dots,a_d)\text{?}$
¿Para$(a_1, a_2)$ qué parejas$M(a_1, a_2)$ tiene un circuito hamiltoniano?
¿Para qué triples$(a_1, a_2, a_3)$$M(a_1, a_2, a_3)$ tiene un circuito hamiltoniano?

Lectura adicional

[1] Wilson, R., Basta con cuatro colores - Cómo se resolvió el problema del mapa Princeton, NJ: Princeton U. Press, 2013.