12.3: Una introducción a los espacios vectoriales

Última actualización
Guardar como PDF

Page ID: 117132

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Motivación para el estudio de los espacios vectoriales

Cuando encontramos varios tipos de matrices en el Capítulo 5, se hizo evidente que un tipo particular de matriz, la matriz diagonal, era mucho más fácil de usar en cálculos. Por ejemplo, si$A =\left( \begin{array}{cc} 2 & 1 \\ 2 & 3 \\ \end{array} \right)\text{,}$ entonces se$A^5$ puede encontrar, pero su cómputo es tedioso. Si$D =\left( \begin{array}{cc} 1 & 0 \\ 0 & 4 \\ \end{array} \right)$ entonces

\ begin {ecuación*} D^5 =\ left (\ begin {array} {cc} 1 & 0\\ 0 & 4\\\ end {array}\ right) ^5=\ left (\ begin {array} {cc} 1^5 & 0\\ 0 & 4^5\\ end {array}\\ right) =\ left (\ begin {array} {cc} 1 & 0\ 0 & 1024\\\ end {array}\ derecha)\ end {ecuación*}

Incluso cuando se le presenta una matriz no diagonal, veremos que a veces es posible hacer un poco de trabajo para poder trabajar con una matriz diagonal. Este proceso se llama diagonalización.

En una variedad de aplicaciones es beneficioso poder diagonalizar una matriz. En esta sección investigaremos qué significa esto y consideraremos algunas aplicaciones. Para entender cuándo se puede realizar el proceso de diagonalización, es necesario desarrollar varios de los conceptos subyacentes del álgebra lineal.

Espacios Vectoriales

A estas alturas, te das cuenta de que los matemáticos tienden a generalizar. Una vez que hemos encontrado algo “bueno”, algo que es útil, lo aplicamos a tantos conceptos diferentes como sea posible. Al hacerlo, frecuentemente encontramos que los “diferentes conceptos” no son realmente diferentes sino que solo se ven diferentes. Cuatro frases en cuatro idiomas diferentes pueden parecer diferentes, pero cuando se traducen a un idioma común, muy bien podrían expresar exactamente la misma idea.

Al principio del desarrollo de las matemáticas, el concepto de vector condujo a una variedad de aplicaciones en física e ingeniería. Ciertamente podemos imaginar vectores, o “flechas”, en el$x y-\textrm{ plane}$ e incluso en el espacio tridimensional. ¿Tiene sentido hablar de vectores en el espacio de cuatro dimensiones, en el espacio de diez dimensiones, o en cualquier otra situación matemática? Si es así, ¿cuál es la esencia de un vector? ¿Es su forma o las reglas que sigue? La forma en dos o tres espacios es solo una imagen, o interpretación geométrica, de un vector. La esencia son las reglas, o propiedades, deseamos que los vectores sigan para poder manipularlos algebraicamente. Lo que sigue es una definición de lo que se llama un espacio vectorial. Es una lista de todas las propiedades esenciales de los vectores, y es la definición básica de la rama de las matemáticas llamada álgebra lineal.

Definición$\PageIndex{1}$: Vector Space

Dejar$V$ ser cualquier conjunto no vacío de objetos. Definir sobre$V$ una operación, llamada suma, para dos elementos cualesquiera$\vec{x}, \vec{y} \in V\text{,}$ y denotar esta operación por$\vec{x}+ \vec{y}\text{.}$ Dejar que la multiplicación escalar se defina para un número real$a \in \mathbb{R}$ y cualquier elemento$\vec{x}\in V$ y denotar esta operación por$a \vec{x}\text{.}$ El conjunto$V$ junto con operaciones de suma y multiplicación escalar se llama un espacio vectorial sobre$\mathbb{R}$ si lo siguiente se mantiene para todos$\vec{x}, \vec{y}, \vec{z}\in V$, y$a,b \in \mathbb{R}\text{:}$

$\displaystyle \vec{x}+ \vec{y}= \vec{y}+ \vec{x}$
$\displaystyle \left(\vec{x}+ \vec{y}\right)+ \vec{z}= \vec{x}+\left( \vec{y}+\vec{z}\right)$
Existe un vector$\vec{0}\in V\text{,}$ tal que$\vec{x}+\vec{0} = \vec{x}$ para todos$x \in V\text{.}$
Por cada vector$\vec{x}\in V\text{,}$ existe un vector único$-\vec{x}\in V\text{,}$ tal que$-\vec{x} +\vec{x}= \vec{0}\text{.}$

Estas son las principales propiedades asociadas a la operación de adición. Se pueden resumir diciendo que$[V; +]$ es un grupo abeliano.

Las siguientes cuatro propiedades están asociadas con la operación de multiplicación escalar y cómo se relaciona con la adición de vectores.

$\displaystyle a\left(\vec{x}+ \vec{y} \right) =a \vec{x}+a \vec{y}$
$\displaystyle (a +b)\vec{x}= a \vec{x} + b \vec{x}$
$\displaystyle a \left(b \vec{x}\right) = (a b)\vec{x}$
$1\vec{x} = \vec{x}\text{.}$

En un espacio vectorial es común llamar a los elementos de$V$ vectores y a los de los$\mathbb{R}$ escalares. Los espacios vectoriales sobre los números reales también se denominan espacios vectoriales reales.

Ejemplo$\PageIndex{1}$: A Vector Space of Matrices

Dejar$V = M_{2\times 3}(\mathbb{R})$ y dejar que las operaciones de suma y multiplicación escalar sean las operaciones habituales de suma y multiplicación escalar en matrices. Entonces$V$ junto con estas operaciones es un verdadero espacio vectorial. Se recomienda encarecidamente al lector verificar la definición de este ejemplo antes de continuar (ver Ejercicio$\PageIndex{3}$ de esta sección). Tenga en cuenta que podemos llamar a los elementos de$M_{2\times 3}(\mathbb{R})$ vectores aunque no sean flechas.

Ejemplo$\PageIndex{2}$: The Vector Space $\mathbb{R}^{2}$

Vamos$\mathbb{R}^2 = \left\{\left(a_1, a_2 \right) \mid a_1,a_2 \in \mathbb{R}\right\}\text{.}$ Si definimos suma y multiplicación escalar de la manera natural, es decir, como lo haríamos en$1\times 2$ matrices, entonces$\mathbb{R}^2$ es un espacio vectorial sobre$\mathbb{R}\text{.}$ Ver Ejercicio$\PageIndex{4}$ de esta sección.

En este ejemplo, tenemos el “bonus” de que podemos ilustrar geométricamente el concepto algebraico. En matemáticas, un “bono geométrico” no siempre ocurre y no es necesario para el desarrollo o aplicación del concepto. Sin embargo, las ilustraciones geométricas son bastante útiles para ayudarnos a comprender conceptos y deben ser utilizadas siempre que estén disponibles.

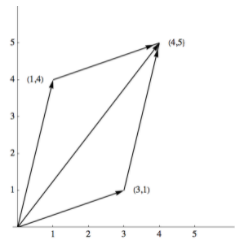$clipboard_ea75e875ee4169edb43bea84a560c0e8c.png$ Figura$\PageIndex{1}$: Suma de dos vectores en$\mathbb{R}^{2}$

Consideremos algunas ilustraciones del espacio vectorial$\mathbb{R}^2\text{.}$ Let$\vec{x}= (1, 4)$ e$\vec{y} = (3, 1)\text{.}$ Ilustramos el vector$\left(a_1, a_2\right)$ como un segmento de línea dirigida, o “flecha”, del punto$(0, 0)$ al punto$\left(a_1, a_2\right)\text{.}$ Los vectores$\vec{x}$ y$\vec{y}$ son como se muestra en la Figura$\PageIndex{1}$ junto con $\vec{x}+ \vec{y} = (1, 4) + (3, 1) = (4, 5)\text{.}$El vector$2 \vec{x} = 2(1, 4) = (2, 8)$ es un vector en la misma dirección que$\vec{x}\text{,}$ pero con el doble de su longitud.

Nota$\PageIndex{1}$

La convención común es usar esas letras en negritas hacia el final del alfabeto para los vectores, mientras que las letras al principio del alfabeto son escalares.
Una notación alternativa común para vectores es colocar una flecha alrededor de una variable para indicar que es un vector como este:$\overset{\rightharpoonup }{x}\text{.}$
El vector$\left(a_1,a_2,\ldots ,a_n\right)\in \mathbb{R}^n$ se conoce como una$n$ -tupla.
Para aquellos familiarizados con el cálculo vectorial, estamos expresando el vector$x = a_1 \boldsymbol{\hat{\textbf{i}}}+ a_2 \boldsymbol{\hat{\textbf{j}}} + a_3 \boldsymbol{\hat{\textbf{k}}} \in \mathbb{R}^3$ como$\left(a_1,a_2,a_3\right)\text{.}$ Esto nos permite discutir vectores$\mathbb{R}^n$ en una notación mucho más simple.

En muchas situaciones$V$ se da un espacio vectorial y nos gustaría describir todo el espacio vectorial por el menor número de vectores de referencia esenciales. Un ejemplo de ello es la descripción$\mathbb{R}^2\text{,}$ del$x y$ plano -plano, a través de los$y$ ejes$x$ y. Nuevamente nuestros conceptos deben ser de naturaleza algebraica por lo que no estamos restringidos únicamente a consideraciones geométricas.

Definición$\PageIndex{2}$: Linear Combination

Un vector$\pmb{ y}$ en el espacio vectorial$V$ (over$\mathbb{R}$) es una combinación lineal de los vectores$\vec{x}_1\text{,}$$\vec{x}_2, \ldots\text{,}$$\vec{x}_n$ si existen escalares de$\mathbb{R}$ tal$a_1,a_2,\ldots ,a_n$ manera que$\vec{y} = a_1\vec{x}_1+ a_2\vec{x}_2+\ldots +a_n\vec{x}_n$

Ejemplo$\PageIndex{3}$: A Basic Example

El vector$(2, 3)$ in$\mathbb{R}^2$ es una combinación lineal de los vectores$(1, 0)$ y$(0, 1)$ desde$(2, 3) = 2(1, 0) + 3(0, 1)\text{.}$

Ejemplo$\PageIndex{4}$: A Little Less Obvious Example

Demostrar que el vector$(4,5)$ es una combinación lineal de los vectores (3, 1) y (1, 4).

Por la definición debemos demostrar que existen escalares$a_1$ y$a_2$ tales que:

\ begin {ecuación*}\ begin {array} {ccc}\ begin {split} (4,5) &= a_1 (3, 1) + a_2 (1, 4)\\ & =\ left (3a_1+ a_2, a_1+4a_2\ right)\ end {split} &\ Rightarrow &\ begin {array} {c} 3a_1+ a_2 =4\ a_1+ 4a_2 =5\\\ final {matriz}\\\\\ final {matriz}\ final {ecuación*}

Este sistema tiene la solución$a_1=1\text{,}$$a_2=1\text{.}$

De ahí que si reemplazamos$a_1$ y$a_2$ ambos por 1, entonces los dos vectores (3, 1) y (1, 4) producen, o generan, el vector (4,5). Por supuesto, si reemplazamos$a_1$ y$a_2$ por diferentes escalares, podemos generar más vectores a partir de$\mathbb{R}^2\text{.}$ If, por ejemplo,$a _1 = 3$ y$a_2 = -2\text{,}$ luego

\ begin {ecuación*} a_1 (3, 1) + a_2 (1, 4) = 3 (3, 1) + (-2) (1,4) = (9, 3) + (-2, -8) = (7, -5)\ final {ecuación*}

Serán los vectores$(3, 1)$ y$(1,4)$ generaremos cualquier vector que escojamos en$\mathbb{R}^2\text{?}$ Para ver si esto es así, dejamos$\left(b_1,b_2\right)$ ser un vector arbitrario en$\mathbb{R}^2$ y ver si siempre podemos encontrar escalares$a_1$ y$a_2$ tal que$a_1(3, 1) + a_2 (1, 4)= \left(b_1,b_2\right)\text{.}$ Esto equivale a resolver el siguiente sistema de ecuaciones:

\ begin {ecuación*}\ begin {array} {c} 3a_1+ a_2 =b_1\\ a_1+4a_2 =b_2\\\ end {array}\ end {ecuación*}

que siempre tiene soluciones para$a_1$ y$a_2$, independientemente de los valores de los números reales$b_1$ y$b_2\text{.}$ ¿Por qué? Formalizamos esta situación en una definición:

Definición$\PageIndex{3}$: Generation of a Vector Space

Let$\left\{\vec{x}_1,\vec{x}_2, \ldots ,\vec{x}_n\right\}$ be a set of vectors in a vector space$V$ over$\mathbb{R}\text{.}$ This set is said to generate, or span,$V$ if, for any given vector$\vec{y} \in V\text{,}$ we can always find scalars$a_1\text{,}$$a_2, \ldots\text{,}$$a_n$ such that$\vec{y} = a_1 \vec{x}_1+a_2 \vec{x}_2+\ldots +a_n \vec{x}_n\text{.}$ A set that generate a el espacio vectorial se denomina conjunto generador.

Ahora damos una interpretación geométrica de los ejemplos anteriores.

Sabemos que el sistema de coordenadas estándar,$x$ eje y$y$ eje, fueron introducidos en álgebra básica con el fin de describir todos los puntos del$xy$ plano algebraicamente. También es bastante claro que para describir cualquier punto en el plano necesitamos exactamente dos ejes.

Podemos configurar un nuevo sistema de coordenadas de la siguiente manera. Dibuja el vector$(3, 1)$ y un eje desde el origen hasta (3, 1) y etiquetarlo como$x'$ eje. También dibuja el vector$(1,4)$ y un eje desde el origen$(1,4)$ hasta que se etiquetará el$y'$ eje. Dibujar la cuadrícula de coordenadas para el eje, es decir, líneas paralelas, y dejar que las longitudes unitarias de este “nuevo” plano sean las longitudes de los vectores respectivos,$(3, 1)$ y para$(1, 4)\text{,}$ que obtengamos Figura$\PageIndex{2}$.

A partir de Ejemplo$\PageIndex{4}$ y Figura$\PageIndex{2}$, vemos que cualquier vector en el plano puede describirse usando los$xy$ ejes estándar o nuestros nuevos$x'y'$ ejes. De ahí que la posición que tenía el nombre$(3,1)$ en referencia a los ejes estándar tenga el nombre$(1,0)$ con respecto a los$x'y'$ ejes, o, en la fraseología del álgebra lineal, las coordenadas del punto$(1,4)$ con respecto a los$x'y'$ ejes son$(1, 0)\text{.}$

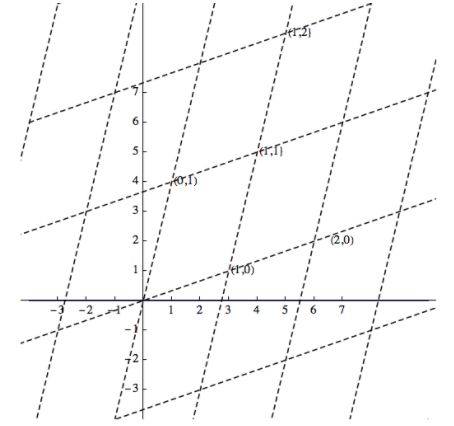$clipboard_e5999b24b744f85a15dd0c8f46c48b5d3.png$ Figura$\PageIndex{2}$: Dos juegos de ejes para el plano

Ejemplo$\PageIndex{5}$: One Point, Two Position Descriptions

De Ejemplo$\PageIndex{4}$ encontramos que si elegimos$a_1=1$ y$a_2=1\text{,}$ luego los dos vectores$(3, 1)$ y$(1,4)$ generamos el vector$(4,5)\text{.}$ Otra interpretación geométrica de este problema es que las coordenadas de la posición$(4,5)$ con respecto a los$x'y'$ ejes de la Figura $\PageIndex{2}$es$(1, 1)\text{.}$ En otras palabras, una posición en el plano tiene el nombre$(4,5)$ en referencia a los$xy$ -ejes y la misma posición tiene el nombre$(1, 1)$ en referencia a los$x'y'$ ejes.

De lo anterior, queda claro que podemos utilizar diferentes ejes para describir puntos o vectores en el plano. No importa qué elección usemos, queremos poder describir cada posición de una manera única. Este no es el caso en la Figura$\PageIndex{3}$. Cualquier punto en el plano podría describirse a través de los$x'y'$ ejes, los$x'z'$ ejes o los$y'z'$ ejes. Por lo tanto, en este caso, un solo punto tendría tres nombres diferentes, una situación muy confusa.

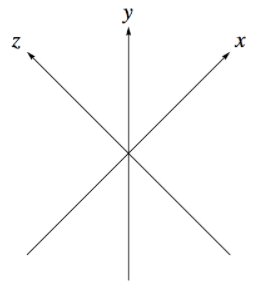$clipboard_e7ba5549288635f47e8efc58b1d818063.png$ Figura$\PageIndex{3}$: Tres ejes en un plano

Formalizamos las nuestras observaciones en los ejemplos anteriores en dos definiciones y un teorema.

Definición$\PageIndex{4}$: Linear Independence/Linear Dependence

Un conjunto de vectores$\left\{\vec{x}_1,\vec{x}_2, \ldots ,\vec{x}_n\right\}$ de un espacio vectorial real$V$ es linealmente independiente si la única solución a la ecuación$a_1 \vec{x}_1+a_2 \vec{x}_2+\ldots +a_n \vec{x}_n= \vec{0}$ es$a_1 = a_2 = \ldots = a_n = 0\text{.}$ De lo contrario, el conjunto se denomina conjunto linealmente dependiente.

Definición$\PageIndex{5}$: Basis

Un conjunto de vectores$B=\left\{\vec{x}_1,\vec{x}_2, \ldots ,\vec{x}_n\right\}$ es una base para un espacio vectorial$V$ si:

$B$genera$V\text{,}$ y
$B$es linealmente independiente.

Teorema$\PageIndex{1}$: The Fundamental Property of a Basis

Si$\left\{\vec{x}_1,\vec{x}_2, \ldots ,\vec{x}_n\right\}$ es una base para un espacio vectorial V sobre$\mathbb{R}\text{,}$ entonces cualquier vector$y \in V$ puede expresarse de manera única como una combinación lineal de$\vec{x}_i\textrm{'s}\text{.}$

Prueba

Supongamos que$\left\{\vec{x}_1,\vec{x}_2, \ldots ,\vec{x}_n\right\}$ es una base para$V$ más$\mathbb{R}\text{.}$ Debemos probar dos hechos:

cada vector se$y \in V$ puede expresar como una combinación lineal de los$\vec{x}_i\textrm{'s}\text{,}$ y
cada una de esas expresiones es única.

La primera parte es trivial ya que una base, por su definición, debe generar todos$V\text{.}$

La prueba de la parte 2 es un poco más difícil. Seguimos el enfoque estándar para cualquier hecho de singularidad. $y$Sea cualquier vector adentro$V$ y asuma que hay dos formas diferentes de expresar$y\text{,}$ a saber

\ comenzar {ecuación*} y = a_1\ vec {x} _1+a_2\ vec {x} _2+\ lpuntos +a_n\ vec {x} _n\ final {ecuación*}

\ begin {ecuación*} y = b_1\ vec {x} _1+b_2\ vec {x} _2+\ lpuntos +b_n\ vec {x} _n\ end {ecuación*}

donde al menos una$a_i$ es diferente de la correspondiente$b_i\text{.}$ Luego igualando estas dos combinaciones lineales obtenemos

\ begin {ecuación*} a_1\ vec {x} _1+a_2\ vec {x} _2+\ lpuntos +a_n\ vec {x} _n=b_1\ vec {x} _1+b_2\ vec {x} _2+\ lpuntos +b_n\ vec {x} _n\ final {ecuación*}

para que

\ begin {ecuación*}\ izquierda (a_1-b_1\ derecha)\ vec {x} _1+\ izquierda (a_2-b_2\ derecha)\ vec {x} _2+\ ldots +\ izquierda (a_n-b_n\ derecha)\ vec {x} _n=\ vec {0}\ end {ecuación*}

Ahora una observación crucial: dado que la$\vec{x}_i's$ forma un conjunto linealmente independiente, la única solución a la ecuación anterior es que cada uno de los coeficientes debe ser igual a cero, así$a_i-b_i=0$ para$i = 1, 2, \ldots ,n\text{.}$ De ahí$a_i=b_i\text{,}$ para todos$i\text{.}$ Esto contradice nuestra suposición de que al menos uno$a_i$ es diferente al correspondiente$b_i\text{,}$ por lo que cada vector se$\vec{y} \in V$ puede expresar de una y sólo una manera.

Este teorema, junto con los ejemplos anteriores, nos da una idea clara de la importancia de la independencia lineal, es decir, la singularidad en la representación de cualquier vector.

Ejemplo$\PageIndex{6}$: Another Basis for $\mathbb{R}^{2}$

Demostrar que$\{(1, 1), (-1, 1)\}$ es una base para$\mathbb{R}^2$ más$\mathbb{R}$ y explicar lo que esto significa geométricamente.

Primero mostramos que los vectores$(1, 1)$ y$(-1, 1)$ generar todos$\mathbb{R}^2\text{.}$ Podemos hacer esto imitando Ejemplo$\PageIndex{4}$ y dejarlo en manos del lector (ver Ejercicio$\PageIndex{10}$ de esta sección). En segundo lugar, debemos demostrar que el conjunto es linealmente independiente.

Dejemos$a_1$ y$a_2$ sean escalares tales que$a_1 (1, 1) + a_2 (-1, 1) = (0, 0)\text{.}$ Debemos demostrar que la única solución a la ecuación es esa$a_1$ y ambos$a_2$ deben ser iguales a cero. La ecuación anterior se convierte en$\left(a_1- a_2 , a_1 + a_2 \right) = (0, 0)$ la que nos da el sistema

\ begin {ecuación*}\ begin {array} {c} a_1 - a_ {2} =0\\ a_1 + a_2=0\\ end {array}\ end {ecuación*}

La matriz aumentada de este sistema se reduce de tal manera que la única solución es la trivial de todos los ceros:

\ begin {ecuación*}\ left (\ begin {array} {cc|c} 1 & -1 & 0\\ 1 & 0 & 0\\ end {array}\ right)\ longrightarrow\ left (\ begin {array} {cc|c} 1 & 0 & 0\\ 0 & 1 & 0\\ end {array}\ right)\ textrm {}\ Rightarrow\ tderecha\ textrm {}\ fila derecha\ extrm {} a_1 = a_2 =0\ final {ecuación*}

Por lo tanto, el conjunto es linealmente independiente.

Para explicar los resultados geométricamente, anote a través del Ejercicio 12, parte a, que las coordenadas de cada vector se$\vec{y} \in \mathbb{R}^2$ pueden determinar de manera única utilizando los vectores (1,1) y (-1, 1). El concepto de dimensión es bastante obvio para aquellos espacios vectoriales que tienen una interpretación geométrica inmediata. Por ejemplo, la dimensión de$\mathbb{R}^2$ es dos y la de$\mathbb{R}^3$ es tres. ¿Cómo podemos definir algebraicamente el concepto de dimensión para que la definición resultante se correlacione con la de$\mathbb{R}^2$ y$\mathbb{R}^3\text{?}$ Primero necesitamos un teorema, que vamos a exponer sin pruebas?

Teorema$\PageIndex{2}$: Basis Size is Constant

Si$V$ es un espacio vectorial con una base que contiene$n$ elementos, entonces todas las bases de$V$ contienen$n$ elementos.

Definición $\PageIndex{6}$: Dimension of a Vector Space

Dejar$V$ ser un espacio vectorial encima$\mathbb{R}$ con base$\left\{\vec{x}_1,\vec{x}_2, \ldots ,\vec{x}_n\right\}\text{.}$ Entonces la dimensión de$V$ es$n\text{.}$ Utilizamos la notación$\dim V = n$ para indicar que$V$ es$n$ -dimensional.

Ejercicios

Ejercicio$\PageIndex{1}$

Si$a = 2\text{,}$$b = -3\text{,}$$A=\left( \begin{array}{ccc} 1 & 0 & -1 \\ 2 & 3 & 4 \\ \end{array} \right)\text{,}$$B=\left( \begin{array}{ccc} 2 & -2 & 3 \\ 4 & 5 & 8 \\ \end{array} \right)\text{,}$ y$C=\left( \begin{array}{ccc} 1 & 0 & 0 \\ 3 & 2 & -2 \\ \end{array} \right)$ verificar que todas las propiedades de la definición de un espacio vectorial son verdaderas para$M_{2\times 3}(\mathbb{R})$ con estos valores.

Ejercicio$\PageIndex{2}$

Dejar$a = 3\text{,}$$b = 4\text{,}$$\vec{x}\pmb = (-1, 3)\text{,}$$\vec{y} = (2, 3)\text{,}$ y$\vec{z} = (1, 0)\text{.}$ verificar que todas las propiedades de la definición de un espacio vectorial son verdaderas$\mathbb{R}^2$ para estos valores.

Ejercicio$\PageIndex{3}$

Verificar que$M_{2\times 3}(\mathbb{R})$ es un espacio vectorial sobre$\mathbb{R}\text{.}$ ¿Cuál es su dimensión?
Se acabó$M_{m\times n}(\mathbb{R})$ un espacio vectorial$\mathbb{R}\text{?}$ Si es así, ¿cuál es su dimensión?

Contestar: La dimensión de$M_{2\times 3}(\mathbb{R})$ es 6 y sí, también$M_{m\times n}(\mathbb{R})$ es un espacio vectorial de dimensión$m \cdot n\text{.}$ Una base para$M_{m\times n}(\mathbb{R})$ es$\{A_{ij} \mid 1 \leq i \leq m, 1 \leq j \leq n\}$ donde$A_{ij}$ está la$m\times n$ matriz con entradas todas iguales a cero excepto para en fila$i\text{,}$ columna$j$ donde la entrada es 1.

Ejercicio$\PageIndex{4}$

Verificar que$\mathbb{R}^2$ es un espacio vectorial sobre$\mathbb{R}\text{.}$
Es$\mathbb{R}^n$ un espacio vectorial$\mathbb{R}$ para cada entero positivo$n\text{?}$

Ejercicio$\PageIndex{5}$

$P^3= \left\{a_0 + a_1x + a_2x^2 + a_3x^3 \mid a_0,a_1,a_2,a_3\in \mathbb{R}\right\}\text{;}$Que sea,$P^3$ es el conjunto de todos los polinomios en$x$ tener coeficientes reales con grado menor o igual a tres. Verificar que$P^3$ es un espacio vectorial sobre$\mathbb{R}\text{.}$ ¿Cuál es su dimensión?

Ejercicio$\PageIndex{6}$

Para cada uno de los siguientes, exprese el vector$\pmb{y}$ como una combinación lineal de los vectores$x_1$ y$x_2\text{.}$

$\vec{y} = (5, 6)\text{,}$$\vec{x}_1 =(1, 0)\text{,}$y$\vec{x}_2 = (0, 1)$
$\vec{y} = (2, 1)\text{,}$$\vec{x}_1 =(2, 1)\text{,}$y$\vec{x}_2 = (1, 1)$
$\vec{y} = (3,4)\text{,}$$\vec{x}_1 = (1, 1)\text{,}$y$\vec{x}_2 = (-1, 1)$

Ejercicio$\PageIndex{7}$

Expresar el vector$\left( \begin{array}{cc} 1 & 2 \\ -3 & 3 \\ \end{array} \right)\in M_{2\times 2}(\mathbb{R})\text{,}$ como una combinación lineal de$\left( \begin{array}{cc} 1 & 1 \\ 1 & 1 \\ \end{array} \right)\text{,}$$\left( \begin{array}{cc} -1 & 5 \\ 2 & 1 \\ \end{array} \right)\text{,}$$\left( \begin{array}{cc} 0 & 1 \\ 1 & 1 \\ \end{array} \right)$ y$\left( \begin{array}{cc} 0 & 0 \\ 0 & 1 \\ \end{array} \right)$

Contestar

Si las matrices son nombradas$B\text{,}$$A_1\text{,}$$A_2$,$A_3\text{,}$ y$A_4$, entonces

\ begin {ecuación*} B =\ frac {8} {3} A_1 +\ frac {5} {3} A_2+\ frac {-5} {3} A_3+\ frac {23} {3} A_4\ end {ecuación*}

Ejercicio$\PageIndex{8}$

Expresar el vector$x^3-4x^2+3\in P^3$ como una combinación lineal de los vectores 1,$x\text{,}$$x^2$, y$x^3\text{.}$

Ejercicio$\PageIndex{9}$

Mostrar que el conjunto$\left\{\vec{x}_1,\vec{x}_2\right\}$ genera$\mathbb{R}^2$ para cada una de las partes en Ejercicio$\PageIndex{6}$ de esta sección.
Demostrar que$\left\{\vec{x}_1,\vec{x}_2,\vec{x}_3\right\}$ genera$\mathbb{R}^2$ dónde$\vec{x}_1= (1, 1)\text{,}$$\vec{x}_2= (3,4)\text{,}$ y$\vec{x}_3 = (-1, 5)\text{.}$
Crear un conjunto de cuatro o más vectores que genere$\mathbb{R}^2\text{.}$
Cuál es el menor número de vectores necesarios para generar$\mathbb{R}^2\text{?}$$\mathbb{R}^n\text{?}$
Mostrar que el conjunto
\ begin {ecuation*}\ {A_1, A_2, A_3, A_4\} =\ {\ left (\ begin {array} {cc} 1 & 0\\\ 0 & 0\\ end {array}\ right),\ left (\ begin {array} {cc} 0 & 1\\ 0 & 0\\\ end {array}\ right),\ left (begin\ {array} {cc} 0 & 0\\ 1 & 0\\\ end {array}\ derecha),\ left (\ begin { array} {cc} 0 & 0\\ 0 & 1\\\ end {array}\ derecha)\}\ end {ecuación*}
genera$M_{2\times 2}(\mathbb{R})$
Mostrar que$\left\{1,x,x^2 ,x^3\right\}$ genera$P^3\text{.}$

Contestar

Si$x_1 = (1, 0)\text{,}$$x_2= (0, 1)\text{,}$ y$y = \left(b_1, b_2\right)\text{,}$ luego$y = b_1x_1+b_2x_2\text{.}$ Si$x_1 = (3, 2)\text{,}$$x_2= (2,1)\text{,}$ y$y = \left(b_1, b_2\right)\text{,}$ luego$y =\left(- b_1+2b_2\right)x_1+\left(2b_1-3b_2\right)x_2\text{.}$
Si$y = \left(b_1, b_2\right)$ hay algún vector en$\mathbb{R}^2$, entonces$y =\left(- 3b_1+4b_2\right)x_1+\left(-b_1+b_2\right)x_2 + (0)x_3$
Una solución es agregar cualquier vector (s) a$x_1\text{,}$$x_2\text{,}$ y$x_3$ de la parte b.
2,$n$
$\displaystyle \left( \begin{array}{cc} x & y \\ z & w \\ \end{array} \right)= x A_1+y A_2+ z A_3+ w A_4$
$a_0+a_1x + a_2x^2+ a_3x^3=a_0(1)+a_1(x) + a_2\left(x^2\right)+ a_3\left(x^3\right)\text{.}$

Ejercicio$\PageIndex{10}$

Ejemplo completo$\PageIndex{6}$ mostrando que$\{(1, 1), (-1, 1)\}$ genera$\mathbb{R}^2\text{.}$

Ejercicio$\PageIndex{11}$

Demostrar que$\{(4, 1), (1, 3)\}$ es una base para$\mathbb{R}^2$ más$\mathbb{R}\text{.}$
Demostrar que$\{(1, 0), (3, 4)\}$ es una base para$\mathbb{R}^2$ más$\mathbb{R}\text{.}$
Demostrar que$\{(1,0, -1), (2, 1, 1), (1, -3, -1)\}$ es una base para$\mathbb{R}^3$ más$\mathbb{R}\text{.}$
Demostrar que los conjuntos en Ejercicio$\PageIndex{9}$, partes e y f, forman bases de los respectivos espacios vectoriales.

Contestar

El conjunto es linealmente independiente: dejar$a$ y$b$ ser escalares tal que$a(4, 1) + b(1, 3) = (0, 0)\text{,}$ entonces el$4a + b = 0\textrm{ and } a + 3b= 0$ cual tiene$a = b = 0$ como únicas soluciones. El conjunto genera todos$\mathbb{R}^2\text{:}$ let$(a, b)$ ser un vector arbitrario en$\mathbb{R}^2$. Queremos demostrar que siempre podemos encontrar escalares$\beta _1$ y$\beta _2$ tal que$\beta _1(4, 1) +\beta _2 (1,3) = (a, b)\text{.}$ Esto equivale a encontrar escalares tales que$4\beta _1 +\beta _2 = a$ y$\beta _1 + 3\beta _2 = b\text{.}$ Este sistema tiene una solución única$\beta _1=\frac{3a - b}{11}\text{,}$ y$\beta _2= \frac{4b-a}{11}\text{.}$ por lo tanto, el conjunto genera$\mathbb{R}^2\text{.}$

Ejercicio$\PageIndex{12}$

Determina las coordenadas de los puntos o vectores$(3, 4)\text{,}$$(-1, 1)\text{,}$ y$(1, 1)$ con respecto a la base$\{(1, 1),(-1, 1)\}$ de$\mathbb{R}^2\text{.}$ Interpreta tus resultados geométricamente.
Determinar las coordenadas de los puntos o vector$(3, 5, 6)$ con respecto a la base$\{(1, 0, 0), (0, 1, 0), (0, 0, 1)\}\text{.}$ Explicar por qué esta base se llama la base estándar para$\mathbb{R}^3\text{.}$

Ejercicio$\PageIndex{13}$

Let$\vec{y}_1= (1,3, 5, 9)\text{,}$$\vec{y}_2= (5,7, 6, 3)\text{,}$ and$c = 2\text{.}$ Find$\vec{y}_1+\vec{y}_2$ y$c \vec{y}_1\text{.}$
Deja$f_1(x) = 1 + 3x + 5x^2 + 9x^3$,$f_2(x)=5 + 7x+6x^2+3x^3$ y$c = 2\text{.}$ Encuentra$f_1(x)+f_2(x)$ y$c f_1(x)\text{.}$
Let$A =\left( \begin{array}{cc} 1 & 3 \\ 5 & 9 \\ \end{array} \right)\text{,}$$B=\left( \begin{array}{cc} 5 & 7 \\ 6 & 3 \\ \end{array} \right)\text{,}$ and$c=2\text{.}$ Find$A + B$ y$c A\text{.}$
¿Son los espacios vectoriales$\mathbb{R}^4$,$P^3$ e$M_{2\times 2}(\mathbb{R})$ isomórficos entre sí? Discutir con referencia a partes anteriores de este ejercicio.

Contestar

La respuesta a la última parte es que los tres espacios vectoriales son todos isomórficos entre sí. Una vez que haya completado la parte (a) de este ejercicio, las siguientes reglas de traducción le darán la respuesta a las partes (b) y (c),

\[(a,b,c,d)\leftrightarrow \left(\begin{array}{cc}a&b\\c&d\end{array}\right)\leftrightarrow a+bx+cx^2+dx^2\nonumber\]