14.1: Monoides

Última actualización
Guardar como PDF

Page ID: 117137

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Recordemos que en la Sección 11.2 introdujimos sistemas llamados monoides. Aquí está la definición formal.

Definición$\PageIndex{1}$: Monoid

Un monoide es un conjunto$M$ junto con una operación binaria$*$ con las propiedades

$*$es asociativo:$\forall a,b,c \in M\text{,}$$(a*b)*c=a*(b*c)$ y
$*$tiene una identidad en$M\text{:}$$\exists e\in M$ tal que$\forall a \in M\text{,}$$a*e=e*a=a$

Nota$\PageIndex{1}$

Dado que los requisitos para un grupo contienen los requisitos para un monoide, cada grupo es un monoide.

Ejemplo$\PageIndex{1}$: Some Monoids

El conjunto de potencia de cualquier conjunto junto con cualquiera de las operaciones de intersección, unión o diferencia simétrica es un monoide.
El conjunto de enteros,$\mathbb{Z}\text{,}$ con multiplicación, es un monoide. Con adición, también$\mathbb{Z}$ es un monoide.
El conjunto de$n\times n$ matrices sobre los enteros,$M_n(\mathbb{Z})\text{,}$$n\geq 2\text{,}$ con multiplicación matricial, es un monoide. Esto se desprende del hecho de que la multiplicación matricial es asociativa y tiene una identidad,$I_n\text{.}$ Este es un ejemplo de monoide no conmutativo ya que existen matrices,$A$ y$B\text{,}$ para el cual$A B \neq B A\text{.}$
$\left[\mathbb{Z}_n;\times_n\right],n\geqslant 2\text{,}$es un monoide con identidad 1.
Dejar$X$ ser un conjunto no vacío. El conjunto de todas las funciones de$X$ a$X\text{,}$ menudo denotadas$X^X\text{,}$ es una composición monoide sobre la función. En el Capítulo 7, vimos que la composición de funciones es asociativa. La función$i:X\to X$ definida por$i(a)=a$ es el elemento de identidad para este sistema. Si$\lvert X\rvert$ es mayor que 1 entonces es un monoide no conmutativo. Si$X$ es finito,$\left\lvert X^X\right\rvert =\lvert X\rvert ^{\lvert X\rvert }$. Por ejemplo, si$B=\{0,1\}, \left\lvert B^B\right\rvert=4\text{.}$ Las funciones$z,u,i,\textrm{ and } t,$ definidas por las gráficas de la Figura$\PageIndex{1}$, son los elementos de$B^B$. Este monoide no es un grupo. ¿Sabes por qué?
Una razón por la que no$B^B$ es conmutativa es que$t \circ z \neq z \circ t$ porque$(t\circ z)(0)=t(z(0))=t(0)=1$ mientras$(z\circ t)(0)=z(t(0))=z(1)=0\text{.}$

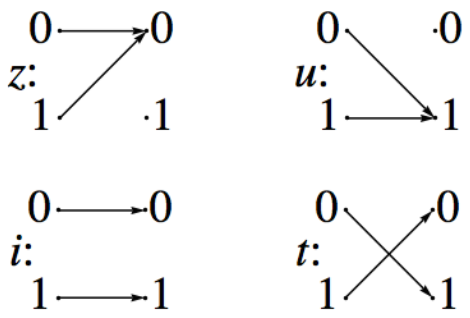$clipboard_e0e4ecd170c14b92b407fcf9e51eeb978.png$ Figura$\PageIndex{1}$: Las funciones en$B_{2}$

Prácticamente todos los conceptos grupales que se discutieron en el Capítulo 11 son aplicables a los monoides. Cuando introdujimos subsistemas, vimos que un submonoide de monoide$M$ es un subconjunto de$M\text{;}$ eso es, es un monoide con la operación de$M\text{.}$ Para probar que un subconjunto es un submonoide, se puede aplicar el siguiente teorema.

Teorema$\PageIndex{1}$: Submonoid Test

Supongamos que$[M; *]$ es un monoide y$K$ es un subconjunto no vacío de$M\text{.}$ Entonces$K$ es un submonoide de$M$ si y solo si se cumplen las dos condiciones siguientes.

Si$a,b\in K\text{,}$ entonces. $a*b\in K\text{;}$i. e.,$K$ se cierra con bajo$*\text{.}$
La identidad de$M$ pertenece a$K\text{.}$

A menudo vamos a querer discutir el submonoide más pequeño que incluye un cierto subconjunto$S$ de un monoide$M\text{.}$ Este submonoide se puede definir recursivamente por la siguiente definición.

Definición$\PageIndex{2}$: Submonoid Generated by a Set

Si$S$ es un subconjunto de monoide$[M;*]\text{,}$ el submonoide generado por$S\text{,}$$\langle S\rangle\text{,}$ se define por:.

(Base) La identidad de$M$ pertenece$\langle S\rangle\text{;}$ y$a\in S \Rightarrow a\in \langle S \rangle\text{.}$
(Recursión)$a,b\in \langle S\rangle \Rightarrow a*b\in \langle S\rangle\text{.}$

Nota$\PageIndex{2}$

Si$S=\left\{a_1,a_2,\ldots ,a_n\right\}\text{,}$ escribimos$\left\langle a_1,a_2,\ldots ,a_n\right\rangle$ en lugar de$\left\langle \left\{a_1,a_2,\ldots ,a_n\right\}\right\rangle\text{.}$

Ejemplo$\PageIndex{2}$: Some Submonoids

Un ejemplo de un submonoide de$[\mathbb{Z};+]$ es$\langle 2\rangle =\{0,2,4,6,8,\ldots \}\text{.}$
El conjunto de potencias de$\mathbb{Z}\text{,}$$\mathcal{P}(\mathbb{Z})\text{,}$ sobreunión es un monoide con identidad$\emptyset\text{.}$ Si$S=\{\{1\},\{2\},\{3\}\}\text{,}$ entonces$\langle S \rangle$ es el conjunto de potencias de$\{1,2,3\}\text{.}$ Si$S=\{\{n\}:n\in \mathbb{Z}\},$ entonces$\langle S\rangle$ es el conjunto de subconjuntos finitos de los enteros.

Como cabría esperar, dos monoides son isomórficos si y sólo si existe una regla de traducción entre ellos para que cualquier proposición verdadera en un monoide se traduzca en una proposición verdadera en el otro.

Ejemplo$\PageIndex{3}$

$M=[\mathcal{P}\{1,2,3\};\cap ]$es isomórfica a$M_2=\left[\mathbb{Z}_2^3;\cdot \right]\text{,}$ donde la operación en$M_2$ es componentwise mod 2 multiplicación. Una regla de traducción es que si$A\subseteq \{1,2,3\}\text{,}$ entonces se traduce a$\left(d_1,d_2,d_3\right)$ donde

\ begin {ecuation*} d_i=\ left\ {\ begin {array} {cc} 1 &\ textrm {if} i\ in A\\ 0 &\ textrm {if} i\ notin A\\ end {array}\\ right. \ end {ecuación*}

Dos casos de cómo funciona esta regla de traducción son:

\ begin {ecuation*}\ begin {array} {lr}\ begin {array} {c}\ {1, 2, 3\}\ quad\ textrm {es la identidad para} M_2\\ end {array} &\ begin {array} {c}\\\ {1, 2\}\ cap\ {2, 3\} =\ {2\}\\\ flecha arribaabajo\\ (1, 1, 0)\ cdot (0, 1, 1) = (0, 1, 0)\\ final {array}\\\ quad\ fin {matriz}\ texto {.} \ end {ecuación*}

Una definición más precisa de un isomorfismo monoide es idéntica a la definición de un isomorfismo grupal, Definición 11.7.2.

Ejercicios

Ejercicio$\PageIndex{1}$

Para cada uno de los subconjuntos del monoide indicado, determinar si el subconjunto es un submonoide.

$S_1=\{0,2,4,6\}$y$S_2=\{1,3,5,7\}$ en$[\mathbb{Z}_8;\times_8].$
$\{f\in \mathbb{N}^{\mathbb{N}}:f(n) \leqslant n, \forall n \in \mathbb{N}\}$y$\left\{f\in \mathbb{N}^{\mathbb{N}}:f(1)=2\right\}$ en el monoide$[\mathbb{N}^{\mathbb{N}};\circ]\text{.}$
$\{A\subseteq \mathbb{Z} \mid A \textrm{ is finite}\} \textrm{ and} \left\{A\subseteq \mathbb{Z} \mid A^c\textrm{ is} \textrm{ finite}\right\}$en$[\mathcal{P}(\mathbb{Z});\cup].$

Responder

$S_1$no es un submonoide ya$\left[\mathbb{Z}_8; \times_8\right]\text{,}$ que cuya identidad es 1, no está en$S_1\text{.}$$S_2$ es un submonoide ya que$1 \in S_2$ y$S_2$ se cierra bajo multiplicación; es decir, para todos$a, b \in S_2\text{,}$$a \times_8 b$ está en$S_2\text{.}$
La identidad de$\mathbb{N}^{\mathbb{N}}$ es la función de identidad$i:\mathbb{N}\to \mathbb{N}$ definida por$i(a) = a\text{,}$$\forall a\in \mathbb{N}\text{.}$ Si$a \in \mathbb{N}\text{,}$$i(a) = a \leq a\text{,}$ así la identidad de$\mathbb{N}^{\mathbb{N}}$ está en$S_1\text{.}$ Sin embargo, la imagen de 1 bajo cualquier función en$S_2$ es 2, y por lo tanto la identidad de no$\mathbb{N}^{\mathbb{N}}$ está en$S_2\text{,}$ tan $S_2$no es un submonoide. La composición de dos funciones cualesquiera en$S_1\text{,}$$f$ y$g\text{,}$ será una función en$S_1\text{:}$
\ begin {ecuation*}\ begin {split} (f\ circ g) (n) & = f (g (n))\ leq g (n)\ textrm {since} f\ textrm {está en} S_1\ &\ leq n\ textrm {since} g\ textrm {está en} S_1\ Rightarrow f\ circ g\ in S_1\ end {split}\ end {equation*}
y las dos condiciones de un submonoide se satisfacen y$S_1$ es un submonoide de$\mathbb{N}^{\mathbb{N}}\text{.}$
El primer conjunto es un submonoide, pero el segundo no lo es ya que el conjunto nulo tiene un complemento no finito.

Ejercicio$\PageIndex{2}$

Para cada subconjunto, describa el submonoide que genera.

$\{3\}$en$[\mathbb{Z}_{12};\times_{12}]$
$\displaystyle \{5\} \textrm{ in } [\mathbb{Z}_{25};\times_{25}]$
el conjunto de números primos en$[\mathbb{P}; \cdot ]$
$\displaystyle \{3,5\} \textrm{ in } [\mathbb{N}; +]$

Ejercicio$\PageIndex{3}$

$n \times n$matriz de números reales se llama estocástica si y sólo si cada entrada es no negativa y la suma de entradas en cada columna es 1. Demostrar que el conjunto de matrices estocásticas es una multiplicación monoide sobre matriz.

Responder

El conjunto de matrices$n \times n$ reales es un monoide bajo multiplicación matricial. Esto se desprende de las leyes del álgebra matricial en el Capítulo 5. Para demostrar que el conjunto de matrices estocásticas es un monoide sobre la multiplicación matricial, solo necesitamos mostrar que la matriz de identidad es estocástica (esto es obvio) y que el conjunto de matrices estocásticas se cierra bajo multiplicación matricial. Dejar$A$ y$B$ ser matrices$n \times n$ estocásticas.

\ begin {ecuación*} (AB) _ {i j} =\ suma _ {k=1} ^n a_ {i k} b_ {k j}\ end {ecuación*}

La suma de la$j^{\textrm{th}}$ columna es

\ begin {ecuación*}\ comenzar {dividir}\ suma_ {j=1} ^n (AB) _ {i j} & =\ suma_ {k=1} ^n a_ {1 k} b_ {k j} +\ suma_ {k=1} ^n a_ {1k} b_ {k j} +\ cdots +\ suma_ {k=1} ^n a_ {k} b_ {k j}\\ &=\ sum_ {k=1} ^n\ izquierda (a_ {1 k} b_ {k j} +a_ {1k} b_ {k j} b_ {k j} +\ cdots +a_ {n k} b_ {k j}\ derecha)\\ &=\ suma _ {k=1} ^n b_ {k j}\ izquierda (a_ {k 1} +a_ {1k} +\ cdots +a_ {n k}\ derecha)\\ &=\ suma _ {k=1} ^n b_ {k j}\ quad\ textrm {desde} A\ textrm {es estocástico}\\ & = 1\ quad\ textrm {desde} B\ textrm {es estocástico}\\\ end {split}\ end {ecuación*}

Ejercicio$\PageIndex{4}$

Un semigrupo es un sistema algebraico$[S; *]$ con el único axioma que$*$ sea asociativo en$S\text{.}$ Probar que si$S$ es un conjunto finito, entonces debe existir un elemento idempotente, es decir, un$a \in S$ tal que$a * a = a\text{.}$

Ejercicio$\PageIndex{5}$

Dejar$B$ ser un álgebra booleana y$M$ el conjunto de todas las funciones booleanas en$B\text{.}$ Let$*$ be defined on$M$ by$(f * g)(a) = f(a) \land g(a)\text{.}$ Probar que$[M;*]$ es un monoide. Construir la tabla de operaciones de$[M;*]$ para el caso de$B = B_2\text{.}$

Responder

Vamos$f,\: g,\: h∈M$, y$a∈B$.

\ comenzar {ecuación*}
\ comenzar {dividir}
((f*g) *h) (a) & = (f*g) (a)\ tierra h (a)\\
& = (f (a)\ tierra g (a))\ tierra h (a)\
& = f (a)\ tierra (g (a)\ tierra h (a)\ tierra h (a)\
& = f (a)\ tierra (g * h) (a)\\
& = ( f * (g * h)) (a)\\
\ end {split}
\ end {ecuación*}

Por lo tanto$(f∗g)∗h=f∗(g∗h)$ y$∗$ es asociativo.

La identidad para$∗$ es la función$u∈M$ donde$u(a)=1 =$ el “uno” de$B$. Si$a∈B$,$(f∗u)(a)=f(a)∧u(a)=f(a)∧1=f(a)$. Por lo tanto$f∗u=f$. De igual manera,$u∗f=f$.

Hay$2^2=4$ funciones en$M$ para$B=B_2$. Estas cuatro funciones se nombran en el texto. Ver Figura$\PageIndex{1}$. La mesa para$∗$ es

\ begin {ecuación*}
\ begin {array} {c|cccc}
* & z & i & t & u\
\ hline
z &z & z & z & z\\
i &z & i & z & z & i\\
t &z & z & t\\
u &z & i & t & u\\
\ end {array}
\ end {ecuación*}