15.1: Grupos cíclicos

Última actualización
Guardar como PDF

Page ID: 117159

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Los grupos se clasifican según su tamaño y estructura. La estructura de un grupo es revelada por un estudio de sus subgrupos y otras propiedades (por ejemplo, si es abeliano) que podrían dar una visión general de la misma. Los grupos cíclicos tienen la estructura más simple de todos los grupos.

Definición$\PageIndex{1}$: Cyclic Group

$G$El grupo es cíclico si existe$a \in G$ tal que el subgrupo cíclico generado por es$a\text{,}$$\langle a \rangle\text{,}$ igual a todos de$G\text{.}$ Eso es,$G = \{n a |n \in \mathbb{Z}\}\text{,}$ en cuyo caso$a$ se llama generador de$G\text{.}$ El lector debe tener en cuenta que la notación aditiva se utiliza para$G\text{.}$

Ejemplo$\PageIndex{1}$: A Finite Cyclic Group

$\mathbb{Z}_{12} = [\mathbb{Z}_{12}; +_{12} ]\text{,}$donde$+_{12}$ es adición módulo 12, es un grupo cíclico. Para verificar esta afirmación, todo lo que tenemos que hacer es demostrar que algún elemento de$\mathbb{Z}_{12}$ es un generador. Uno de esos elementos es 5; es decir,$\langle 5 \rangle = \mathbb{Z}_{12}\text{.}$ Un generador más obvio es 1. De hecho, 1 es un generador de cada Al$[\mathbb{Z}_n; +_n]\text{.}$ lector se le pide que demuestre que si un elemento es un generador, entonces su inversa es también un generador. Así,$-5 = 7$ y$-1 = 11$ son los otros generadores de$\mathbb{Z}_{12}\text{.}$ Los ocho elementos restantes del grupo no son generadores.

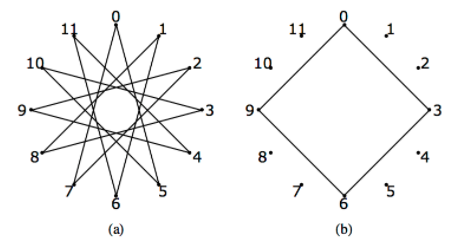$clipboard_e9f92697da347bcde751b04e8fecf8bb5.png$ Figura $\PageIndex{1}$: Copiar y Pegar Subtítulo aquí. (Copyright; autor vía fuente)

La Figura$\PageIndex{1}$ (a) es un ejemplo de “arte de cuerdas” que ilustra cómo 5 genera$\mathbb{Z}_{12}\text{.}$ Doce tachuelas se colocan uniformemente alrededor de un círculo y se numeran del 0 al 11. Una cadena se ata a tack 0, y luego se gira alrededor de cada quinta tachueta. En consecuencia, los números de las tachuelas que se alcanzan son exactamente los múltiplos ordenados de 5 módulo 12:5, 10, 3,..., 7, 0. Tenga en cuenta que si se utilizara cada séptima tachuelas, se produciría la misma obra de arte. Si se conectara cada tercera tachuelas, como en la Figura$\PageIndex{1}$ (b), el bucle resultante solo usaría cuatro tachuelas; así 3 no genera$\mathbb{Z}_{12}\text{.}$

Ejemplo$\PageIndex{2}$: The Group of Integers is Cyclic

El grupo aditivo de números enteros,$[\mathbb{Z}; +]\text{,}$ es cíclico:

\ begin {ecuación*}\ mathbb {Z} =\ langle 1\ rangle =\ {n\ cdot 1 |n\ in\ mathbb {Z}\}\ end {ecuación*}

Esta observación no significa que cada entero sea el producto de un entero multiplicado por 1. Significa que

\ begin {ecuación*}\ mathbb {Z} =\ {0\}\ copa\ {\ overbrackets {1+1+\ cdots +1} ^ {n\ textrm {términos}}\ mid n\ in\ mathbb {P}\}\ copa\ {\ overcorsé {(-1) + (-1) +\ cdots + (-1)} ^ {n\ textrm {términos}\ medio n\ in\ mathbb {P}\}\ final {ecuación*}

Teorema$\PageIndex{1}$: Cyclic Implies Abelian

Si$[G;*]$ es cíclico, entonces es abeliano.

Prueba

Dejar$a$ ser cualquier generador de$G$ y dejar$b, c \in G\text{.}$ Por la definición del generador de un grupo, existen enteros$m$ y$n$ tal que$b = m a$ y$c = n a\text{.}$ Así, usando el Teorema 11.3.9,

\ begin {equation*}\ begin {split} b*c &= (m a) * (n a)\\ &= (m + n) a\\ &= (n + m) a\\ &= (n a) * (m a)\\ &= c*b\\ end {split}\ end {equation*}

Uno de los primeros pasos para probar una propiedad de los grupos cíclicos es utilizar el hecho de que existe un generador. Entonces cada elemento del grupo puede expresarse como algún múltiplo del generador. Toma nota especial de cómo se usa esto en los teoremas de esta sección.

Hasta ahora hemos utilizado únicamente notación aditiva para discutir grupos cíclicos. El teorema$\PageIndex{1}$ realmente justifica esta práctica ya que es costumbre usar notación aditiva cuando se discuten grupos abelianos. Por supuesto, algunos grupos concretos para los que empleamos notación multiplicativa son cíclicos. Si uno de sus elementos,$a\text{,}$ es un generador,

\ begin {ecuación*}\ langle a\ rangle =\ izquierda\ {a^n\ mid n\ in\ mathbb {Z}\ derecha\}\ final {ecuación*}

Ejemplo$\PageIndex{3}$: A Cyclic Multiplicative Group

El grupo de enteros positivos módulo 11 con multiplicación de módulo 11,$[\mathbb{Z}_{11}^* ;\times_{11}]\text{,}$ es cíclico. Uno de sus generadores es 6:$6^1 = 6\text{,}$$6^2 = 3\text{,}$$6^3= 7\text{,}$$\ldots$,$6^9=2\text{,}$ y$6^{10}=1\text{,}$ la identidad del grupo.

Ejemplo$\PageIndex{4}$: A Non-Cyclic Group

Los números reales con suma,$[\mathbb{R};+]$ es un grupo no cíclico. La prueba de esta afirmación requiere un poco más de generalidad ya que estamos diciendo que para todos$r \in \mathbb{R}\text{,}$$\langle r \rangle$ es un subconjunto propio de$\mathbb{R}\text{.}$ Si$r$ es distinto de cero, los múltiplos de$r$ se distribuyen sobre la línea real, como en la Figura$\PageIndex{2}$. Está claro entonces que hay muchos números reales, como$r/2\text{,}$ que no están en$\langle r \rangle\text{.}$

$clipboard_e8cc675a8ee91924fa0ab8ec3bc0145ae.png$ Figura$\PageIndex{2}$: Elementos de$\langle r \rangle, r>0$

Las dos pruebas siguientes hacen uso del Teorema 11.4.1.

El siguiente teorema muestra que un grupo cíclico nunca puede ser muy complicado.

Teorema$\PageIndex{2}$: Possible Cyclic Group Structures

Si$G$ es un grupo cíclico, entonces$G$ es finito o contablemente infinito. Si$G$ es finito y$\lvert G\rvert=n\text{,}$ es isomórfico a$[\mathbb{Z}_n; +_n]\text{.}$ Si$G$ es infinito, es isomórfico a$[\mathbb{Z};+]\text{.}$

Prueba

Caso 1:$\lvert G\rvert < \infty\text{.}$ Si$a$ es un generador de$G$ y$\lvert G\rvert =n\text{,}$ definir$\phi:\mathbb{Z}_n \to G$ por$\phi(k) = k a$ para todos$k \in \mathbb{Z}_n\text{.}$

Ya que$\langle a \rangle$ es finito, podemos usar el hecho de que los elementos de$\langle a \rangle$ son los primeros múltiplos$n$ no negativos de$a\text{.}$ A partir de esta observación, vemos que$\phi$ es una sobreyección. Una sobreyección entre conjuntos finitos de la misma cardinalidad debe ser una biyección. Por último, si$p,q \in \mathbb{Z}_n\text{,}$

\ begin {ecuación*}\ begin {split}\ phi (p) +\ phi (q) &= p a + q a\\ &= (p+q) a\\ &= (p +_n q) a\ quad\ textrm {ver ejercicio 15.1.10}\\ & =\ phi (p +_n q)\\ end {split}\ end {ecuación*}

Por lo tanto,$\phi$ es un isomorfismo.

Caso 2:$\lvert G\rvert =\infty\text{.}$ Dejaremos este caso como ejercicio.

Teorema$\PageIndex{3}$: Subgroups of Cyclic Groups

Cada subgrupo de un grupo cíclico es cíclico.

Prueba: Dejar$G$ ser cíclico con generador$a$ y dejar que$H \leq G\text{.}$ If$H = \{e\}\text{,}$$H$ tenga$e$ como generador. Ahora podemos suponer que$\lvert H\rvert \geq 2$ y$a \neq e\text{.}$ Let$m$ ser el número entero menos positivo tal que$m a$ pertenece a$H\text{.}$ Este es el paso clave. Nos deja poner en nuestras manos un generador de Ahora$H\text{.}$ vamos a mostrar que$c= m a$ genera$H\text{.}$ Ciertamente,$\langle c \rangle \subseteq H\text{,}$ pero supongamos que$\langle c \rangle \neq H\text{.}$ Entonces existe$b \in H$ tal que$b \notin \langle c \rangle\text{.}$ Ahora, ya que$b$ está$G\text{,}$ adentro existe$n \in \mathbb{Z}$ tal que$b = n a\text{.}$ Ahora aplicamos la propiedad de división y dividimos$n$ por$m\text{.}$$b = n a = (q m+r)a = (q m)a+r a\text{,}$ donde$0 \leq r < m\text{.}$ Observamos que$r$ no puede ser cero porque de lo contrario tendríamos$b = n a = q(m a) = q c \in \langle c \rangle\text{.}$ Por lo tanto,$r a = n a - (q m) a \in H\text{.}$ Esto contradice nuestra elección de$m$ porque$0 < r < m\text{.}$

Ejemplo$\PageIndex{5}$: All Subgroups of $\mathbb{Z}_{10}$

Los únicos subgrupos propios de$\mathbb{Z}_{10}$ son$H_1 = \{0, 5\}$ y$H_2 = \{0, 2, 4, 6, 8\}\text{.}$ Ambos son cíclicos:$H_1= \langle 5 \rangle\text{,}$ mientras que$H_2 = \langle 2 \rangle = \langle 4 \rangle = \langle 6 \rangle = \langle 8 \rangle\text{.}$ Los generadores de$\mathbb{Z}_{10}$ son 1, 3, 7 y 9.

Ejemplo$\PageIndex{6}$: All Subgroups of $\mathbb{Z}$

Con la excepción de$\{0\}\text{,}$ todos los subgrupos de$\mathbb{Z}$ son isomórficos a$\mathbb{Z}\text{.}$ Si$H \leq \mathbb{Z}\text{,}$ entonces$H$ es el subgrupo cíclico generado por el elemento menos positivo de$H\text{.}$ Es infinito y así por Teorema$\PageIndex{3}$ es isomórfico a$\mathbb{Z}\text{.}$

Citamos ahora un teorema útil para computar el orden de los subgrupos cíclicos de un grupo cíclico:

Teorema$\PageIndex{4}$: The Order of Elements of a Finite Cyclic Group

Si$G$ es un grupo cíclico de orden$n$ y$a$ es un generador$G\text{,}$ del orden de$k a$ es$n/d\text{,}$ donde$d$ está el mayor divisor común de$n$ y$k\text{.}$

Prueba: La prueba de este teorema se deja al lector.

Ejemplo$\PageIndex{7}$: Computation of an Order in a Cyclic Group

Para computar el orden de$\langle 18 \rangle$ en$\mathbb{Z}_{30}\text{,}$ observamos primero que 1 es un generador de$\mathbb{Z}_{30}$ y$18= 18(1)\text{.}$ El mayor divisor común de 18 y 30 es 6. De ahí que el orden de$\langle 18 \rangle$ sea 30/6, o 5.

En este punto, presentaremos la idea de un sumador rápido, una aplicación relativamente moderna (Winograd, 1965) de un teorema antiguo, el Teorema del resto chino. Presentaremos solo una visión general de la teoría y nos basaremos principalmente en ejemplos.

Por necesidad, la adición de enteros con una computadora es módulo de adición$n\text{,}$ para$n$ algún número mayor. Considera el caso donde$n$ es pequeño, como 64. Entonces la suma implica la adición de números binarios de seis dígitos. Considera el proceso de sumar 31 y 1. Supongamos que el sumador de la computadora toma como entrada dos cadenas de bits$a = \left\{a_0,a_1,a_2,a_3,a_4,a_5\right\}$$b=\left\{b_0,b_1,b_2,b_3,b_4,b_5\right\}$ y$a$ y genera$s = \left\{s_0,s_1,s_2,s_3,s_4,s_5\right\}\text{,}$ la suma de$a = 31 = (1, 1, 1, 1, 1, 0)$ y$b\text{.}$ Entonces, si y$b = 1 = (1, 0, 0, 0, 0, 0)\text{,}$$s$ será (0, 0, 0, 0, 0, 1), o 32. La salida$s_{ }=1$ no se puede determinar hasta que se hayan determinado todas las demás salidas. Si la adición se realiza con una máquina de estado finito, como en el Ejemplo 14.3.5, el tiempo requerido para obtener$s$ será de seis unidades de tiempo, donde una unidad de tiempo es el tiempo que se tarda en obtener una salida de la máquina. En general, el tiempo requerido para obtener$s$ será proporcional al número de bits. Teóricamente, este tiempo se puede disminuir, pero la explicación requeriría una larga digresión y nuestros resultados relativos no cambiarían tanto. Utilizaremos la regla de que el número de unidades de tiempo necesarias para realizar módulo de adición$n$ es proporcional a$\left\lceil \log_2n\right\rceil\text{.}$

Ahora vamos a introducir un problema hipotético que utilizaremos para ilustrar la idea de un sumador rápido. Supongamos que teníamos que sumar 1,000 números módulo$27720 = 8 \cdot 9 \cdot 5 \cdot 7\cdot 11\text{.}$ Por la regla anterior, ya que$2^{14} < 27720 < 2^{15}\text{,}$ cada adición tomaría 15 unidades de tiempo. Si la suma se inicializa a cero, se necesitarían 1,000 adiciones; así, se necesitarían 15 mil unidades de tiempo para hacer las adiciones. Podemos mejorar esta vez dramáticamente aplicando el Teorema del Resto Chino.

Teorema$\PageIndex{5}$: Chinese Remainder Theorem (CRT)

$n_1\text{,}$$n_2\text{,}$$\ldots\text{,}$$n_p$Sea enteros que no tengan un factor común mayor que uno entre cualquier par de ellos; es decir, son relativamente primos. Dejar$n = n_1n_2\cdots n_p\text{.}$ Definir

\ comenzar {ecuación*}\ thet a:\mathbb {Z} _n\ a\ mathbb {Z} _ {n_1}\ veces\ mathbb {Z} _ {n_2}\ veces\ cdots\ veces\ mathbb {Z} _ _ {n_p}\ fin {ecuación*}

por

\ begin {ecuación*}\ theta (k) =\ izquierda (k_1, k_2,\ ldots, k_p\ derecha)\ end {ecuación*}

donde para$1\leq i\leq p\text{,}$$0\leq k_i < n_i$ y$k\equiv k_i\left(\textrm{mod } n_i\right)\text{.}$ Entonces$\theta$ es un isomorfismo de$\mathbb{Z}_n$$\mathbb{Z}_{n_1}\times \mathbb{Z}_{n_2}\times \cdots \times \mathbb{Z}_{n_p}\text{.}$

El Teorema del Resto Chino se puede afirmar en varias formas diferentes, y su prueba se puede encontrar en muchos textos de álgebra abstracta.

Como vimos en el Capítulo 11,$\mathbb{Z}_6$ es isomórfico a$\mathbb{Z}_2 \times \mathbb{Z}_3$. Este es el caso más pequeño al que se puede aplicar el TRC. Un isomorfismo entre$\mathbb{Z}_6$ y$\mathbb{Z}_2 \times \mathbb{Z}_3$ es

\ begin {ecuación*}\ begin {array} {cc}\ theta (0) = (0,0) &\ theta (3) = (1,0)\\\ theta (1) = (1, 1) &\ theta (4) = (0, 1)\\ theta (2) = (0, 2) &\ theta (5) = (1,2)\\\ fin array}\ end {ecuación*}

Consideremos un caso algo más grande. Comenzamos seleccionando un módulo que pueda ser factorizado en un producto de números enteros relativamente primos:$n=21,600=2^5 3^3 5^2\text{.}$ En este caso los factores son$2^5=32\text{,}$$3^3=27\text{,}$ y no$5^2=25\text{.}$ necesitan ser potencias de primos, pero es fácil romper los factores en esta forma para asegurar números relativamente primos. Para agregar$\mathbb{Z}_n\text{,}$ necesitamos unidades de$\left\lceil \log _2n\right\rceil =15$ tiempo. Que$G=\mathbb{Z}_{32}\times \mathbb{Z}_{27}\times \mathbb{Z}_{25}\text{.}$ El CRT nos dé un isomorfismo entre$\mathbb{Z}_{21600}$ y$G\text{.}$ La idea básica detrás del sumador rápido, ilustrada en Figura$\PageIndex{3}$, es hacer uso de este isomorfismo. La notación x += a se interpreta como la instrucción para agregar el valor de a a a la variable x.

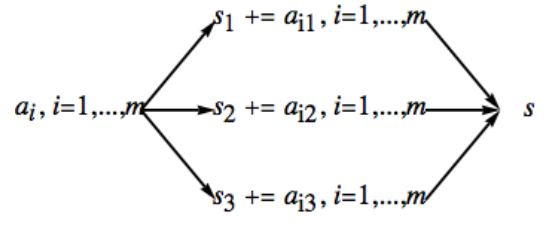$clipboard_e1ed5154c9c034939fac27b264b70829c.png$ Figura$\PageIndex{3}$: Esquema de sumador rápido

Supongamos que tenemos varios enteros$a_1, \ldots , a_m$ para agregar. Aquí, asumimos$m= 20\text{.}$ que calculamos la suma s para comparar nuestro resultado con esta verdadera suma.

a=[1878,1384,84,2021,784,1509,1740,1201,2363,1774,
   1865,33,1477,894,690,520,198,1349,1278,650]
s =0
for t in a:
    s+=t
s

Aunque nuestra suma es un cálculo entero, pondremos nuestro cálculo en el contexto de los enteros módulo 21600. El isomofismo desde$\mathbb{Z}_{21600}$ dentro$G=\mathbb{Z}_{32}\times \mathbb{Z}_{27}\times \mathbb{Z}_{25}$ se define en Sage como theta. Además demostramos que las operaciones en estos grupos son preservadas por theta.

G=cartesian_product([Integers(32),Integers(27),Integers(25)])
def theta(x):
    return G((x%32,x%27,x%25))
[theta(1878)+theta(1384),theta(1878+1384)]

Inicializamos las sumas en cada factor del rango de theta a cero y descomponemos cada suma$t$ en un triple$\theta(t)=\left(t_1,t_2,t_3\right)\in G\text{.}$

sum=G((0,0,0))
for t in a:
    sum+=theta(t)
sum

La suma en se$G$ puede hacer en paralelo de manera que cada nuevo subtotal en la forma del triple$(s_1,s_2, s_3)$ toma sólo el tiempo que se necesita para sumar en el módulo más grande, unidades de$\log _232=5$ tiempo, si los cálculos se hacen en paralelo. Por la regla de tiempo que hemos establecido, la suma de 20 números se puede hacer en unidades de$20\cdot 5= 100$ tiempo, a diferencia de unidades de$20\cdot 15 =300$ tiempo si hacemos los cálculos en$\mathbb{Z}_{21600}\text{.}$ Sin embargo el resultado es un triple en$G\text{.}$ La función que realiza la inversa de theta se construye en la mayoría programas de matemáticas, incluyendo Sage. En Sage la función es crt. Utilizamos esta función para calcular la inversa de nuestro triple, que es un elemento de$\mathbb{Z}_{21600}\text{.}$ El resultado no es la suma verdadera porque el módulo 21600 no es lo suficientemente grande. Sin embargo, verificamos que nuestro resultado es congruente con la suma verdadera módulo 21600.

isum=crt([12,13,17],[32,27,25])
[isum,(s-isum)%(21600)]

Para obtener la suma verdadera de nuestro esquema, habría que aumentar el módulo pasando de 21600 a, por ejemplo,$21600*23=496800\text{.}$ Mapeo en el nuevo grupo,$G=\mathbb{Z}_{32}\times \mathbb{Z}_{27}\times \mathbb{Z}_{25}\times \mathbb{Z}_{23}$ tardará un poco más, al igual que el proceso de inversión con crt, pero sumando las summands que están en forma de cuatriples se puede hacer sin tiempo adicional.

El cálculo de$\theta^{-1}\left(s_1,s_2,s_3\right)$ eso se realiza mediante la función Sage crt se puede lograr de diversas maneras. Todos ellos en última instancia se simplifican por el hecho de que también$\theta^{-1}$ es un isomorfismo. Un enfoque es utilizar la propiedad isomorfismo para darse cuenta de que el valor de$\theta^{-1}\left(s_1,s_2,s_3\right)$ es$s_1\theta^{-1}(1,0,0)+s_2\theta^{-1}(0,1,0)+s_3\theta^{-1}(0,0,1)\text{.}$ La aritmética en esta expresión está en el dominio de$\theta$ y consume más tiempo, pero solo necesita hacerse una vez. Es por ello que el sumador rápido sólo es práctico en situaciones en las que se deben realizar muchas adiciones para obtener una sola suma.

Las imágenes inversas de los “vectores unitarios” se pueden calcular antes de tiempo.

u=[crt([1,0,0],[32,27,25]),
   crt([0,1,0],[32,27,25]),crt([0,0,1],[32,27,25])]
u

El resultado que calculamos anteriormente puede ser calculado directamente por en el módulo mayor.

(7425*12 + 6400*13+ 7776* 17)%21600

Para ilustrar aún más el potencial de los sumadores rápidos, considere aumentar el módulo a$n=2^53^35^27^211\cdot 13\cdot 17\cdot 19\cdot 23\cdot 29\cdot 31\cdot 37\cdot 41\cdot 43\cdot 47\approx 3.1\times 10^{21}\text{.}$ Cada adición usando la$n$ adición de módulo habitual con sumadores completos tomaría 72 unidades de tiempo. Al descomponer cada suma en 15 tuplas según el CRT, el tiempo se reduce a unidades de$\left\lceil \log _249\right\rceil =6$ tiempo por adición.

Ejercicios

Ejercicio$\PageIndex{1}$

¿Qué generadores además de 1$[\mathbb{Z}; +]$ tiene?

Contestar: El único otro generador es$-1\text{.}$

Ejercicio$\PageIndex{2}$

Supongamos que$[G;*]$ es un grupo cíclico con generador$g\text{.}$ Si construyes una gráfica de con vértices a partir de los elementos de$G$ y edge set$E= \{(a, g*a) \mid a\in G\}\text{,}$ ¿cómo sería la gráfica? Si$G$ es un grupo de orden par, ¿cómo sería una gráfica con conjunto$E'= \{(a, g^2*a) \mid a\in G\}$ de bordes?

Ejercicio$\PageIndex{3}$

Demostrar que si$\lvert G \rvert >2$ y$G$ es cíclico,$G$ tiene al menos dos generadores.

Contestar

Si$\lvert G \rvert = m\text{,}$$m>2\text{,}$ y$G = \langle a \rangle\text{,}$ entonces$a\text{,}$$a^2,\ldots\text{,}$$a^{m-1}$,$a^m=e$ son elementos distintos de$G\text{.}$ Además,$a^{-1}= a^{m-1}\neq a\text{,}$ Si$1 \leq k \leq m\text{,}$$a^{-1}$ genera$a^k\text{:}$

\ begin {ecuation*}\ begin {split}\ left (a^ {-1}\ right) ^ {m-k} &=\ left (a^ {m-1}\ right) ^ {m-k}\\ & = a^ {m^2-m-m k + k}\\ & =\ izquierda (a^m\ derecha) ^ {m-k-1} *a^k\\ &= e*a^k=a^k\\\ final {dividir}\ final {ecuación*}

Del mismo modo, si$G$ es infinito y$G = \langle a\rangle\text{,}$ luego$a^{-1}$ genera$G\text{.}$

Ejercicio$\PageIndex{4}$

Si quisieras listar los generadores de$\mathbb{Z}_n$ ti solo tendrías que probar los primeros enteros$n/2$ positivos. ¿Por qué?

Ejercicio$\PageIndex{5}$

¿Cuáles de los siguientes grupos son cíclicos? Explique.

$\displaystyle [\mathbb{Q}; +]$
$\displaystyle [\mathbb{R}^+;\cdot ]$
$[6\mathbb{Z}; +]$donde$6\mathbb{Z} = \{6n |n \in \mathbb{Z}\}$
$\displaystyle \mathbb{Z} \times \mathbb{Z}$
$\displaystyle \mathbb{Z}_2\times \mathbb{Z}_3 \times \mathbb{Z}_{25}$

Contestar

No. Supongamos que$q \in \mathbb{Q}$ genera$\mathbb{Q}\text{.}$ Entonces$\langle q\rangle = \{n q : n \in \mathbb{Z}\}\text{.}$ Pero esto nos da a lo sumo múltiplos enteros de$q\text{,}$ no todos los elementos en$\mathbb{Q}\text{.}$
No. Razonamiento similar a la parte a.
Sí. 6 es un generador de$6\mathbb{Z}\text{.}$
No.
Sí,$(1,1, 1)$ es un generador del grupo.

Ejercicio$\PageIndex{6}$

Para cada grupo y elemento, determine el orden del subgrupo cíclico generado por el elemento:

$\mathbb{Z}_{25}$, 15
$\mathbb{Z}_4\times \mathbb{Z}_9$,$(2, 6)$ (aplicar Ejercicio$\PageIndex{8}$)
$\mathbb{Z}_{64}$, 2

Ejercicio$\PageIndex{7}$

¿Cómo$\PageIndex{4}$ se puede aplicar el Teorema para listar los generadores de$\mathbb{Z}_n\text{?}$ Cuáles son los generadores$\mathbb{Z}_{25}\text{?}$ de De$\mathbb{Z}_{256}\text{?}$

Contestar: Teorema$\PageIndex{4}$ implica que$a$ genera$\mathbb{Z}_n$ si y sólo si el mayor divisor común de$n$ y$a$ es 1. Por lo tanto, la lista de generadores de$\mathbb{Z}_n$ son los enteros en$\mathbb{Z}_n$ que son relativamente primos a$n\text{.}$ Los generadores de$\mathbb{Z}_{25}$ son todos los elementos distintos de cero excepto 5, 10, 15 y 20. Los generadores de$\mathbb{Z}_{256}$ son los enteros impares en$\mathbb{Z}_{256}$ ya que 256 es$2^8\text{.}$

Ejercicio$\PageIndex{8}$

Demostrar que si el mayor divisor común de$n$ y$m$ es 1, entonces (1, 1) es un generador de$\mathbb{Z}_n\times \mathbb{Z}_m\text{,}$ y por lo tanto,$\mathbb{Z}_n\times \mathbb{Z}_m$ es isomorfo a$\mathbb{Z}_{n m}\text{.}$

Ejercicio$\PageIndex{9}$

Ilustra cómo se puede usar el sumador rápido para agregar los números 21, 5, 7, y 15 usando el isomorfismo entre$\mathbb{Z}_{77}$ y$\mathbb{Z}_7\times \mathbb{Z}_{11}\text{.}$
Si se usa el mismo isomorfismo para sumar los números 25, 26 y 40, ¿cuál sería el resultado, por qué sería incorrecto y en qué se diferenciaría la respuesta de la respuesta en la parte a?

Contestar

$\theta :\mathbb{Z}_{77} \to \mathbb{Z}_7 \times \mathbb{Z}_{11}$mapea los enteros dados de la siguiente manera:
\ begin {ecuation*}\ begin {array} {ccc} 21 &\ to & (0,10)\\ 5 &\ to & (5,5)\\ 7 &\ to & (0,7)\\ 15 &\ to &\ subrayado {(1,4)}\\\ textrm {sum} =48 &\ leftarrow & (6,4) =\ textrm {suma}\\\ end {array}\ end { ecuación*}
La suma final, 48, se obtiene utilizando los hechos que$\theta ^{-1}(1,0) =22$ y$\theta ^{-1}(0,1)=56$
\ comienzan {ecuación*}\ comienzan {dividir}\ theta^ {-1} (6,4) = 6\ tiempos_ {77}\ theta ^ {-1} (1,0) + 4\ times_ {77}\ theta^ {-1} (0,1)\\ & =6\ times_ {77} 22 +_ {77} 4\ tiempos_ {77} 56\\ & =55 +_ {77} 70\\ & =48\\\ final {dividir}\ texto {.} \ end {ecuación*}
Usando el mismo isomorfismo:
\ begin {ecuation*}\ begin {array} {ccc} 25 &\ to & (4,3)\\ 26 &\ to & (5,4)\\ 40 &\ to & (5,7)\\ & &\ textrm {sum} =( 0,3)\\\ end {array}\ end {equation*}
\ begin {equation*}\ begin {split}\ theta ^ {-1} (0,3) &= 3\ horas_ {77}\ theta ^ {-1} (0,1)\\ & = 3\ horas_ {77} 56\\ & =14\\ final {dividir}\ texto {.} \ end {equation*}
La suma real es 91. Nuestro resultado es incorrecto, ya que 91 no está en$\mathbb{Z}_{77}\text{.}$ Aviso que 91 y 14 difieren en 77. Cualquier error que obtengamos usando esta técnica será un múltiplo de 77.

Ejercicio$\PageIndex{10}$

Demostrar que si$G$ es un grupo cíclico de orden$n$ con generador$a\text{,}$ y$p, q \in \{0, 1, \ldots , n - 1\}\text{,}$ luego$(p+q)a = \left(p+_nq\right)a\text{.}$