15.2: Cosets y Grupos de Factores

Considera el grupo\(\left[\mathbb{Z}_{12};+_{12}\right]\text{.}\) Como vimos en la sección anterior, podemos imaginar sus propiedades cíclicas con el arte de cuerdas de la Figura 15.1.1. Aquí nos interesarán los no generadores, como 3. Las líneas continuas de la Figura\(\PageIndex{1}\) muestran que solo se ha alcanzado un tercio de las tachuelas iniciando en cero y saltando a cada tercera tachuelas. Los números de estas tachuelas corresponden a\(\langle 3 \rangle = \{0, 3, 6, 9\}\text{.}\)

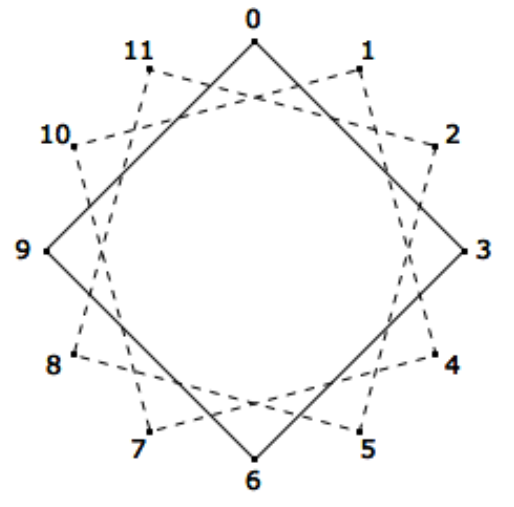Figura\(\PageIndex{1}\): Cosets “String art”

¿Qué pasa si comienzas en una de las tachuelas no utilizadas y vuelves a saltar a cada tres tachuelas? Los dos caminos rotos de la Figura\(\PageIndex{1}\) muestran que se producen cuadrados idénticos. Las tachuelas se dividen así en subconjuntos muy similares. Los subconjuntos a los\(\mathbb{Z}_{12}\) que corresponden son\(\{0, 3, 6, 9\}\text{,}\)\(\{1, 4, 7, 10\}\text{,}\) y\(\{2, 5, 8, 11\}\text{.}\) Estos subconjuntos se denominan coconjuntos. En particular, se les llama coconjuntos del subgrupo\(\{0, 3, 6, 9\}\text{.}\) Veremos que bajo ciertas condiciones, los coconjuntos de un subgrupo pueden formar un grupo propio. Antes de continuar con este ejemplo examinaremos la situación general.

Definición \(\PageIndex{1}\): Coset

Si\([G;*]\) es un grupo,\(H \leq G\) y\(a \in G\text{,}\) el coconjunto izquierdo de\(H\) generado por\(a\) es

\ comenzar {ecuación*} a*h =\ {a*h | h\ en H\}\ final {ecuación*}

y el coset correcto de\(H\) generado por\(a\) es

\ begin {ecuación*} h*a =\ {h*a | h\ in H\}. \ end {ecuación*}

Nota\(\PageIndex{1}\)

1. \(H\)en sí mismo es un coset izquierdo y derecho ya que\(e*H = H*e = H\text{.}\)
2. Si\(G\) es abeliano,\(a*H = H*a\) y se puede eliminar la distinción izquierda-derecha para los cosets. Normalmente usaremos notación coset izquierda en esa situación.

Definición\(\PageIndex{2}\): Cost Representative

Cualquier elemento de un coset se llama representante de ese coset.

Uno podría preguntarse si\(a\) es de alguna manera un representante especial de\(a*H\) ya que parece definir el coset. No lo es, como veremos.

Observación\(\PageIndex{1}\): A Duality Principle

Un principio de dualidad puede formularse con respecto a los cosets porque los cosets izquierdo y derecho se definen de manera similar. Cualquier teorema sobre los coconjuntos izquierdo y derecho dará lugar a un segundo teorema cuando “izquierda” y “derecha” se intercambien por “derecha” e “izquierda”.

Teorema\(\PageIndex{1}\)

Si\(b\in a*H\text{,}\) entonces\(a*H = b*H\text{,}\) y si\(b \in H*a\text{,}\) entonces\(H*a = H*b\text{.}\)

Prueba

A la luz de la observación anterior, sólo necesitamos probar la primera parte de este teorema. \(x \in a*H\text{.}\)Supongamos que solo necesitamos encontrar una manera de expresar\(x\) como “\(b\)veces un elemento de\(H\text{.}\)” Entonces habremos probado que\(a*H \subseteq b*H\text{.}\) Por la definición de\(a*H\text{,}\) desde\(b\) y\(x\) están\(a*H\text{,}\) ahí existen\(h_1\) y\(h_2\) en\(H\) tal eso\(b = a*h_1\) y\(x = a*h_2\text{.}\) Teniendo en cuenta estas dos ecuaciones,\(a = b h_1^{-1}\) y

\ start {ecuación*} x = a*h_2 = (b *h_1^ {-1}) *h_2 = b* (h_1^ {-1} *h_2)\ end {ecuación*}

Ya\(h_1,h_2 \in H\text{,}\)\(h_1^{-1}*h_2 \in H\text{,}\) y terminamos con esta parte de la prueba. Para demostrar que\(b*H \subseteq a*H\text{,}\) uno puede seguir esencialmente los mismos pasos, que dejaremos que el lector complete.

Ejemplo\(\PageIndex{1}\)

En Figura\(\PageIndex{1}\), se puede iniciar ya sea en 1 o 7 y obtener el mismo camino tomando saltos de tres tachuelas en cada paso. Así,

\ begin {ecuación*} 1+_ {12}\ {0, 3, 6, 9\} = 7 +_ {12}\ {0, 3, 6, 9\} =\ {1, 4, 7, 10\}. \ end {ecuación*}

El conjunto de coconjuntos izquierdo (o derecho) de un subgrupo particiona un grupo de una manera especial:

Teorema\(\PageIndex{2}\): Cosets Partition a Group

Si\([G; *]\) es un grupo y\(H\leq G\text{,}\) el conjunto de cosets izquierdos de\(H\) es una partición de\(G\text{.}\) Además, todos los coconjuntos izquierdos de\(H\) tienen la misma cardinalidad. Lo mismo es cierto para los cosets correctos.

Prueba

Que cada elemento de\(G\) pertenece a un coset de izquierda es claro porque\(a \in a*H\) para todos\(a \in G\text{.}\) Si\(a*H\) y\(b*H\) son cosets dejados, vamos a demostrar que son o iguales o disjuntos. Si\(a*H\) y no\(b*H\) son disjuntas, no\(a*H\cap b*H\) está vacío y algún elemento\(c \in G\) pertenece a la intersección. Entonces por teorema\(\PageIndex{1}\),\(c\in a*H \Rightarrow a*H = c*H\) y\(c \in b*H \Rightarrow b*H = c*H\text{.}\) por lo tanto\(a*H = b*H\text{.}\)

Completamos la prueba demostrando que cada coset izquierdo tiene la misma cardinalidad que\(H\text{.}\) Para ello, simplemente observamos que si\(a \in G\text{,}\)\(\rho:H \to a*H\) se define por\(\rho(h)= a*h\) es una biyección y de ahí\(\lvert H\rvert =\lvert a *H\rvert\text{.}\) dejaremos la prueba de esta afirmación al lector.

La función\(\rho\) tiene una interpretación agradable en términos de nuestro ejemplo de apertura. Si\(a \in \mathbb{Z}_{12}\text{,}\) la gráfica de\(\{0, 3, 6, 9\}\) se gira\((30a)^{\circ}\) para coincidir con uno de los tres coconjuntos de\(\{0, 3, 6, 9\}\text{.}\)

Corolario\(\PageIndex{1}\): A Coset Counting Formula

Si\(\lvert G\rvert < \infty\) y\(H\leq G\text{,}\) el número de cosets izquierdos distintos de\(H\) iguales\(\frac{\lvert G\rvert }{\lvert H\rvert }\text{.}\) Por esta razón usamos\(G/H\) para denotar el conjunto de cosets izquierdos de\(H\) in\(G\)

Prueba

Esto se deduce de la partición\(G\) en conjuntos de igual tamaño, uno de los cuales es\(H\text{.}\)

Ejemplo\(\PageIndex{2}\)

El conjunto de múltiplos enteros de cuatro,\(4\mathbb{Z}\text{,}\) es un subgrupo de\([\mathbb{Z}; +]\text{.}\) Cuatro coconjuntos distintos de\(4\mathbb{Z}\) partición los enteros. Están\(4\mathbb{Z}\text{,}\)\(1+4\mathbb{Z}\text{,}\)\(2+4\mathbb{Z}\text{,}\) y\(3+4\mathbb{Z}\text{,}\) donde, por ejemplo, también se\(1+4\mathbb{Z} = \{1+4k | k \in \mathbb{Z}\}\text{.}\)\(4\mathbb{Z}\) pueden escribir\(0+4\mathbb{Z}\text{.}\)

Convención\(\PageIndex{1}\): Distinguished Representatives

Aunque hemos visto que cualquier representante puede describir un coset, a menudo es conveniente seleccionar un representante distinguido de cada coset. La ventaja de hacer esto es que hay un nombre único para cada coset en términos de su distinguido representante. En ejemplos numéricos como el anterior, el representante distinguido suele ser el representante no negativo más pequeño. Recuerde, esto es puramente una conveniencia y no hay absolutamente nada malo en la escritura\(-203+4\mathbb{Z}\text{,}\)\(5+4\mathbb{Z}\text{,}\) o\(621+4\mathbb{Z}\) en lugar de\(1+4\mathbb{Z}\) porque\(-203, 5, 621 \in 1+4\mathbb{Z}\text{.}\)

Antes de completar el empuje principal de esta sección, tomaremos nota de una implicación significativa del Teorema\(\PageIndex{2}\). Dado que un grupo finito se divide en coconjuntos de un tamaño común por cualquier subgrupo, podemos concluir:

Teorema\(\PageIndex{3}\): Lagrange's Theorem

El orden de un subgrupo de un grupo finito debe dividir el orden del grupo.

Una implicación inmediata del Teorema de Lagrange es que si\(p\) es primo, no\(\mathbb{Z}_p\) tiene subgrupos propios.

A continuación describiremos la operación sobre cosets que, bajo ciertas circunstancias, resultará en un grupo. Para la mayor parte de esta sección, asumiremos que\(G\) es un grupo abeliano. Esta es una condición suficiente (pero no necesaria) que garantiza que el conjunto de cosets izquierdos formará un grupo.

Definición\(\PageIndex{3}\): Operation on Cosets

Dejar\(C\) y\(D\) quedar coconjuntos de\(H\text{,}\) un subgrupo de\(G\) con representantes\(c\) y\(d\text{,}\) respectivamente. Entonces

\ comenzar {ecuación*} C\ oveces D = (C*h)\ oveces (D*h) = (c*d) *H\ final {ecuación*}

La operación\(\otimes\) se llama la operación inducida en los cosets izquierdos por\(*\text{.}\)

En Teorema\(\PageIndex{4}\), más adelante en esta sección, vamos a demostrar que si\(G\) es un grupo abeliano,\(\otimes\) es efectivamente una operación. En la práctica, si el grupo\(G\) es un grupo aditivo, el símbolo\(\otimes\) se sustituye por\(+\text{,}\) como en el siguiente ejemplo.

Ejemplo\(\PageIndex{3}\): Computing with Cosets of \(4\mathbb{Z}\)

Considera los cosets descritos en Ejemplo\(\PageIndex{2}\). Por brevedad, renombramos\(0+4\mathbb{Z}\text{,}\)\(1+4\mathbb{Z}\text{,}\)\(2+4\mathbb{Z}\text{,}\)\(\bar{0}\text{,}\)\(\bar{1}\text{,}\)\(\bar{2}\text{,}\) y\(3+4\mathbb{Z}\) con los símbolos y\(\bar{3}\text{.}\) hagamos un cálculo típico,\(\bar{1}+\bar{3}\text{.}\) veremos que el resultado siempre va a ser\(\bar{0}\), no importa qué representantes seleccionemos. Por ejemplo,\(9 \in \bar{1}\text{,}\)\(7\in \bar{3}\text{,}\) y\(9+7=16 \in \bar{0}\text{.}\) Nuestra elección de los representantes\(\bar{1}\) y\(\bar{3}\) fueron completamente arbitrarios.

En general, se\(C \otimes D\) puede computar de muchas maneras, por lo que es necesario demostrar que la elección de los representantes no afecta el resultado. Cuando el resultado que obtenemos para siempre\(C \otimes D\) es independiente de nuestra elección de representantes, decimos que “\(\otimes\)está bien definido”. La adición de coconjuntos es una operación bien definida en los coconjuntos izquierdos de 4\(\mathbb{Z}\) y se resume en la siguiente tabla. ¿Te das cuenta de algo familiar?

\ begin {ecuation*}\ begin {array} {c|cccc}\ otimes &\ bar {0} &\ bar {1} &\ bar {2} &\ bar {3}\\ hline\ bar {0} &\ bar {0} &\ bar {1} &\ bar {2} &\ bar {3}\\ bar {1} &\ bar {1} &\ bar {1} &\ bar {2} &\ bar {3} &\ bar {0}\\ bar {2} &\ bar {2} &\ bar {3} &\ bar {0} &\ bar {1}\\ bar {3} &\ bar {3} &\ bar {0} &\ bar {1} &\ bar {2}\\ final {array}\ final {ecuación*}

Ejemplo\(\PageIndex{4}\): Cosets of the Integers in the Group of Real Numbers

Consideremos el grupo de números reales,\([\mathbb{R}; +]\text{,}\) y su subgrupo de enteros,\(\mathbb{Z}\text{.}\) Cada elemento de\(\mathbb{R}/\mathbb{Z}\) tiene la misma cardinalidad\(\mathbb{Z}\text{.}\) que Let\(s, t\in \mathbb{R}\text{.}\)\(s\in t+\mathbb{Z}\) if se\(s\) puede escribir\(t+n\) para algunos\(n \in \mathbb{Z}\text{.}\) Por lo tanto\(s\) y\(t\) pertenecer al mismo coconjunto si difieren por un entero. (Ver Ejercicio\(\PageIndex{6}\) para una generalización de este hecho.)

Ahora considere el coset Los números\(0.25+\mathbb{Z}\text{.}\) reales que difieren en un entero de 0.25 son\(1.25, 2.25, 3.25, \ldots\) y\(-0.75, -1.75, -2.75, \ldots\text{.}\) si se selecciona algún número real, existe un representante de su coset que sea mayor o igual a 0 y menor que 1. Llamaremos a ese representante el distinguido representante del coset. Por ejemplo, 43.125 pertenece al coset representado por 0.125;\(-6.382+\mathbb{Z}\) tiene 0.618 como su representante distinguido. La operación en comúnmente\(\mathbb{R}/\mathbb{Z}\) se llama módulo de adición 1. Algunos cálculos típicos en\(\mathbb{R}/\mathbb{Z}\) son

\ begin {ecuación*}\ begin {array} {c} (0.1+\ mathbb {Z}) + (0.48+\ mathbb {Z}) = 0.58+\ mathbb {Z}\\ (0.7+\ mathbb {Z}) + (0.31+\ mathbb {Z}) = 0.01+\ mathbb {Z}\ - (0.41+\ mathbb {Z}) = -0.41+\ mathbb {Z} = 0.59+\ mathbb {Z}\\ textrm {y en general,} - (a+\ mathbb {Z}) = (1 - a) +\ mathbb {Z}\ end {array}\ text {.} \ end {ecuación*}

Ejemplo\(\PageIndex{5}\): Cosets in a Direct Product

Considere\(F = (\mathbb{Z}_4\times \mathbb{Z}_2 )/H\text{,}\) dónde\(H=\{(0,0),(0,1)\}\text{.}\)\(\mathbb{Z}_4 \times \mathbb{Z}_2\) Since es de orden 8, cada elemento de\(F\) es un coset que contiene dos pares ordenados. Le dejaremos al lector verificar que los cuatro coconjuntos distintos son\((0, 0)+H\text{,}\)\((1,0) +H\text{,}\)\((2, 0)+H\) y\((3, 0)+H\text{.}\) El lector también puede verificar que\(F\) es isomórfico a\(\mathbb{Z}_4\), ya que\(F\) es cíclico. Una conjetura educada debería darte un generador.

Ejemplo\(\PageIndex{6}\)

Considera al grupo\(\mathbb{Z}_2{}^4 = \mathbb{Z}_2\times \mathbb{Z}_2\times \mathbb{Z}_2\times \mathbb{Z}_2\). Dejar\(H\) ser\(\langle (1,0,1, 0)\rangle\text{,}\) el subgrupo cíclico de\(\mathbb{Z}_2{}^4\) generar por (1,0,1,0). Desde

\ begin {ecuación*} (1,0,1, 0) + (1,0,1, 0) = (1+_21,0+_20,1+_21,0+_20) = (0,0,0,0)\ end {ecuación*}

el orden de\(H\) es 2 y,\(\mathbb{Z}_2{}^4/H\) tiene\(\lvert \mathbb{Z}_2^4 /H\rvert =\frac{\lvert \mathbb{Z}_2^4\rvert }{\lvert H\rvert }=\frac{16}{2}= 8\) elementos. Un coset típico es

\ start {ecuación*} C = (0, 1, 1, 1) +H =\ {(0, 1, 1, 1, 1), (1, 1, 0, 1)\}\ final {ecuación*}

Obsérvese que dado que\(2(0, 1, 1, 1) = (0, 0, 0, 0)\text{,}\)\(2C = C\otimes C = H\text{,}\) la identidad para\(\mathbb{Z}_2{}^4/H\text{.}\) la operación en Los órdenes de elementos no identitarios de este grupo de factores son todos 2, y se puede demostrar que el grupo factorial es isomórfico a\(\mathbb{Z}_2{}^3\text{.}\)

Teorema \(\PageIndex{4}\): Coset Operation is Well-Defined (Abelian Case)

Si\(G\) es un grupo abeliano, y\(H \leq G\text{,}\) la operación inducida en cosets de\(H\) por la operación de\(G\) está bien definida.

Prueba

Supongamos que\(a\text{,}\)\(b\text{,}\) y\(a'\text{,}\)\(b'\text{.}\) son dos opciones para los representantes de los cosets\(C\) y\(D\text{.}\) Es decir que\(a, a' \in C\text{,}\)\(b, b' \in D\text{.}\) vamos a demostrar eso\(a*b\) y\(a'*b'\) somos representantes del mismo coset. Teorema\(\PageIndex{1}\) implica que\(C = a*H\) y\(D = b*H\text{,}\) así tenemos\(a' \in a*H\) y\(b' \in b*H\text{.}\) Entonces existe\(h_1, h_2 \in H\) tal que\(a' = a*h_1\) y\(b' = b*h_2\) y así

\ start {ecuación*} a'*b' = (a*h_1) * (b*h_2) = (a*b) * (h_1*h_2)\ end {ecuación*}

por diversas propiedades grupales y la suposición que\(G\) es abeliana, lo que nos permite revertir el orden en que\(b\) y\(h_1\) aparecer en la cadena de igualdades. Esta última expresión para\(a'*b'\) implica que\(a'*b' \in (a*b)*H\) ya que\(h_1*h_2 \in H\) porque\(H\) es un subgrupo de\(G\text{.}\) Así, obtenemos el mismo coset para ambas parejas de representantes.

Teorema\(\PageIndex{5}\)

Dejar\(G\) ser un grupo y\(H \leq G\text{.}\) Si la operación inducida en los cosets izquierdos de\(H\) por la operación de\(G\) está bien definida, entonces el conjunto de cosets izquierdos forma un grupo bajo esa operación.

Prueba

Dejemos\(C_1\)\(,C_2\text{,}\) y\(C_3\) sean los cosets de izquierda con representantes\(r_1\text{,}\)\(r_2\text{,}\) y\(r_3\text{,}\) respectivamente. Los valores de\(C_1 \otimes \left(C_2 \otimes C_3\right)\) y\(\left(C_1\ \otimes C_2\right)\otimes C_3\) están determinados por\(r_1 * \left(r_2 * r_3\right)\) y\(\left(r_1 * r_2\right) * r_3\text{,}\) respectivamente. Por la asociatividad de\(*\) en\(G\text{,}\) estos dos elementos de grupo son iguales y así las dos expresiones coset deben ser iguales. Por lo tanto, la operación inducida es asociativa. En cuanto a la identidad y las propiedades inversas, no hay sorpresa. El coconjunto de identidad es\(H\text{,}\) o\(e*H\text{,}\) el coconjunto que contiene\(G\) la identidad de. Si\(C\) es un coset con representante es\(a\text{;}\) decir, si\(C = a*H\text{,}\) entonces\(C^{-1}\) es\(a^{-1}*H\text{.}\)

\ begin {ecuación*} (A*h)\ oveces\ izquierda (a^ {-1} *H\ derecha) =\ izquierda (a*a^ {-1}\ derecha) *H = E*h =\ textrm {identidad}\ textrm {coset}\ texto {.} \ end {ecuación*}

Definición \(\PageIndex{4}\): Factor Group

Dejar\(G\) ser un grupo y\(H \leq G\text{.}\) si el conjunto de cosets izquierdos de\(H\) forma un grupo, entonces ese grupo se llama el grupo factor de “\(G\)modulo\(H\text{.}\)” Se denota\(G/H\text{.}\)

Nota\(\PageIndex{2}\)

Si\(G\) es abeliano, entonces cada subgrupo de\(G\) produce un grupo de factores. Retrasaremos la consideración del caso no abeliano a la Sección 15.4.

Observación\(\PageIndex{2}\): On Notation

Se acostumbra usar el mismo símbolo para la operación de\(G/H\) como para la operación en\(G\text{.}\) La razón por la que usamos símbolos distintos en esta sección fue para hacer clara la distinción entre las dos operaciones.

Ejercicios

Ejercicio\(\PageIndex{1}\)

Considerar\(\mathbb{Z}_{10}\) y los subconjuntos de\(\mathbb{Z}_{10}\text{,}\)\(\{0, 1, 2, 3, 4\}\) y\(\{5, 6, 7, 8, 9\}\text{.}\) ¿Por qué la operación inducida en estos subconjuntos por la adición del módulo 10 no está bien definida?

Responder

Un ejemplo de una respuesta correcta válida: Llamar a los subconjuntos\(A\) y\(B\) respectivamente. Si elegimos\(0 \in A\) y\(5 \in B\) obtenemos\(0 +_{10} 5 =5 \in B\text{.}\) Por otro lado, si elegimos\(3 \in A\) y\(8 \in B\text{,}\) obtenemos\(3 +_{10} 8 = 1 \in A\text{.}\) Por lo tanto, la operación inducida no está bien definida en\(\{A,B\}\text{.}\)

Ejercicio\(\PageIndex{2}\)

¿Se te ocurre un grupo\(G\text{,}\) con un subgrupo\(H\) tal que\(\lvert H\rvert = 6\) y\(\lvert G/H\rvert = 6\text{?}\) es tu respuesta única?

Ejercicio\(\PageIndex{3}\)

Para cada grupo y subgrupo, ¿a qué es\(G/H\) isomórfico?

1. \(G = \mathbb{Z}_4 \times \mathbb{Z}_2\)y\(H = \langle (2, 0)\rangle\text{.}\) Comparar con Ejemplo\(\PageIndex{5}\).
2. \(G = [\mathbb{C}; +]\)y\(H = \mathbb{R}\text{.}\)
3. \(G\)=\(\mathbb{Z}_{20}\) y\(H = \langle 8\rangle\text{.}\)

Responder

1. Los cuatro coconjuntos distintos en\(G/H\) son\(H = \{(0, 0), (2, 0)\}\text{,}\)\((1, 0) + H= \{(1,0),(3,0)\}\text{,}\)\((0, 1) + H= \{(0,1),(2,1)\}\text{,}\) y\((1, 1) + H= \{(1,1),(3,1)\}\text{.}\) Ninguno de estos coconjuntos genera,\(G/H\text{;}\) por lo tanto, no\(G/H\) es cíclico. Por lo tanto,\(G/H\) debe ser isomórfico para\(\mathbb{Z}_2\times \mathbb{Z}_2\text{.}\)
2. El grupo de factores es isomórfico a\([\mathbb{R}; +]\text{.}\) Cada coconjunto de\(\mathbb{R}\) es una línea en el plano complejo que es paralela al eje x:\(\tau :\mathbb{C}/\mathbb{R}\to \mathbb{R}\text{,}\) donde\(T(\{a + b i\mid a\in \mathbb{R}\}) = b\) es un isomorfismo.
3. \(\langle 8\rangle = \{0, 4, 8, 12, 16\} \)\(\Rightarrow\)\(\lvert \mathbb{Z}_{20}/\langle 8\rangle \rvert =4\text{.}\)Los cuatro coconjuntos son:\(\bar{0}\text{,}\)\(\bar{1}\text{,}\)\(\bar{2}\text{,}\) y\(\bar{3}\text{.}\) 1 genera los cuatro coconjuntos. El grupo de factores es isomórfico\([\mathbb{Z}_4; +_4]\) porque\(\bar{1}\) es un generador.

Ejercicio\(\PageIndex{4}\)

Para cada grupo y subgrupo, ¿a qué es\(G/H\) isomórfico?

1. \(G = \mathbb{Z}\times \mathbb{Z}\)y\(H = \{(a, a) | a \in \mathbb{Z}\}\text{.}\)
2. \(G = \left[\mathbb{R}^*; \cdot \right]\)y\(H = \{1, -1\}\text{.}\)
3. \(G =\mathbb{Z}_2{}^5\)y\(H = \langle (1, 1, 1, 1, 1)\rangle\text{.}\)

Ejercicio\(\PageIndex{5}\)

Supongamos que\(G\) es un grupo,\(H \leq G\text{,}\) y\(a, b \in G\text{.}\) Probar que\(a*H= b*H\) si y solo si\(b^{-1}*a \in H\text{.}\)

Responder

\ begin {ecuación*}\ begin {split} a*h= b*h &\ Leftrightarrow a\ in b H\\ &\ Leftrightarrow a = b * h\ textrm {para algunos} h\ in H\ &\ Izquierda b^ {-1} *a = h\ textrm {para algunos} h\ en H\ &\ Izquierda tarrow b^ {-1} *a\ en H\\\ end {split}\ end {ecuación*}

Ejercicio\(\PageIndex{6}\)

1. El módulo de adición real\(r\text{,}\)\(r > 0\text{,}\) puede describirse como la operación inducida en cosets de\(\langle r\rangle\) por adición ordinaria. Describir un sistema de representantes distinguidos para los elementos de\(\mathbb{R}/\langle r\rangle\text{.}\)
2. Considera la función trigonométrica seno. Dado que\(\sin (x+2\pi k) = \sin x\) para todos\(x\in \mathbb{R}\) y\(k\in \mathbb{Z}\text{,}\) mostrar cómo los distinguidos representantes de\(\mathbb{R}/\langle 2\pi \rangle\) pueden ser útiles en el desarrollo de un algoritmo para calcular el seno de un número.

Ejercicio\(\PageIndex{7}\)

Completar la prueba del Teorema\(\PageIndex{2}\) demostrando que si\(a \in G\text{,}\)\(\rho:H \to a*H\) se define por\(\rho(h)= a*h\) es una biyección.