8.1: Conceptos básicos y ejemplos
- Page ID
- 117973
Cualquier sistema matemático debe tener un punto de partida; no podemos crear algo de la nada. El punto de partida de un sistema matemático (o de cualquier sistema lógico, para el caso) es una colección de terminología básica acompañada de una colección de hechos asumidos sobre las cosas que describe la terminología.
una etiqueta para un objeto o acción que se deja indefinido
una declaración (generalmente involucrando términos primitivos o términos definidos en términos de términos primitivos) que se considera verdadera sin pruebas
una colección de términos primitivos y axiomas
Términos Primitivos
- woozle (sustantivo),
- dorple (sustantivo),
- snarf (verbo).
Axiomas
- Existen al menos tres woozles distintos.
- Un woozle engancha un dorple si y solo si el dorple engancha al woozle.
- Cada par de distintos woozles engaña exactamente una dorpla en común.
- Hay por lo menos un trío de distintos woozles que no roncan ninguna dorpla en común.
- Cada dorpla es engrosada por al menos dos woozles distintos.
En el sistema axiomático del Axioma\(\PageIndex{1}\), el Axioma 1 es redundante, ya que podemos inferir de Axioma 4 que existen tres woozles distintos. Pero no hay daño en incluir este axioma para mayor claridad. Además, posteriormente investigaremos el efecto de alterarlo.
El sistema axiomático del Ejemplo\(\PageIndex{1}\) parece una tontería, pero en realidad podemos probar las cosas a partir de él.
Existen al menos tres dorplas distintas.
- Prueba
-
(En esta prueba, todas las referencias a axiomas se refieren a los axiomas de\(\PageIndex{1}\).)
Por Axioma 4, existe un trío\(w_1,w_2,w_3\) de distintos woozles que no roncan ninguna dorpla en común. Rompiendo este trío en varios pares y aplicando Axioma 3, vemos que existe una dorpla\(d_1\) que\(w_1\) y\(w_2\) ambos gruñen en común, también existe una dorpla\(d_2\) que\(w_1\) y\(w_3\) ambos gruñidos en común, y también existe una dorpla\(d_3\) que\(w_2\) y\(w_3\) ambos snarf en común. Estas relaciones snarfing se ilustran en el siguiente diagrama.
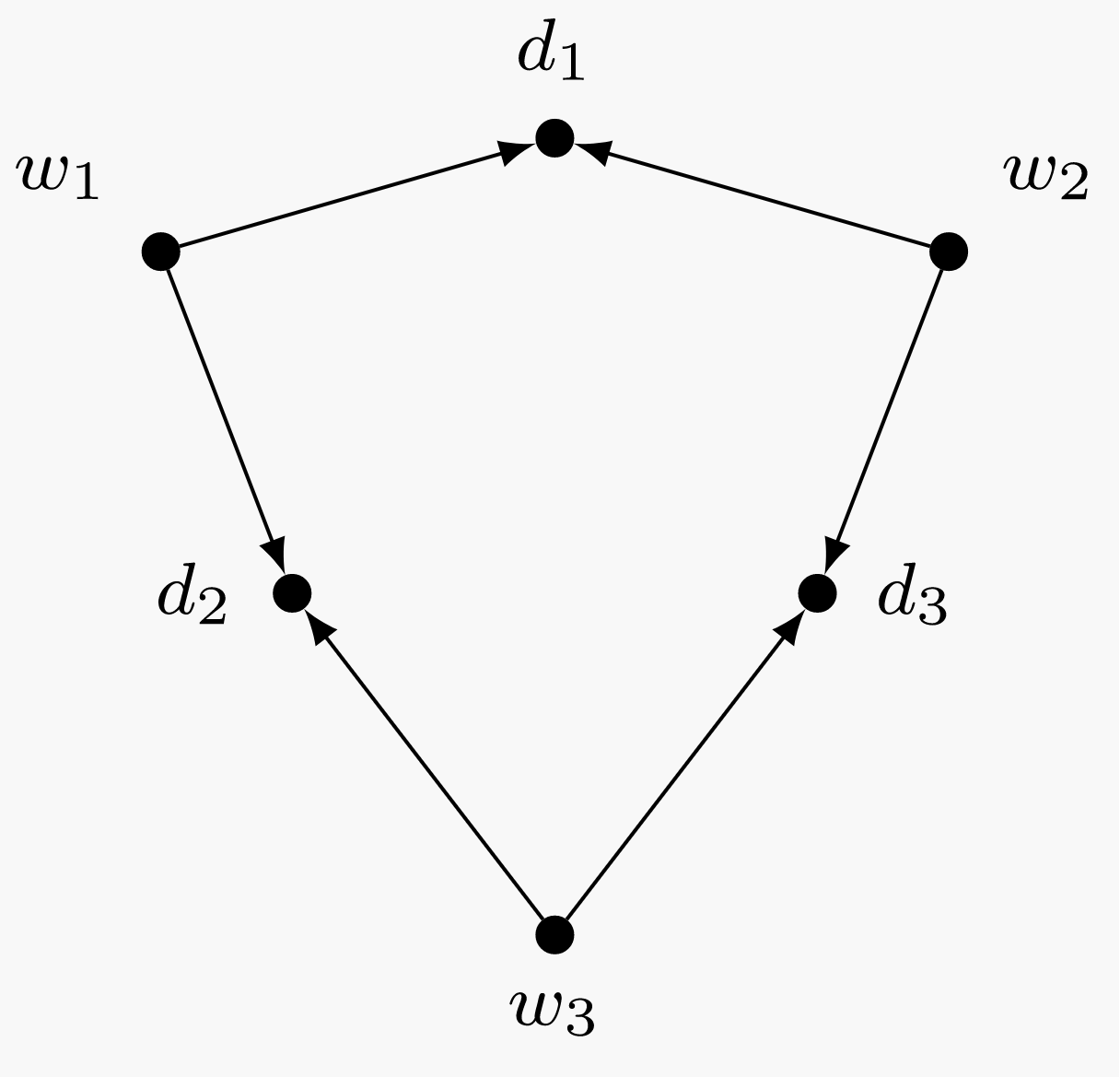
Figura\(\PageIndex{1}\): Diagrama de dorples engrosantes de woozles. Ahora, supongamos\(d_1\) y en realidad\(d_2\) eran el mismo dorple —entonces los tres woozles lo gruñirían en común.
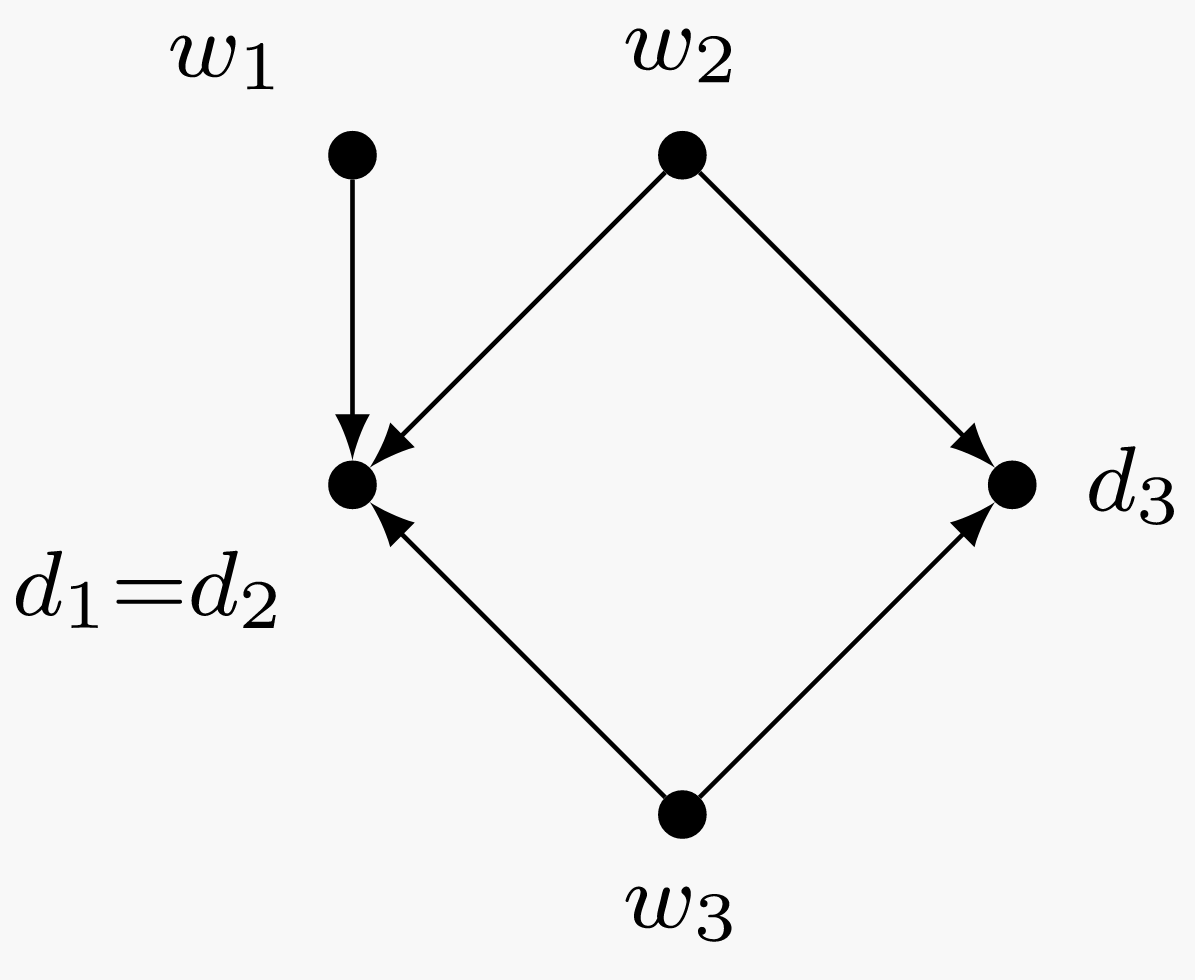
Figura\(\PageIndex{2}\): Diagrama de los dorples engrosantes de woozles, asumiendo que dos de los dorples coinciden. Como esto contradice nuestra suposición inicial, debe darse el caso que\(d_1\) y\(d_2\) son distintos. Argumentos similares nos permiten concluir también que\(d_1 \ne d_3\) y\(d_2 \ne d_3\text{.}\)
A menudo es útil dar nombres a propiedades importantes de los objetos.
una etiqueta para un objeto o acción que se define en términos de términos primitivos, axiomas y/u otros términos definidos
una explicación formal del significado de un término definido
Aquí hay una definición relativa al sistema axiomático de Ejemplo\(\PageIndex{1}\).
Solución
Snarf Buddies
dos dorplas distintas que arrebatan un woozle común
Una definición nos permite comunicar de manera más sucinta ideas y hechos sobre los objetos de un sistema axiomático.
Un par de amigos snarf snarf snarf un woozle único en común.
- Prueba
-
Supongamos que\(d_1,d_2\) son amigos snarf. Por contradicción, supongamos que gruñen más de un woozle en común:\(w_1,w_2\) seamos distintos woozles ambos gruñidos\(d_2\text{.}\) por\(d_1\) y Por Axioma 2, cada uno de\(w_1,w_2\) gruñidos cada uno de\(d_1,d_2\text{.}\) Pero esto contradice al Axioma 3, ya que dos woozles distintos no pueden gruñir más de un dorple en común.
Supongamos que reemplazamos el Axioma 1 en el sistema de Ejemplo por\(\PageIndex{1}\) lo siguiente.
- Existen exactamente tres woozles distintos.
En el nuevo sistema axiomático modificado, nuestros dos teoremas anteriores (Teorema\(\PageIndex{1}\) y Teorema\(\PageIndex{2}\)) siguen siendo ciertos, porque sigue siendo cierto que existen al menos tres woozles distintos. Pero ahora también podemos probar lo siguiente.
En el sistema axiomático de Ejemplo\(\PageIndex{1}\) con la versión modificada anterior del Axioma 1, existen exactamente tres dorplas distintas.
- Prueba
-
Se le pide que lo demuestre en los ejercicios.
Un sistema sin sentido como el de Ejemplo\(\PageIndex{1}\) es justamente eso —tonterías— y de poco uso a menos que haya ejemplos reales a los que se pueda aplicar la teoría desarrollada.
un sistema obtenido sustituyendo los términos primitivos en un sistema axiomático por términos más “concretos” de tal manera que todos los axiomas son verdaderas afirmaciones sobre los nuevos términos
Si estamos de acuerdo en que las afirmaciones del axioma siguen siendo todas ciertas con los nuevos términos, entonces cualquier teorema probado bajo el sistema abstracto sigue siendo válido en el nuevo sistema modelo.
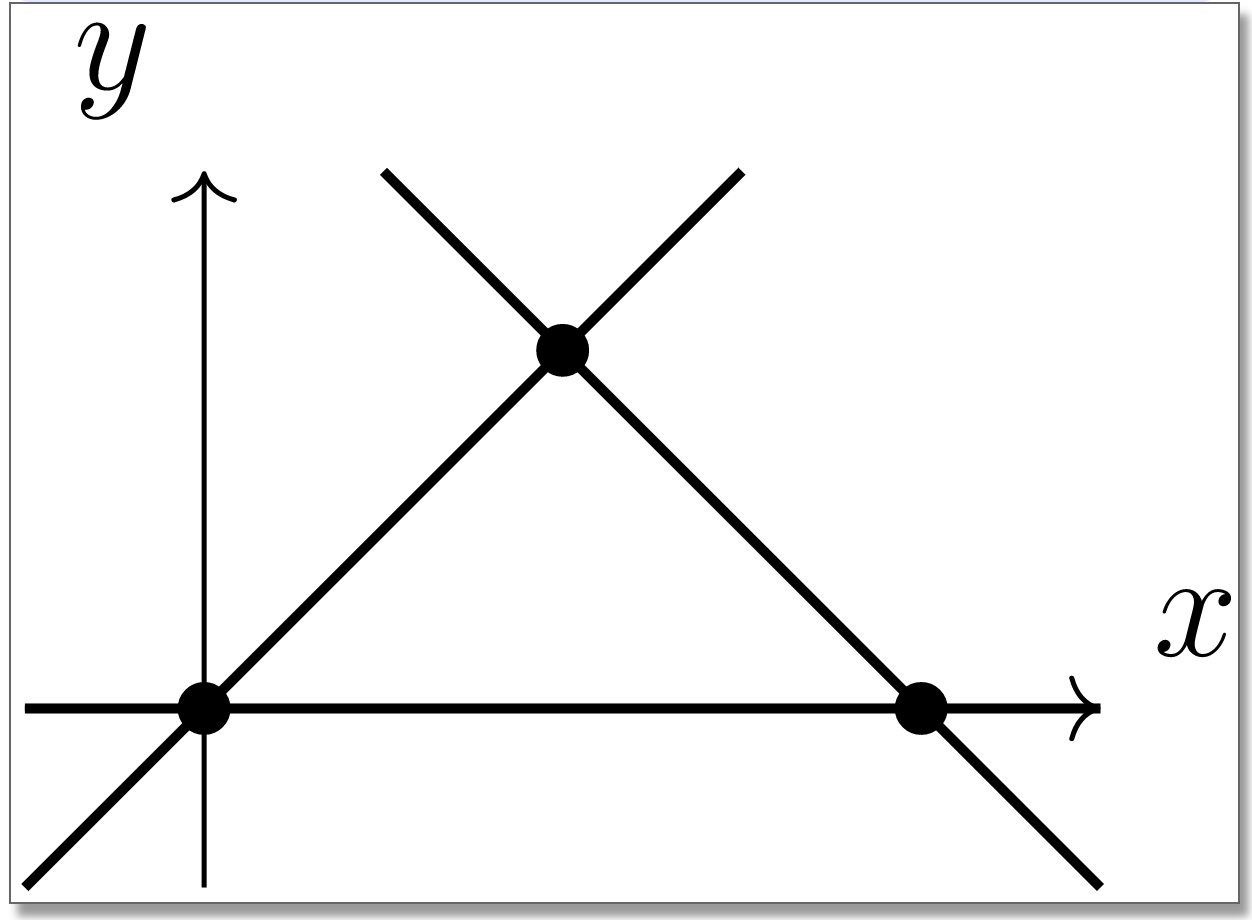
De nuevo consideremos el sistema axiomático de Ejemplo\(\PageIndex{1}\), aún utilizando la versión modificada de Axioma 1. Que los tres woozles distintos sean los puntos\((0,0)\text{,}\)\((1,1)\text{,}\) y\((2,0)\) en el plano cartesiano. Dejemos dorple ahora línea media en el plano, y vamos gruñir ahora significa mentiras en. Convénzase de que los axiomas del sistema son todos ciertos con esta interpretación de los términos primitivos.
El teorema\(\PageIndex{3}\) ahora dice que existen exactamente tres líneas distintas en el plano que encajan en nuestro sistema axiomático; ¿puedes encontrar sus ecuaciones?
Usar términos sin sentido como woozle, dorple y snarf para los términos primitivos en un sistema axiomático no suele ser una buena idea, ya que quita toda la intuición del proceso de descubrimiento de afirmaciones que se pueden deducir de los axiomas. Hubiera sido mucho mejor si hubiéramos usado las palabras punto en lugar de woozle, línea en lugar de dorple, y mienten en lugar de gruñidos como nuestros términos primitivos, para poder usar nuestra intuición sobre cómo interactúan tales objetos. En tal caso, los axiomas que elegimos deben ser un reflejo de nuestra idea de las propiedades más simples posibles sobre los términos primitivos, propiedades que todos razonablemente podrían estar de acuerdo son “verdaderas” sin pruebas. Sin embargo, para que los teoremas deducidos de tal sistema axiomático tengan la aplicabilidad más amplia posible, debemos dejar las palabras punto y línea como términos verdaderamente primitivos, indefinidos, es decir, punto y línea no deben considerarse como significantes punto en el plano y línea en el plano, como en el ejemplo anterior, sino más bien simplemente dejado como alguna idea abstracta, intuitiva de punto y línea.


