13.1: Conceptos básicos y ejemplos
- Page ID
- 118046
Si\(A\) es un conjunto que tiene el mismo tamaño que\(\mathbb{N}\text{,}\) entonces podemos pensar en una bijección\(\mathbb{N} \to A\) como “contar” los elementos de\(A\) (aunque haya un número infinito de elementos para contar), exactamente de la misma manera que usamos nuestros conjuntos de conteo\(\mathbb{N}_{<m}\) para contar conjuntos finitos.
un conjunto que es finito o tiene el mismo tamaño que\(\mathbb{N}\)
un conjunto contable que tiene el mismo tamaño que\(\mathbb{N}\)
un conjunto que no es contable
- Un conjunto incontable es necesariamente infinito.
- Dos conjuntos que tienen el mismo tamaño (es decir, existe una biyección entre ellos) son ambos contables o ambos incontables.
Un conjunto no vacío\(A\) es contable si y solo si existe una secuencia de elementos a partir\(A\) de la cual cada elemento de\(A\) aparece exactamente una vez.
- Idea de Prueba.
-
En caso de\(A\) que sea finito, la afirmación es precisamente la de Hecho 12.2.1. Entonces supongamos que\(A\) es infinito, en cuyo caso una secuencia del tipo descrito en el enunciado también debe ser infinita. Técnicamente, una secuencia infinita de\(A\) es una función\(\mathbb{N} \to A\text{.}\) La propiedad “cada elemento de\(A\)” es lo mismo que decir que la función es suryectiva, y la propiedad “exactamente una vez” es lo mismo que decir que la función es inyectiva. Entonces, una secuencia del tipo descrito es exactamente la misma que la bijección,\(\mathbb{N} \to A\text{,}\) que es lo que se requiere\(A\) para que tenga el mismo tamaño que\(\mathbb{N}\) (es decir, contablemente infinita)
Compare este hecho con el hecho 12.2.1.
Conjuntos\(\mathbb{Z}\) y\(\mathbb{Q}\) son ambos contables.
- Prueba
-
Ya hemos construido una bijección\(\mathbb{N} \to \mathbb{Z}\) en el Ejemplo 12.3.1, que muestra que\(\mathbb{Z}\) es contable.
Para demostrar que\(\mathbb{Q}\) es contable, usaremos Fact\(\PageIndex{1}\) y construiremos una secuencia infinita que contenga cada elemento de una\(\mathbb{Q}\) sola vez. Primero, construya una cuadrícula infinita que contenga todos los números racionales positivos. Al zigzaguear a través de la cuadrícula, obtenemos una secuencia infinita que contiene cada elemento positivo de al\(\mathbb{Q}\) menos una vez, aunque hay duplicados porque un elemento de\(\mathbb{Q}\) puede tener muchas representaciones diferentes como fracción.

Figura\(\PageIndex{1}\): Una cuadrícula que contiene todos los números racionales positivos. 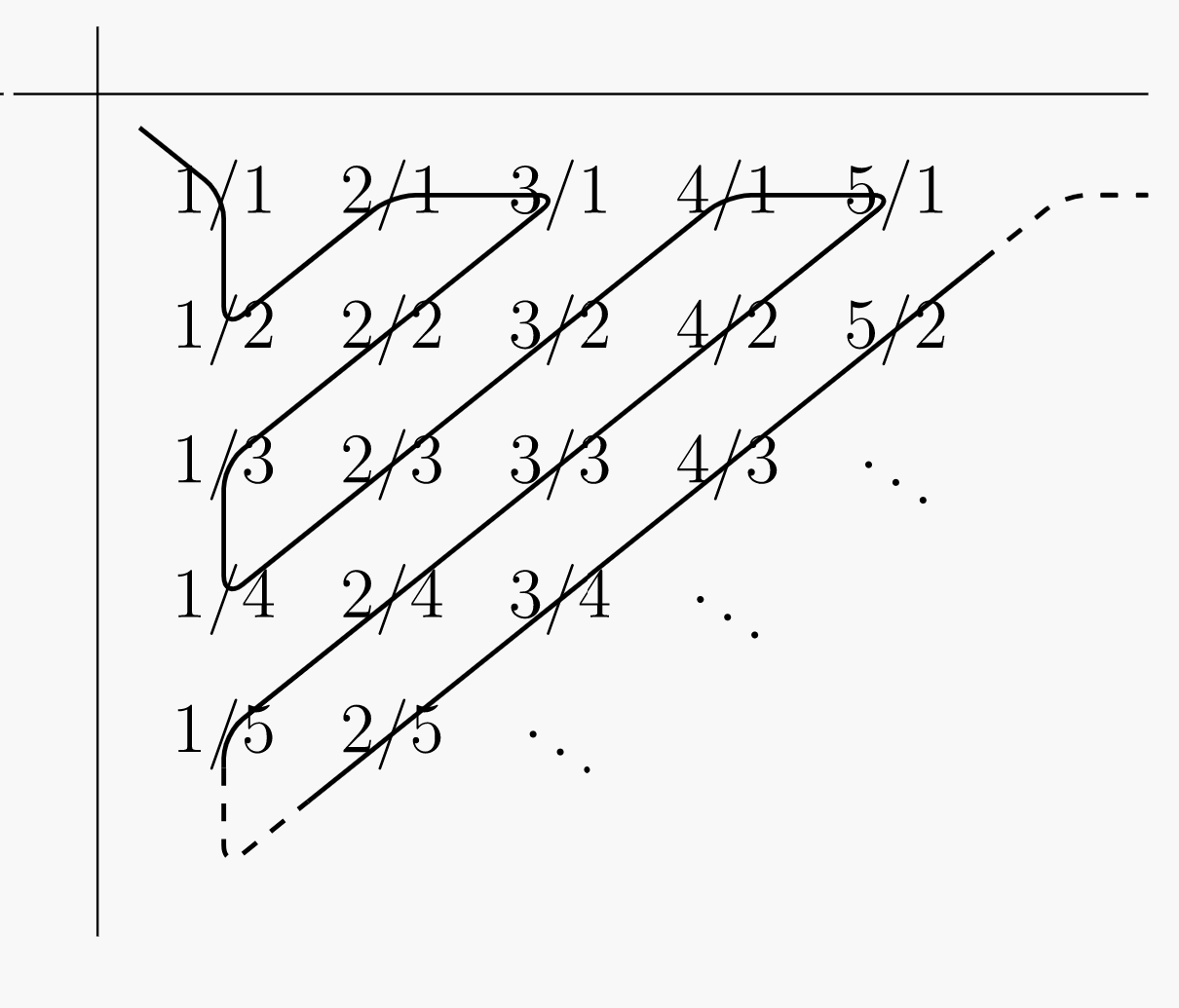
Figura\(\PageIndex{2}\): Un camino a través de los números racionales positivos. El camino a través de la cuadrícula crea la siguiente secuencia de números racionales positivos. Al tachar duplicados, obtenemos una secuencia infinita que contiene cada número racional positivo exactamente una vez.
\ begin {reunir*} 1,\;\;\;\ dfrac {1} {2},\;\;\; 2,\;\;\;\; 3,\;\;\;\;\ xcancel {1,}\;\;\;\ dfrac {1} {3},\;\;\;\ dfrac {1} {4},\;\;\;\;\ dfrac {2} {3},\;\;\;\ dfrac {3} {2},\;\;\; 4,\;\;\;\; 5,\\\ xcancel {2,}\;\;\;\ xcancel {1,}\;\;\;\ xcancel {\ dfrac {1} {2},}\;\;\;\ dfrac {1} {5},\;\;\;\ dfrac {1} {6},\;\;\;\ dfrac {2} {5},\ ;\;\;\ dfrac {3} {4},\;\;\;\ dfrac {4} {3},\;\;\;\ dfrac {5} {2},\;\;\;\;\ dotsc\ end {reunir*}Finalmente, intercalar los números racionales negativos en la secuencia anterior, e insertar\(0\) al principio.
\ begin {reunir*} 0,\;\;\;\;\; 1,\;\;\;\;\ dfrac {1} {2},\;\;\;\; -\ dfrac {1} {2},\;\;\; 2,\;\; -2,\;\;\;\; 3,\;\;;\;\ dfrac {1} {3},\;\;\; -\ dfrac {1} {3},\;\;\;\;\ dfrac {1} {4},\;\; -\ dfrac {1} {4},\;\;\;\ dfrac {2} {3},\;\; -\ dfrac {2} {3},\;\;\;\ dfrac {3} {2},\;\; -\ dfrac {3} {2},\;\;\; 4,\;\;\;\ ; -4,\;\;\; 5,\;\;\; -5,\;\;\;\;\ dotsc\ end {reunir*}
Aquí hay un ejemplo de un conjunto incontable. El argumento para probar que el conjunto es incontable es famoso, así que lo encapsulamos como la prueba de un Lema, en lugar de simplemente un Ejemplo sencillo.
Let\(\scr{C}\) representar el conjunto de todos los números reales entre\(0\) y\(0.2\) (incluyendo\(0\)) cuyas expansiones decimales implican sólo los dígitos\(0\) y\(1\text{.}\)
El conjunto\(\scr{C}\) es incontable.
- Prueba
-
El argumento en esta prueba se llama argumento diagonal de Cantor.
Mostraremos que ninguna secuencia de números de\(\scr{C}\) puede contener todos los elementos de\(\scr{C}\text{.}\)
Supongamos que\(\{a_k\}\) es una secuencia infinita de elementos de\(\scr{C}\text{.}\) Podemos crear un elemento\(r \in \scr{C}\) que no está en la secuencia de la siguiente manera. Set
\ begin {ecuación*} r = 0.r_1 r_2 r_3 r_4\ cdots\ text {,}\ end {ecuación*}
donde\(r_k\) está el dígito en el lugar\(k^{th}\) decimal de\(r\text{,}\) según las siguientes reglas.Si se\(0\text{,}\) establece la\(a_{k-1}\) posición\(k^{th}\) decimal de\(r_k = 1\text{.}\)
Si se\(1\text{,}\) establece la\(a_{k-1}\) posición\(k^{th}\) decimal de\(r_k = 0\text{.}\)
Claramente, cada dígito de\(r\) será un\(0\) o\(1\text{,}\) y\(0 \le r \lt 0.2\text{,}\) así\(r \in \scr{C}\text{.}\) (La razón que usamos en\(a_{k-1}\) lugar de\(a_k\) en las reglas para crear\(r\) es para asegurarnos de que consideramos el elemento de secuencia en\(a_0\) algún lugar de ahí.)
Ahora tenemos\(a_k \ne r\) para cada\(k \in \mathbb{N}\text{,}\) desde entonces\(r\) y\(a_k\) diferimos en el lugar\((k+1)^{th}\) decimal. Además,\(r \in \scr{C}\) debido a que está entre\(0\) y\(0.2\) y su expansión decimal implica solo dígitos\(0\) y\(1\text{.}\) Por lo tanto, la secuencia\(\{a_k\}\) no contiene todos los elementos de\(\scr{C}\) porque no contiene\(r\text{.}\)
- La parte “diagonal” del argumento diagonal del nombre Cantor se refiere a lo siguiente. Si las expansiones decimales de los números reales en la secuencia\(\{a_k\}\) se escriben en una cuadrícula para que cada fila sea uno de los números\(a_k\) y cada columna represente un lugar decimal específico en los números de secuencia, entonces las reglas a crear\(r\) pueden considerarse como “volteando” los dígitos que ocurren en las posiciones diagonales de esta cuadrícula. (¡Dibuja la cuadrícula por ti mismo para ver el patrón!)
- Posteriormente en este capítulo usaremos Lemma\(\PageIndex{1}\) para demostrar que\(\mathbb{R}\) en sí mismo es incontable. (Ver Teorema 13.2.1.)


