14.2: Propiedades de las Gráficas
- Page ID
- 117996
Propiedades de vértices y aristas
un borde que conecta un vértice consigo mismo
bordes que conectan los mismos vértices
sin bucles o bordes paralelos
conectado por un borde
compartir un vértice común
un par de vértice y borde donde el borde conecta el vértice ya sea a sí mismo o a otro vértice de la gráfica
un vértice que es incidente sin bordes
el número de veces que el vértice es incidente con un borde de la gráfica
grado de vértice\(v\)
En una gráfica simple, el grado de cada vértice es igual al número de aristas incidentes. Sin embargo, en una gráfica no simple, un bucle es incidente en su vértice dos veces, y contamos eso en el grado:
\ begin {ecuation*}\ text {deg} v =\ #\ {\ text {bordes que son incidentes con} v\ text {pero no bucles en} v\} + 2\ cdot\ #\ {\ text {bucles en} v\}. \ end {ecuación*}
La gráfica del Ejemplo 14.1.2 tiene las siguientes propiedades.
- Se trata de una gráfica sencilla.
- Cada par de vértices es adyacente.
- Cada par de bordes es adyacente pero no paralelo.
- No hay bucles.
- Cada vértice es incidente en dos bordes que no son de bucle, por lo que cada vértice tiene grado\(2\text{.}\)
La gráfica del Ejemplo 14.1.3 tiene las siguientes propiedades.
- No es una simple gráfica.
- Hay tres bordes paralelos que conectan\(v_1\) y\(v_2\text{.}\)
- Hay dos bucles en el vértice\(v_3\) (y estos también son bordes paralelos).
- Los bordes paralelos entre\(v_1\) y\(v_2\) son adyacentes, al igual que los dos bucles en\(v_3\text{.}\)
- Los vértices\(v_1\) y\(v_2\) son adyacentes, y el vértice\(v_3\) es adyacente a sí mismo.
- Los vértices\(v_1\) y\(v_2\) son incidentes a los tres bordes que corren entre ellos, y el vértice\(v_3\) es incidente a sus dos bucles.
- El vértice\(v_4\) está aislado
- Para titulaciones tenemos
\ begin {align*}\ text {deg} v_1 & =\ text {deg} v_2 = 3, &\ text {deg} v_3 & = 4, &\ text {deg} v_4 & = 0\ text {.} \ end {alinear*}
El número de aristas en una gráfica es una medida importante tanto de cuán “conectada” está la gráfica, como de cuánta “redundancia” contiene la gráfica.
el número de aristas en la gráfica\(G = (V,E)\)
Supongamos que\(G = (V,E)\) es una gráfica con vértice establecido\(V = \{ v_1, v_2, \ldots , v_n \}\text{.}\) Entonces,
\ begin {equation*}\ text {deg} v_1 +\ text {deg} v_2 +\ ldots\ text {deg} v_n = 2\ vert E\ vert. \ end {ecuación*}
- Idea de Prueba.
-
Si un borde\(e\) es un bucle en el vértice,\(v_i\text{,}\) entonces contribuye\(2\) a\(\text{deg} v_i\text{.}\) De lo contrario, si el borde\(e\) conecta vértices\(v_i\) y\(v_j\) (\(v_i \neq v_j\)), entonces contribuye\(1\) a cada uno de\(\text{deg} v_i\) y\(\text{deg} v_j\text{.}\) En cada caso, cada borde contribuye exactamente \(2\)a la suma de los grados de vértice.
En cada gráfica, el número de vértices de grado impar es par.
- Idea de Prueba.
-
De lo contrario, la suma de los grados de todos los vértices sería impar, lo que contradice el teorema anterior.
Un tipo impar organiza una fiesta extraña e invita a un número par de otras personas igualmente extrañas. Cada persona impar en la fiesta es amiga de un número impar de otras personas impares en la fiesta. ¿Es posible esta extraña fiesta?
Solución
Crea una gráfica simple con la gente de la fiesta como vértices, donde dos vértices están conectados por un solo borde si y sólo si las dos personas son amigas. Como cada persona tiene un número impar de amigos en la fiesta, el grado de cada vértice es impar. Pero el número de asistentes a la fiesta también es impar, ya que hay un número par de invitados, más el propio anfitrión. Entonces tenemos un número impar de vértices cada uno con grado impar, que el corolario anterior dice que no es posible.
Subgrafías
una gráfica que es parte de una gráfica más grande
gráfico\(G'\) es un subgrafo de gráfico\(G\)
Sin diagrama, ¿cómo podemos saber si una gráfica\(G' = (V',E')\) es una subgráfica de otra gráfica\(G = (V,E)\text{?}\) Primero, cada vértice de también\(G'\) debería ser un vértice de\(G\text{,}\) para que\(V' \subseteq V\text{.}\) Y además, cada borde de también\(G'\) debería aparecer como un borde en\(G\text{.}\) (Aunque no deberíamos simplemente escribir \(E' \subseteq E\text{,}\)y no sólo porque\(E'\) y en realidad\(E\) son conjuntos — ver Actividad 14.5.2.)
Así como\(\emptyset \subseteq A\) y\(A \subseteq A\) para cada conjunto\(A\text{,}\) que consideramos\((\emptyset,\emptyset) \preceq G\) y\(G \preceq G\) para cada gráfica\(G\text{.}\)
Determine todas las subgráficas posibles de la gráfica en el Ejemplo 14.1.2.
Solución
Primero, cada gráfica contiene la gráfica vacía como subgráfica. A continuación, una subgrafía no vacía de esta gráfica en particular puede contener uno, dos o los tres vértices. Podemos escribir todas las posibilidades no vacías de manera general en función del número de vértices en el subgrafo. En cada gráfica a continuación requerimos que los índices\(i, j, k\) de vértice sean todos distintos y que satisfagan\(1 \le i,j,k \le 3\text{.}\)
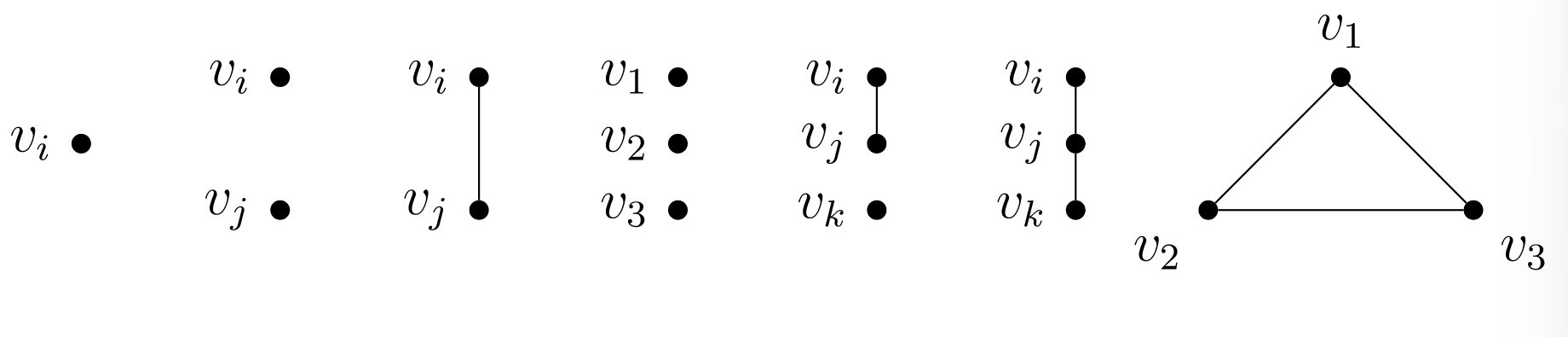
Hay\(3\) subgráficos de cada uno de los tres primeros tipos en la Figura\(\PageIndex{1}\). También hay\(3\) subgrafías de los tipos cuarto y quinto. Por lo tanto, incluyendo la gráfica vacía, hay\(18\) subgrafías de esta gráfica de ejemplo.
Gráficas completas
un gráfico en el que cada par de vértices distintos está conectado por exactamente un borde
- Las gráficas completas son simples.
- Para cada uno\(n \ge 0\text{,}\) hay una gráfica completa única\(K_n = (V,E)\) con\(\vert V \vert = n\text{.}\)
- Si\(n \ge 1\text{,}\) entonces cada vértice en\(K_n\) tiene grado\(n-1\text{.}\)
- Cada gráfico simple con\(n\) o menos vértices es un subgrafo de\(K_n\text{.}\)
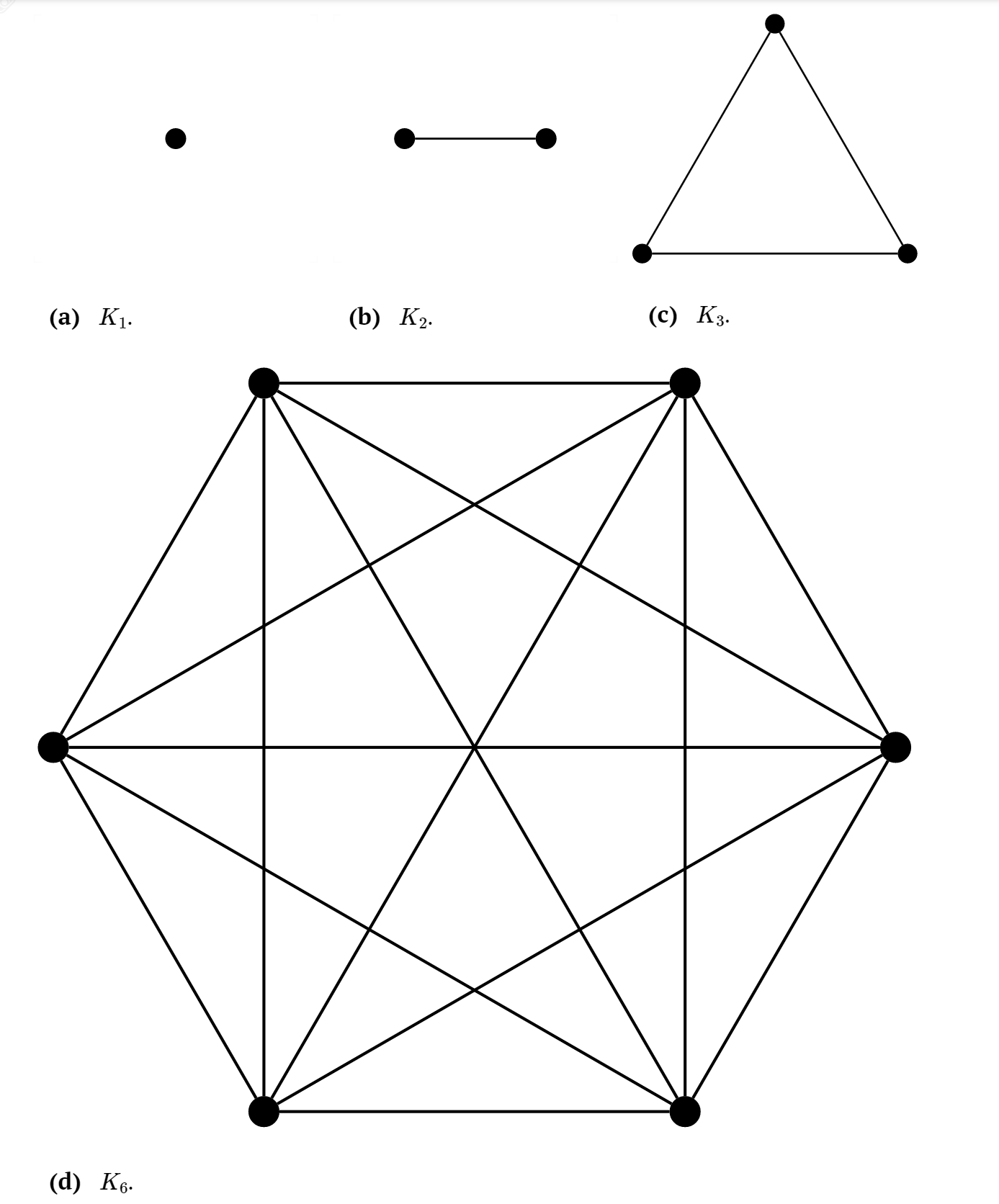
Dibuja las gráficas completas\(K_4\) y\(K_5\text{.}\)
¿Hay una gráfica completa\(K_0\text{?}\)


