14.3: Agregar información a las gráficas
- Page ID
- 118007
una gráfica en la que a cada borde se le asigna un peso o costo, generalmente un valor numérico
un triple ordenado\((V,E,w)\text{,}\) donde\((V,E)\) es una gráfica ordinaria y\(w: E \rightarrow W\) es una función con algún conjunto\(W\) como codominio
elementos de la imagen\(w(E) \subseteq W\)
Generalmente etiquetamos cada borde con su peso en diagramas para la gráfica.
Un mapa de carreteras con distancias como pesos es una gráfica ponderada. A continuación se muestra un mapa de ruta simplificado del área alrededor de Camrose, Alberta. El conjunto de vértices es el conjunto de ciudades, y el conjunto de bordes es el conjunto de autopistas. Por ejemplo, el conjunto de dos ciudades {Camrose, Edmonton} representa el borde en la gráfica entre Camrose y Edmonton, y corresponde a la autopista 21.
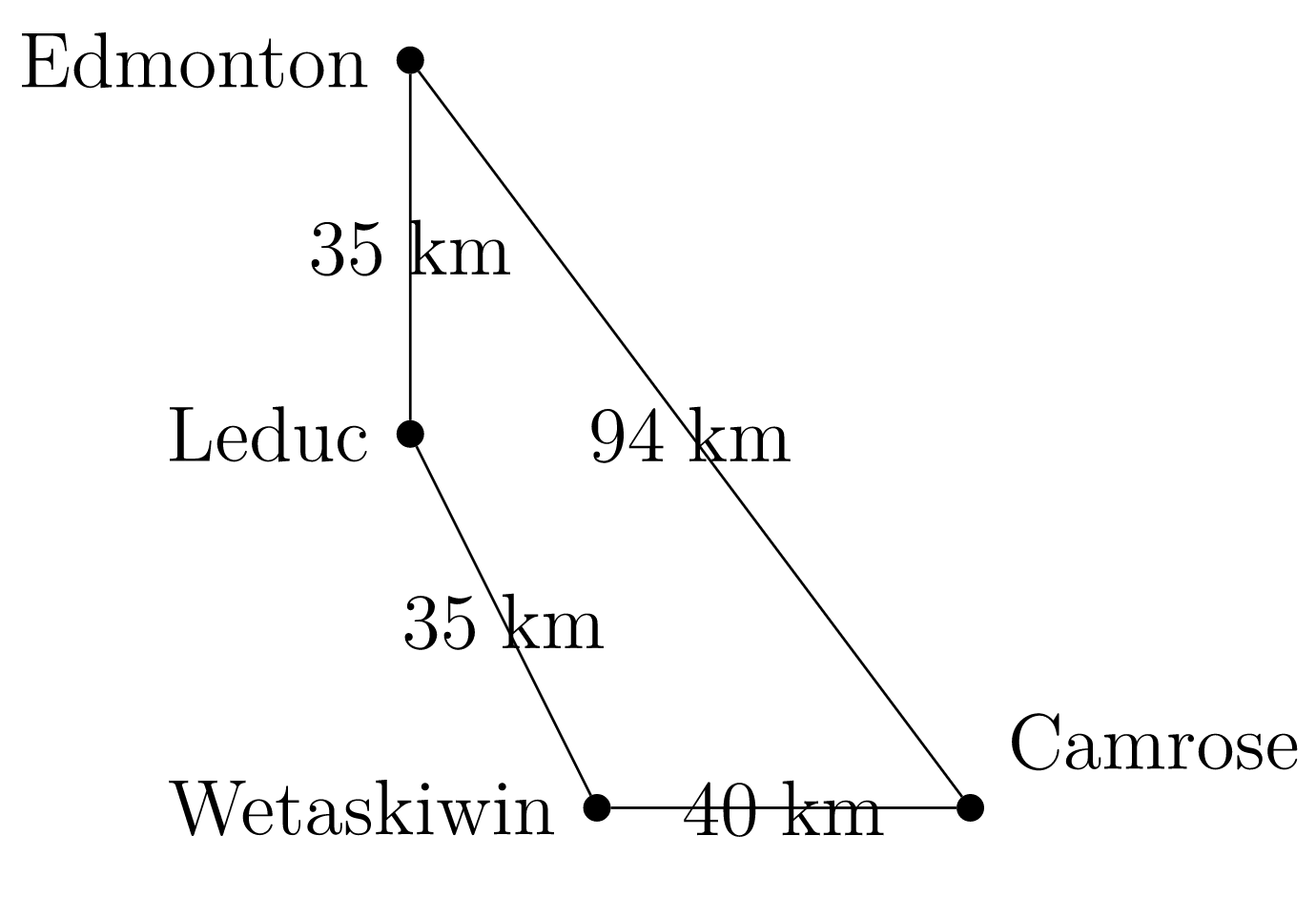
| \(e\) | \(w(e)\) |
| {Camrose, Edmonton} | \(94\) |
| {Edmonton, Leduc} | \(35\) |
| {Leduc, Wetaskiwin} | \(35\) |
| {Wetaskiwin, Camrose} | \(40\) |
Los bordes en la gráfica están ponderados por las distancias de carretera (redondeadas) entre ciudades. Formalmente, esta es una función\(w\) desde el conjunto de bordes hasta los números naturales. La relación entrada-salida que define esta función se tabula arriba a la derecha.
Las variaciones en Ejemplo\(\PageIndex{1}\) incluyen cualquier tipo de red de transporte o comunicación con líneas de transporte/comunicación como bordes. Los pesos posibles asignados a un borde incluyen: longitud de la línea; cantidad de tiempo que tarda un vehículo/mensaje en viajar a lo largo de la línea de un nodo al siguiente; capacidad de la línea en vehículos/pasajeros/mensajes/datos por unidad de tiempo; etc.
una gráfica en la que a cada borde se le puede dar una dirección, “apuntando” a uno de sus vértices incidentes
un par ordenado\((V,E)\text{,}\) donde\(V\) es un conjunto finito y\(E\) es una lista desordenada, posiblemente vacía de elementos de\(V \times V\)
Nuevamente, elementos de\(V\) son los vértices y elementos de\(E\) son los bordes de la gráfica. Para una gráfica ordinaria, las aristas estaban representadas por subconjuntos de\(V\) porque al especificar una arista, el orden de los vértices que van a ser incidentes con el borde es irrelevante. Para una gráfica dirigida, el orden de los vértices incidentes a un borde ahora importa, por lo que usamos pares ordenados de vértices para especificar una arista. Si\(e = (v,v') \in E\) para algunos\(v,v' \in V\text{,}\) consideran la dirección\(e\) de ser\(v \to v'\text{.}\)
Considerar
\ begin {reunir*} V =\ {v_1, v_2, v_3, v_4\},\\ E =\ {(v_1, v_2), (v_1, v_2), (v_2, v_3), (v_3, v_2), (v_4, v_3), (v_4, v_4)\}. \ end {reunir*}
Dibujamos la gráfica\(G = (V,E)\) con flechas para indicar la dirección de los bordes.

Inventar una definición formal para gráfica dirigida y ponderada.


