18.7: Ejercicios

Última actualización
Guardar como PDF

Page ID: 118275

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Ejercicio\(\PageIndex{1}\)

Dejar\(\mathord{\equiv}\) representar la relación sobre\(\mathbb{R}\times\mathbb{R}\) dónde\((x_1,y_1) \equiv (x_2,y_2)\) significa\(y_1 - x_1^2 = y_2 - x_2^2\text{.}\)

Verificar que\(\mathord{\equiv}\) sea una relación de equivalencia.
Describir las clases de equivalencia\([(0,0)]\text{,}\)\([(0,1)]\text{,}\) y\([(1,0)]\) geométricamente como conjuntos de puntos en el plano.

Ejercicio\(\PageIndex{2}\)

Dada una gráfica conectada (no dirigida)\(G\text{,}\) podemos definir una relación sobre el conjunto\(V\) de vértices de la\(G\) siguiente manera:\(v_1 R v_2\) digamos que existe un rastro dentro de\(G\) principio en vértice\(v_1\) y terminando en vértice\(v_2\) que atraviesa un número par de aristas.

Demostrar que\(R\) es una relación de equivalencia en\(V\text{.}\)
Determinar las clases de equivalencia para esta relación cuando\(G\) es la gráfica a continuación.

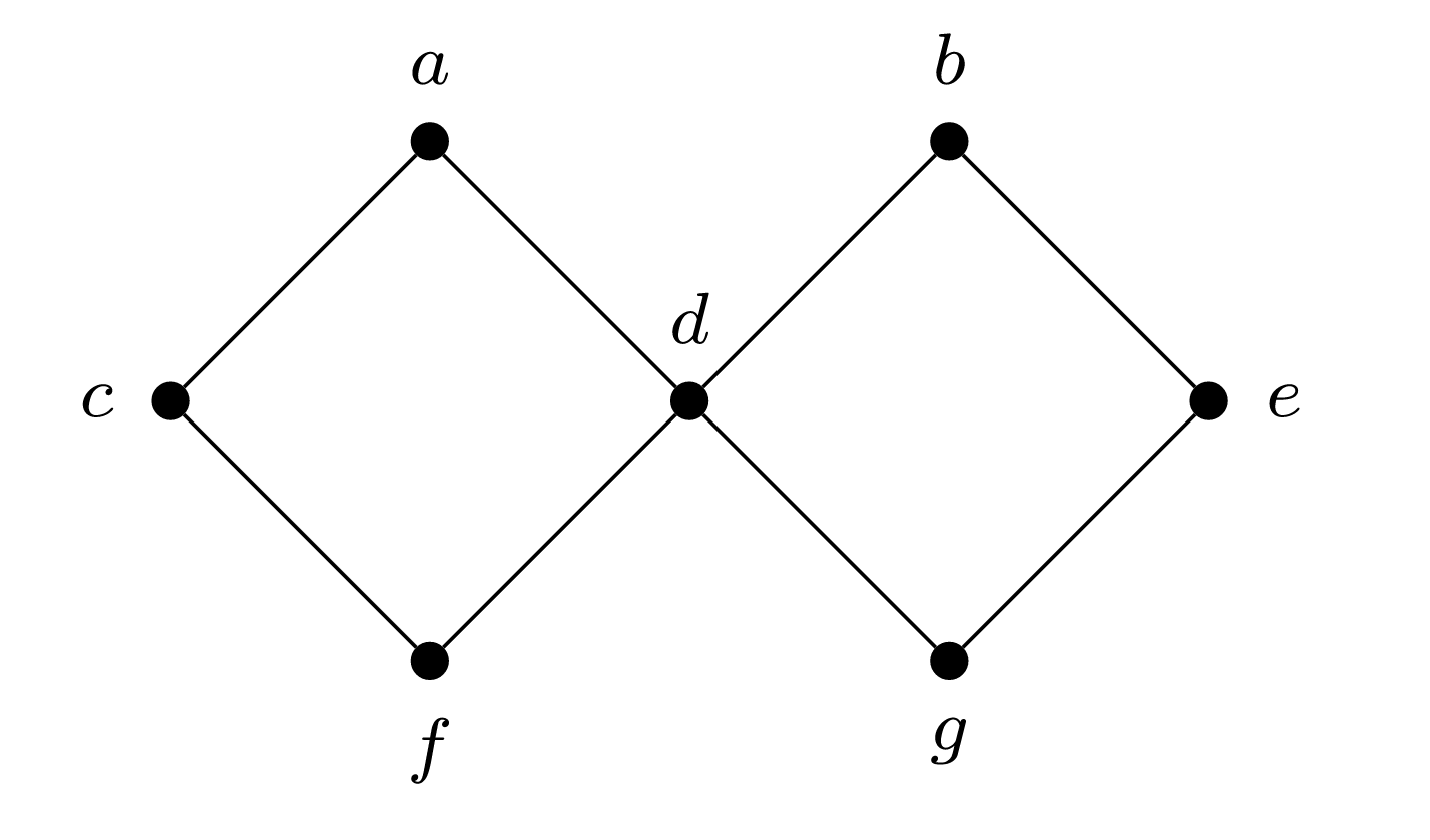
Relaciones de equivalencia y clases.

En cada uno de los Ejercicios 3—12, se le da un conjunto\(A\) y una relación\(R\) sobre\(A\text{.}\) Determinar si\(R\) es una relación de equivalencia, y, en su caso, describir sus clases de equivalencia. Trate de ser más descriptivo que solo “\([a]\)es el conjunto de todos los elementos que son equivalentes a\(a\text{.}\)”

Ejercicio\(\PageIndex{3}\)

\(A = \{a, b, c\} \text{;}\)\(R = \{(a,a),(b,b),(c,c),(a,b),(b,a)\} \text{.}\)

Ejercicio\(\PageIndex{4}\)

\(A = \{-1, 0, 1\} \text{;}\)\(R = \{(x,y) | x^2 = y^2\} \text{.}\)

Ejercicio\(\PageIndex{5}\)

\(A\)es el conjunto de potencia de algún conjunto;\(R\) es la relación de subconjunto.

Ejercicio\(\PageIndex{6}\)

\(A = \mathbb{R} \text{;}\)\(x_1 \mathrel{R} x_2 \)significa\(f(x_1) = f(x_2) \text{,}\) dónde\(f: \mathbb{R} \rightarrow \mathbb{R}\) está la función\(f(x) = x^2 \text{.}\)

Ejercicio\(\PageIndex{7}\)

\(A\)es un conjunto abstracto;\(a_1 \mathrel{R} a_2\) significa\(f(a_1) = f(a_2)\text{,}\) donde\(f: A \rightarrow B\) es una función arbitraria con dominio\(A\text{.}\)

Ejercicio\(\PageIndex{8}\)

\(A\)es el conjunto de todas las expresiones “formales”\(a/b\text{,}\) donde\(a,b\) son enteros y\(b\) es distinto de cero;\((a/b) \mathrel{R} (c/d) \) significa\(ad = bc \text{.}\)

Nota: No pienses\(a/b\) como una fracción de la manera habitual; en cambio, piensa en ella como una colección de símbolos que consiste en dos enteros en un orden específico con una diagonal hacia delante entre ellos.

Ejercicio\(\PageIndex{9}\)

\(A\)es el conjunto de potencia de algún conjunto finito;\(X \mathrel{R} Y\) significa\(\vert X \vert = \vert Y \vert \text{.}\)

Ejercicio\(\PageIndex{10}\)

\(A\)es el conjunto de todas las líneas rectas en el plano;\(L_1 \mathrel{R} L_2\) media\(L_1\) es paralela a\(L_2\text{.}\)

Ejercicio\(\PageIndex{11}\)

\(A\)es el conjunto de todas las líneas rectas en el plano;\(L_1 \mathrel{R} L_2\) media\(L_1\) es perpendicular a\(L_2\text{.}\)

Ejercicio\(\PageIndex{12}\)

\(A = \mathbb{R} \times \mathbb{R} \text{;}\)\((x_1,y_1) \mathrel{R} (x_2,y_2)\)significa\(x_1^2 + y_1^2 = x_2^2 + y_2^2 \text{.}\)

Pista.: ¿La expresión te\(x^2 + y^2\) recuerda algo desde la geometría?