19.5: Elementos Máximos/Mínimos

Cada una de las siguientes definiciones son para un subconjunto\(B\) de un conjunto parcialmente ordenado\(A\text{.}\)

Definición: Entero superior

un elemento\(u \in A\) tal que\(b \preceq u\) para todos\(b \in B\)

Definición: Mínimo límite superior

un límite superior para\(B \subseteq A\) eso es menor que cualquier otro límite superior

Definición: Elemento máximo

un límite superior para\(B\) eso está contenido en\(B\)

Definición: Inferior

un elemento\(\ell \in A\) tal que\(\ell \preceq b\) para todos\(b \in B\)

Definición: Mayor límite inferior

un límite inferior para\(B \subseteq A\) eso es mayor que cualquier otro límite inferior

Definición: Elemento mínimo

un límite inferior para\(B\) eso está contenido en\(B\)

Advertencia\(\PageIndex{1}\)

1. Un límite superior o inferior no necesita pertenecer al subconjunto para el que es un límite.
2. Un conjunto (o subconjunto) no necesariamente tiene un elemento máximo o mínimo.

Hecho\(\PageIndex{1}\)

Si un subconjunto de un conjunto parcialmente ordenado contiene un elemento máximo, entonces ese elemento máximo es único. Y de manera similar para un elemento mínimo.

Comprobante.

Se le pide que demuestre esto en la Actividad 19.7.5.

Ejemplo\(\PageIndex{1}\): Maximums, minimums, and bounds in \(\mathbb{R}\).

Considere el pedido habitual (total)\(\mathord{\leq}\) en\(\mathbb{R}\text{.}\)

• El conjunto completo no\(\mathbb{R}\) tiene ni un elemento máximo ni mínimo.
• El subconjunto\((0,1)\) tiene muchos límites superiores (cualquier cosa\(\geq 1\)) y muchos límites inferiores (cualquier cosa\(\leq 0\)). Sin embargo, nos referiríamos\(1\) como el menor boun d superior y\(0\) como el mayor límite inferior de\((0,1)\text{.}\)
• El subconjunto no\((0,1)\) tiene ningún elemento máximo o mínimo. Sin embargo, el subconjunto\([0,1]\) tiene máximo\(1\) y mínimo\(0\text{.}\)

Ejemplo\(\PageIndex{2}\): Maximums, minimums, and bounds in a power set.

Supongamos que\(U\) es un conjunto universal, y considerar\(\mathscr{P}(U)\) parcialmente ordenado por\(\mathord{\subseteq}\) como de costumbre. En el conjunto completo\(\mathscr{P}(U)\text{,}\) el elemento máximo único es\(U\text{,}\) que es solo otra forma de decir que cada elemento de\(\mathscr{P}(U)\) es un subconjunto de\(U\text{.}\) Y el elemento mínimo único es\(\emptyset\text{,}\) que es solo otra forma de decir que el conjunto vacío es un subconjunto de cada subconjunto de\(U\text{.}\)

Ahora considera un subconjunto\(\mathscr{A} \subseteq \mathscr{P}(U)\text{,}\) para que\(\mathscr{A}\) sea una colección de subconjuntos de\(U\text{.}\) Debido a la existencia de elementos máximos y mínimos, estos elementos también sirven como límite superior e inferior, respectivamente, para\(\mathscr{A}\text{.}\) Sin embargo, también se puede encontrar un límite superior mínimo para\(\mathscr{A}\) tomando la unión de todos los subconjuntos de\(U\) contenidos en\(\mathscr{A}\text{,}\) y uno puede encontrar un límite inferior mayor tomando la intersección de todos los subconjuntos de\(U\) contenidos en\(\mathscr{A}\text{.}\)

Las dos definiciones siguientes se establecen para elementos en un conjunto parcialmente ordenado, pero también podrían entenderse para elementos en un subconjunto de un conjunto parcialmente ordenado, ya que cada subconjunto de un conjunto parcialmente ordenado también es un conjunto parcialmente ordenado.

Definición: Maximal Element

un elemento para el que ningún otro elemento es mayor

Definición: Minimal Element

un elemento para el que ningún otro elemento es menor

Comentario\(\PageIndex{1}\)

La diferencia entre máximo y máximo es sutil. Un elemento máximo debe ser mayor que (y por lo tanto comparable a) cualquier otro elemento de\(A\text{,}\) mientras que un elemento máximo solo debe ser mayor que cualquier otro elemento\(A\) al que sea comparable. La distinción entre mínimo y mínimo es similar.

Test\(\PageIndex{1}\): Maximal/minimal elements.

1. Para verificar que\(\overline{m} \in A\) es máximo, probar o bien la definición original

\ begin {equation*} (\ forall x\ in A) ({x\ neq\ overline {m}}\ Rightarrow {\ overline {m}\ npreceq x})\ text {,}\ end {equation*}
o probar la formulación contrapositiva equivalente
\ begin {equation*} (\ forall x\ in A) ({\ overline {m}\ preceq x}\ Rightarrow {x =\ overline {m}})\ text {.} \ end {ecuación*}

 

2. Para verificar que\(\underline{m} \in A\) es mínimo, probar ya sea la definición original

\ begin {equation*} (\ forall x\ in A) ({x\ neq\ subrayado {m}}\ Rightarrow {x\ npreceq\ subrayado {m}})\ text {,}\ end {ecuación*}
o probar la formulación contrapositiva equivalente
\ begin {ecuación*} (\ forall x\ in A) ({x\ preceq\ subrayado {m}}\ Fila derecha {x =\ subrayado {m}})\ texto {.} \ end {ecuación*}

Ejemplo\(\PageIndex{3}\): Connected components are maximal.

Considera la gráfica\(G\) en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Un ejemplo de gráfico no conectado.

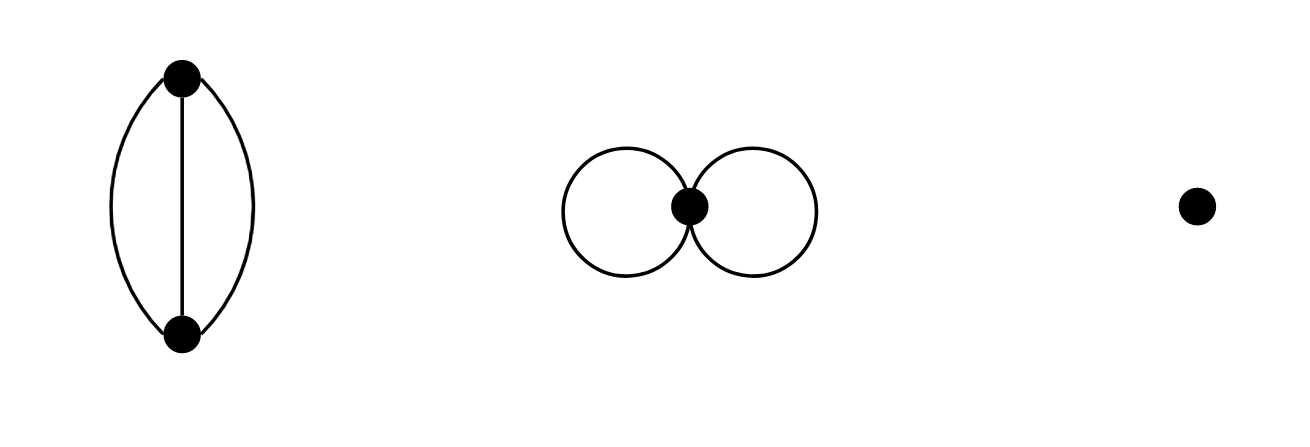
Dejar\(S(G)\) representar la colección de subgrafías de\(G\text{,}\) parcialmente ordenadas por la relación subgráfica. (Por mi cuenta,\(\vert S(G) \vert = 110\text{.}\)) Dejar\(C(G)\) representar la colección de subgrafías conectadas de\(G\text{.}\) (Por mi cuenta,\(\vert C(G) \vert = 15\text{.}\)) Un elemento máximo de\(C(G)\) tendría que ser un subgrafo conectado de\(G\) que está contenido en no más grande subgrafía conectada de\(G\) — pero este es precisamente el definición de componente conectado. De ahí\(C(G)\) que tenga tres elementos máximos, los tres componentes conectados que ve en la Figura\(\PageIndex{1}\). Sin embargo, un elemento máximo de\(C(G)\) sería un subgrafo conectado del\(G\) cual contiene todos los demás subgrafos conectados de\(G\text{,}\) y la existencia de múltiples componentes conectados en este ejemplo gráfico no conectado hace imposible dicho subgrafo.

Comentario\(\PageIndex{2}\)

Si compara tanto nuestra definición informal como la definición formal de componente conectado con nuestra definición de elemento máximo y nuestra Prueba de Elementos Máximos/Mínimos, debería encontrar que la definición de componente conectado significa precisamente un subgrafo máximo con respecto a la propiedad de estar conectado.

Ejemplo\(\PageIndex{4}\)

Dejar\(A = \{a,b,c\}\text{.}\) Dado el diagrama de Hasse para\(\mathord{\subseteq}\) on\(P = \mathscr{P}(A)\setminus\{A\}\) en la Figura\(\PageIndex{2}\), determinar todos los elementos máximo/máximo/mínimo/mínimo, si existen.

Figura\(\PageIndex{2}\): El diagrama de Hasse para\(\subseteq\) un conjunto de potencia “sin tapa”

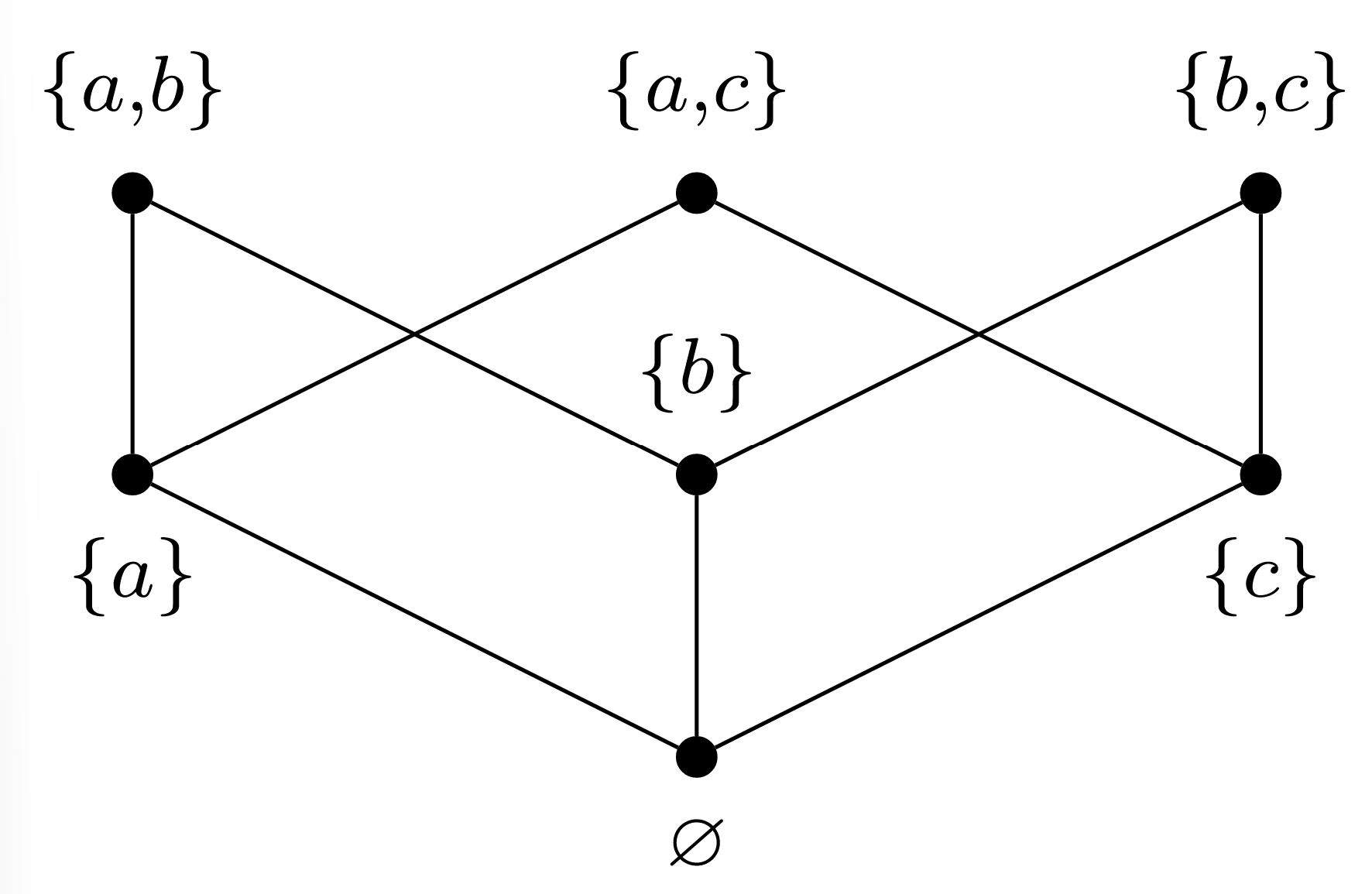
Solución

El elemento\(\{a,b\}\) es máximo, ya que cada nodo en el diagrama de Hasse que es adyacente a\(\{a,b\}\) está por debajo de él. El mismo razonamiento confirma que\(\{a,c\}\text{,}\) y\(\{b,c\}\) de son también máximos. No obstante, ninguno de ellos es máximo, ya que ninguno de ellos es mayor que los otros dos.

El elemento\(\emptyset\) de\(P\) es un elemento mínimo, ya que cada nodo que es adyacente a él está por encima de él. Y es el único elemento mínimo. Además,\(\emptyset\) es el elemento mínimo, ya que por cada otro nodo hay un paseo hacia arriba desde\(\emptyset\) ese nodo.

Advertencia\(\PageIndex{2}\)

El simple hecho de dibujar un nodo más alto o más bajo en un diagrama de Hasse no necesariamente lo hace más grande o más pequeño, respectivamente, cuando se compara con otros elementos a través del orden parcial. Por ejemplo, en el diagrama de Hasse de Figura\(\PageIndex{2}\), podríamos haber dibujado el nodo para\(\{a,c\}\) en una ubicación más alta, pero eso no lo haría más grande que\(\{a,b\}\) y\(\{b,c\}\text{,}\) ya que todavía no habría habido bordes o cadenas de bordes de\(\{a,c\}\) abajo a esos otros dos nodos.

Hecho\(\PageIndex{2}\)

Si el conjunto parcialmente ordenado\(A\) tiene un elemento máximo, entonces ese elemento también es el único elemento máximo de\(A\text{.}\) Similarmente, el elemento mínimo, si existe, es el único elemento mínimo de\(A\text{.}\)

Idea de Prueba.

Supongamos que\(A\) tiene un elemento máximo. Entonces cada elemento de\(A\) es comparable y menor que ese elemento máximo, por lo que ningún elemento es más grande que él. Por lo tanto, este máximo debe ser máximo. Y ningún otro elemento podría ser máximo, porque para ser medios máximos no hay elementos que sean más grandes. Pero nuestro elemento máximo siempre es mayor.

Advertencia\(\PageIndex{3}\)

Un elemento máximo debe ser máximo y debe ser el único máximo. Pero un elemento máximo, aunque sea el único, no necesita ser el máximo.

Ejemplo\(\PageIndex{5}\): A partially ordered set with exactly one maximal element but no maximum element

Considerar

\ begin {ecuación*} A =\ {3\}\ copa\ {2,4,8,16,32,64,\ ldots,2^n,\ ldots\},\ end {ecuación*}
parcialmente ordenado por\(\mathord{\mid}\text{,}\) la relación “divide”. No hay elemento de\(A\) que sea divisible por\(3\) (excepto por\(3\) sí mismo), por lo que no hay elemento de\(A\) que sea mayor que\(3\text{.}\) Por lo tanto,\(3\) es máximo. Además,\(3\) es el único elemento máximo en\(A\text{,}\) ya que cada poder de\(2\) divide el siguiente poder de\(2\text{.}\) Sin embargo, no hay elemento máximo en\(A\text{,}\) ya que no hay elemento del\(A\) cual sea divisible por todos los demás elementos de\(A\text{.}\)

Ejemplo\(\PageIndex{6}\): A partially ordered set with infinitely many maximal/minimal elements but no maximum/minimum element.

Considera\(\mathscr{A} \subsetneqq \mathscr{P}(\mathbb{N})\text{,}\) dónde

\ begin {ecuación*}\ mathscr {A} =\ mathscr {P} (\ mathbb {N})\ setmenos\ {\ conjunto vacío,\ mathbb {N}\}\ text {.} \ end {equation*}
Así\(\mathscr{A}\) es el conjunto de todos los subconjuntos no vacíos, propios de\(\mathbb{N}\text{.}\) Bajo el orden parcial no\(\mathord{\subseteq}\text{,}\)\(\mathscr{A}\) tiene ni un elemento máximo ni mínimo, pero para cada\(n \in \mathbb{N}\text{,}\)\(\{n\}\) es un elemento mínimo y\(\mathbb{N} \setminus \{n\}\) es un elemento máximo de\(\mathscr{A}\text{.}\)