19.6: Clasificación Topológica
- Page ID
- 118264
A veces queremos convertir una orden parcial en una orden total. Lo que hace que un orden sea parcial en lugar de total es la presencia de pares de elementos incomparables. Entonces, para convertir nuestro orden parcial en un orden total solo necesitamos imponer una relación de orden a esos pares de elementos previamente incomparables. No obstante, para cada par de elementos incomparables hay que elegir cuál se convertirá en el más pequeño y cuál más grande en el nuevo orden total. Y no podemos llevar a cabo estas elecciones de manera totalmente arbitraria, porque corremos el riesgo de contradecir las propiedades requeridas de un orden parcial (ver Ejemplo\(\PageIndex{1}\)).
Las siguientes definiciones se aplican a un orden parcial\(\mathord{\preceq}\) en un conjunto\(A\text{.}\)
Definición: Pedido Total Compatible
un pedido total\(\mathord{\le}\) en\(A\) tal que si\(a_1 \preceq a_2\) entonces\(a_1 \le a_2\)
Definición: Clasificación Topológica
un proceso para determinar un pedido total compatible
Ejemplo\(\PageIndex{1}\): A failed attempt at topological sorting.
La relación\(\mathord{\subseteq}\) on\(\mathscr{P}(\mathbb{N})\) es un orden parcial pero no un orden total. Consideremos lo que sucede cuando comenzamos a tratar de construir un orden total\(\mathscr{P}(\mathbb{N})\) a partir\(\mathord{\subseteq}\) de la elección arbitraria de las relaciones entre elementos previamente incomparables.
- Los elementos\(\{1\},\{2,3\}\) son\(\mathord{\subseteq}\) -incomparables; elegir\(\{2,3\} \le \{1\}\text{.}\)
- Los elementos\(\{1\},\{2\}\) son\(\mathord{\subseteq}\) -incomparables; elegir\(\{1\} \le \{2\}\text{.}\)
- ...
Ahora, ya\(\{2\} \subseteq \{2,3\}\) es cierto, así que para ser compatibles debemos fijarnos\(\{2\} \leq \{2,3\}\) en el nuevo orden total. Pero ahora\(\{1\} \leq \{2\} \leq \{2,3\}\) dictaría\(\{1\} \leq \{2,3\}\) satisfacer la propiedad transitiva, pero esto contradice nuestra primera elección arbitraria anterior.
Si\(A\) es contable, ya sea finito o contablemente infinito, entonces especificando un orden total en\(A\) cantidades para escribir los elementos de\(A\) en una lista ordenada. (Ver Ejemplo 19.4.6 y Observación 19.4.7.) En ese caso, la clasificación topológica equivale a crear tal lista ordenada de manera que si\(a \preceq b\) entonces\(a\) aparece antes\(b\) en la lista.
Si\(A\) es un conjunto finito parcialmente ordenado con respecto a\(\mathord{\preceq}\text{,}\) podemos especificar un orden total compatible\(\mathord{\leq}\) en\(A\) escribiendo los elementos de\(A\) en una lista
\ begin {ecuación*} a_0\ leq a_1\ leq\ cdots\ leq a_ {n-1}\ end {ecuación*} de la
siguiente manera, donde\(n = \vert A \vert\text{.}\)
- Inicializar\(i = 0\) y\(A_0 = A\text{.}\)
- Elija un elemento mínimo de\(A_i\text{;}\) let\(a_i\) representar el elemento elegido.
- Set\(A_{i+1} = A_i \setminus \{a_i\}\) (es decir, crear un conjunto más pequeño parcialmente ordenado descartando\(a_i\)).
- Incremento\(i\) por\(1\text{.}\) Si\(i \lt n\) luego regresa al Paso 2. De lo contrario, si\(i = n\) entonces ahora\(A_i\) debería estar vacío, así que deténgase — ahora se ha especificado el orden compatible deseado.
En el Paso 2 del algoritmo, si\(A_i\) contiene un elemento mínimo, entonces debes elegir ese elemento, ya que en ese caso no puede existir ningún otro elemento mínimo (ver el Hecho 19.5.2).
Ejemplo\(\PageIndex{1}\)
Considerar
\ begin {ecuación*} A =\ mathscr {P} (\ {0,1,2\}) =\ bigl\ {\ juego vacío,\ {0\},\ {1\},\ {2\},\ {0,1\},\ {0,2\},\ {1,2\},\ {0,1,2\}\ bigr\}\ texto {.} \ end {equation*}
Aplica Algoritmo\(\PageIndex{1}\) para determinar un pedido\(\mathord{\leq}\) total\(A\) que sea compatible con\(\mathord{\subseteq}\text{.}\)
Solución. 1 Solución de algoritmo
En\(A_0 = A\text{,}\) debemos elegir\(a_0 = \emptyset\text{,}\) ya que es el mínimo. Ahora retire\(a_0\) para que
\ begin {ecuación*} A_1 =\ bigl\ {\ {0\},\ {1\},\ {2\},\ {0,1\},\ {0,2\},\ {1,2\},\ {0,1,2\}\ bigr\}. \ end {equation*}
Elige un elemento mínimo de\(A_1\text{:}\) let\(a_1 = \{2\}\text{.}\) Now remove\(a_1\text{;}\) set
\ begin {ecuación*} A_2 =\ bigl\ {\ {0\},\ {1\},\ {0,1\},\ {0,2\},\ {1,2\},\ {0,1,2\}\ bigr\}. \ end {equation*}
Elige un elemento mínimo de\(A_2\text{:}\) let\(a_2 = \{0\}\text{.}\) Now remove\(a_2\text{;}\) set
\ begin {ecuación*} A_3 =\ bigl\ {\ {1\},\ {0,1\},\ {0,2\},\ {1,2\},\ {0,1,2\}\ bigr\}. \ end {equation*}
Elige un elemento mínimo de\(A_3\text{:}\) let\(a_3 = \{0,2\}\text{.}\) Now remove\(a_3\text{;}\) set
\ begin {ecuación*} A_4 =\ bigl\ {\ {1\},\ {0,1\},\ {1,2\},\ {0,1,2\}\ bigr\}. \ end {equation*}
Debemos elegir\(a_4 = \{1\}\text{,}\) ya que es el mínimo en\(A_4\text{.}\) Ahora eliminar\(a_4\text{;}\) conjunto
\ begin {ecuación*} A_5 =\ bigl\ {\ {0,1\},\ {1,2\},\ {0,1,2\}\ bigr\}. \ end {equation*}
Escoge un elemento mínimo de\(A_5\text{:}\) let\(a_5 = \{1,2\}\text{.}\) Ahora eliminar\(a_5\text{;}\) conjunto\(A_6 = \bigl\{ \{0,1\}, \{0,1,2\} \bigr\}\text{.}\) Debemos elegir\(a_6 = \{0,1\}\text{,}\) ya que es el mínimo en\(A_6\text{.}\) Solo queda un elemento; establecer\(A_7 = \bigl\{ \{0,1,2\} \bigr\}\) y elegir\(a_7 = \{0,1,2\}\text{.}\) Así que tenemos
\ begin {ecuación*}\ juego vacío\ leq\ {2\}\ leq\ {0\}\ leq\ {0,2\}\ leq\ {1\}\ leq\ {1,2\}\ leq\ {0,1\}\ leq\ {0,1,2\}. \ end {equation*}
Observe que el elemento máximo de\(A\) terminó en la “parte superior” del orden total y el elemento mínimo fue forzado a la “parte inferior”.
Solución. 2 Solución gráfica
Podemos realizar el algoritmo de clasificación topológica gráficamente; en cada paso, elegir un vértice que no tenga vértices adyacentes debajo de él en la gráfica, luego cruzar ese vértice y cualquier borde adyacente fuera de la gráfica.
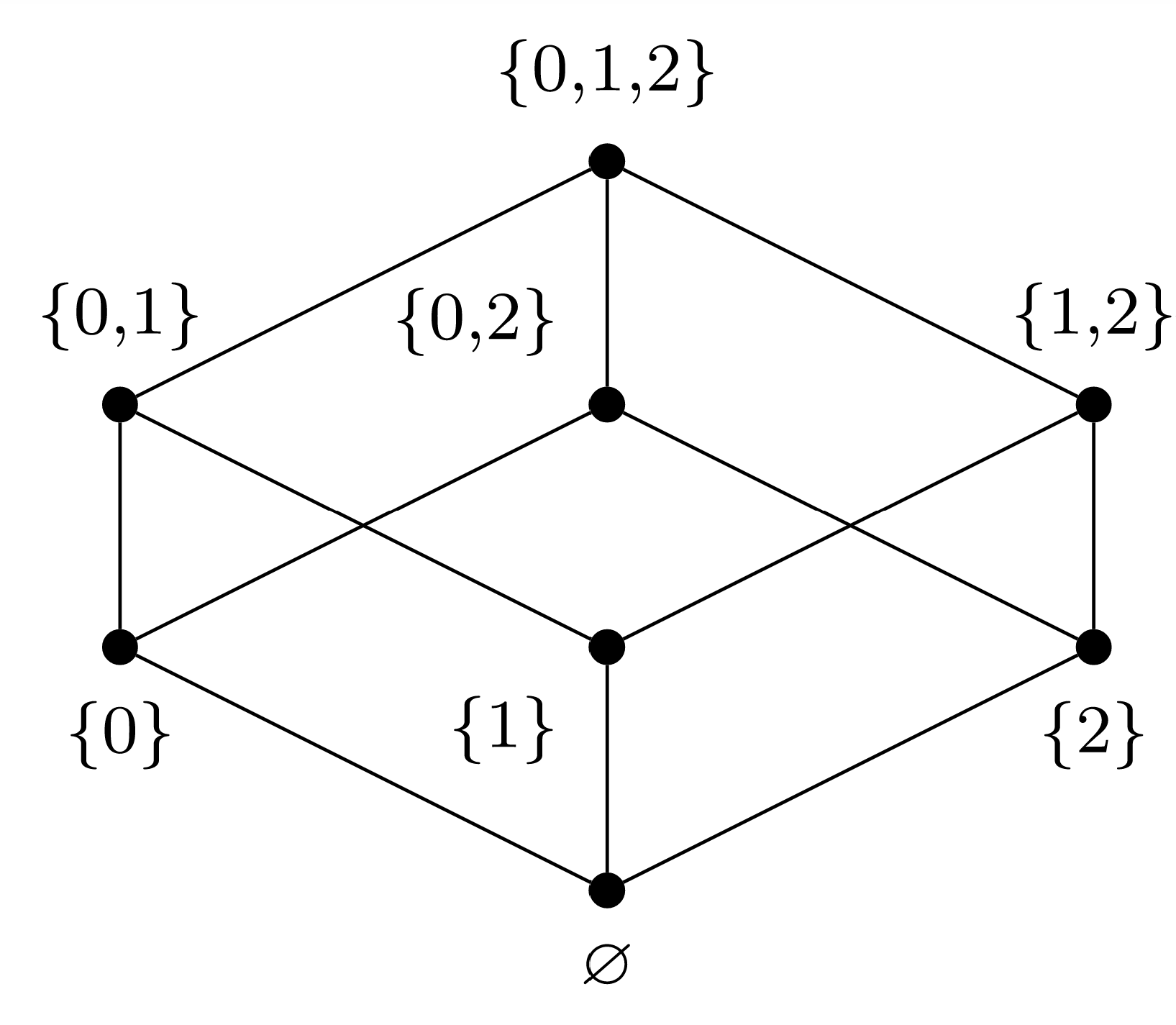
(a) Elegir\(a_0 = \emptyset\text{.}\)
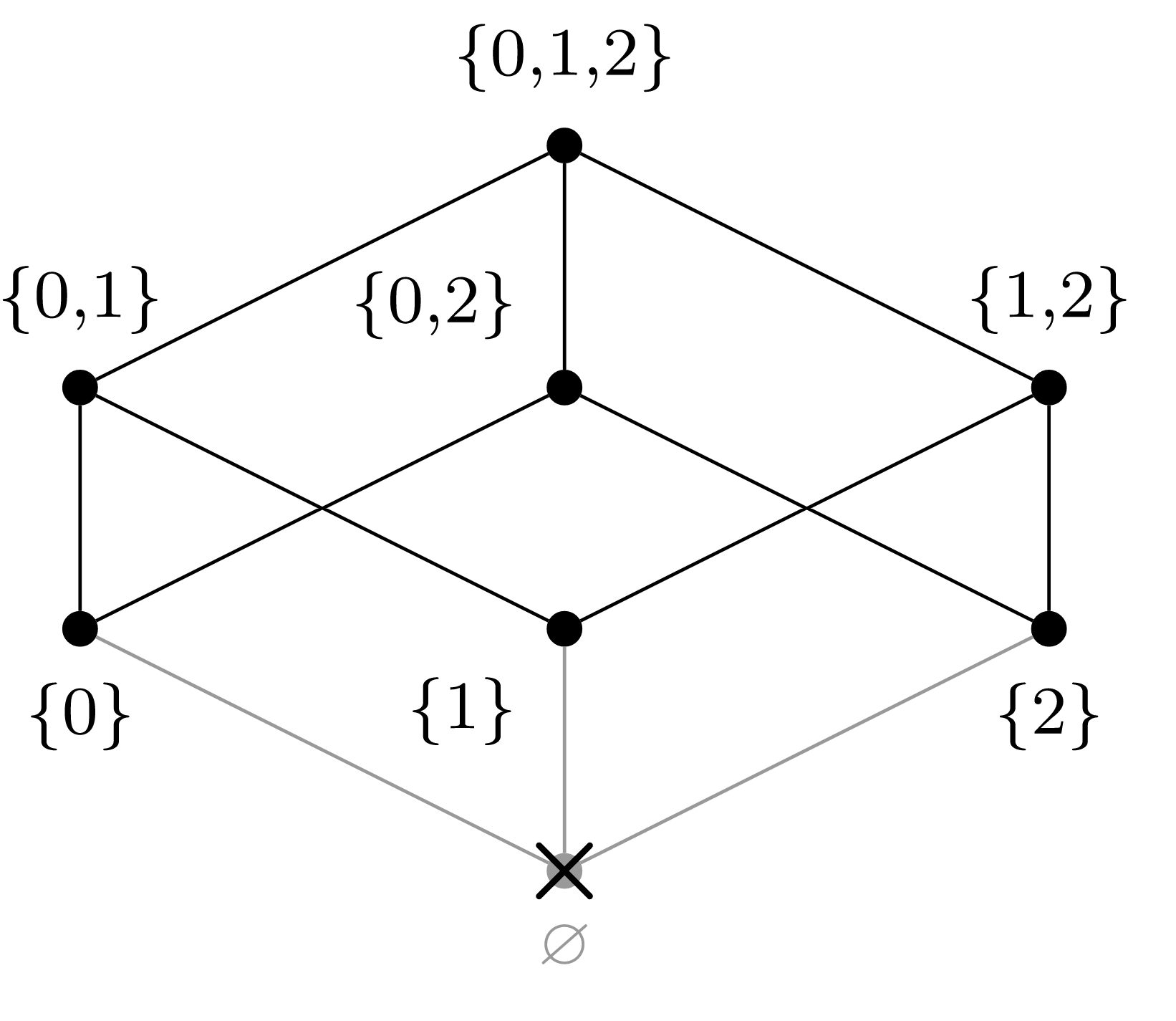
b) Elegir\(a_1 = \{2\}\text{.}\)
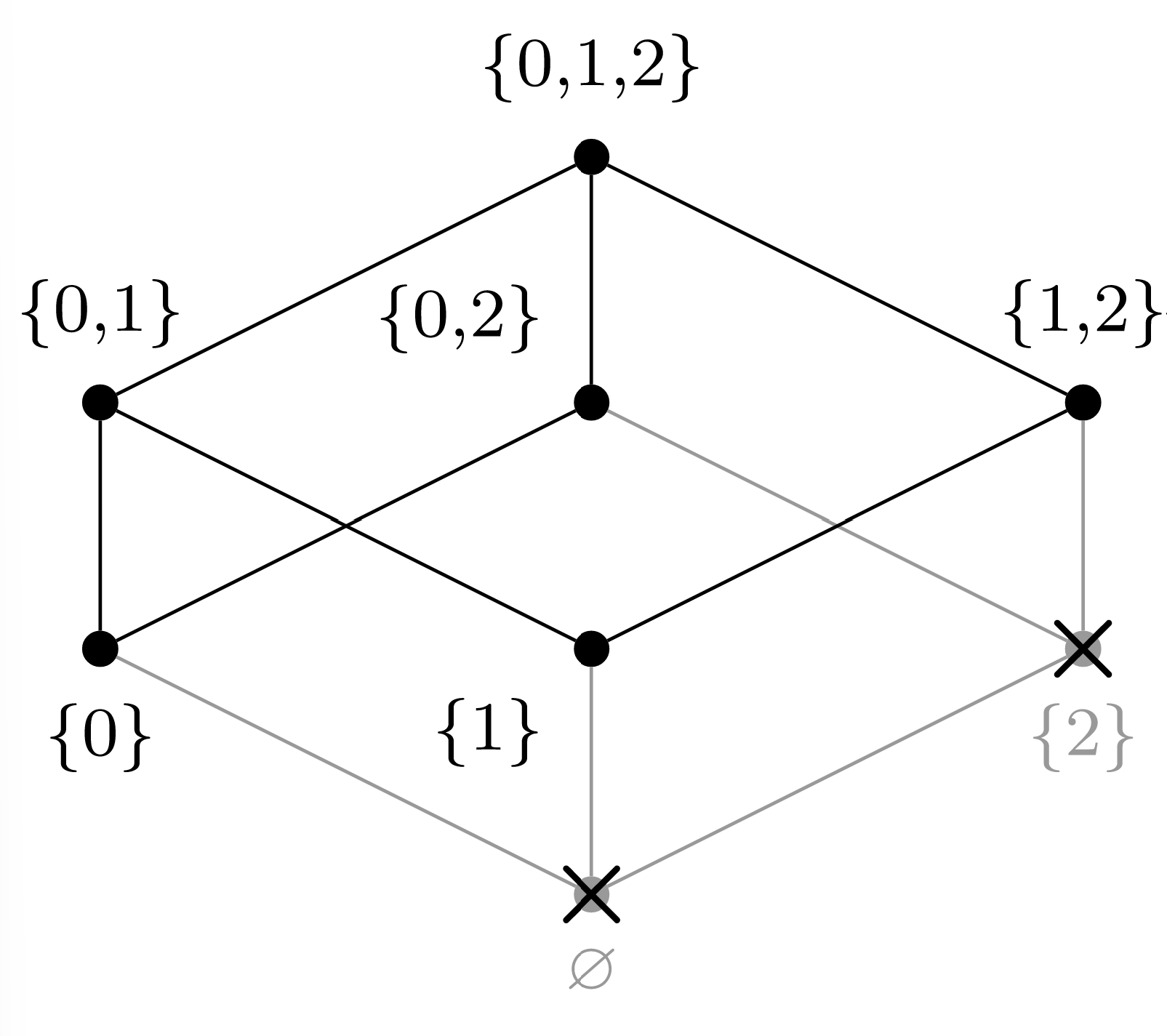
(c) Elegir\(a_2 = \{0\}\text{.}\)
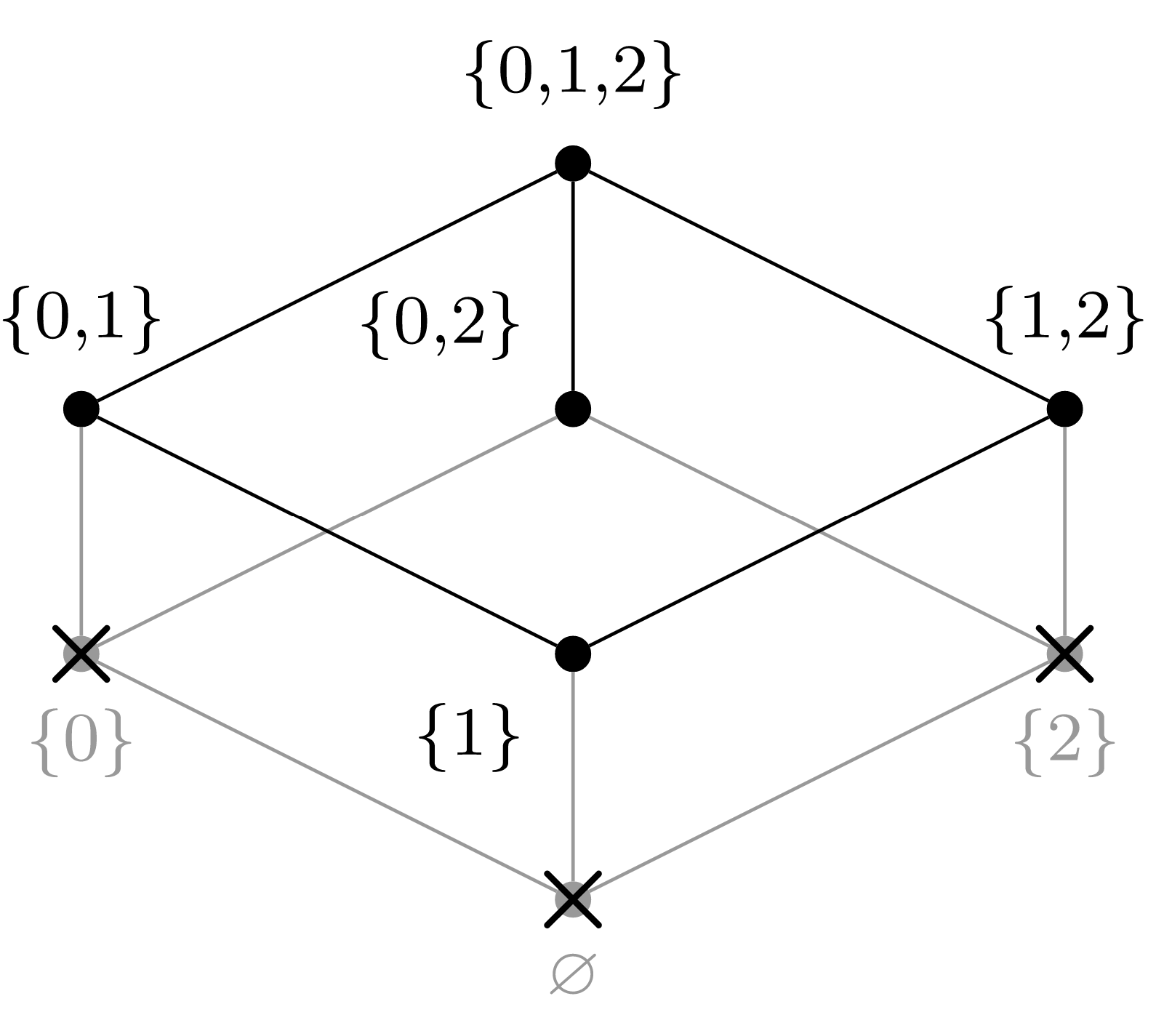
(d) Elegir\(a_3 = \{0,2\}\text{.}\)
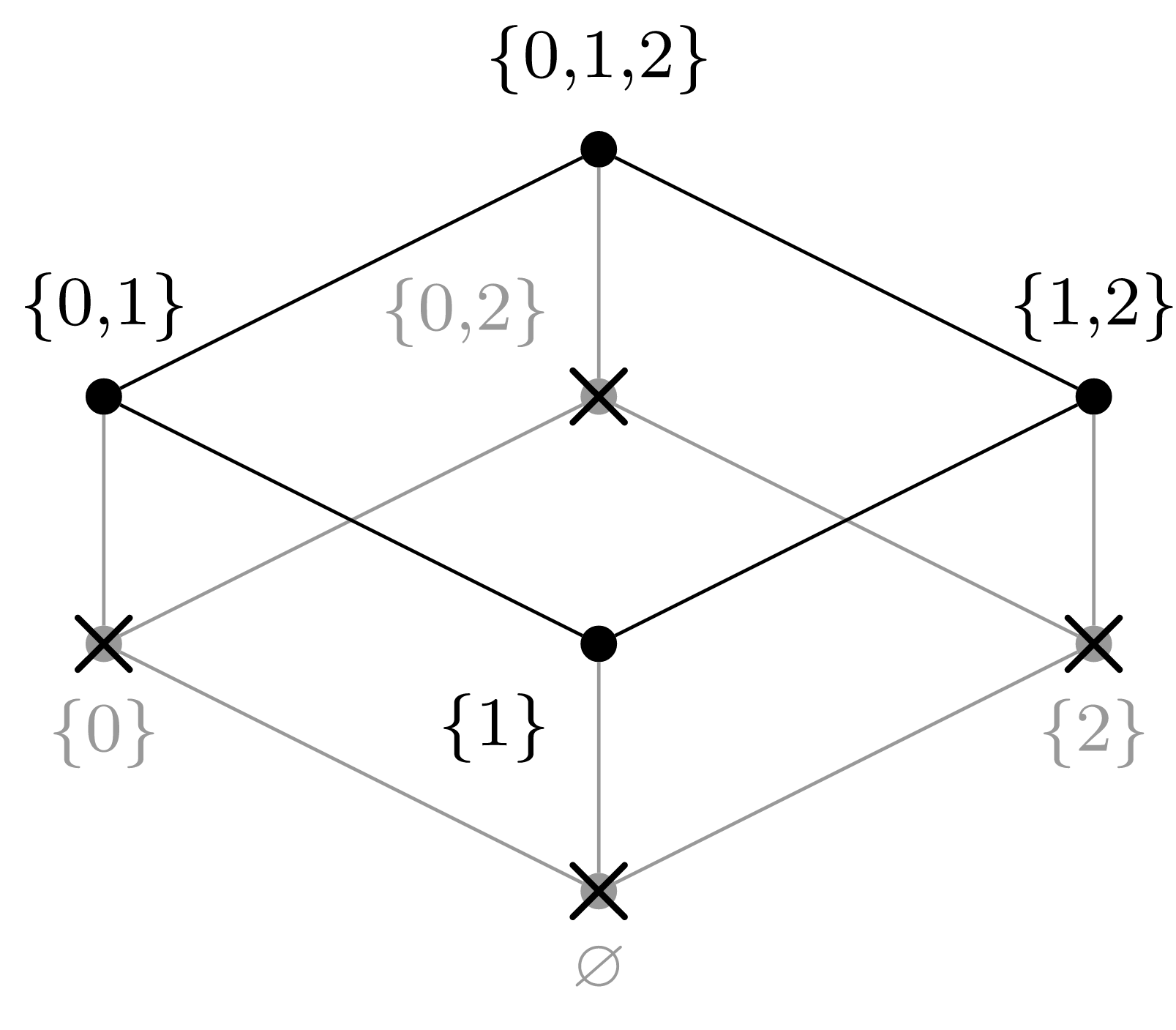
(e) Elegir\(a_4 = \{1\}\text{.}\)
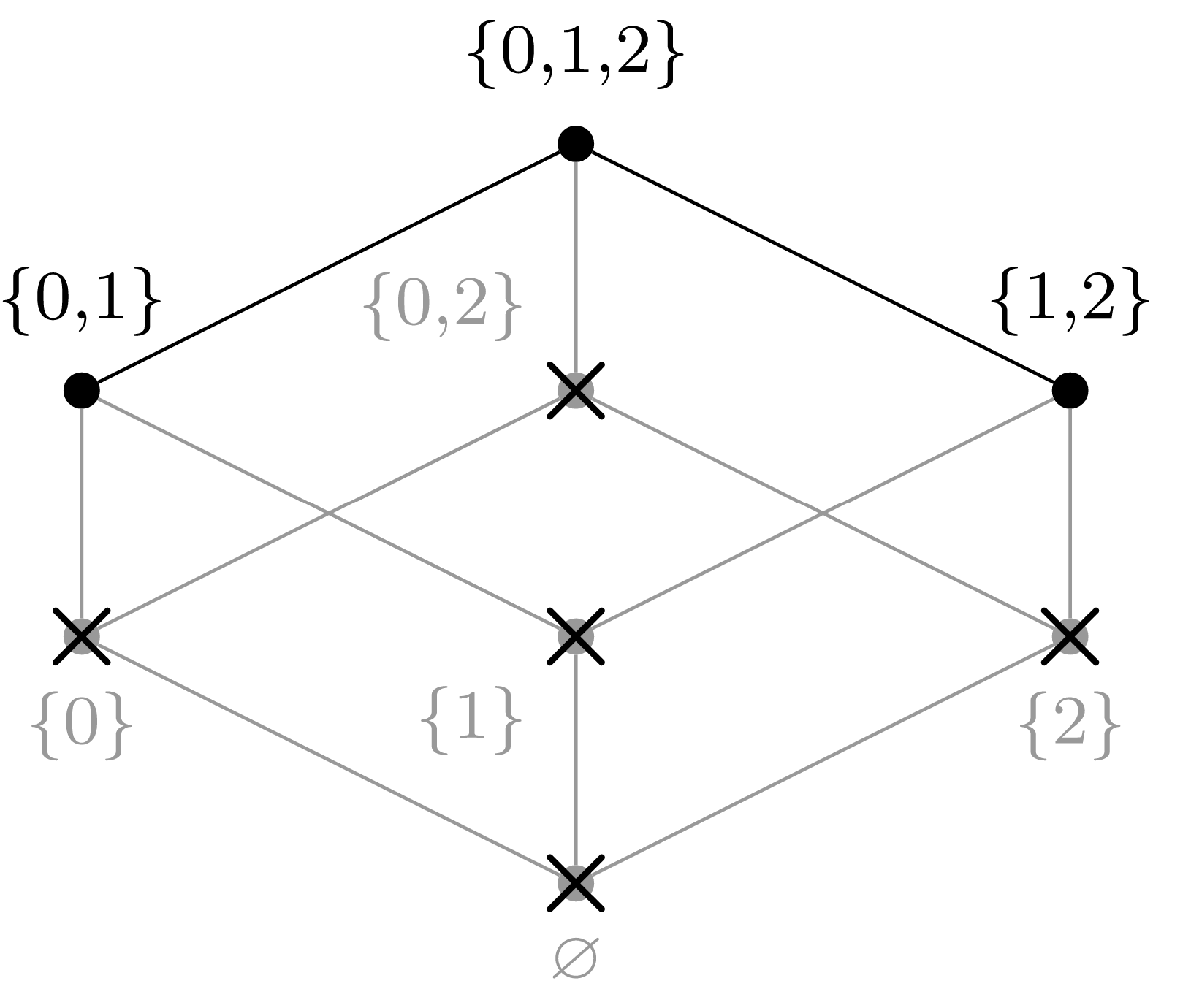
(f) Elegir\(a_5 = \{1,2\}\text{.}\)
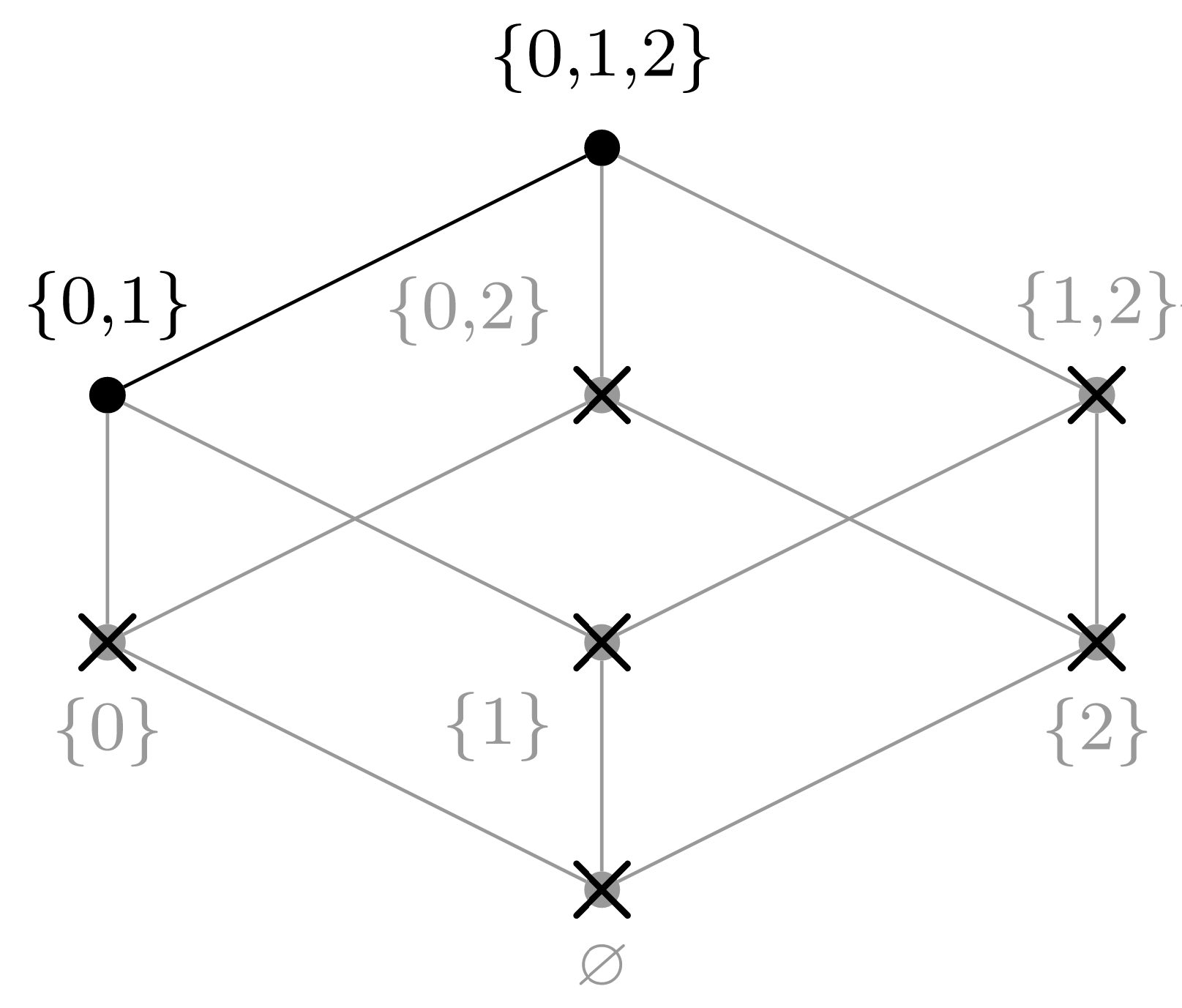
(g) Elegir\(a_6 = \{0,1\}\text{.}\)
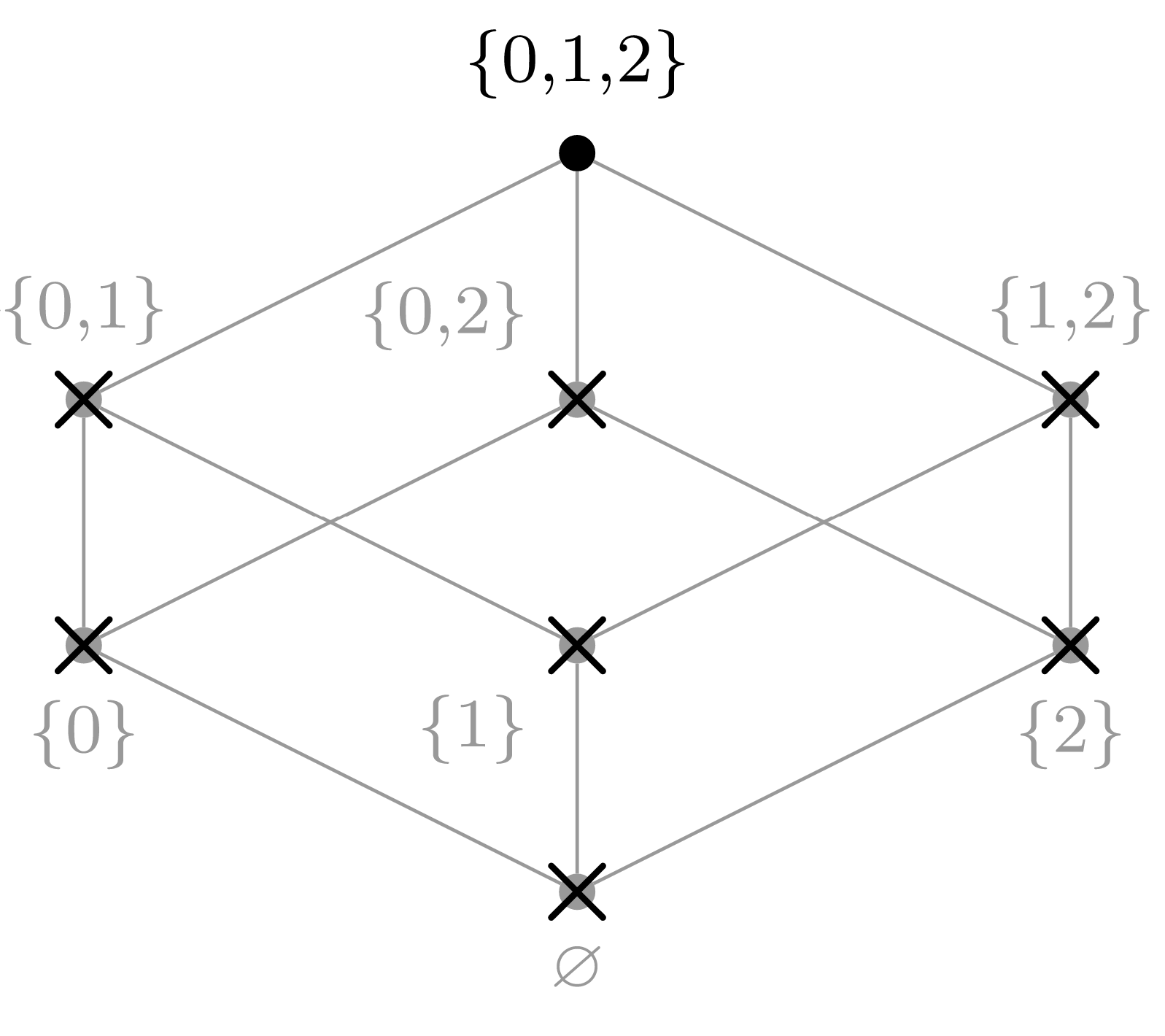
(h) Elegir\(a_7 = \{0,1,2\}\text{.}\)
Figura\(\PageIndex{1}\): Pegar subtítulo aquí
Nuestro resultado final es una lista de nuestras opciones, con el fin de:
Observe que el elemento máximo de\(A\) terminó en la “parte superior” del orden total y el elemento mínimo se vio obligado a la “parte inferior”.
Los pedidos totales compatibles no son únicos: en el ejemplo trabajado anterior, el orden en el que se\(A\) escribieron originalmente los elementos de representa otro orden total compatible:
\ begin {ecuación*}\ juego vacío\ leq\ {0\}\ leq\ {1\}\ leq\ {2\}\ leq\ {0,1\}\ leq\ {0,2\}\ leq\ {1,2\}\ leq\ {0,1,2\}\ texto {.} \ end {ecuación*}


