21.4: Permutaciones de Subconjuntos

A veces queremos crear una lista ordenada de cierta longitud a partir de un grupo más grande de candidatos.

Definición: Permutación de tamaño\(k\)

una lista ordenada de\(k\) elementos de un conjunto dado\(A\text{,}\) con\(\vert A \vert \ge k\)

Definición:\(P(n, k)\)

el número de permutaciones de tamaño\(k\) tomadas de un conjunto de tamaños\(n\)

Definición:\(P^n_k\text{,}\) \(_nP_k\)

opciones alternativas de notación para\(P(n, k)\)

Ejemplo\(\PageIndex{1}\): Visualizing \(P(4, 2)\).

Considera\(A = \{1,2,3,4\}\text{,}\) para que\(n = \vert A \vert = 4\text{.}\) haya\(4! = 24 \) permutaciones de\(A\text{.}\)

Figura\(\PageIndex{1}\): Permutaciones de un conjunto de tamaños\(4\text{.}\)

Observe que las permutaciones anteriores se han agrupado en pares, donde las dos permutaciones en un par dado tienen los mismos dos primeros elementos en el mismo orden. De esto, podemos concluir que solo hay\(24/2 = 12\) permutaciones de tamaño\(k=2\) a partir de\(A\text{.}\)

Teorema\(\PageIndex{1}\): Computing \(P(n, k)\).

Tenemos

\ comenzar {ecuación*} P (n, k) =\ dfrac {n!} {(n-k)!} = n (n-1) (n-2)\ cdots (n-k+1)\ texto {.} \ end {ecuación*}

Prueba.

Una forma de construir una lista ordenada de\(k\) elementos a partir de un conjunto\(A\text{,}\) donde\(\vert A \vert = n\text{,}\) es como en Ejemplo\(\PageIndex{1}\). Formar una lista ordenada de todos los elementos de\(A\) (\(n!\)vías), y luego tomar los primeros\(k\) elementos de esa lista. Pero obtenemos la misma lista ordenada de longitud\(k\) sin importar cómo se ordenen los últimos\(n-k\) elementos. Es decir, consideramos que dos ordenamientos cualesquiera de todos los\(n\) elementos son equivalentes si los primeros\(k\) elementos de la lista son los mismos entre los dos. Como hay\((n-k)!\) diferentes formas de ordenar los últimos\(n - k\) elementos manteniendo los primeros\(k\) elementos iguales, cada clase de equivalencia tiene tamaño\((n - k)!\text{.}\) Aplicando la Regla de División, obtenemos la fórmula deseada

\ begin {ecuación*} P (n, k) =\ dfrac {\ #\ {\ texto {ordenamientos de todos} n\ texto {elementos}\}} {\ #\ {\ texto {reordenamientos de los últimos} n - k\ texto {elementos}\}} =\ dfrac {n!} {(n - k)!} \ texto {.} \ end {ecuación*}

Comentario\(\PageIndex{1}\)

El número\(P(n,n)\) representa el número de formas de construir una lista ordenada de\(n\) elementos elegidos de un conjunto de\(n\) elementos, por lo que\(P(n,n) = n!\text{.}\) La convención\(0! = 1\) asegura que nuestra fórmula para\(P(n,k)\) expresado en Teorema\(\PageIndex{1}\) sigue siendo válida en el caso\(k = n\text{.}\)

Ejemplo\(\PageIndex{2}\): Elections.

Una clase de veinte estudiantes discretos de matemáticas decide elegir un presidente y vicepresidente de clase. ¿Cuántos resultados posibles para el proceso electoral hay?

Solución

Una manera arbitraria de elegir a los estudiantes para estos cargos sería alinear a todos los estudiantes y elegir a los dos primeros estudiantes en fila para ser presidente y vicepresidente, respectivamente. Por lo tanto, hay

\ begin {ecuación*} P (20, 2) =\ dfrac {20!} {(20 - 2)!} = 20\ cdot 19 = 380\ end {ecuación*}
posibles resultados a la elección.

Ejemplo\(\PageIndex{3}\): Ranking choices.

Se va a la pista de caballos para apostar en una carrera. De un campo de nueve caballos, ¿cuántas formas hay de hacer una apuesta “Trifecta” (es decir, especificar los tres primeros finalistas en orden)?

Solución

Hay

\ begin {ecuación*} P (9, 3) =\ dfrac {9!} {(9 - 3)!} = 9\ cdot 8\ cdot 7 = 504\ end {ecuación*}
posibles tales apuestas.

Ejemplo\(\PageIndex{4}\): Words with no repeated letters.

Para el alfabeto\(\Sigma = \{a, b, c, \ldots, y, z\}\text{,}\) cuántas palabras de cuatro letras compuestas por letras distintas hay en\(\Sigma^{\ast}\text{?}\)

Comparar.

Ver Ejemplo Trabajado 20.3.6.

Solución

Una palabra de cuatro letras sin letras repetidas es lo mismo que una permutación de tamaño\(4\text{,}\) por lo que el número de tales palabras es

\ begin {ecuación*} P (26, 4) =\ dfrac {26!} {(26 - 4)!} = 26\ cdot 25\ cdot 24\ cdot 23 = 358.800\ texto {.} \ end {ecuación*}

Ejemplo\(\PageIndex{5}\)

¿Si\(\vert A \vert = k\) y\(\vert B \vert = n\text{,}\) con\(k \le n\text{,}\) cuántas funciones inyectoras\(f: A \rightarrow B\) existen?

Comparar.

Ver Ejemplo Trabajado 20.3.9.

Solución

Arreglar un orden\(a_1,a_2,\ldots,a_k\) de los elementos de\(A\text{.}\) Entonces de cualquier orden\(b_1, b_2, \ldots, b_k\)\(k\) de tamaño de\(B\text{,}\) obtenemos una función de inyección\(f: A \hookrightarrow B\) por la siguiente tabla de valores.

Figura\(\PageIndex{2}\)

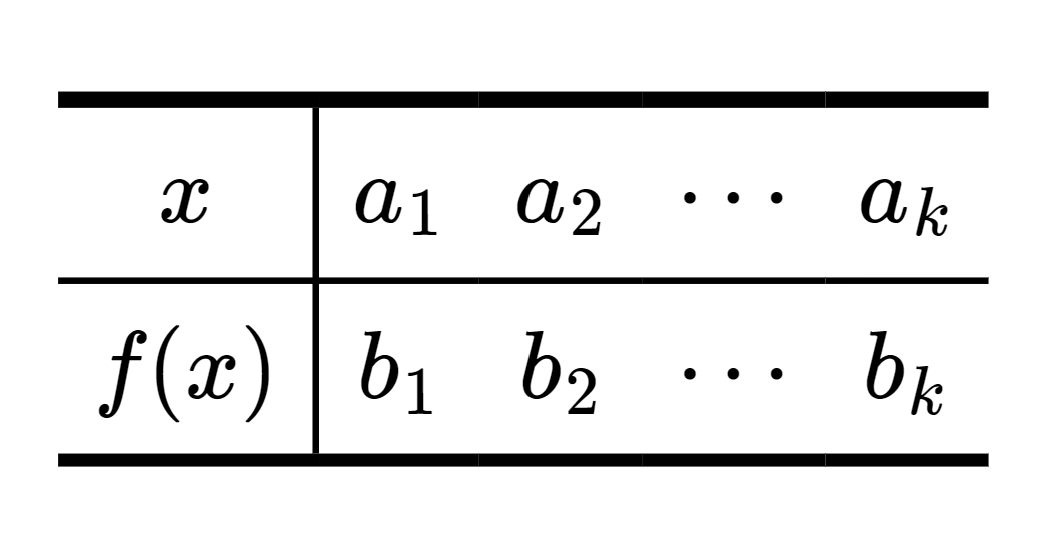
Es decir, cada permutación\(B\) de tamaño\(k\) corresponde a una inyección\(f: A \hookrightarrow B \text{,}\) y así el número de tales inyecciones es\(P(n, k)\text{.}\)