22.4: Propiedades
- Page ID
- 118433
Nota: En esta sección utilizaremos la notación alternativa\(C^n_k\) en lugar de\(C(n, k). \)
Los valores de combinación a\(C^n_k\) medida que variamos\(n\) y\(k\) exhibimos algunos patrones — ver Figura\(\PageIndex{1}\) abajo.
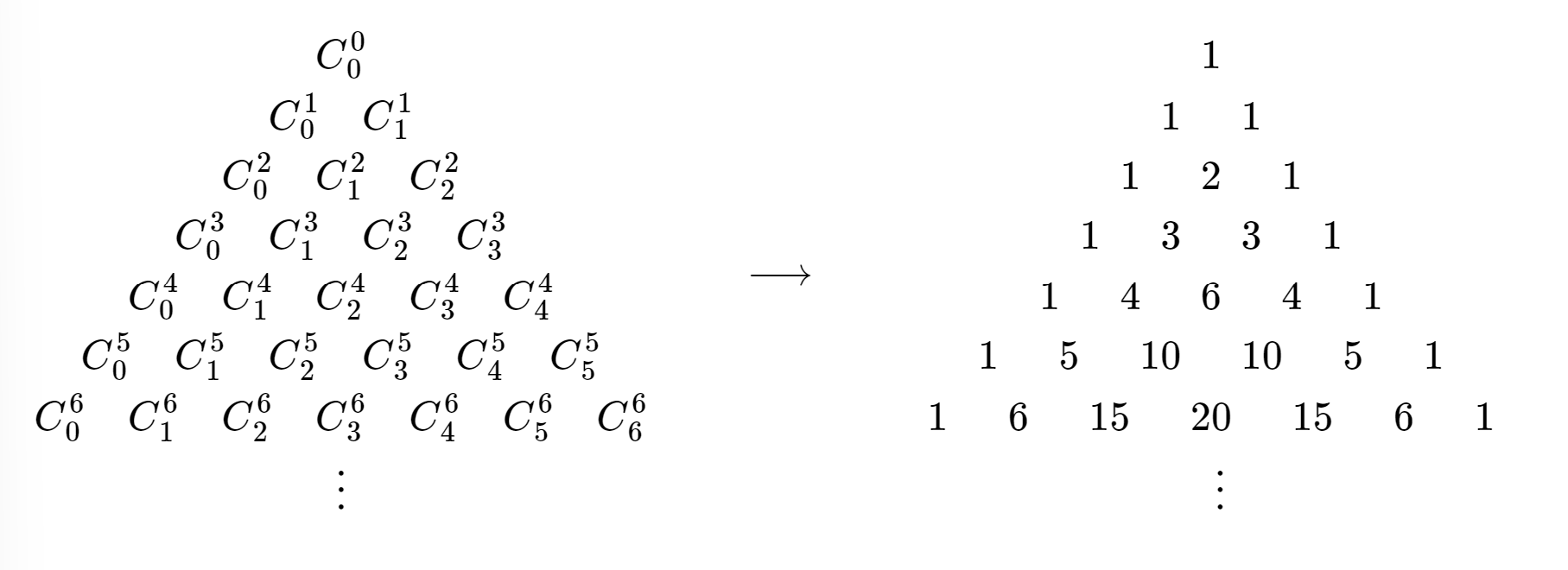
Al estudiar la versión del triángulo de Pascal que involucra los valores de combinación reales, estos son algunos de los patrones que observamos.
- Los valores son simétricos alrededor de una línea vertical a través del centro del triángulo.
- Parece que cada entrada es la suma de las dos entradas inmediatamente arriba.
- Parece que cada fila suma a un poder de\(2\text{.}\)
Ya hemos observado que el primer patrón surge de la equivalencia de elegir versus rechazar elementos para formar un subconjunto (ver Corolario 22.2.1 y Observación 22.2.1).
Las dos proposiciones siguientes confirman que los otros dos patrones observados continúan a lo largo del triángulo.
Para\(n \ge 2\) y\(1\le k \le n-1\text{,}\) tenemos\(C^n_k = C^{n-1}_{k-1} + C^{n-1}_{k} \text{.}\)
- Contestar
-
Podríamos probar esta igualdad con sólo comparar las fórmulas factoriales involucradas en los lados izquierdo y derecho. Pero en cambio consideraremos cada uno de estos valores de combinación como representando el número de subconjuntos de cierto tamaño.
Escribir
\ begin {ecuación*} A =\ mathbb {N} _ {<n} =\ {0,1,2,\ ldots, n - 1\}\ end {ecuación*}
para que\(\vert A \vert = n\text{.}\) Entonces el lado izquierdo de la igualdad en la declaración de la proposición represente el número de subconjuntos\(A\) de tamaño\(k\text{.}\) Vamos a romper esa colección de subconjuntos en dos subcolecciones.Subconjuntos\(A\) de tamaño\(k\) que contienen\(0\).
Cada uno de estos subconjuntos constará\(0\) junto con elementos\(k - 1\) distintos de cero. Como\(A\) contiene elementos\(n - 1\) distintos de cero entre los que elegir, hay\(C^{n-1}_{k-1}\) formas de seleccionar esos elementos de subconjunto adicionales de\(A\text{.}\)Subconjuntos\(A\) de tamaño\(k\) que no contienen\(0\).
Cada uno de estos subconjuntos debe constar de elementos\(k\) distintos de cero. Como\(A\) contiene elementos\(n - 1\) distintos de cero entre los que elegir, hay\(C^{n-1}_{k}\) formas de seleccionar esos elementos de subconjunto de\(A\text{.}\)Al sumar estos dos casos disjuntos usando la Regla de Adición se obtiene el lado derecho de la igualdad.
Para\(n\ge 0\text{,}\) nosotros tenemos\(\displaystyle \sum_{k=0}^n C^n_k = 2^n\text{.}\)
- Comprobante.
-
Primero, recordemos que la notación en el lado izquierdo es notación de suma:
\ begin {ecuación*}\ suma_ {k=0} ^n C^n_k = C^ {n} _ {0} + C^ {n} _ {1} +\ cdots + C^ {n} _ {n}\ texto {.} \ end {equation*}
Dejar\(A = \mathbb{N}_{<n}\text{,}\) así que\(\vert A \vert = n\text{.}\) Entonces\(\vert \mathscr{P}(A) \vert = 2^n\) (Teorema 12.2.9). Entonces, el lado derecho de la igualdad representa el número de posibles subconjuntos de\(A\text{.}\)Por otro lado, para cada índice\(k\) en la suma del lado izquierdo, el término\(C^n_k\) es el número de subconjuntos de tamaño\(k\text{.}\) Usando la Regla\(A\) de Adición, la suma de estos términos también debe ser el número total de subconjuntos posibles de\(A\text{.}\)
Aquí hay otra propiedad de la función choose.
Para\(0 \le m \le n\text{,}\) nosotros tenemos
\ begin {ecuación*} C^ {n+1} _ {m+1} =\ suma_ {k=m} ^n C^ {k} _ _ {m}\ texto {.} \ end {ecuación*}
- Comprobante.
-
Supongamos que\(A\) es un conjunto finito con\(\vert A \vert = n + 1\text{.}\) (Por ejemplo, podríamos usar\(A = \mathbb{N}_{<n+1}\text{,}\) pero eso podría resultar confuso entre números como elementos de\(A\) y números como cardinalidades de subconjuntos de\(A\text{.}\)) Entonces el lado izquierdo de la igualdad es el número de subconjuntos de\(A\) de tamaño \(m + 1\text{.}\)Aquí hay una manera sistemática que podríamos crear esos subconjuntos.
Elija un orden de los elementos de\(A\text{,}\) para que
\ begin {ecuación*} A =\ {a_1, a_2,\ ldots, a_ {n+1}\}\ text {,}\ end {ecuación*}
aunque no contaremos esta elección de pedido. Después, proceda de la siguiente manera.- Escribir
\ begin {ecuación*} B_1 =\ {a_1, a_2,\ ldots, a_ {m+1}\}\ text {,}\ end {ecuación*}
para que\(B_1 \subseteq A\) con\(\vert B_1 \vert = m + 1\text{.}\) Entonces haya exactamente\(1 = C^{m+1}_{m+1}\) subconjunto\(B_1\) de tamaño\(m + 1\text{,}\) que es\(B_1\) en sí mismo. Y este subconjunto de\(B_1\) es también un subconjunto de\(A\text{.}\)- Escribir
\ begin {ecuation*} B_2 =\ {a_1, a_2,\ ldots, a_ {m+1}, a_ {m+2}\}\ text {,}\ end {equation*} de
manera que\(B_1 \subseteq B_2 \subseteq A\) con\(\vert B_2 \vert = m + 2\text{.}\) Usando solo los elementos de\(B_2\text{,}\) para crear un nuevo subconjunto\(X \subseteq A\) de tamaño\(m + 1\) que no hayamos contado ya debemos incluir el nuevo elemento\(a_{m+2}\text{,}\) con los\(m\) elementos restantes para componer\(X\) elegidos de\(B_1\text{.}\) Así que obtenemos\(C^{m+1}_{m}\) nuevos subconjuntos\(A\) de tamaño\(m+1\) de\(B_2\text{.}\)- Escribir
\ begin {ecuación*} B_3 =\ {a_1, a_2,\ ldots, a_ {m+1}, a_ {m+2}, a_ {m+3}\}\ text {,}\ end {ecuación*} de
manera que\(B_2 \subseteq B_3 \subseteq A\) con\(\vert B_3 \vert = m + 3\text{.}\) Usando solo los elementos de\(B_3\text{,}\) para crear un nuevo subconjunto\(X \subseteq A\) de tamaño\(m + 1\) que aún no hayamos contado debemos incluir el nuevo elemento \(a_{m+3}\text{,}\)con los\(m\) elementos restantes para componer\(X\) elegidos de\(B_2\text{.}\) Así que obtenemos\(C^{m+2}_{m}\) nuevos subconjuntos\(A\) de tamaño\(m+1\) de\(B_3\text{.}\)Y así sucesivamente. El último paso en este proceso es cuando creamos nuevos subconjuntos de tamaño\(m+1\) eligiendo primero incluir\(a_{n+1}\text{,}\) y luego eligiendo los\(m\) elementos restantes de\(A \smallsetminus \{a_{n+1}\}\text{,}\) darnos\(C^{n}_{m}\) nuevos subconjuntos.
Cada subconjunto\(X \subseteq A\) de tamaño\(m + 1\) se contabiliza en el proceso anterior, ya que cada subconjunto de este tipo debe contener al menos un elemento con índice\(m + 1\) o mayor. Si\(a_N\) es el elemento\(X\) con el índice más grande, entonces\(X\) es uno de los subconjuntos considerados en el paso\(\ell\text{,}\) donde\(N = m + \ell\text{.}\)
Por lo que sumar cada uno de estos casos disjuntos usando la Regla de Adición debe arrojar el número total de subconjuntos\(A\) de tamaño\(m + 1\text{.}\) Sustituyendo el\(C^{m+1}_{m+1}\) total desde el primer paso con\(C^{m}_{m}\) (ya que ambos son iguales a\(1\)) para que coincidan con el patrón de los pasos posteriores, nosotros obtener
\ begin {ecuación*} C^ {n+1} _ {m+1} = C^ {m} _ {m} + C^ {m+1} _ {m} +\ cdots + C^ {n} _ {m}\ text {,}\ end {ecuación*}
como se desee.


