Saltar al contenido principal
LibreTexts Español

22.5: Actividades

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    118444

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Actividad\(\PageIndex{1}\)

    De un grupo de once estudiantes (cinco de primer año, seis de último año), cuántas formas hay de formar:

    1. ¿Un comité de tres alumnos?
    2. ¿Un comité integrado por tres estudiantes de primer año y cuatro estudiantes de último año?
    3. ¿Un comité de seis estudiantes si dos de los estudiantes de último año se niegan a estar juntos en el comité?
    4. ¿Un comité integrado por cuatro estudiantes de primer año y tres estudiantes de último año si dos de los estudiantes de primer año se niegan a estar juntos en el equipo?

    Actividad\(\PageIndex{2}\)

    Del alfabeto\(\Sigma = \{0,1\}\text{:}\)

    1. ¿Cuántas palabras de longitud\(10\) contienen exactamente seis\(0\) s?
    2. ¿Cuántos contienen al menos tres\(1\) s?

    Actividad\(\PageIndex{3}\)

    Del alfabeto\(\Sigma = \{0,1,2\}\text{:}\)

    1. ¿Cuántas palabras de longitud\(10\) contienen exactamente cuatro\(2\) s?
    2. ¿Cuántos contienen como máximo siete\(0\) s?

    Actividad\(\PageIndex{4}\)

    La figura\(\PageIndex{1}\) contiene un diagrama en forma de pirámide. Los círculos sin rellenar representan “posiciones” en la pirámide, y los puntos más pequeños representan “divisores” entre posiciones. Considera “caminos” a través de esta pirámide que comienzan en la posición de pico y terminan en el nivel más bajo. Los círculos rellenos unidos por segmentos de línea representan uno de esos caminos.

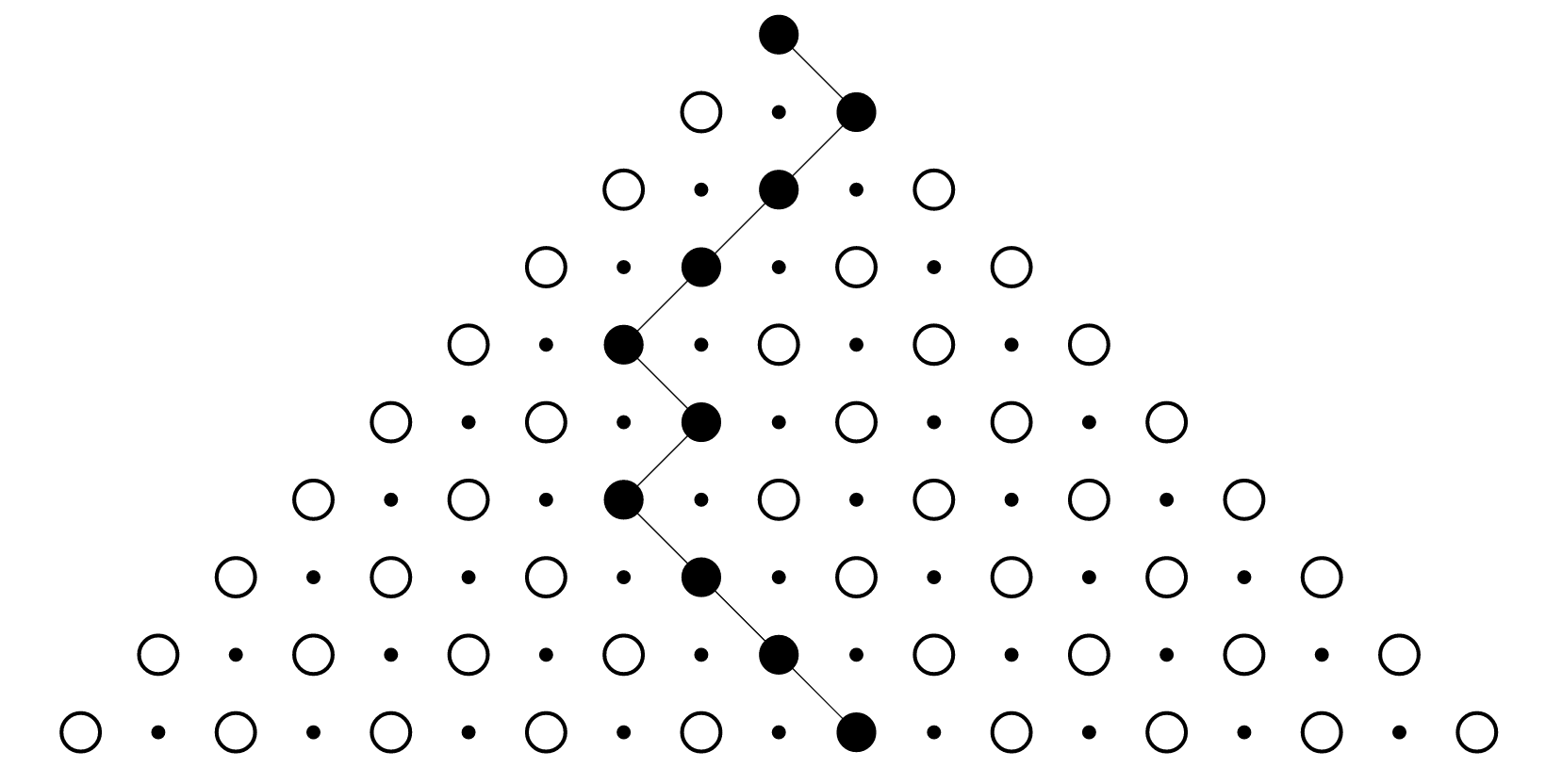
    clipboard_e207b9b3990cdbc303e3a75772ff3630a.png
    Figura\(\PageIndex{1}\): Pirámide estilo CA Plinko™.
    1. ¿Cuántos caminos de este tipo hay?
    2. ¿Cuántos caminos hay que cambian de dirección exactamente una vez? Exactamente dos veces? ¿A cada paso?

    (Para cada caso descrito en esta tarea, debería poder llegar a una respuesta sin determinar explícitamente todas esas rutas).

    Actividad\(\PageIndex{5}\)

    Llegas al examen final de uno de tus cursos y te enfrentas a doce preguntas. De cuantas formas puedes cumplir con el examen de requisitos si las instrucciones te piden:

    1. ¿Contesta alguna diez de las preguntas?
    2. ¿Contesta siete de las ocho primeras preguntas y tres cualesquiera de las últimas cuatro preguntas?
    3. Contestar diez de las preguntas, ¿al menos cinco de las cuales deben ser de las ocho primeras preguntas y al menos tres de las cuales deben ser de las últimas cuatro preguntas?

    Actividad\(\PageIndex{6}\)

    Un instructor de curso para una clase de veinte se siente particularmente perezoso y no se molesta en marcar los exámenes finales. En cambio, decide que por cada una de las calificaciones de letras A, B, C, asignará esa calificación aleatoriamente a exactamente seis estudiantes, y a los dos últimos estudiantes desafortunados se les asignará una calificación de D. ¿Cuántos resultados diferentes del curso hay?

    Actividad\(\PageIndex{7}\)

    ¿Cuántas formas hay de dividir a\(m n \) las personas en\(m\) grupos de igual tamaño?

    Actividad\(\PageIndex{8}\)

    Supongamos que tienes\(2 n\) ositos de peluche que son idénticos a excepción de un número cosido en la pata del pie derecho. De estos osos,\(n\) tienen el número\(0\) en su pie, y los\(n\) osos restantes tienen un número único de\(1, 2, 3, \ldots, n\text{.}\) ¿Cuántas formas puedes elegir\(n\) de los osos, entendiendo que alguno de los\(0\) osos etiquetados es intercambiable?

    Insinuación.

    Dividir en cajas en función de cuántos osos etiquetados\(0\) habrá en tu colección.

    Actividad\(\PageIndex{9}\)

    Considera el conjunto\(\{ 1, 2, 3, \ldots, 2n \}\text{.}\) ¿Cuántos subconjuntos de tamaño\(2\) hay tal que los dos elementos en el mismo tengan una suma par?

    Actividad\(\PageIndex{1}\)

    Considera el conjunto\(\{ 1, 2, 3, \ldots, n \}\text{.}\) ¿Cuántos subconjuntos de tamaño\(3\) hay tal que no sean consecutivos dos de los tres elementos en el mismo?

    Insinuación.

    Podría ser más fácil contar los subconjuntos de tamaño\(3\) que contienen (al menos) dos números consecutivos.

     

    This page titled 22.5: Actividades is shared under a GNU Free Documentation License 1.3 license and was authored, remixed, and/or curated by Jeremy Sylvestre via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.