23.1: Coeficientes bionomiales
- Page ID
- 118341
una expresión de la forma\((x + y)^n\text{,}\) donde\(n \in \mathbb{N}\) y\(x,y\) son números reales (o elementos de cualquier anillo conmutativo con identidad)
La expansión de binomios se complica más a medida que\(n\) aumenta.
\ begin {alinear*} (x + y) ^2 & = x^2 + 2 x y + y^2\\ (x + y) ^3 & = (x + y) (x^2 + 2 x y + y^2) = x^3 + 3 x^2 y + 3 x y^2 + y^3\\ (x + y) ^4 & = (x + y) (x^^3 + 3 x^2 y + 3 x y^2 + y^3) = x^4 + 4 x^3 y + 6 x^2 y^2 + 4 x y^3 + y^4\\ (x + y) ^5 & = (x + y) (x^4 + 4 x^3 y + 6 x^2 y^2 + 4 x y^3 + y^4)\ & amp; = x^5 + 5 x^4 y + 10 x^3 y^2 + 10 x^2 y^3 + 5 x y^4 + y^5\\ &\ vdots\ end {align*}
La simetría en cada una de estas expansiones debería esperarse: obtendríamos la misma expresión en el orden opuesto de suma si cambiáramos\(x\) y\(y\text{,}\) desde\((x + y)^n = (y + x)^n\text{.}\)
un número que aparece como coeficiente en la expansión de\((x + y)^n\)
el\(k^{th}\) coeficiente en la expansión de\((x + y)^n\) (\(0 \le k \le n\))
Para comprender mejor la complejidad de las expansiones binomiales, debemos buscar y explotar patrones. Ya hemos expandido algunas expresiones binomiales para pequeños exponentes en Ejemplo\(\PageIndex{1}\) — vamos a extraer los coeficientes binomiales de esas expresiones.
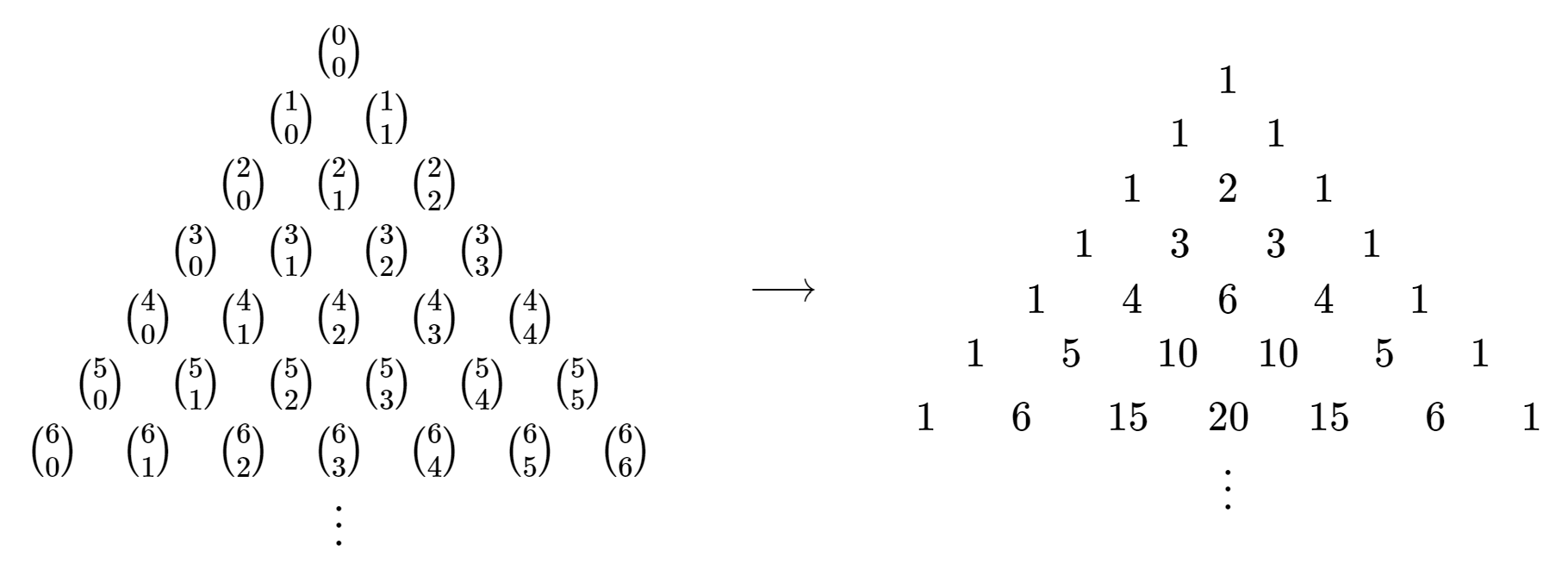
La figura\(\PageIndex{1}\) anterior seguro se parece mucho a la Figura 22.4.1.
Para todos\(x,y\in\mathbb{R}\) y cada uno de los\(n \in \mathbb{N}\text{,}\) que tenemos
\ begin {ecuación*} (x+y) ^n =\ suma_ {k=0} ^n\ binom {n} {k}\, x^ {n-k} y^k =\ binom {n} {0}\, x^n +\ binom {n} {1}\, x^ {n-1} y +\ binom {n} {2}\, x^ {n-2} y^2 +\ cdots +\ binom {n} {n-1}\, xy^ {n-1} +\ binom {n} {n}\, y^n,\ end {ecuación*}
donde
\ comenzar {ecuación*}\ binom {n} {k} = C^n_k =\ dfrac {n!} {k! (n-k)!} \ texto {.} \ end {ecuación*}
- Esquema de prueba directa informal.
-
Escribir\((x+y)^n = (x+y)(x+y)\cdots(x+y)\text{,}\) con\(n\) factores. Para ampliar esto, generalizamos el método FOIL: de cada factor, elige uno\(x\) o\(y\text{,}\) luego multiplica todas tus elecciones juntas. Luego agregue los resultados de todos los posibles productos de este tipo. Por ejemplo,
\ begin {alinear*} (x + y) ^2 & = x x + y + y x y = x^2 + 2 x y + y^2,\\ (x + y) ^3 & = x x + x x y + x y + x y x y + y x y + y x y + y y x + y y x y = x^3 + 3 x^2y + y x y + y y = x^3 + 3 x^2y + y y^2 + y^3. \ end {align*}
Al formar un producto específico, si eliges\(y\)\(k\) fuera de\(n\) las opciones, debes haber elegido\(x\) para el resto\(n - k\) de las\(n\) opciones. El resultado será\(x^{n - k} y^k\text{.}\) Así para averiguar el coeficiente en\(x^{n - k} y^k\text{,}\) solo contar cuántas formas hay de elegir\(y\) para\(k\) de las\(n\) elecciones. Aquí es justo\(C^n_k\text{,}\) donde elegimos\(k\) factores de\((x+y)\) para darnos una\(y\text{,}\) y el resto para darnos una\(x\text{.}\)
- Esquema a prueba de inducción.
-
Estuche base.
Los casos de\(n=0,1\) son trivialmente ciertos.Paso de inducción.
Utilice la fórmula binomial\((x+y)^{n - 1}\) para obtener la fórmula binomial para\((x + y)^n\text{,}\) manipulando\ begin {alinear*} (x + y) ^n & = (x + y) (x + y) ^ {n - 1}\\ & = (x + y) (C^ {n-1} _0\, x^ {n - 1} + C^ {n-1} _1\, x^ {n - 2} y +\ cdots + C^ {n-1} _ {n-1}\, y^ {n - 1})\ text {.} \ end {alinear*}
Ampliar\((x-2)^5\text{.}\)
Solución
Vimos que la\(n = 5\) fila del triángulo de Pascal es\(1,5,10,10,5,1\text{.}\)
\ begin {alinear*} & (x - 2) ^5\\ & (x + (- 2)) ^5\\ & =\ binom {5} {0} x^5 +\ binom {5} {1} x^4 (-2) +\ binom {5} {2} x^3 (-2) ^2 +\ binom {5} {3} x^2 (-2) 3 +\ binom {5} {4} x (-2) ^4 +\ binom {5} {5} (-2) ^5\\ & = x^5 - 10 x^4 + 40 x^3 - 80 x^2 + 80 x - 32. \ end {alinear*}
¿Cuál es el coeficiente sobre el\(x^4 y^9\) término en la expansión de\((3 x + y)^{13} \text{?}\)
Solución
Considerando
\ begin {ecuación*} (3 x + y) ^ {13} = ((3 x) + y) ^ {13}\ text {,}\ end {ecuación*}
el\(x^4 y^9\) término es
\ begin {alinear*}\ binom {13} {9} (3x) ^4 y^9 & =\ dfrac {13!} {9! ¡4!} \ cdot 3^4 x^4 y^9\\ & =\ dfrac {13\ cdot 12\ cdot 11\ cdot 10\ cdot 27\ cdot 3} {4\ cdot 3\ cdot 2} x^4 y^9\ & = (13\ cdot 3\ cdot 11\ cdot 5\ cdot 27) x^4 y^9\ texto {.} \ end {align*}
Así que el coeficiente deseado es\(57,915\text{.}\)


