2.5: Equivalencias lógicas

Una tautología es una proposición que siempre es verdadera, independientemente de los valores de verdad de las variables proposicionales que contiene. Una proposición que siempre es falsa se llama contradicción. Una proposición que no es ni tautología ni contradicción se llama contingencia.

Ejemplo\(\PageIndex{1}\label{eg:logiceq-01}\)

De la siguiente tabla de la verdad\[\begin{array}{|c|c|c|c|} \hline p & \overline{p} & p \vee \overline{p} & p \wedge \overline{p} \\ \hline \text{T} & \text{F} & \text{T} & \text{F} \\ \text{F} & \text{T} & \text{T} & \text{F} \\ \hline \end{array} \nonumber\] recogemos que\(p\vee\overline{p}\) es una tautología, y\(p\wedge\overline{p}\) es una contradicción.

En palabras,\(p\vee\overline{p}\) dice que o la afirmación\(p\) es verdadera, o la afirmación\(\overline{p}\) es verdadera (es decir,\(p\) es falsa). Esta afirmación siempre es cierta.

El enunciado compuesto\(p\wedge\overline{p}\) afirma que\(p\) es cierto, y al mismo tiempo, también\(\overline{p}\) es cierto (lo que significa que\(p\) es falso). Esto es claramente imposible. De ahí,\(p\wedge \overline{p}\) debe ser falso.

Ejemplo\(\PageIndex{2}\label{eg:logiceq-02}\)

Demostrar que\((p \Rightarrow q) \Leftrightarrow (\overline{q} \Rightarrow \overline{p})\) es una tautología.

Contestar

Podemos usar una tabla de verdad para verificar la afirmación. \[\begin{array}{|*{7}{c|}} \hline p & q & p\Rightarrow q & \overline{q} & \overline{p} & \overline{q}\Rightarrow\overline{p} & (p \Rightarrow q) \Leftrightarrow (\overline{q} \Rightarrow \overline{p}) \\ \hline \text{T} & \text{T} & \text{T} & \text{T} & \text{F} & \text{F} & \text{T} \\ \text{F} & \text{T} & \text{T} & \text{F} & \text{T} & \text{T} & \text{T} \\ \text{F} & \text{F} & \text{T} & \text{T} & \text{T} & \text{T} & \text{T} \\ \hline \end{array} \nonumber\]Observe cómo trabajamos en cada componente de la declaración compuesta por separado antes de armarlos para obtener la respuesta final.

Ejemplo\(\PageIndex{3}\label{eg:logiceq-03}\)

Demostrar que el argumento

“Si\(p\) y\(q\), entonces\(r\). Por lo tanto, si no\(r\), entonces no\(p\) o no”\(q\).

es válido. Es decir, mostrar que la lógica utilizada en el argumento es correcta.

Contestar

Simbólicamente, el argumento dice\[[(p \wedge q) \Rightarrow r] \Rightarrow [\overline{r} \Rightarrow (\overline{p} \vee \overline{q})]. \label{eqn:tautology}\] Queremos demostrar que se trata de una tautología. Es fácil verificar con una tabla de verdad. También podemos argumentar que esta afirmación compuesta siempre es cierta al demostrar que nunca puede ser falsa.

Supongamos, por el contrario, que ([eqn:tautología]) es falso para algunas opciones de\(p\),\(q\), y\(r\). Entonces\[(p \wedge q) \Rightarrow r \quad \mbox{must be true}, \qquad\mbox{and}\qquad \overline{r} \Rightarrow (\overline{p} \vee \overline{q}) \quad \mbox{must be false}. \nonumber\] para que la segunda implicación sea falsa, necesitamos\[\overline{r} \quad\mbox{to be true}, \qquad\mbox{and}\qquad \overline{p} \vee \overline{q} \quad\mbox{to be false}. \nonumber\] Ellos a su vez implican que\(r\) es falso, y ambos\(\overline{p}\) y\(\overline{q}\) son falsos; de ahí ambos\(p\) y\(q\) son verdaderos. Esto haría\((p \wedge q) \Rightarrow r\) falso, contradiciendo la suposición de que es verdad. Así, ([eqn:tautología]) no puede ser falsa, debe ser una tautología.

ejercicio práctico\(\PageIndex{1}\label{he:logiceq-01}\)

Usa una tabla de verdad para mostrar que\[[(p \wedge q) \Rightarrow r] \Rightarrow [\overline{r} \Rightarrow (\overline{p} \vee \overline{q})] \nonumber\] es una tautología.

Contestar

Necesitamos ocho combinaciones de valores de verdad en\(p\),\(q\), y\(r\). Enumeramos los valores de la verdad de acuerdo a la siguiente convención. En la primera columna para los valores de verdad de\(p\), llenar la mitad superior con T y la mitad inferior con F. En la siguiente columna para los valores de verdad de\(q\), repita el mismo patrón, por separado, con la mitad superior y la mitad inferior. Entonces dividimos la mitad superior de la segunda columna en dos mitades, llenamos la mitad superior con T y la mitad inferior con F. Asimismo, dividimos la mitad inferior de la segunda columna en dos mitades, llenamos la mitad superior con T y la mitad inferior con F. Repetimos el mismo patrón con la tercera columna para los valores de verdad de \(r\), y así sucesivamente si tenemos más variables proposicionales.

Completa la siguiente tabla:\ [\ begin {array} {|* {11} {c|}}\ hline p & q & r & p\ wedge q & (p\ wedge q)\ Rightarrow r &\ overline {r} &\ overline {p} &\ overline {q} &\ overline {p}\ overline {p}\ vee\ overline {q} &\ overline {r}\ Derecha (\ overline {p}\ vee\ overline {q}) & [(p\ wedge q) \ Rightarrow r]\ Rightarrow [\ overline {r}\ Rightarrow (\ overline {p}\ vee\ overline {q})]\\\ hline\ text {T} &\ text {T} &\ text {T} &&&&&&&&&&\\ text {T} &\ text {T} &\ text {F} &&&&&&&&&&&&texto &&\\\ texto {T} &\ texto {F} &\ texto {T} &&& ; &&&&&\\\ text {T} &\ text {F} &\ text {F} &&&&&&&&&&\\ text {F} &\ text {T} &\ text {T} &&&&&&&&&\\ text {F} &\ text {T} &\ text {F} &&&&&&&&&\\ text {F} &\ texto {F} &\ texto {T} &&&&&&&&&\\\ text {F} &\ text {F} &\ text {F} &&&&&&&&&&\\ hline\ end {array}\\ nonumber] Pregunta: Si hay cuatro variables proposicionales en una proposición, ¿cuántas filas hay en la tabla de verdad?

Definición

Dos fórmulas lógicas\(p\) y\(q\) se dice que son lógicamente equivalentes, denotadas\[p\equiv q,\] si\(p \Leftrightarrow q\) es una tautología.

Nota

No escribas\(p = q\); en cambio, escribe\(p \equiv q\).

No estamos diciendo que\(p\) sea igual a\(q\). Dado que\(p\) y\(q\) representan dos declaraciones distintas, no pueden ser iguales. Lo que estamos diciendo es que siempre producen el mismo valor de verdad, independientemente de los valores de verdad de las variables proposicionales subyacentes. Por eso escribimos\(p\equiv q\) en vez de\(p=q\).

Ejemplo\(\PageIndex{4}\label{eg:logiceq-04}\)

Hemos aprendido eso\[p\Leftrightarrow q \equiv (p\Rightarrow q) \wedge (q\Rightarrow p), \nonumber\] que es la razón por la que llamamos\(p\Leftrightarrow q\) una declaración bicondicional.

Ejemplo\(\PageIndex{5}\label{eg:logiceq-05}\)

Utilice tablas de verdad para verificar las siguientes declaraciones equivalentes.

1. \(p \Rightarrow q \equiv \overline{p} \vee q\). [equiv1]
2. \(p \wedge (q \vee r) \equiv (p \wedge q) \vee (p \wedge r)\). [equiv2]

Contestar

A continuación se representan las tablas de verdad para (a) y (b). \[\begin{array}{|*{5}{c|}} \hline p & q & p\Rightarrow q & \overline{p} & \overline{p}\vee q \\ \hline \text{T} & \text{T} & \text{T} & \text{F} & \text{T} \\ \text{T} & \text{F} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{T} & \text{T} & \text{T} & \text{T} \\ \text{F} & \text{F} & \text{T} & \text{T} & \text{T} \\ \hline \end{array} \nonumber\]\[% \arraygap{1.25} \begin{array}{|*{8}{c|}} \hline p & q & r & q\vee r & p\wedge (q\vee r) & p\wedge q & q\wedge r & (p\wedge q)\vee(p\wedge r) \\ \hline \text{T} & \text{T} & \text{T} & \text{T} & \text{T}\phantom{(q\vee{})} & \text{T} & \text{T} & \text{T} \\ \text{T} & \text{T} & \text{F} & \text{T} & \text{T}\phantom{(q\vee{})} & \text{T} & \text{F} & \text{T} \\ \text{T} & \text{F} & \text{T} & \text{T} & \text{T}\phantom{(q\vee{})} & \text{F} & \text{T} & \text{T} \\ \text{T} & \text{F} & \text{F} & \text{F} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{T} & \text{T} & \text{T} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{T} & \text{F} & \text{T} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{F} & \text{T} & \text{T} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \text{F} & \text{F} & \text{F} & \text{T} & \text{F}\phantom{(q\vee{})} & \text{F} & \text{F} & \text{F} \\ \hline \end{array} \nonumber\]Ejemplo ([equiv1]) es un resultado importante. Dice que\(p \Rightarrow q\) es cierto cuando ocurre una de estas dos cosas: (i) cuando\(p\) es falso, (ii) de lo contrario (cuando\(p\) es verdad)\(q\) debe ser cierto.

ejercicio práctico\(\PageIndex{2}\label{he:logiceq-02}\)

Utilice tablas de verdad para establecer estas equivalencias lógicas.

1. \(p \Rightarrow q \equiv \overline{q} \Rightarrow \overline{p}\)
2. \(p \vee p \equiv p\)
3. \(p \wedge q \equiv \overline{\overline{p} \vee \overline{q}}\)
4. \(p \Leftrightarrow q \equiv (p \Rightarrow q) \wedge (q \Rightarrow p)\)

Contestar

Hemos puesto la mesa para (a), y te dejamos el resto a ti.

\[\begin{array}[t]{|c|c|c|c|c|c|} \hline p & q & p\Rightarrow q & \overline{q} & \overline{p} & \overline{q}\Rightarrow\overline{p} \\ \hline \text{T} & \text{T} &&&& \\ \text{T} & \text{F} &&&& \\ \text{F} & \text{T} &&&& \\ \text{F} & \text{F} &&&& \\ \hline \end{array} \nonumber\]

ejercicio práctico\(\PageIndex{3}\label{he:logiceq-03}\)

El conectivo lógico exclusivo o, denotado\(p\veebar q\), significa cualquiera\(p\) o\(q\) pero no ambos. Consecuentemente,\[p\veebar q \equiv (p\vee q) \wedge \overline{(p\wedge q)} \equiv (p\wedge\overline{q}) \vee (\overline{p}\wedge q). \nonumber\] Construir una tabla de verdad para verificar esta afirmación

Propiedades de Equivalencia Lógica. Denotar por\(T\) y\(F\) una tautología y una contradicción, respectivamente. Tenemos las siguientes propiedades para cualquier variable proposicional\(p\),\(q\), y\(r\).

1. Propiedades conmutativas:\(\begin{array}[t]{l} p \vee q \equiv q \vee p, \\ p \wedge q \equiv q \wedge p. \end{array}\)
2. Propiedades asociativas:\(\begin{array}[t]{l} (p \vee q) \vee r \equiv p \vee (q \vee r), \\ (p \wedge q) \wedge r \equiv p \wedge (q \wedge r). \end{array}\)
3. Leyes distributivas:\(\begin{array}[t]{l} p \vee (q \wedge r) \equiv (p \vee q) \wedge (p \vee r), \\ p \wedge (q \vee r) \equiv (p \wedge q) \vee (p \wedge r). \end{array}\)
4. Leyes idempotentes:\(\begin{array}[t]{l} p \vee p \equiv p, \\ p \wedge p \equiv p. \end{array}\)
5. Las leyes de De Morgan:\(\begin{array}[t]{l} \overline{p\vee q} \equiv \overline{p}\wedge\overline{q}, \\ \overline{p\wedge q} \equiv \overline{p}\vee \overline{q}. \end{array}\)
6. Leyes del medio excluido, o leyes inversas:\(\begin{array}[t]{l} p \vee \overline{p} \equiv T, \\ p \wedge \overline{p} \equiv F. \end{array}\)
7. Leyes de identidad:\(\begin{array}[t]{l} p \vee F \equiv p, \\ p \wedge T \equiv p. \end{array}\)
8. Leyes de dominación:\(\begin{array}[t]{l} p \vee T \equiv T, \\ p \wedge F \equiv F. \end{array}\)
9. Equivalencia de una implicación y su contrapositiva:\(p \Rightarrow q \equiv \overline{q} \Rightarrow \overline{p}\).
10. Escribir una implicación como disyunción:\(p \Rightarrow q \equiv \overline{p} \vee q\).

Asegúrate de memorizar las dos últimas equivalencias, porque las usaremos frecuentemente en el resto del curso.

Observación. Estas propiedades no son fáciles de recordar. En lugar de enfocarse en las fórmulas simbólicas, trata de entender sus significados. Expliquémoslas con palabras, y comparémoslas con operaciones similares sobre los números reales,

1. Propiedades conmutativas: En definitiva, dicen que “el orden de operación no importa”. No importa cuál de las dos afirmaciones lógicas viene primero, el resultado de la conjunción y la disyunción siempre produce el mismo valor de verdad. Compare esto con la adición de números reales:\(x+y=y+x\). La resta no es conmutativa, porque no siempre es cierto eso\(x-y=y-x\). Esto explica por qué tenemos que asegurarnos de que una operación sea conmutativa.
2. Propiedades asociativas: En términos generales, estas propiedades también dicen que “el orden de operación no importa”. Sin embargo, existe una diferencia clave entre ellas y las propiedades conmutativas.
   • Las propiedades conmutativas se aplican a las operaciones en dos sentencias lógicas, pero las propiedades asociativas implican tres sentencias lógicas. Dado que\(\wedge\) y\(\vee\) son operaciones binarias, sólo podemos trabajar en un par de declaraciones a la vez. Dadas las tres declaraciones\(p\)\(q\), y\(r\), apareciendo en ese orden, ¿en qué par de declaraciones debemos operar primero? La respuesta es: no importa. Es el orden de agrupación (de ahí el término asociativo) lo que no importa en las propiedades asociativas.
   • La consecuencia importante de la propiedad asociativa es: ya que no importa en qué par de declaraciones debemos realizar primero la operación, podemos eliminar los paréntesis y escribir, por ejemplo,\[p\vee q\vee r \nonumber\] sin preocuparnos por ninguna confusión.
   • No todas las operaciones son asociativas. La resta no es asociativa. Dados los tres números 5, 7 y 4, en ese orden, ¿cómo debemos llevar a cabo dos restas? Qué interpretación debemos usar:\[(5-7)-4, \qquad\mbox{or}\qquad 5-(7-4)?\nonumber\] Dado que conducen a resultados diferentes, hay que tener cuidado en dónde colocar los paréntesis.
3. Leyes distributivas: Cuando mezclamos dos operaciones diferentes en tres declaraciones lógicas, una de ellas tiene que trabajar primero en un par de declaraciones, formando una operación “interna”. A esto le sigue la operación “externa” para completar la declaración compuesta. Las leyes distributivas dicen que podemos distribuir la operación “externa” sobre la interna.
4. Leyes idempotentes: Cuando se aplica una operación a un par de sentencias lógicas idénticas, el resultado es la misma declaración lógica. Compare esto con la ecuación\(x^2=x\), donde\(x\) es un número real. Es cierto sólo cuando\(x=0\) o\(x=1\). Pero las equivalencias lógicas\(p\vee p\equiv p\) y\(p\wedge p\equiv p\) son ciertas para todos\(p\).
5. Leyes de De Morgan: Cuando negamos una disyunción (respectivamente, una conjunción), tenemos que negar las dos afirmaciones lógicas, y cambiar la operación de disyunción a conjunción (respectivamente, de conjunción a disyunción).
6. Leyes del medio excluido, o leyes inversas: Cualquier afirmación es verdadera o falsa, de ahí\(p\vee\overline{p}\) que siempre sea verdadera. De igual manera, una afirmación no puede ser tanto verdadera como falsa al mismo tiempo, de ahí\(p\wedge\overline{p}\) que siempre sea falsa.
7. Leyes de identidad: Compárelas con la ecuación\(x\cdot1=x\): el valor de\(x\) no cambia después de multiplicar por 1. Llamamos al número 1 la identidad multiplicativa. Para operaciones lógicas, la identidad para disyunción es F, y la identidad para conjunción es T.
8. Leyes de dominación: Compárelas con la ecuación\(x\cdot0=0\) para números reales: el resultado es siempre 0, independientemente del valor\(x\). El “cero” para disyunción es T, y el “cero” para la conjunción es F.

Ejemplo\(\PageIndex{6}\label{eg:logiceq-07}\)

¿De qué es la negación\(2\leq x\leq 3\)? Dar una explicación lógica así como una explicación gráfica.

Contestar

La desigualdad\(2\leq x\leq 3\) significa\[(2\leq x) \wedge (x\leq 3).\] Su negación, según las leyes de De Morgan, es\[(2>x) \vee (x>3).\] La desigualdad\(2\leq x\leq 3\) produce un intervalo cerrado. Su negación produce dos intervalos abiertos. Sus representaciones gráficas en la recta numérica real se representan a continuación.

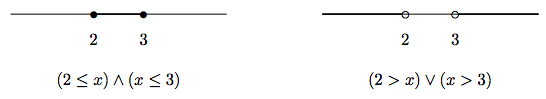
Toma nota de los dos puntos finales 2 y 3. Cambian de inclusión a exclusión cuando tomamos negación.

ejercicio práctico\(\PageIndex{4}\label{he:logiceq-04}\)

Dado que\(0\leq x\leq 1\) significa “\(0\leq x\)y”\(x\leq 1\), su negación debe ser “\(0>x\)o”\(x>1\), que a menudo se escribe como “\(x<0\)o”\(x>1\). Explique por qué es inapropiado, y de hecho incorrecto, escribir “”\(0>x>1\).

ejemplo\(\PageIndex{7}\label{eg:logiceq-08}\)

Ampliar\((p\wedge q)\vee (r\wedge s)\).

Contestar

Compare este problema con la expansión de\((x+y)(u+v)\). Utilizamos la ley distributiva dos veces para obtener\[\begin{aligned} (x+y)(u+v) &=& x(u+v)+y(u+v) \\ &=& xu+xv+yu+yv. \end{aligned} \nonumber\] Sigamos el mismo procedimiento para ampliar\((p\wedge q)\vee(r\wedge s)\). Tenemos que aplicar la ley distributiva dos veces. La primera vez, considerar\((r\wedge s)\) como una sola declaración, y distribuirla sobre ella\(p\wedge q\). En la segunda vuelta, distribuir\(p\) y\(q\), por separado, sobre\(r\wedge s\). La solución completa se muestra a continuación. \[\begin{aligned} (p\wedge q)\vee (r\wedge s) &\equiv& [p\vee (r\wedge s)] \wedge [q\vee(r\wedge s)] \\ &\equiv& (p\vee r)\wedge (p\vee s)\wedge (q\vee r)\wedge (q\vee s). \end{aligned} \nonumber\]También podemos proceder de la siguiente manera:\[\begin{aligned} (p\wedge q)\vee (r\wedge s) &\equiv& [(p\wedge q)\vee r] \wedge [(p\wedge q)\vee s] \\ &\equiv& (p\vee r)\wedge (q\vee r)\wedge (p\vee s)\wedge (q\vee s). \end{aligned} \nonumber\]

Los dos resultados son idénticos porque\(\wedge\) es conmutativo.

ejercicio práctico\(\PageIndex{5}\label{he:logiceq-05}\)

Ampliar\((p\vee q) \wedge (r\vee s)\).

Ejemplo\(\PageIndex{8}\label{eg:logiceq-09}\)

Hemos utilizado una tabla de verdad para verificar que\[[(p \wedge q) \Rightarrow r] \Rightarrow [\overline{r} \Rightarrow (\overline{p} \vee \overline{q})] \nonumber\] es una tautología. Podemos usar las propiedades de equivalencia lógica para mostrar que esta declaración compuesta es lógicamente equivalente a\(T\). Este tipo de pruebas suelen ser más difíciles de seguir, por lo que es una buena idea aportar la explicación en cada paso. Aquí hay una prueba completa:\[% \arraygap{1.2} \begin{array}{lcl@{\quad}l} [(p \wedge q) \Rightarrow r] \Rightarrow [\overline{r} \Rightarrow (\overline{p} \vee \overline{q})] &\equiv& \overline{(p \wedge q) \Rightarrow r} \vee [\overline{r} \Rightarrow (\overline{p} \vee \overline{q})] & \mbox{(implication as disjunction)} \\ &\equiv& \overline{(p \wedge q) \Rightarrow r} \vee [\overline{\overline{p} \vee \overline{q}} \Rightarrow r] & \mbox{(implication as disjunction)} \\ &\equiv& \overline{(p \wedge q) \Rightarrow r} \vee [(p \wedge q) \Rightarrow r] & \mbox{(De Morgan's law)} \\ &\equiv& T & \mbox{(inverse law)} \end{array} \nonumber\] Esto es precisamente lo que llamamos el método de izquierda a derecha para probar una identidad (en este caso, una equivalencia lógica).

Ejemplo\(\PageIndex{9}\label{eg:logiceq-10}\)

Escribir\(\overline{p \Rightarrow q}\) como conjunción.

Contestar

Es importante recordar eso\[\overline{p\Rightarrow q} \not\equiv q\Rightarrow p, \nonumber\] y\[\overline{p\Rightarrow q} \not\equiv \overline{p}\Rightarrow\overline{q} \nonumber\] cualquiera de los dos. En cambio, ya que\(p\Rightarrow q \equiv \overline{p}\vee q\), se deduce de la ley de De Morgan que\[\overline{p \Rightarrow q} \equiv \overline{\overline{p} \vee q} \equiv p \wedge \overline{q}. \nonumber\] Alternativamente, podemos argumentar de la siguiente manera. Interpretar\(\overline{p \Rightarrow q}\) como decir\(p \Rightarrow q\) es falso. Esto requiere\(p\) ser verdadero y\(q\) ser falso, lo que se traduce en\(p \wedge \overline{q}\). Por lo tanto,\(\overline{p\Rightarrow q} \equiv p\wedge \overline{q}\).

Resumen y revisión

• Dos afirmaciones lógicas son lógicamente equivalentes si siempre producen el mismo valor de verdad.
• En consecuencia,\(p\equiv q\) es lo mismo que decir\(p\Leftrightarrow q\) es una tautología.
• Además de las leyes distributivas y de De Morgan, recuerde también estas dos equivalencias; son muy útiles a la hora de tratar las implicaciones. \[p \Rightarrow q \equiv \overline{q} \Rightarrow \overline{p} \qquad\mbox{and}\qquad p \Rightarrow q \equiv \overline{p} \vee q. \nonumber\]

Ejercicios 2.5

Ejercicio\(\PageIndex{1}\label{ex:logiceq-01}\)

Usa una tabla de verdad para verificar la ley de De Morgan\(\overline{p\vee q} \equiv \overline{p}\wedge\overline{q}\).

Ejercicio\(\PageIndex{2}\label{ex:logiceq-02}\)

Utilice tablas de verdad para verificar las dos propiedades asociativas.

Ejercicio\(\PageIndex{3}\label{ex:logiceq-03}\)

Construya una tabla de verdad para cada fórmula a continuación. ¿Cuáles son las tautologías?

1. \((\overline{p} \vee q)\Rightarrow p\)
2. \((p\Rightarrow q) \vee (p\Rightarrow \overline{q})\)
3. \((p\Rightarrow q) \Rightarrow r\)

Ejercicio\(\PageIndex{4}\label{ex:logiceq-04}\)

Utilice tablas de verdad para verificar estas equivalencias lógicas.

1. \((p\wedge q)\Leftrightarrow p \equiv p\Rightarrow q\)
2. \((p\wedge q)\Rightarrow r \equiv p\Rightarrow(\overline{q}\vee r)\)
3. \((p\Rightarrow\overline{q}) \wedge (p\Rightarrow\overline{r}) \equiv \overline{p\wedge(q\vee r)}\)

Contestar

Agrega textos aquí. No elimine primero este texto.

Ejercicio\(\PageIndex{5}\label{ex:logiceq-05}\)

Utilice únicamente las propiedades de equivalencias lógicas para verificar (b) y (c) en el Problema 4.

Ejercicio\(\PageIndex{6}\label{ex:logiceq-06}\)

Determine si las fórmulas\(u\) y\(v\) son lógicamente equivalentes (puede usar tablas de verdad o propiedades de equivalencias lógicas).

\(u:\;(p\Rightarrow q)\wedge (p\Rightarrow\overline{q})\)

\(v:\;\overline{p}\)

\(u:\;p\Rightarrow q\)

\(v:\;q\Rightarrow p\)

\(u:\;p\Leftrightarrow q\)

\(v:\;q\Leftrightarrow p\)

\(u:\;(p\Rightarrow q)\Rightarrow r\)

\(v:\;p\Rightarrow(q\Rightarrow r)\)

Ejercicio\(\PageIndex{7}\label{ex:logiceq-07}\)

Encuentra lo contrario, inverso y contrapositivo de estas implicaciones.

1. Si el triángulo\(ABC\) es isósceles y contiene un ángulo de 45 grados, entonces\(ABC\) es un triángulo rectángulo.
2. Si el cuadrilátero\(ABCD\) es un cuadrado, entonces es tanto un rectángulo como un rombo.
3. Si el cuadrilátero\(ABCD\) tiene dos lados de igual longitud, entonces es un rectángulo o un rombo.

Ejercicio\(\PageIndex{8}\label{ex:logiceq-08}\)

Negar las siguientes implicaciones:

1. \(x^2>0 \Rightarrow x>0\).
2. Si\(PQRS\) es un cuadrado, entonces\(PQRS\) es un paralelogramo.
3. Si\(n>1\) es primo, entonces\(n+1\) es compuesto.
4. Si\(x\) y\(y\) son enteros tales que\(xy\geq1\), entonces cualquiera\(x\geq1\) o\(y\geq1\).

Ejercicio\(\PageIndex{9}\label{ex:logiceq-09}\)

Determine si las siguientes fórmulas son verdaderas o falsas:

1. \(\overline{p\Leftrightarrow q} \equiv \overline{p} \Leftrightarrow \overline{q}\)
2. \((p\Rightarrow q) \vee (p\Rightarrow\overline{q}) \equiv \overline{p}\)
3. \(p\Rightarrow q \equiv q\Rightarrow p\)

Ejercicio\(\PageIndex{10}\label{ex:logiceq-10}\)

Determine si las siguientes fórmulas son verdaderas o falsas:

1. \((p\Rightarrow q)\Rightarrow r \equiv p\Rightarrow (q\Rightarrow r)\)
2. \(p\Rightarrow (q\vee r) \equiv (p\Rightarrow q) \vee (p\Rightarrow r)\)
3. \(p\Rightarrow (q\wedge r) \equiv (p\Rightarrow q) \wedge (p\Rightarrow r)\)

Ejercicio\(\PageIndex{11}\label{ex:logiceq-11}\)

¿Cuáles de las siguientes afirmaciones equivalen a la declaración “si\(x^2>0\), entonces\(x>0\)”?

1. Si\(x>0\), entonces\(x^2>0\).
2. Si\(x\leq0\), entonces\(x^2\leq0\).
3. Si\(x^2\leq0\), entonces\(x\leq0\).
4. Si\(x^2\not>0\), entonces\(x\not>0\).

Ejercicio\(\PageIndex{12}\label{ex:logiceq-12}\)

Determine si las siguientes fórmulas son tautologías, contradicciones o ninguna:

1. \((p\Rightarrow q) \wedge \overline{p}\)
2. \((p\Rightarrow\overline{q}) \wedge (p\wedge q)\)
3. \((p\Rightarrow\overline{q}) \wedge q\)

Ejercicio\(\PageIndex{13}\label{ex:logiceq-13}\)

Simplifique las siguientes fórmulas:

1. \(p\wedge(p\wedge q)\)
2. \(\overline{\overline{p}\vee q}\)
3. \(\overline{p\Rightarrow\overline{q}}\)

Ejercicio\(\PageIndex{14}\label{ex:logiceq-14}\)

Simplifique las siguientes fórmulas:

1. \((p\Rightarrow\overline{q}) \wedge (\overline{q}\Rightarrow p)\)
2. \(\overline{p\wedge\overline{q}}\)
3. \(p\wedge(\overline{p}\vee q)\)