4.3: Sindicatos e Intersecciones

Podemos formar un nuevo conjunto a partir de conjuntos existentes mediante la realización de una operación de conjunto.

Definición: intersección

Dados dos conjuntos\(A\) y\(B\), definir su intersección para que sea el conjunto

\[A \cap B = \{ x\in{\cal U} \mid x \in A \wedge x \in B \} \nonumber\]

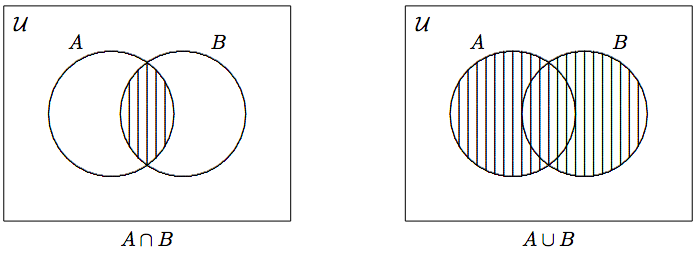
Hablando vagamente,\(A \cap B\) contiene elementos comunes a ambos\(A\) y\(B\).

Definición

La unión de\(A\) y\(B\) se define como

\[A \cup B = \{ x\in{\cal U} \mid x \in A \vee x \in B \} \nonumber\]

Así\(A \cup B\) es, como su nombre indica, el conjunto que combina todos los elementos de\(A\) y\(B\).

Definición

La diferencia establecida\(A-B\), a veces escrita como\(A \setminus B\), se define como

\[A- B = \{ x\in{\cal U} \mid x \in A \wedge x \not\in B \} \nonumber\]

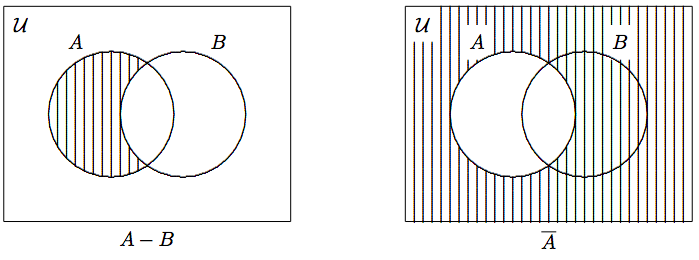
En palabras,\(A-B\) contiene elementos que sólo se pueden encontrar en\(A\) pero no en\(B\). Operacionalmente hablando,\(A-B\) es el conjunto obtenido de\(A\) quitando los elementos a los que también pertenecen\(B\). Por lo tanto, la diferencia establecida también\(A-B\) se llama el complemento relativo de\(B\) in\(A\). En particular,\({\cal U}-A\) se llama el complemento de\(A\), y se denota por\(\overline{A}\),\(A'\) o\(A^c\).

Comentario

Nos gustaría recordar a los lectores que no es raro entre los autores adoptar diferentes notaciones para un mismo concepto matemático. De igual manera, la misma notación podría significar algo diferente en otro libro de texto o incluso otra rama de las matemáticas. Es importante desarrollar el hábito de examinar el contexto y asegurarse de que entiendes el significado de las notaciones cuando empiezas a leer una exposición matemática.

Ejemplo\(\PageIndex{1}\label{eg:unionint-01}\)

Vamos\({\cal U}=\{1,2,3,4,5\}\),\(A=\{1,2,3\}\), y\(B=\{3,4\}\). Encontrar\(A\cap B\),\(A\cup B\),\(A-B\),\(B-A\),\(\overline{A}\), y\(\overline{B}\).

Solución

Tenemos También\[\begin{array}{r c l} A\cap B &=& \{3\}, \\ A\cup B &=& \{1,2,3,4\}, \\ A - B &=& \{1,2\}, \\ B - A &=& \{4\}. \end{array} \nonumber\] encontramos\(\overline{A} = \{4,5\}\), y\(\overline{B} = \{1,2,5\}\).

ejercicio práctico\(\PageIndex{1}\label{he:unionint-01}\)

Vamos\({\cal U} = \{\mbox{John}, \mbox{Mary}, \mbox{Dave}, \mbox{Lucy}, \mbox{Peter}, \mbox{Larry}\}\),\[A = \{\mbox{John}, \mbox{Mary}, \mbox{Dave}\}, \qquad\mbox{and}\qquad B = \{\mbox{John}, \mbox{Larry}, \mbox{Lucy}\}. \nonumber\] Encuentra\(A\cap B\),\(A\cup B\),\(A-B\),\(B-A\),\(\overline{A}\), y\(\overline{B}\).

ejercicio práctico\(\PageIndex{2}\label{he:unionint-02}\)

Si\(A\subseteq B\), ¿cuál sería\(A-B\)?

Ejemplo\(\PageIndex{2}\label{eg:unionint-02}\)

El conjunto de enteros se puede escribir como el\[\mathbb{Z} = \{-1,-2,-3,\ldots\} \cup \{0\} \cup \{1,2,3,\ldots\}. \nonumber\] ¿Podemos reemplazar\(\{0\}\) con 0? Explique.

ejercicio práctico\(\PageIndex{3}\label{he:unionint-03}\)

Explica por qué las siguientes expresiones son sintácticamente incorrectas.

1. \(\mathbb{Z} = \{-1,-2,-3,\ldots\} \cup \;0\; \cup \{1,2,3,\ldots\}\).
2. \(\mathbb{Z} = \ldots,-3,-2,-1 \;\cup\; 0 \;\cup\; 1,2,3,\ldots\,\)
3. \(\mathbb{Z} = \ldots,-3,-2,-1 \;+\; 0 \;+\; 1,2,3,\ldots\,\)
4. \(\mathbb{Z} = \mathbb{Z} ^- \;\cup\; 0 \;\cup\; \mathbb{Z} ^+\)

¿Cómo arreglarías los errores en estas expresiones?

Ejemplo\(\PageIndex{3}\label{eg:unionint-03}\)

Para cualquier conjunto\(A\), ¿qué son\(A\cap\emptyset\)\(A\cup\emptyset\),\(A-\emptyset\),\(\emptyset-A\) y\(\overline{\overline{A}}\)?

Contestar

Es claro que\[A\cap\emptyset = \emptyset, \qquad A\cup\emptyset = A, \qquad\mbox{and}\qquad A-\emptyset = A. \nonumber\] A partir de la definición de diferencia de conjunto, nos encontramos\(\emptyset-A = \emptyset\). Por último,\(\overline{\overline{A}} = A\).

Ejemplo\(\PageIndex{4}\label{eg:unionint-04}\)

Escribir, en notación de intervalos,\([5,8)\cup(6,9]\) y\([5,8)\cap(6,9]\).

Contestar

Las respuestas son\[[5,8)\cup(6,9] = [5,9], \qquad\mbox{and}\qquad [5,8)\cap(6,9] = (6,8). \nonumber\] Se obtienen comparando la ubicación de los dos intervalos en la recta numérica real.

ejercicio práctico\(\PageIndex{4}\label{he:unionint-04}\)

Escribir, en notación de intervalos,\((0,3)\cup[-1,2)\) y\((0,3)\cap[-1,2)\).

Ejemplo\(\PageIndex{5}\label{eg:unionint-05}\)

Ahora podemos describir el siguiente conjunto\[\{x\in\mathbb{R} \mid (x<5) \vee (x>7)\} \nonumber\] en la notación de intervalo. Se puede escribir como cualquiera\((-\infty,5)\cup(7,\infty)\) o, usando complemento,\(\mathbb{R}-[5,7\,]\). En consecuencia, decir\(x\notin[5,7\,]\) es lo mismo que decir\(x\in(-\infty,5) \cup(7,\infty)\), o equivalentemente,\(x\in \mathbb{R}-[5,7\,]\).

Teorema\(\PageIndex{1}\label{thm:setprop}\)

Las siguientes propiedades son válidas para cualquier conjunto\(A\)\(B\), y\(C\) en un conjunto universal\({\cal U}\).

1. Propiedades conmutativas:\(\begin{array}[t]{l} A \cup B = B \cup A, \\ A \cap B = B \cap A. \end{array}\)
2. Propiedades asociativas:\(\begin{array}[t]{l} (A \cup B) \cup C = A \cup (B \cup C), \\ (A \cap B) \cap C = A \cap (B \cap C). \end{array}\)
3. Leyes distributivas:\(\begin{array}[t]{l} A \cup (B \cap C) = (A \cup B) \cap (A \cup C), \\ A \cap (B \cup C) = (A \cap B) \cup (A \cap C). \end{array}\)
4. Leyes idempotentes:\(\begin{array}[t]{l} A \cup A = A, \\ A \cap A = A. \end{array}\)
5. Las leyes de De Morgan:\(\begin{array}[t]{l} \overline{A \cup B} = \overline{A} \cap \overline{B}, \\ \overline{A \cap B} = \overline{A} \cup \overline{B}. \end{array}\)
6. Leyes del medio excluido, o leyes inversas:\(\begin{array}[t]{l} A \cup \overline{A} = {\cal U}, \\ A \cap \overline{A} = \emptyset. \end{array}\)

A modo de ilustración, probaremos la ley distributiva\[A \cup (B \cap C) = (A \cup B) \cap (A \cup C). \nonumber\] Necesitamos demostrar que\[\forall x\in{\cal U}\, \big[x \in A \cup (B \cap C) \Leftrightarrow x \in (A \cup B) \cap (A \cup C) \big]. \nonumber\] Equivalentemente, necesitamos demostrar que De\[A \cup (B \cap C) \subseteq (A \cup B) \cap (A \cup C), \qquad\mbox{and}\qquad (A \cup B) \cap (A \cup C) \subseteq A \cup (B \cap C). \nonumber\] cualquier manera, necesitamos establecer la igualdad en dos pasos.

Presentamos ahora dos pruebas del derecho distributivo\(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\).

Prueba 1

Vamos\(x\in A\cup(B\cap C)\). Entonces\(x\in A\), o\(x\in B\cap C\). Sabemos que eso\(x\in B\cap C\) implica eso\(x\in B\) y\(x\in C\). Así que tenemos

1. \(x\in A\)o\(x\in B\), y
2. \(x\in A\)o\(x\in C\);

equivalentemente,

1. \(x\in A\cup B\), y
2. \(x\in A\cup C\).

Así,\(x\in (A\cup B)\cap (A\cup C)\). Eso lo hemos demostrado\(A\cup(B\cap C) \subseteq (A\cup B)\cap(A\cup C)\).

Ahora vamos\(x\in (A\cup B)\cap(A\cup C)\). Entonces\(x\in A\cup B\) y\(x\in A\cup C\). A partir de la definición de unión, encontramos

1. \(x\in A\)o\(x\in B\), y
2. \(x\in A\)o\(x\in C\).

Ambas condiciones lo requieren\(x\in A\), así podemos reescribirlas como

1. \(x\in A\), o
2. \(x\in B\)y\(x\in C\);

equivalentemente,

1. \(x\in A\), o
2. \(x\in B\cap C\).

Así,\(x\in A\cup(B\cap C)\). Esto lo demuestra\((A\cup B)\cap(A\cup C) \subseteq A\cup(B\cap C)\). Junto con\(A\cup(B\cap C) \subseteq (A\cup B)\cap(A\cup C)\), concluimos que\(A\cup(B\cap C) = (A\cup B) \cap(A\cup C)\).

A continuación se muestra una prueba alternativa. Este tipo de argumento es más corto, pero es más simbólico; de ahí que sea más difícil de seguir.

Prueba 2

Ya que de\[ \begin{array}{r l l} x \in A \cup (B \cap C) & \Leftrightarrow x \in A \vee x \in (B \cap C) & (\text{defn. of union}) \\ & \Leftrightarrow x \in A \vee (x \in B \wedge x \in C) & (\text{defn. of intersection}) \\ & \Leftrightarrow (x \in A \vee x \in B) \wedge (x \in A \vee x \in C) & (\text{distributive law}) \\ & \Leftrightarrow (x \in A \cup B) \wedge (x \in A \cup C) & (\text{defn. of union}) \\ & \Leftrightarrow x \in (A \cup B) \cap (A \cup B) & (\text{defn. of intersection}) \end{array} \nonumber\] ello se deduce que\(A \cup (B \cap C) = (A\cup B) \cap (A\cup C)\).

ejercicio práctico\(\PageIndex{5}\label{he:unionint-05}\)

\(A\cap(B\cup C) = (A\cap B)\cup(A\cap C)\)Demuéstralo.

ejercicio práctico\(\PageIndex{6}\label{he:unionint-06}\)

Demostrar que si\(A\subseteq B\) y\(A\subseteq C\), entonces\(A\subseteq B\cap C\).

Discusión

Empecemos con un borrador. El enunciado que queremos probar toma la forma de\[(A\subseteq B) \wedge (A\subseteq C) \Rightarrow A\subseteq B\cap C. \nonumber\] De ahí, ¿qué asumimos y qué queremos probar?

Asumir:

Quiere Demostrar:

¿Asumiste nosotros asumimos\(A\subseteq B\) y\(A\subseteq C\), y queremos probarlo\(A\subseteq B\cap C\)? ¡Genial! Ahora bien, ¿qué quiere decir con\(A\subseteq B\)? ¿Qué tal\(A\subseteq C\)? ¿Cuál es el significado de\(A\subseteq B\cap C\)?

\(A\subseteq B\)significa: Para cualquiera\(x\in{\cal U}\), si\(x\in A\), entonces\(x\in B\) también.

\(A\subseteq C\)significa:

\(A\subseteq B\cap C\)significa:

¿Cómo se pueden utilizar los dos primeros datos para obtener lo que necesitamos establecer?

Ahora es el momento de armar todo, y pulirlo en una versión final. Recuerda tres cosas:

1. el esquema de la prueba,
2. la razón en cada paso del argumento principal, y
3. la introducción y la conclusión.

Ponga la prueba completa en el espacio de abajo.

Aquí hay dos resultados que involucran complementos.

Teorema\(\PageIndex{1}\label{thm:subsetsbar}\)

Para dos conjuntos cualquiera\(A\) y\(B\), tenemos\(A \subseteq B \Leftrightarrow \overline{B} \subseteq \overline{A}\).

Teorema\(\PageIndex{1}\label{thm:genDeMor}\)

Para cualquier juego\(A\)\(C\),\(B\) y\[\begin{aligned} A-(B\cup C) &=& (A-B)\cap(A-C), \\ A-(B\cap C) &=& (A-B)\cup(A-C), \end{aligned} \nonumber\]

Resumen y revisión

• Memorice las definiciones de intersección, unión y diferencia de conjunto. Confiamos en ellos para probar o derivar nuevos resultados.
• La intersección de dos conjuntos\(A\) y\(B\), denotado\(A\cap B\), es el conjunto de elementos comunes a ambos\(A\) y\(B\). En símbolos,\(\forall x\in{\cal U}\,\big[x\in A\cap B \Leftrightarrow (x\in A \wedge x\in B)\big]\).
• La unión de dos conjuntos\(A\) y\(B\), denotado\(A\cup B\), es el conjunto que combina todos los elementos en\(A\) y\(B\). En símbolos,\(\forall x\in{\cal U}\,\big[x\in A\cap B \Leftrightarrow (x\in A\vee x\in B)\big]\).
• La diferencia de conjunto entre dos conjuntos\(A\) y\(B\), denotada por\(A-B\), es el conjunto de elementos que solo se pueden encontrar en\(A\) pero no en\(B\). En símbolo, significa\(\forall x\in{\cal U}\, \big[x\in A-B \Leftrightarrow (x\in A \wedge x\notin B)\big]\).
• Conocer las propiedades de intersección, unión y diferencias de conjunto enumeradas en el Teorema 4.3.1.

Ejercicio\(\PageIndex{1}\label{ex:unionint-01}\)

Escribe cada uno de los siguientes conjuntos enumerando sus elementos explícitamente.

1. \([-4,4]\cap\mathbb{Z}\)
2. \((-4,4]\cap\mathbb{Z}\)
3. \((-4,\infty)\cap\mathbb{Z}\)
4. \((-\infty,4]\cap\mathbb{N}\)
5. \((-4,\infty)\cap\mathbb{Z}^-\)
6. \((4,5)\cap\mathbb{Z}\)

Ejercicio\(\PageIndex{2}\label{ex:unionint-02}\)

Asumir\({\cal U} = \mathbb{Z}\), y dejar

\[ \begin{array}{c} A=\{\ldots, -6,-4,-2,0,2,4,6, \ldots \} = 2\mathbb{Z}, \\ B=\{\ldots, -9,-6,-3,0,3,6,9, \ldots \} = 3\mathbb{Z}, \\ C=\{\ldots, -12,-8,-4,0,4,8,12, \ldots \} = 4\mathbb{Z}. \end{array} \nonumber\]

Describa los siguientes conjuntos enumerando sus elementos explícitamente.

1. \(A\cap B\)
2. \(C-A\)
3. \(A-B\)
4. \(A\cap\overline{B}\)
5. \(B-A\)
6. \(B\cup C\)
7. \((A\cup B)\cap C\)
8. \((A\cup B)-C\)

Ejercicio\(\PageIndex{3}\label{ex:unionint-03}\)

¿Estas afirmaciones son verdaderas o falsas?

• \([1,2]\cap[2,3] = \emptyset\)
• \([1,2)\cup(2,3] = [2,3]\)

Ejercicio\(\PageIndex{4}\label{ex:unionint-04}\)

Que el conjunto universal\({\cal U}\) sea el conjunto de personas que votaron en las elecciones presidenciales de Estados Unidos de 2012. Defina los subconjuntos\(D\),\(B\), y\(W\) de la\({\cal U}\) siguiente manera:\[\begin{array}{r c l} D &=& \{x\in{\cal U} \mid x \mbox{ registered as a Democrat}\}, \\ B &=& \{x\in{\cal U} \mid x \mbox{ voted for Barack Obama}\}, \\ W &=& \{x\in{\cal U} \mid x \mbox{ belonged to a union}\}. \end{array} \nonumber\] Expresar los siguientes subconjuntos de\({\cal U}\) en términos de\(D\),\(B\), y\(W\).

1. Gente que no votó por Barack Obama.
2. Miembros del sindicato que votaron por Barack Obama.
3. Demócratas registrados que votaron por Barack Obama pero que no pertenecían a un sindicato.
4. Miembros del sindicato que o no estaban registrados como demócratas o votaron por Barack Obama.
5. Personas que votaron por Barack Obama pero no estaban registradas como demócratas y no eran sindicalistas.
6. Personas que estaban registradas como demócratas y eran miembros del sindicato, o no votaron por Barack Obama.

Ejercicio\(\PageIndex{5}\label{ex:unionint-05}\)

Una compañía de seguros clasifica su conjunto\({\cal U}\) de tomadores de pólizas por los siguientes conjuntos:\[\begin{array}{r c l} A &=& \{x\mid x\mbox{ drives a subcompact car}\}, \\ B &=& \{x\mid x\mbox{ drives a car older than 5 years}\}, \\ C &=& \{x\mid x\mbox{ is married}\}, \\ D &=& \{x\mid x\mbox{ is over 21 years old}\}, \\ E &=& \{x\mid x\mbox{ is a male}\}. \end{array} \nonumber\] Describa cada uno de los siguientes subconjuntos de\({\cal U}\) en términos de\(A\)\(B\),\(C\),\(D\), y\(E\).

1. Pólizas masculinas mayores de 21 años.
2. Los tomadores de pólizas que sean mujeres o conduzcan autos de más de 5 años.
3. Mujeres aseguradoras mayores de 21 años que manejan autos subcompactos.
4. Los tomadores de pólizas de sexo masculino que estén casados o mayores de 21 años y no manejen autos subcompactos.

Ejercicio\(\PageIndex{6}\label{ex:unionint-06}\)

Dejar\(A\) y\(B\) ser conjuntos arbitrarios. Complete las siguientes declaraciones.

1. \(A\subseteq B \Leftrightarrow A\cap B = ~ \rule{3cm}{0.4pt}\).
2. \(A\subseteq B \Leftrightarrow A\cup B = ~ \rule{3cm}{0.4pt}\).
3. \(A\subseteq B \Leftrightarrow A - B = ~ \rule{3cm}{0.4pt}\).
4. \(A\subset B \Leftrightarrow (A-B=~ \rule{3cm}{0.4pt}\,\wedge\,B-A\neq~ \rule{3cm}{0.4pt}\,)\).
5. \(A\subset B \Leftrightarrow (A\cap B=~ \rule{3cm}{0.4pt}\,\wedge\,A\cap B\neq~ \rule{3cm}{0.4pt}\,)\).
6. \(A - B = B - A \Leftrightarrow ~ \rule{3cm}{0.4pt}\,\).

Ejercicio\(\PageIndex{7}\label{ex:unionint-07}\)

Dar ejemplos de conjuntos\(A\) y\(B\) tal que\(A\in B\) y\(A\subset B\).

Ejercicio\(\PageIndex{8}\label{ex:unionint-08}\)

Demostrar las leyes de De Morgan.

Ejercicio\(\PageIndex{9}\label{ex:unionint-09}\)

Dejar\(A\),\(B\), y\(C\) ser cualquiera de tres conjuntos. Demostrar que si\(A\subseteq C\) y\(B\subseteq C\), entonces\(A\cup B\subseteq C\).

Ejercicio\(\PageIndex{10}\label{ex:unionint-10}\)

Teorema de Probar 4.3.2

Ejercicio\(\PageIndex{11}\label{ex:unionint-11}\)

Teorema de Probar 4.3.3

Ejercicio\(\PageIndex{12}\label{ex:unionint-12}\)

Dejar\(A\),\(B\), y\(C\) ser cualquiera de tres conjuntos. Demostrar que

1. \(A-B=A\cap\overline{B}\)
2. \(A=(A-B)\cup(A\cap B)\)
3. \(A-(B-C) = A\cap(\overline{B}\cup C)\)
4. \((A-B)-C = A-(B\cup C)\)

Ejercicio\(\PageIndex{13}\label{ex:unionint-13}\)

Comentar las siguientes declaraciones. ¿Son sintácticamente correctos?

1. \(x\in A \cap x\in B \equiv x\in A\cap B\)
2. \(x\in A\wedge B \Rightarrow x\in A\cap B\)

Ejercicio\(\PageIndex{14}\label{ex:unionint-14}\)

Demostrar o desacreditar cada una de las siguientes afirmaciones sobre conjuntos arbitrarios\(A\) y\(B\). Si crees que una afirmación es verdadera, demuéstrala; si crees que es falsa, da un contraejemplo.

1. \(\wp(A\cap B) = \wp(A)\cap\wp(B)\)
2. \(\wp(A\cup B) = \wp(A)\cup\wp(B)\)
3. \(\wp(A - B) = \wp(A) - \wp(B)\)

Observación

Para demostrar que dos sets\(U\) y\(V\) son iguales, por lo general queremos demostrarlo\(x\in U \Leftrightarrow x\in V\). En este problema, el elemento\(x\) es en realidad un conjunto. Como solemos usar letras mayúsculas para denotar conjuntos, debemos comenzar la prueba de (a) con “Let”\(S\in\wp(A\cap B)\). Si prefiere utilizar el enfoque alternativo, parece lo siguiente:\[\begin{array}{r c l} S\in\wp(A\cap B) &\Leftrightarrow& \ldots \\ &\Leftrightarrow& \ldots \\ &\vdots& \\ &\Leftrightarrow& S\in\wp(A)\cap\wp(B). \end{array} \nonumber\] Estas observaciones también se aplican a los apartados b) y c).