4.5: Conjuntos de índices

La noción de unión puede extenderse a tres conjuntos:\[A\cup B\cup C = \{x\in{\cal U} \mid (x\in A) \vee (x\in B) \vee (x\in C) \}. \nonumber\] Es obvio cómo generalizarla a la unión de cualquier número de conjuntos. Usamos una notación que se asemeja a la notación de suma para describir tal unión:\[\bigcup_{i=1}^n A_i = A_1 \cup A_2 \cup \cdots \cup A_n. \nonumber\] Definimos

\[\bigcup_{i=1}^n A_i = \{x\in{\cal U} \mid (x\in A_1) \vee (x\in A_2) \vee\cdots\vee (x\in A_n)\}. \nonumber\]¡Se ve desordenado! Aquí hay una mejor alternativa:

\[\bigcup_{i=1}^n A_i =\{x\in{\cal U} \mid x\in A_i \mbox{ for } some \, \, i, \mbox{ where } 1\leq i \leq n\}. \nonumber\]

De manera similar,\(\bigcap_{i=1}^n A_i = A_1 \cap A_2 \cap \cdots \cap A_n\), y definimos

\ [\ bigcap_ {i=1} ^n a_I
=\ {x\ in {\ cal U}\ mid x\ in a_i\ mbox {para} todos\,\, i,
\ mbox {donde} 1\ leq i\ leq n\}\ nonumber\]

En inglés sencillo,\(\bigcup_{i=1}^n A_i\) es la colección de todos los elementos en los\(A_i\)'s, y\(\bigcap_{i=1}^n A_n\) es la colección de todos los elementos comunes a todos los\(A_i\)'s.

Ejemplo\(\PageIndex{1}\label{eg:indexset-01}\)

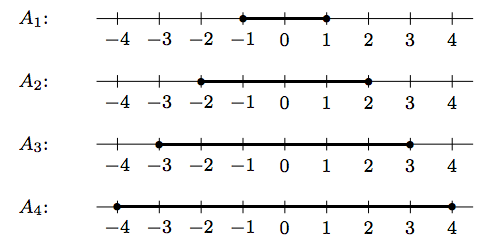
Para\(i=1,2,3,\ldots\,\), vamos\(A_i = [-i,i]\). En primer lugar, construir varios\(A_i\) para la comparación, ya que puede ayudarnos a detectar cualquier patrón específico. Vea la Figura\(\PageIndex{1}\) a continuación. Eso es claro\(A_1 \subset A_2 \subset \cdots\,\). Así,\(\bigcup_{i=1}^n A_i = [-n,n] = A_n\), y\(\bigcap_{i=1}^n A_i = [-1,1] = A_1\).

Figura\(\PageIndex{1}\): Comparando intervalos para encontrar su unión e intersección.

Ejercicio práctico\(\PageIndex{1}\label{he:indexset-01}\)

Evaluar\(\bigcup_{i=1}^n B_i\) y\(\bigcap_{i=1}^n B_i\), dónde\(B_i = [0,2i)\).

Es obvio que también podemos extender el límite superior hasta el infinito. \[\begin{aligned} \bigcup_{i=1}^\infty A_i &=& A_1 \cup A_2 \cup \cdots = \{ x\in{\cal U} \mid x\in A_i \mbox{ for }some \, \, i \in \mathbb{N} \}, \\ \bigcap_{i=1}^\infty A_i &=& A_1 \cap A_2 \cap \cdots = \{ x\in{\cal U} \mid x\in A_i \mbox{ for } all \, \, i \in \mathbb{N} \}. \end{aligned} \nonumber\]En algunas situaciones, podemos tomar prestada la idea de sumas parciales del cálculo. Primero encontramos la unión o intersección de los primeros\(n\) conjuntos, luego tomamos el límite a medida que se\(n\) acerca al infinito. Por lo tanto, si el límite está bien definido,

\[\bigcup_{i=1}^\infty A_i = \lim_{n\to\infty} \bigcup_{i=1}^n A_i, \qquad\mbox{and}\qquad \bigcap_{i=1}^\infty A_i = \lim_{n\to\infty} \bigcap_{i=1}^n A_i. \nonumber\]

Ejemplo\(\PageIndex{2}\label{eg:indexset-02}\)

Vamos\(A_i = [-i,i]\). Hemos aprendido del último ejemplo que\(\bigcup_{i=1}^n A_i = [-n,n]\) y\(\bigcap_{i=1}^n A_i = [-1,1]\). De ahí,\[\bigcup_{i=1}^\infty A_i = \lim_{n\to\infty} [-n,n] = (-\infty,\infty), \qquad\mbox{and}\qquad \bigcap_{i=1}^\infty A_i = [-1,1]. \nonumber\] Recordemos que escribimos\((-\infty,\infty)\) en vez de\([-\infty,\infty]\) porque no\(\pm\infty\) son números, son meramente símbolos que representan valores infinitamente grandes.

Ejercicio práctico\(\PageIndex{2}\label{he:indexset-02}\)

Evaluar\(\bigcup_{i=1}^\infty B_i\) y\(\bigcap_{i=1}^\infty B_i\), dónde\(B_i = [0,2i)\).

Ejemplo\(\PageIndex{3}\label{eg:indexset-03}\)

Vamos\(B_i = \left(0,1-\frac{1}{2i}\right]\). Determinar\(\bigcup_{i=1}^\infty B_i\) y\(\bigcap_{i=1}^\infty B_i\).

Solución

Una vez más, tenemos\(B_1 \subset B_2 \subset \cdots\,\). Es fácil comprobar que De\[\bigcup_{i=1}^n B_i = B_n = \left(0,1-\frac{1}{2n}\right], \qquad\mbox{and}\qquad \bigcap_{i=1}^n B_i = B_1 = \left(0,\frac{1}{2}\right]. \nonumber\] ello se deduce que\[\bigcup_{i=1}^\infty B_i = \lim_{n\to\infty} \left(0,1-\frac{1}{2n}\right] = (0,1), \qquad\mbox{and}\qquad \bigcap_{i=1}^\infty B_i = \left(0,\frac{1}{2}\right]. \nonumber\] Tenga en cuenta que\(\lim_{n\to\infty} \left(0,1-\frac{1}{2n}\right] \neq (0,1]\) debido a que el punto final 1 no pertenece a ninguna\(B_i\).

Ejercicio práctico\(\PageIndex{3}\label{he:indexset-03}\)

Vamos\(C_i = \left[0,1-\frac{1}{i}\right]\). Determinar\(\bigcup_{i=1}^\infty C_i\) y\(\bigcap_{i=1}^\infty C_i\).

Ejemplo\(\PageIndex{4}\label{eg:indexset-04}\)

Vamos\(D_i = \left(1-\frac{1}{i},1+\frac{1}{i}\right)\). Determinar\(\bigcup_{i=1}^\infty D_i\) y\(\bigcap_{i=1}^\infty D_i\).

Solución

A medida que\(i\) aumenta el valor de,\(\frac{1}{i}\) disminuye el valor de. Por lo tanto, el punto final izquierdo\(1-\frac{1}{i}\) aumenta y el punto final derecho\(1+\frac{1}{i}\) disminuye.

\[\begin{array}{|c|c|} \hline i & D_i = \big(1-\frac{1}{i},1+\frac{1}{i}\big) \\ \hline 1 & (0,2) \\ 2 & \big(\frac{1}{2},\frac{3}{2}\big) \\ 3 & \big(\frac{2}{3},\frac{4}{3}\big) \\ 4 & \big(\frac{3}{4},\frac{5}{4}\big) \\ \hline \end{array} \nonumber\]

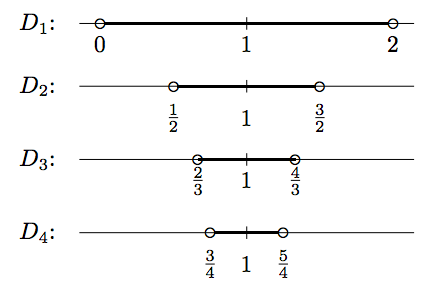
Eso es claro\(D_1\supseteq D_2 \supseteq D_3 \supseteq \cdots\,\). Así,\(\bigcup_{i=1}^\infty D_i = D_1 = (0,2)\), y\(\bigcap_{i=1}^\infty D_i = \{1\}\).

ejercicio práctico\(\PageIndex{4}\label{he:indexset-04}\)

Vamos\(E_i = \left[-i,1+\frac{1}{i}\right)\). Determinar\(\bigcup_{i=1}^\infty E_i\) y\(\bigcap_{i=1}^\infty E_i\).

Ejercicio práctico\(\PageIndex{5}\label{he:indexset-05}\)

Para cada entero positivo\(i\), defina\(F_i=\{i,i+1,i+2,\ldots,3i\}\). Determinar\(\bigcup_{i=1}^\infty F_i\) y\(\bigcap_{i=1}^\infty F_i\).

Los siguientes dos resultados son obvios.

Teorema\(\PageIndex{1}\label{subsetcap}\)

Si\(A_1 \subseteq A_2 \subseteq A_3 \subseteq \cdots\,\), entonces\(\bigcap_{i=1}^\infty A_i = A_1\).

Teorema\(\PageIndex{2}\)

Si\(A_1 \supseteq A_2 \supseteq A_3 \supseteq \cdots\), entonces\(\bigcup_{i=1}^\infty A_i = A_1\).

¿Cómo podríamos describir al sindicato\(A_2 \cup A_4 \cup A_6 \cup \cdots\,\)? Bueno, podemos escribir\[\bigcup_{i \small \, even} A_i, \nonumber\] lo que significa esa unión de\(A_i\), donde\(i\) es parejo. Dado que el conjunto de enteros pares positivos se denota por\(2\mathbb{N}\), otra forma de describir la misma unión es\[\bigcup_{i\in2\mathbb{N}} A_i. \nonumber\] Significa la unión todos\(A_i\), donde\(i\) se saca del conjunto\(2\mathbb{N}\). En consecuencia, incluso\[\bigcup_{i=0}^\infty A_i = \bigcup_{i\in\mathbb{N}} A_i, \qquad\mbox{and}\qquad \bigcap_{i=0}^\infty A_i = \bigcap_{i\in\mathbb{N}} A_i. \nonumber\] podemos ir un paso más allá,\(i\) al permitir que se tomen de cualquier conjunto de enteros, o de cualquier conjunto de números reales, o incluso de cualquier conjunto de objetos. La única restricción es que\(A_i\) debe existir, y de alguna manera su contenido debe depender de ella\(i\).

En general, dado un conjunto no vacío\(I\), si pudiéramos asociar con cada uno\(i\in I\) un conjunto\(A_i\), definimos la familia indexada de conjuntos\({\cal A}\) como\[{\cal A} = \{ A_i \mid i\in I \}. \nonumber\] Llamamos\(I\) al conjunto de índices, y definimos\[\begin{aligned} \bigcup_{i\in I} A_i &=& \{ x \mid x\in A_i \mbox{ for }some \, \, i\in I \}, \\ \bigcap_{i\in I} A_i &=& \{ x \mid x\in A_i \mbox{ for } all \, \, i\in I \}. \end{aligned} \nonumber\] Veamos algunos ejemplos.

Ejemplo\(\PageIndex{5}\label{eg:indexset-05}\)

Para describir la unión primero\[A_1\cup A_3\cup A_7\cup A_{11}\cup A_{23}, \nonumber\] definimos el conjunto de índices a ser\(I=\{1,3,7,11,23\}\), que es el conjunto de todos los subíndices utilizados en la unión. Ahora la unión puede describirse convenientemente como\(\bigcup_{i\in I} A_i\).

Ejemplo\(\PageIndex{6}\label{eg:indexset-06}\)

Considerar cinco conjuntos\[\begin{array}{r c l} A_1 &=& \{1,4,23\}, \\ A_2 &=& \{7,11,23\}, \\ A_3 &=& \{3,6,9\}, \\ A_4 &=& \{5,17,22\}, \\ A_5 &=& \{3,6,23\}. \end{array} \nonumber\] Vamos\(I=\{2,5\}\), entonces\[\bigcup_{i\in I} A_i = A_2 \cup A_5 = \{7,11,23\} \cup \{3,6,23\} = \{3,6,7,11,23\}. \nonumber\] De igual manera,\(\bigcap_{i\in I} A_i = A_2 \cap A_5 = \{7,11,23\} \cap \{3,6,23\} = \{23\}\).

Ejercicio práctico\(\PageIndex{6}\label{he:indexset-06}\)

Vamos\(J=\{1,4,5\}\). Evaluar\(\bigcup_{i\in J} A_i\) y\(\bigcap_{i\in J} A_i\), donde\(A_i\) s se definen en el último ejemplo.

Ejercicio práctico\(\PageIndex{7}\label{he:indexset-07}\)

Un conjunto de índices podría ser un conjunto de cualquier objeto. Por ejemplo, los conjuntos de números en el último ejemplo podrían ser los números favoritos de Lotto de cinco estudiantes diferentes. Podríamos indexar estos conjuntos según los nombres de los alumnos:\[\begin{array}{r c l} A_{\small John} &=& \{1,4,23\}, \\ A_{\small Mary} &=& \{7,11,23\}, \\ A_{\small Joe} &=& \{3,6,9\}, \\ A_{\small Pete} &=& \{5,17,22\}, \\ A_{\small Lucy} &=& \{3,6,23\}. \end{array} \nonumber\] Si\(I=\{\mbox{Mary},\mbox{Joe},\mbox{Lucy}\}\), ¿qué es\(\bigcup_{i\in I}\)? ¿Cómo interpretarías su significado físico?

ejemplo\(\PageIndex{7}\label{eg:indexset-07}\)

Dejar\(I = \{x\mid x \mbox{ is a living human being} \,\}\), y definir\[\begin{array}{r c l} B_i &=& \{ x \in I \mid x \mbox{ is a child of } i \}, \\ A_i &=& \{ i \} \cup B_i \end{array} \nonumber\] para cada uno\(i\in I\). Entonces\[\bigcap_{i\in I} A_i = \emptyset, \qquad \bigcup_{i\in I} A_i = I, \qquad \bigcap_{i\in I} B_i = \emptyset, \nonumber\] y lo\[\bigcup_{i\in I} B_i = I - \{ x \mid x\mbox{'s parents are both deceased}\,\}. \nonumber\] dejamos como un ejercicio para verificar estos sindicatos e intersecciones.

Ejercicio práctico\(\PageIndex{8}\label{he:indexset-08}\)

Verificar la intersección y unión en el último ejemplo.

Ejercicio de manos\(\PageIndex{9}\label{he:indexset-09}\)

Si\(I\) representa un conjunto de alumnos, y\(A_i\) representa el conjunto de amigos del estudiante\(i\), interprete el significado de\(\bigcup_{i\in I} A_i\) y\(\bigcap_{i\in I} A_i\).

Cerramos esta sección con otra generalización más de las leyes de De Morgan.

Teorema\(\PageIndex{3}\) Extended De Morgan's laws

Para cualquier conjunto de índices no vacíos\(I\), tenemos\[\overline{\bigcup_{i\in I} A_i} = \bigcap_{i\in I} \overline{A_i}, \qquad\mbox{ and }\qquad \overline{\bigcap_{i\in I} A_i} = \bigcup_{i\in I} \overline{A_i}. \nonumber\]

Prueba 1

Vamos\(x\in \overline{\bigcup_{i\in I} A_i}\), entonces\[x\notin \bigcup_{i\in I} A_i = \{ x \mid x\in A_i \mbox{ for } some \,\, i\in I \}. \nonumber\] Esto significa\(x\notin A_i\) para cada\(i\in I\). De ahí,\(x\in \overline{A_i}\) para cada uno\(i\in I\). En consecuencia,\[x\in \bigcap_{i\in I} \overline{A_i}. \nonumber\] Esto demuestra que\(\overline{\bigcup_{i\in I} A_i} \subseteq \bigcap_{i\in I} \overline{A_i}\).

A continuación, vamos\(x\in \bigcap_{i\in I} \overline{A_i}\). Entonces\(x\in \overline{A_i}\) para cada uno\(i\in I\). Esto significa\(x\notin A_i\) para cada uno\(i\in I\). Entonces\[x\notin \{ x \mid x\in A_i \mbox{ for }some \,\, i\in I \} = \bigcup_{i\in I} A_i. \nonumber\] Así,\(x\in \overline{\bigcup_{i\in I} A_i}\), demostrando eso\(\bigcap_{i\in I} \overline{A_i} \subseteq \overline{\bigcup_{i\in I} A_i}\). Ya lo probamos antes\(\overline{\bigcup_{i\in I} A_i} \subseteq \bigcap_{i\in I} \overline{A_i}\). Por lo tanto, los dos conjuntos deben ser iguales.
El comprobante de\(\overline{\bigcap_{i\in I} A_i} = \bigcup_{i\in I} \overline{A_i}\) ingresos de manera similar, y se deja como ejercicio.

Prueba 2

Vamos a probar\(\overline{\bigcup_{i\in I} A_i} = \bigcap_{i\in I} \overline{A_i}\). Te dejamos fuera las explicaciones para que las llenes:\[\begin{array}{r c l} x\in \overline{\bigcup_{i\in I} A_i} &\Leftrightarrow& \overline{x\in \bigcup_{i\in I} A_i} \\ &\Leftrightarrow& \overline{x\in A_i \mbox{ for some $i$}} \\ &\Leftrightarrow& x\notin A_i \mbox{ for all $i$} \\ &\Leftrightarrow& x\in \overline{A_i} \mbox{ for all $i$} \\ &\Leftrightarrow& x\in \bigcap_{i\in I} \overline{A_i}. \end{array} \nonumber\] La prueba de\(\overline{\bigcap_{i\in I} A_i} = \bigcup_{i\in I} \overline{A_i}\) se deja como ejercicio.

Resumen y revisión

• Al tratar con intersección arbitraria o unión de intervalos, primero identifique los puntos finales, luego analice los conjuntos involucrados en la operación para determinar si se debe incluir o excluir un punto final.
• La intersección y unión se pueden realizar en un grupo de conjuntos similares identificados por subíndices pertenecientes a un conjunto de índices.
• En consecuencia, la intersección o unión se puede formar nombrando un conjunto de índices específico.

Ejercicios 4.5

Ejercicio\(\PageIndex{1}\label{ex:indexset-01}\)

Para cada uno\(n\in\mathbb{Z}^+\), defina\(A_n=\left(-\frac{1}{n},2n\right)\). Encontrar\(\bigcap_{n=1}^\infty A_n\) y\(\bigcup_{n=1}^\infty A_n\).

Ejercicio\(\PageIndex{2}\label{ex:indexset-02}\)

Para cada uno\(n\in\mathbb{Z}^+\), defina\(B_n = \{m\in\mathbb{Z} \mid -\frac{n}{2}\leq m\leq 3n\}\). Evaluar\(\bigcap_{n=1}^\infty B_n\) y\(\bigcup_{n=1}^\infty B_n\).

Ejercicio\(\PageIndex{3}\label{ex:indexset-03}\)

Definir\(C_n=\{n,n+1,n+2,\ldots,2n+1\}\) para cada entero\(n\geq0\). Evaluar\(\bigcap_{n=0}^\infty C_n\) y\(\bigcup_{n=0}^\infty C_n\).

Ejercicio\(\PageIndex{4}\label{ex:indexset-04}\)

Para cada uno\(n\in I = \{1,2,3,\ldots,100\}\), defina\(D_n=[-n,2n]\cap\mathbb{Z}\). Evaluar\(\bigcap_{n\in I} D_n\) y\(\bigcup_{n\in I} D_n\).

Ejercicio\(\PageIndex{5}\label{ex:indexset-05}\)

Para cada uno\(n\in\mathbb{N}\), defina\(E_n = \{-n,-n+1,-n+2,\ldots,n^2\}\). Evaluar\(\bigcap_{n\in\mathbb{N}} E_n\) y\(\bigcup_{n\in\mathbb{N}} E_n\).

Ejercicio\(\PageIndex{6}\label{ex:indexset-06}\)

Para cada uno\(n\in\mathbb{N}\), defina\(F_n = \left\{\frac{m}{n} \mid m\in\mathbb{Z}\right\}\). Evaluar\(\bigcap_{n\in\mathbb{N}} F_n\) y\(\bigcup_{n\in\mathbb{N}} F_n\).

Ejercicio\(\PageIndex{7}\label{ex:indexset-07}\)

Dejar\(I=(0,1)\), y definir\(A_i = \left[1,\frac{1}{i}\right]\) para cada uno\(i\in I\). Por ejemplo\(A_{0.5} = [1,2]\) y\(A_{\frac{\pi}{4}} = \left[1,\frac{4}{\pi}\right]\). Evaluar\(\bigcup_{i\in I} A_i\) y\(\bigcap_{i\in I} A_i\).

Ejercicio\(\PageIndex{8}\label{ex:indexset-08}\)

Definir\(I=(0,1)\), y para cada uno\(i\in I\), vamos\(B_i=(-i,\frac{1}{i})\). Evaluar\(\bigcup_{i\in I} B_i = (-1,\infty)\) y\(\bigcap_{i\in I} B_i\).

Ejercicio\(\PageIndex{9}\label{ex:indexset-09}\)

Evaluar\(\bigcap_{x\in(1,2)} (1-2x,x^2)\) y\(\bigcup_{x\in(1,2)} (1-2x,x^2)\).

Ejercicio\(\PageIndex{10}\label{ex:indexset-10}\)

Evaluar\(\bigcap_{x\in(0,1)} \left(x,\frac{1}{x}\right)\) y\(\bigcup_{x\in(0,1)} \left(x,\frac{1}{x}\right)\).

Ejercicio\(\PageIndex{11}\label{ex:indexset-11}\)

Que el conjunto universal sea\(\mathbb{R}^2\). Para cada uno\(r\in(0,\infty)\), definir es\[A_r = \{(x,y)\mid y=rx^2\}; \nonumber\] decir,\(A_r\) es el conjunto de puntos sobre la parábola\(y=rx^2\), donde\(r>0\). Evaluar\(\bigcap_{r\in(0,\infty)} A_r\) y\(\bigcup_{r\in(0,\infty)} A_r\).

Ejercicio\(\PageIndex{12}\label{ex:indexset-12}\)

\( \overline{\bigcap_{i\in I} A_i} = \bigcup_{i\in I} \overline{A_i}\)Demuéstralo para cualquier conjunto de índices no vacíos\(I\).