6.1: Una introducción a las funciones

Las funciones que estudiamos en el cálculo son funciones reales, las cuales se definen sobre un conjunto de números reales, y los resultados que producen también son reales. En este capítulo, estudiaremos su generalización sobre otros conjuntos. La definición podría ser difícil de entender al principio, por lo que comenzaríamos con una breve introducción.

La mayoría de los estudiantes ven las funciones reales como dispositivos computacionales. Sin embargo, en la generalización, las funciones no se restringen únicamente a la computación. Una mejor manera de ver las funciones es su relación input-output. Dejar\(f\) denotar una función. Dado un elemento (que no necesita ser un número), llamamos al resultado de\(f\) la imagen de\(x\) debajo\(f\), y escribimos\(f(x)\), que se lee como “\(f\)de”\(x\).

Imagínese\(f\) como una máquina. Toma el valor de entrada\(x\), y devuelve\(f(x)\) como el valor de salida. Esta relación entrada-salida se representa\(\PageIndex{1}\) en la Figura de dos maneras diferentes.

Figura\(\PageIndex{1}\): Dos vistas pictóricas de una función como máquina.

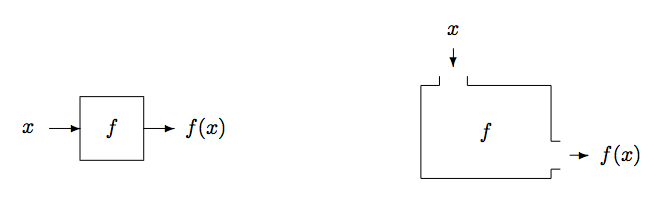
La pregunta es: ¿cómo podríamos obtener\(f(x)\)? Una función no necesita implicar ningún cálculo. En consecuencia, no podemos hablar de “computar” el valor de\(f(x)\). En cambio, hablamos de cuál es la regla que seguimos para obtener\(f(x)\). Esta regla se puede describir de muchas formas. Podemos, por supuesto, usar una regla computacional. Pero una tabla, un algoritmo, o incluso una descripción verbal también funcionan también.

Cuando decimos que una función real se define sobre los números reales, queremos decir que los valores de entrada deben ser números reales. Los valores de salida también son números reales. En general, los valores de entrada y salida no necesitan ser del mismo tipo. La función entera más cercana, denotada\([x]\), redondea el número real\(x\) al entero más cercano. Aquí, las imágenes (los valores de salida) son enteros. En consecuencia, necesitamos distinguir el conjunto de valores de entrada del conjunto de posibles valores de salida. Los llamamos el dominio y el codominio, respectivamente, de la función.

Ejemplo\(\PageIndex{1}\label{eg:fcintro-1}\)

Cuando un profesor informa las calificaciones finales de letra para los alumnos de su clase, podemos considerar esto como una función\(g\). El dominio es el conjunto de alumnos de su clase, y el codominio podría ser el conjunto de calificaciones de letras\(\{A, B, C, D, F\}\).

Dijimos que el codominio es el conjunto de posibles valores de salida, porque no todos los elementos del codominio necesitan aparecer como la imagen de algún elemento del dominio. Si ningún alumno falla la clase del profesor en el Ejemplo 6.1.1, nadie recibirá la calificación final F. La colección de las imágenes (las calificaciones finales de letras) forman un subconjunto del codominio. Llamamos a este subconjunto el rango de la función\(g\). El rango de una función puede ser un subconjunto apropiado del codominio. De ahí que el codominio de una función sea diferente del conjunto de sus imágenes. Si el rango de una función es igual al codominio, decimos que la función está en.

Ejemplo\(\PageIndex{2}\label{eg:fcintro-2}\)

Para la función entera más cercana\(h(x)=[x]\), el dominio es\(\mathbb{R}\). El codominio es\(\mathbb{Z}\), y el rango también lo es\(\mathbb{Z}\). Por lo tanto, la función entera más cercana es on.

Ejemplo\(\PageIndex{3}\label{eg:fcintro-3}\)

\(x\)Déjese ser un número real. La función mayor número entero\(\lfloor x\rfloor\) devuelve el mayor entero menor o igual a\(x\). Por ejemplo,\[\big\lfloor \sqrt{50}\,\big\rfloor = 7, \qquad \lfloor -6.34 \rfloor = -7, \qquad\mbox{and}\qquad \lfloor 15 \rfloor = 15. \nonumber\] Por lo tanto,\(\lfloor x\rfloor\) devuelve\(x\) si es un entero, de lo contrario, redondea\(x\) hacia abajo al siguiente entero más cercano. De ahí que también se le llame la función piso de\(x\). Es claro que su dominio es\(\mathbb{R}\), y el codominio y el rango son ambos\(\mathbb{Z}\).

ejercicio práctico\(\PageIndex{1}\label{he:fcintro-1}\)

\(x\)Déjese ser un número real. La función de menor número entero\(\lceil x\rceil\) devuelve el menor número entero mayor que o igual a\(x\). Por ejemplo,\[\big\lceil \sqrt{50}\,\big\rceil = 8, \qquad \lceil -6.34 \rceil = -6, \qquad\mbox{and}\qquad \lceil 15 \rceil = 15. \nonumber\] Así,\(\lceil x\rceil\) devuelve\(x\) si es un entero, de lo contrario, redondea\(x\) hasta el siguiente entero más cercano. De ahí que también se le llame la función de techo de\(x\). ¿Cuál es su dominio y codominio?

Imponemos dos restricciones a las relaciones input-output que llamamos funciones. Para cualquier valor de entrada fijo\(x\), la salida de una función debe ser la misma cada vez que usamos la función. Como máquina, escupe la misma respuesta cada vez que le damos el mismo valor\(x\). Como calculadora, muestra la misma respuesta en su pantalla cada vez que ingresamos el mismo valor\(x\), y pulsamos el botón para la función. Llamamos al valor de salida la imagen de\(x\), y escribimos\(f(x)\). El primer requisito importante para\(f\) que una función esté bien definida es: la imagen\(f(x)\) es única para cualquier\(x\) valor fijo.

Una buena máquina debe funcionar correctamente. En cuanto a una función\(f\), debemos ser capaces de obtener\(f(x)\) por cualquier valor\(x\) (y, por supuesto, producir sólo un resultado por cada uno\(x\)). Esto quizás sea un poco demasiado exigente. Un remedio es restringir nuestra atención a aquellos sobre\(x\) los que\(f\) funcionarían. El conjunto de valores de entrada legítimos es precisamente lo que llamamos el dominio de la función. En consecuencia, el segundo requisito dice: para cada elemento\(x\) del dominio, el valor de salida\(f(x)\) debe estar bien definido. Esta es la forma matemática de decir que se\(f(x)\) puede obtener el valor.

Ejemplo\(\PageIndex{4}\label{eg:fcintro-4}\)

Compare esto con una calculadora. Si ingresa un número negativo y presiona el\(\sqrt{\phantom{x}}\,\) botón, aparecerá un mensaje de error. Para poder calcular la raíz cuadrada de un número, el número debe ser no negativo. El dominio de una función es el conjunto de valores de entrada aceptables para los que se pueden encontrar resultados significativos. Para la función raíz cuadrada, el dominio es\(\mathbb{R}^+\cup\{0\}\), que es el conjunto de números reales no negativos.

ejercicio práctico\(\PageIndex{2}\label{he:fcintro-2}\)

Para la función raíz cuadrada, podemos considerar su codominio como\(\mathbb{R}\). ¿Cuál es su alcance? ¿La función está en?

ejercicio práctico\(\PageIndex{3}\label{he:fcintro-3}\)

Para la función raíz cuadrada, ¿podemos decir que su dominio es\(\mathbb{R}^+\cup0\)? Explique.

Las dos condiciones para que una función esté bien definida a menudo se combinan y escriben como si se tratara de una sola condición:

Una función\(f\) está bien definida si cada elemento\(x\) del dominio tiene una imagen única en el codominio.

Cuando examine esta definición más de cerca, encontrará los dos requisitos separados:

• cada elemento del dominio tiene una imagen debajo\(f\), y
• la imagen es única.

En la siguiente sección, presentaremos la definición formal completa.

Resumen y revisión

• Una función es una regla que asigna a cada elemento del dominio una imagen única en el codominio.

ejercicio\(\PageIndex{1}\label{ex:fcintro-1}\)

Complete la siguiente tabla:

\[ \begin{array}{|c||c|c|c|c|c|c|} \hline x & 5.7 & \pi & e & -7.2 & -0.8 & 9 \\ \hline \lfloor x \rfloor & \qquad\qquad & \qquad\qquad & \qquad\qquad & \qquad\qquad & \qquad\qquad & \qquad\qquad \\ \lceil x \rceil &&&&&& \\ {[x]} &&&&&& \\ \hline \end{array} \nonumber\]

ejercicio\(\PageIndex{2}\label{ex:fcintro-2}\)

¿Cuál es el dominio y el codominio de la función de raíz cubo? ¿Está sobre?

ejercicio\(\PageIndex{3}\label{ex:fcintro-3}\)

Para la función raíz cuadrada, ¿cómo usarías la notación de intervalo para describir el dominio?

ejercicio\(\PageIndex{4}\label{ex:fcintro-4}\)

Para la función raíz cuadrada, ¿qué complemento de conjunto usarías para describir el dominio?