6.2: Definición de Funciones

Última actualización
Guardar como PDF

Page ID: 112976

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Definición

Dejar$A$ y$B$ ser conjuntos no vacíos. Una función de$A$ a$B$ es una regla que asigna a cada elemento de$A$ un elemento único en$B$. Llamamos$A$ al dominio, y$B$ al codominio, de la función. Si se llama a la función$f$, escribimos$f :A \to B$. Dado$x\in A$, su elemento asociado en$B$ se llama su imagen bajo$f$. Lo denotamos$f(x)$, que se pronuncia como “$f$de”$x$.

Una función a veces se llama mapa o mapeo. De ahí que a veces le digamos$f$ mapas$x$ a su imagen$f(x)$. Las funciones también se llaman transformaciones.

Ejemplo$\PageIndex{1}\label{eg:defnfcn-01}$

La función$f:\{a,b,c\} \to \{1,3,5,9\}$ se define de acuerdo a la regla\[f(a)=1, \qquad f(b)=5, \qquad\mbox{and}\qquad f(c) = 9. \nonumber\] Es una función bien definida. La regla de asignación se puede resumir en una tabla: También\[\begin{array}{|c||c|c|c|} \hline x & a & b & c \\ \hline f(x)& 1 & 5 & 9 \\ \hline \end{array} \nonumber\] podemos describir la regla de asignación pictóricamente con un diagrama de flechas, como se muestra en la Figura$\PageIndex{1}$.

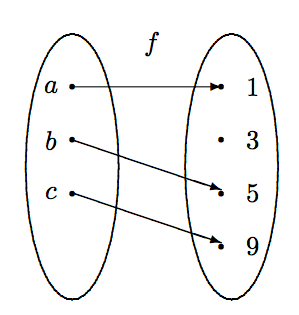
Screen Shot 2020-01-13 at 10.31.42 AM.png — Figura$\PageIndex{1}$: Un ejemplo de una función bien definida.

Los dos requisitos clave de una función son

cada elemento del dominio tiene una imagen debajo$f$, y
la imagen es única.

Es posible que desee recordar que cada elemento en$A$ tiene exactamente un “socio” en$B$.

Ejemplo$\PageIndex{2}\label{eg:defnfcn-02}$

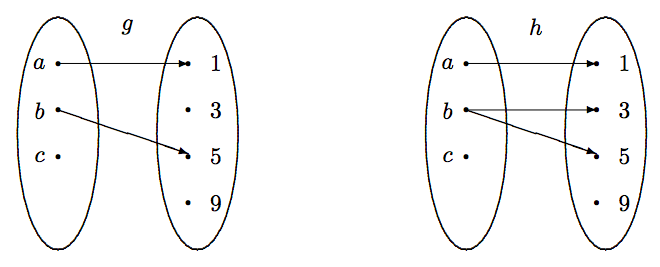
La figura$\PageIndex{2}$ representa dos ejemplos de no funciones. En el de la izquierda, uno de los elementos del dominio no tiene ninguna imagen asociada a él. En el de la derecha, uno de los elementos del dominio tiene dos imágenes asignadas al mismo. Ambas no son funciones.

Screen Shot 2020-01-13 a las 10.33.33 AM.png — Figura$\PageIndex{2}$: Dos tipos de no funciones.

ejercicio práctico$\PageIndex{1}\label{he:defnfcn-01}$

¿Estas reglas\[\begin{array}{|c||c|c|c|} \hline x & a & b & c \\ \hline f(x)& 5 & 3 & 3 \\ \hline \end{array} \hskip0.75in \begin{array}{|c||c|c|} \hline x & b & c \\ \hline g(x)& 9 & 5 \\ \hline \end{array} \hskip0.75in \begin{array}{|c||c|c|c|c|} \hline x & a & b & b & c \\ \hline h(x)& 1 & 5 & 3 & 9 \\ \hline \end{array} \nonumber\] producen funciones bien definidas desde$\{a,b,c\}$ hasta$\{1,3,5,9\}$? Explique.

ejercicio práctico$\PageIndex{2}\label{he:defnfcn-02}$

¿La definición\[r(x) = \cases{ x & if today is Monday, \cr 2x & if today is not Monday \cr} \nonumber\] produce una función bien definida de$\mathbb{R}$ a$\mathbb{R}$? Explique.

ejercicio práctico$\PageIndex{3}\label{he:defnfcn-03}$

¿La definición\[s(x) = \cases{ 5 & if $x<2$, \cr 7 & if $x>3$, \cr} \nonumber\] produce una función bien definida de$\mathbb{R}$ a$\mathbb{R}$? Explique.

Ejemplo$\PageIndex{3}\label{eg:defnfcn-03}$

La función$f:{[0,\infty)}\to{\mathbb{R}}$ definida por\[f(x) = \sqrt{x} \nonumber\] está bien definida. Entonces se${g}:{[2,\infty)}\to{\mathbb{R}}$ define la función como ¿\[g(x) = \sqrt{x-2}. \nonumber\]Puedes explicar por qué es el dominio$[2,\infty)$?

Ejemplo$\PageIndex{4}\label{eg:defnfcn-04}$

Vamos a$A$ denotar el conjunto de alumnos que toman Matemáticas Discretas$G=\{A,B,C,D,F\}$, y, y$\ell(x)$ es la calificación final de estudiante$x$ en Matemáticas Discretas. Todo estudiante debe recibir una calificación final, y el instructor tiene que reportar una y sólo una calificación final por cada alumno. Esto es precisamente lo que llamamos una función.

Ejemplo$\PageIndex{5}\label{eg:defnfcn-05}$

La función${n}:{\wp(\{a,b,c,d\})}\to{\mathbb{Z}}$ se define como$n(S)=|S|$. Evalúa la cardinalidad de un subconjunto de$\{a,b,c,d\}$. Por ejemplo,\[n\big(\{a,c\}\big) = n\big(\{b,d\}\big) = 2. \nonumber\] Tenga en cuenta que$n(\emptyset)=0$.

ejercicio práctico$\PageIndex{4}\label{he:defnfcn-04}$

Considere el Ejemplo 6.2.5. ¿Qué otros subconjuntos$S$ de$\{a,b,c,d\}$ también rinden$n(S)=2$? ¿Cuáles son las imágenes más pequeñas y más grandes que$n$ puede producir la función?

Ejemplo$\PageIndex{6}\label{eg:defnfcn-06}$

Considera una función${f}:{\mathbb{Z}_7}\to{\mathbb{Z}_5}$. El dominio y el codominio son,

\[\mathbb{Z}_7 = \{0,1,2,3,4,5,6\}, \qquad\mbox{and}\qquad \mathbb{Z}_5 = \{0,1,2,3,4\}, \nonumber\]

respectivamente. No sólo sus elementos son diferentes, sus operaciones binarias también son diferentes. En el dominio$\mathbb{Z}_7$, la aritmética se realiza módulo 7, pero la aritmética en el codominio$\mathbb{Z}_5$ se realiza módulo 5. Por lo tanto, debemos tener cuidado al describir la regla de asignación si se trata de un cómputo. Podríamos decir, por ejemplo,

\[f(x) = z, \quad\mbox{where } z \equiv 3x \pmod{5}. \nonumber\]

En consecuencia, comenzando con cualquier elemento$x$ en$\mathbb{Z}_7$, consideramos$x$ como un entero ordinario, multiplicamos por 3, y reducimos la respuesta módulo 5 para obtener la imagen$f(x)$. Por brevedad, escribiremos

\[f(x) \equiv 3x \pmod{5}. \nonumber\]

Resumimos las imágenes en la siguiente tabla:

\[\begin{array}{|c||*{7}{c|}} \hline n & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline f(n) & 0 & 3 & 1 & 4 & 2 & 0 & 3 \\ \hline \end{array} \nonumber\]

Toma nota de que las imágenes empiezan a repetirse después$f(4)=2$.

ejercicio práctico$\PageIndex{5}\label{he:defnfcn-05}$

Tabular las imágenes de${g}:{\mathbb{Z}_{10}}\to{\mathbb{Z}_5}$ definido por\[g(x) \equiv 3x \pmod{5}. \nonumber\]

Definición

La gráfica de una función${f}:{A}\to{B}$ es el conjunto de pares ordenados$(x,y)$ de$A\times B$ tal manera que$y=f(x)$.

La gráfica de una función, en esta definición general, puede no parecerse al tipo de gráficas que esperábamos de funciones reales. Una gráfica es, por definición, un conjunto de pares ordenados.

Ejemplo$\PageIndex{7}\label{eg:defnfcn-07}$

El gráfico de la función$f$ en el Ejemplo 6.2.6 es el conjunto de pares ordenados\[\{(0,0), (1,3), (2,1), (3,4), (4,2), (5,0), (6,3)\}. \nonumber\] Si uno insiste, podríamos mostrar la gráfica de una función usando un$xy$ -plano que se asemeja al plano cartesiano habitual. Tenga en cuenta: los elementos$x$ y$y$ provienen de$A$ y$B$, respectivamente. Podemos “trazar” la gráfica para$f$ en el Ejemplo 6.2.6 como se muestra a continuación.

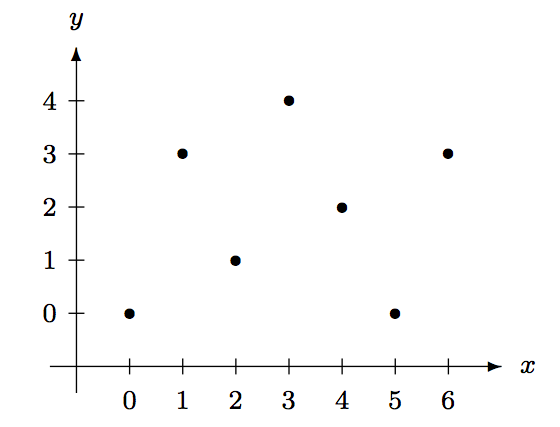
Screen Shot 2020-01-13 a las 10.39.58 AM.png

Además de usar una representación gráfica, también podemos usar una$(0,1)$ -matrix. A$(0,1)$ -matrix es una matriz cuyas entradas son 0 y 1. Para la función$f$, usamos una$7\times5$ matriz, cuyas filas y columnas corresponden a los elementos de$A$ y$B$, respectivamente, y ponemos uno en la entrada$(i,j)$ th si$j=f(i)$, y cero en caso contrario. La matriz resultante es

\[\begin{array}{cc} & \begin{array}{ccccc} 0 & 1 & 2 & 3 & 4 \end{array} \\ \begin{array}{c} 0 \\ 1 \\ 2 \\ 3 \\ 4 \\ 5 \\ 6 \end{array} & \left(\begin{array}{ccccc} 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{array}\right) \end{array} \nonumber\]

Lo llamamos la matriz de incidencia para la función$f$.

ejercicio práctico$\PageIndex{6}\label{he:defnfcn-06}$

“Trazar” la gráfica de$g$ en Ejercicio Práctico 6.2.5. También construir su matriz de incidencia.

Resumen y revisión

Una función$f$ de un conjunto$A$ a un conjunto$B$ (llamada dominio y codominio, respectivamente) es una regla que describe cómo$B$ se asigna un valor en el codominio a un elemento del dominio$A$.
Pero no es una regla cualquiera; más bien, la regla debe asignar a cada elemento$x$ del dominio un valor único en el codominio.
Este valor único se llama la imagen de$x$ debajo de la función$f$, y se denota$f(x)$.
Usamos la notación${f}:{A}\to{B}$ para indicar que el nombre de la función es$f$, el dominio es$A$, y el codominio es$B$.
La gráfica de una función${f}:{A}\to{B}$ es la colección de todos los pares ordenados$(x,y)$ de$A\times B$ tal manera que$y=f(x)$.
La gráfica de una función puede no ser una curva, como en el caso de una función real. Puede ser solo una colección de puntos.
También podemos mostrar las imágenes de una función en una tabla, o representar la función con una matriz de incidencia.

ejercicio$\PageIndex{1}\label{ex:defnfcn-01}$

¿Qué$A$ subconjunto$\mathbb{R}$ usarías para hacer${f}:{A}\to{\mathbb{R}}$ definido por$f(x) = \sqrt{3x-7}$ una función bien definida?

ejercicio$\PageIndex{2}\label{ex:defnfcn-02}$

¿Qué$A$ subconjunto$\mathbb{R}$ usarías para hacer

${g}:{A}\to{\mathbb{R}}$, donde$g(x) = \sqrt{(x-3)(x-7)}$
${h}:{A}\to{\mathbb{R}}$, donde$h(x) = \frac{x+2}{\sqrt{(x-2)(5-x)}}$

funciones bien definidas?

ejercicio$\PageIndex{3}\label{ex:defnfcn-03}$

¿Cuál de estos datos soporta una función bien definida de$\{1,2,3,4\}$ a$\{1,2,3,4\}$? Explique.

\[\begin{array}{|c||c|c|c|} \hline x & 1 & 2 & 3 \\ \hline f(x) & 3 & 4 & 2 \\ \hline \end{array} \hskip0.4in \begin{array}{|c||c|c|c|c|} \hline x & 1 & 2 & 3 & 4 \\ \hline g(x) & 2 & 4 & 3 & 2 \\ \hline \end{array} \hskip0.4in \begin{array}{|c||c|c|c|c|c|} \hline x & 1 & 2 & 3 & 3 & 4 \\ \hline h(x) & 2 & 4 & 3 & 2 & 3 \\ \hline \end{array} \nonumber\]

ejercicio$\PageIndex{4}\label{ex:defnfcn-04}$

¿Cuáles de las siguientes son la representación gráfica o matriz de incidencia de funciones bien definidas de$\{1,2,3,4\}$ a$\{1,2,3,4\}$? Explique.

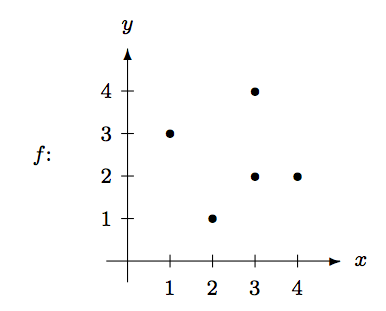
Screen Shot 2020-01-13 a las 10.42.46 AM.png

\[g: ~ \begin{array}[t]{cc} & \begin{array}{cccc} 1 & 2 & 3 & 4 \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \end{array} & \left(\begin{array}{cccc} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right) \end{array} \nonumber\]

ejercicio$\PageIndex{5}\label{ex:defnfcn-05}$

Determinar si se trata de funciones bien definidas. Explique.

${f}:{\mathbb{R}}\to{\mathbb{R}}$, donde$f(x) = \frac{3}{x^2+5}$.
${g}:{(5,\infty)}\to{\mathbb{R}}$, donde$g(x) = \frac{7}{\sqrt{x-4}}$.
${h}:{\mathbb{R}}\to{\mathbb{R}}$, donde$h(x) = -\sqrt{7-4x+4x^2}$.

ejercicio$\PageIndex{6}\label{ex:defnfcn-06}$

Determinar si se trata de funciones bien definidas. Explique.

${s}:{\mathbb{R}}\to{\mathbb{R}}$, donde$ x^2+[s(x)]^2=9$.
${t}:{\mathbb{R}}\to{\mathbb{R}}$, donde$|x-t(x)|=4$.

ejercicio$\PageIndex{7}\label{ex:defnfcn-07}$

A continuación se muestra la gráfica de la función$p$ y la matriz de incidencia para la función$q$, respectivamente, de$\{1,2,3,4\}$ a$\{1,2,3,4\}$.

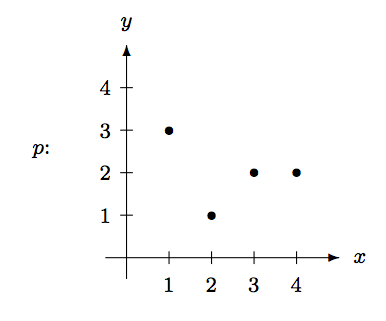
Screen Shot 2020-01-13 at 10.44.02 AM.png

\[q: ~ \begin{array}[t]{cc} & \begin{array}{cccc} 1 & 2 & 3 & 4 \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \end{array} & \left(\begin{array}{cccc} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{array}\right) \end{array} \nonumber\]

Complete la siguiente tabla:\[\begin{array}{|c||c|c|c|c|} \hline x & 1 & 2 & 3 & 4 \\ \hline p(x) & \qquad & \qquad & \qquad & \qquad \\ \hline \end{array} \hskip0.4in \begin{array}{|c||c|c|c|c|} \hline x & 1 & 2 & 3 & 4 \\ \hline q(x) & \qquad & \qquad & \qquad & \qquad \\ \hline \end{array} \nonumber\]

ejercicio$\PageIndex{8}\label{ex:defnfcn-08}$

Deja$T$ ser tu árbol genealógico que incluye a tu madre biológica, tu abuela materna, tu bisabuela materna, etc., y todas sus descendientes femeninas. Determinar cuál de los siguientes define una función de$T$ a$T$.

${h_1}:{T}\to{T}$, donde$h_1(x)$ esta la madre de$x$.
${h_2}:{T}\to{T}$, donde$h_2(x)$ está$x$ la hermana.
${h_3}:{T}\to{T}$, donde$h_3(x)$ es una tía de$x$.
${h_4}:{T}\to{T}$, donde$h_4(x)$ está la hija mayor de$x$ la abuela materna.

ejercicio$\PageIndex{9}\label{ex:defnfcn-09}$

Para cada una de las siguientes funciones, determinar la imagen del dado$x$.

${k_1}:{\mathbb{N}-\{1\}}\to{\mathbb{N}}$,$k_1(x)=\text{smallest prime factor of }x, ~ x=217$.
${k_2}:{\mathbb{Z}_{11}}\to{\mathbb{Z}_{11}}$,$k_2(x)\equiv3x$ (mod 11),$x=6$.
${k_3}:{\mathbb{Z}_{15}}\to{\mathbb{Z}_{15}}$,$k_3(x)\equiv3x$ (mod 15),$x=6$.

ejercicio$\PageIndex{10}\label{ex:defnfcn-10}$

Para cada una de las siguientes funciones, determine las imágenes de los$x$ valores -dados.

${\ell_1}:{\mathbb{Z}}\to{\mathbb{Z}}$,$\ell_1(x)=x\bmod7$$x=250$,$x=0$, y$x=-16$.

Observación: Recordemos que, sin paréntesis, la notación “mod” significa el mod de operación binaria.

${\ell_2}:{\mathbb{Z}}\to{\mathbb{Z}}$,$\ell_2(x)=\gcd(x,24)$$x=100$,$x=0$, y$x=-21$.