1.8: Geometría de números

Ya hemos visto que los conceptos geométricos a veces son útiles para iluminar consideraciones teóricas numéricas. Con la introducción por Minkowski de la geometría de los números se logró una soldadura real de partes importantes de la teoría de números y la geometría. Esta rama de las matemáticas ha estado en boga considerable en los últimos 20 años, particularmente en Inglaterra donde fue y está siendo desarrollada vigorosamente por Mordell, Davenport, Mahler y sus alumnos.

Consideraremos una introducción muy breve sobre este tema. Primero, examinaremos una prueba del teorema fundamental de Minkowski debido a Hajos (1934), luego discutiremos algunas generalizaciones y aplicaciones de este teorema, y finalmente investigaremos algunos nuevos resultados y conjeturas que están estrechamente relacionadas.

En su forma más simple el teorema fundamental de Minkowski es el siguiente.

Teorema\(\PageIndex{1}\): Fundamental Theorem of Minkowski

Dejar\(R\) ser una región en el\(x-y\) plano de área\(A > 4\), simétrica sobre el origen y convexa. Entonces\(R\) contiene un punto de celosía distinto del origen.

En primer lugar, algunas observaciones preliminares. En la condición\(A > 4\), el 4 no puede ser reemplazado por ningún número menor. Esto puede verse considerando el cuadrado de lado\(2 − \epsilon\), centrado en el origen. En efecto, este ejemplo podría sugerir al principio que el teorema es bastante intuitivo, ya que podría parecer que apretar esta región en cualquier dirección y mantener su área fija forzaría necesariamente a la región a cubrir algún punto de celosía. Sin embargo el asunto no es tan sencillo, ya que otros ejemplos revelan que ni la simetría central ni la convexidad son indispensables. En lo que respecta a la convexidad lo que realmente se necesita es que con los vectores\(\vec{V_1}\) y\(\vec{V_2}\) la región también se debe contener\(\dfrac{1}{2} (\vec{V_1} + \vec{V_2})\). La simetría significa que con\(\vec{V_1}\) el vector también\(-\vec{V_1}\) debe estar en\(R\). Así, la simetría y convexidad juntas implican que, si\(\vec{V_1}\) y\(\vec{V_2}\) están en\(R\), así es\(\dfrac{1}{2} (\vec{V_1} - \vec{V_2})\). Esta última condición es realmente suficiente para nuestro propósito y puede reemplazar las condiciones de simetría y convexidad. Está implícita por la simetría y la convexidad pero no implica ninguna de estas condiciones.

Otro ejemplo que quizás ilumina el significado del teorema de Minkowski es el siguiente. Considera una línea a través de\(O\) tener pendiente irracional\(\tan \theta\); ver Figura 4. Esta línea no pasa por ningún punto de celosía que no sea el origen. Si tomamos un segmento largo de esta línea, digamos extendiendo la longitud a cada\(R\) lado de\(O\), entonces habrá un punto de celosía más cercano a, y una\(r\) distancia de,

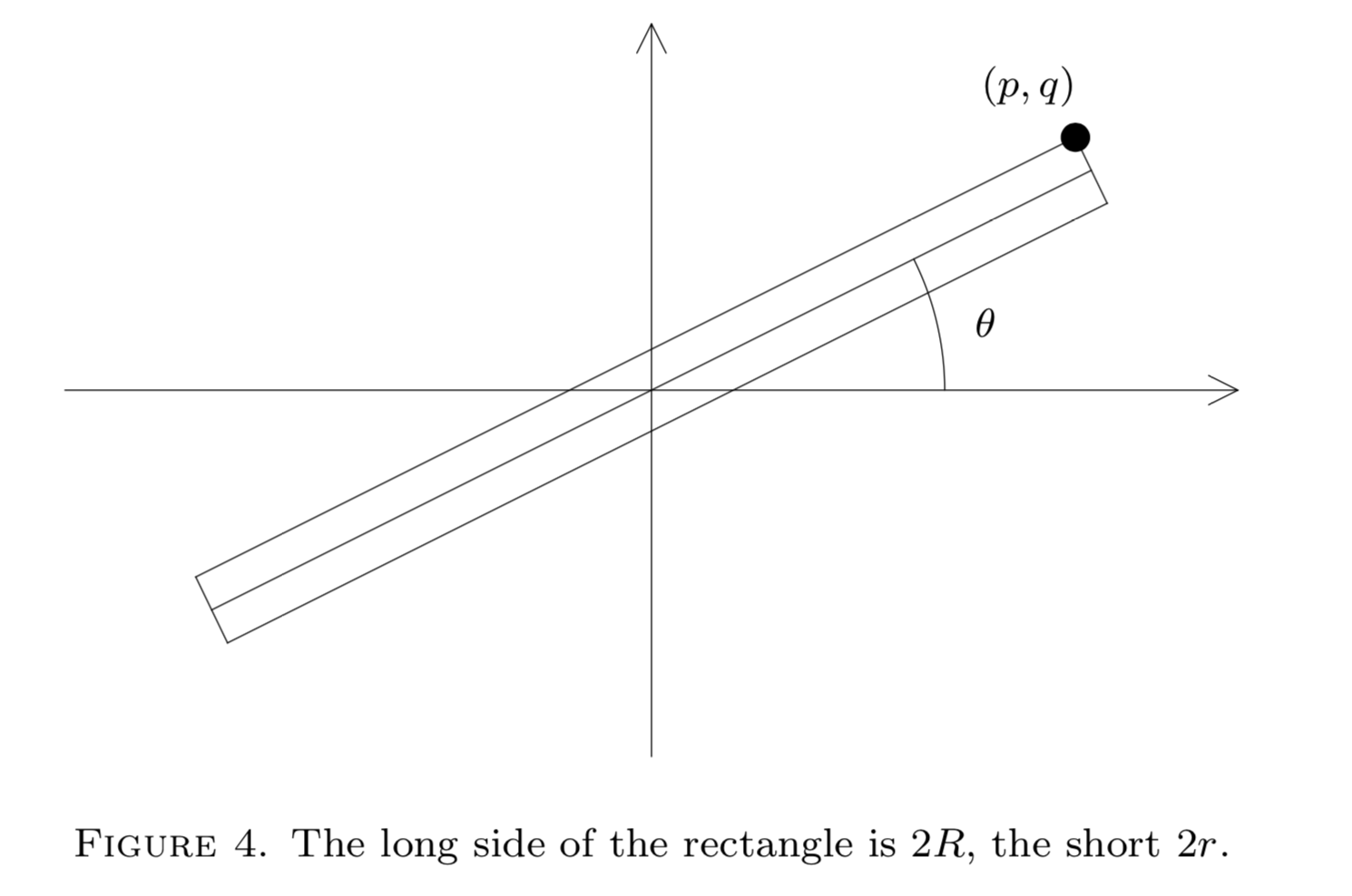
este segmento. De ahí que, no importa cuán grande\(R\) sea, podemos construir un rectángulo que contenga este segmento de línea, que no contenga otro punto de celosía que no sea\(O\). Por el teorema fundamental de Minkowski el área\(4rR\) de este rectángulo no supera 4. Así\(r \le \dfrac{1}{R}\). Obsérvese que si\((p, q)\) es un punto de celosía en el borde del rectángulo entonces\(\dfrac{p}{q} \approx \tan \theta\), de manera que el teorema fundamental de Minkowski dará alguna información sobre lo cerca que un número irracional puede ser aproximado por los racionales.

Volvamos ahora a Hajos prueba del teorema fundamental de Minkowski. Considera el\(x-y\) plano cortado en un tablero de ajedrez infinito con el cuadrado básico del área 4 determinado por\(|x| \le 1\),\(|y| \le 1\). Ahora cortamos el tablero de ajedrez a lo largo de los bordes de los cuadrados y superponemos todos los cuadrados que contienen partes de la región\(R\). Ahora hemos comprimido un área > 4 en una región del área 4. Esto implica que habrá algún solapamiento, es decir, se puede pegar un alfiler a través del cuadrado para perforar\(R\) en dos puntos digamos\(V_1\) y\(V_2\). Ahora reensamblar la región y dejar que los puntos\(V_1\) y\(V_2\) sean los vectores\(\vec{V_1}\) y\(\vec{V_2}\). Considera el hecho de que las\(y\) coordenadas\(x\) y de\(V_1\) y\(V_2\) difieren en un múltiplo de 2. Escribimos\(V_1 \equiv V_2\) (mod 2), lo que implica\(\dfrac{1}{2} (V_1 - V2) \equiv 0\) (mod 1). Así\(\dfrac{1}{2} (V_1 - V_2)\) es un punto de celosía diferente de O (ya que\(V_1 \ne V_2\)) en\(R\).

El teorema fundamental de Minkowski puede generalizarse fácilmente al espacio\(n\) -dimensional. De hecho solo necesitamos reemplazar 4 en el teorema fundamental de Minkowski por 2n y la prueba de Hajos pasa por. Se han dado muchas extensiones y mejoras del teorema fundamental de Minkowski. Volveré a algunas de ellas más tarde.

Uno de los primeros trabajos de Polya tiene el largo y curioso título “Zahlhlentheoretisches und Wahrscheinlichkeitstheoretisches\(\ddot{u}\) ber die Sichtweite in Walde und durch Schneefall”. Una prueba del resultado principal de Polya en este trabajo puede simplificarse en gran medida y refinarse utilizando el teorema fundamental de Minkowski. El problema es este.

Supongamos que cada punto de celosía que no sea\(O\) está rodeado por un círculo de radio\(r \le \dfrac{1}{2}\) (un árbol en un bosque). Un hombre se para en\(O\). En dirección\(\theta\) puede ver una distancia\(f(r, \theta)\). distancia f (r, θ). ¿Qué es lo más lejos que puede ver en cualquier dirección? Es decir, determinar

\(F(r) = \text{max}_{\theta} f(\theta, r)\)

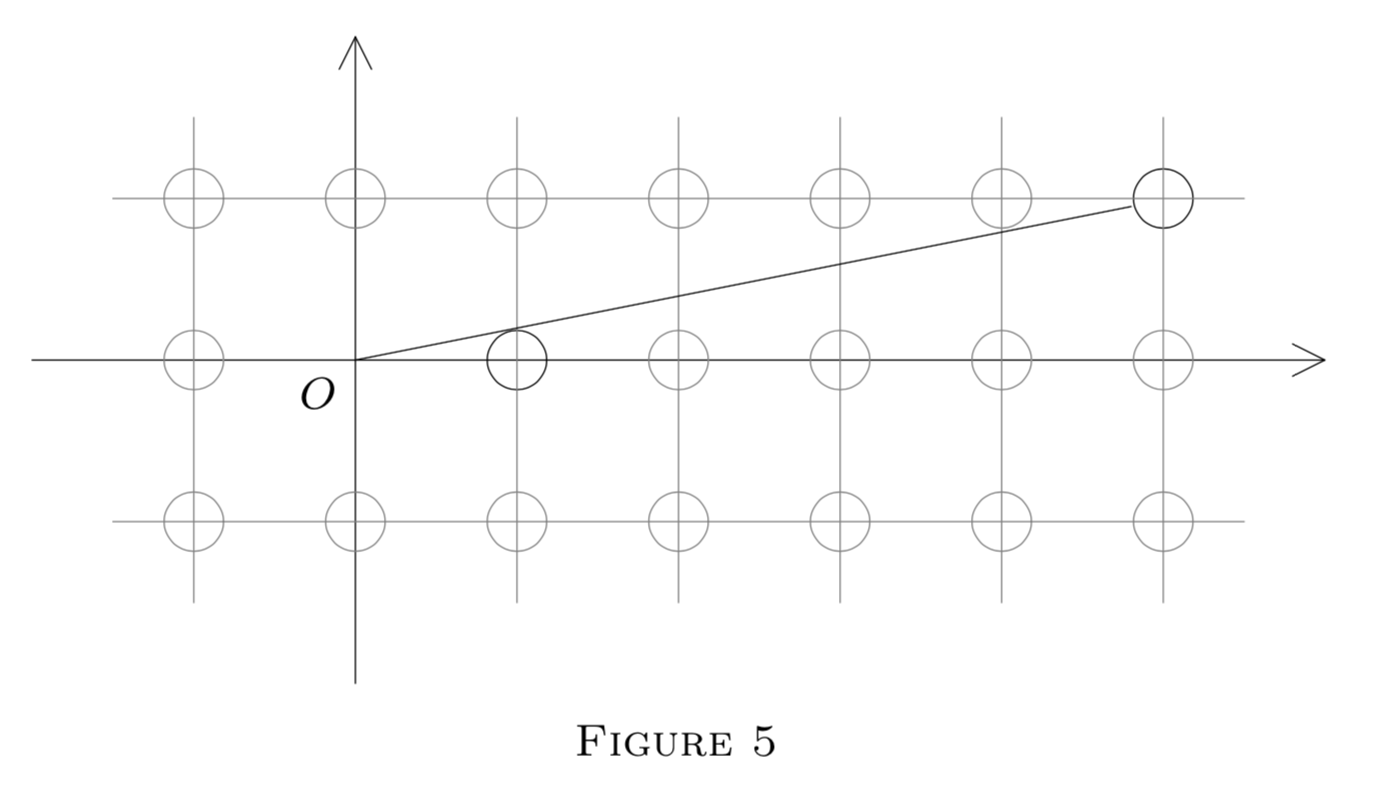
Al mirar más allá del círculo centrado en (1, 0) (Figura 5), podemos ver casi una distancia\(\dfrac{1}{r}\). Por otro lado podemos demostrarlo\(F(r) \le \dfrac{1}{r}\). Por supongamos que podemos ver una distancia\(F(r)\) en dirección θ. Acerca de esta línea de visión construir un rectángulo con lado\(2r\). Este rectángulo no contiene ningún punto de celosía, ya que de lo contrario el árbol centrado en dicho punto de celosía obstruiría nuestra línea de visión; ver Figura 6.

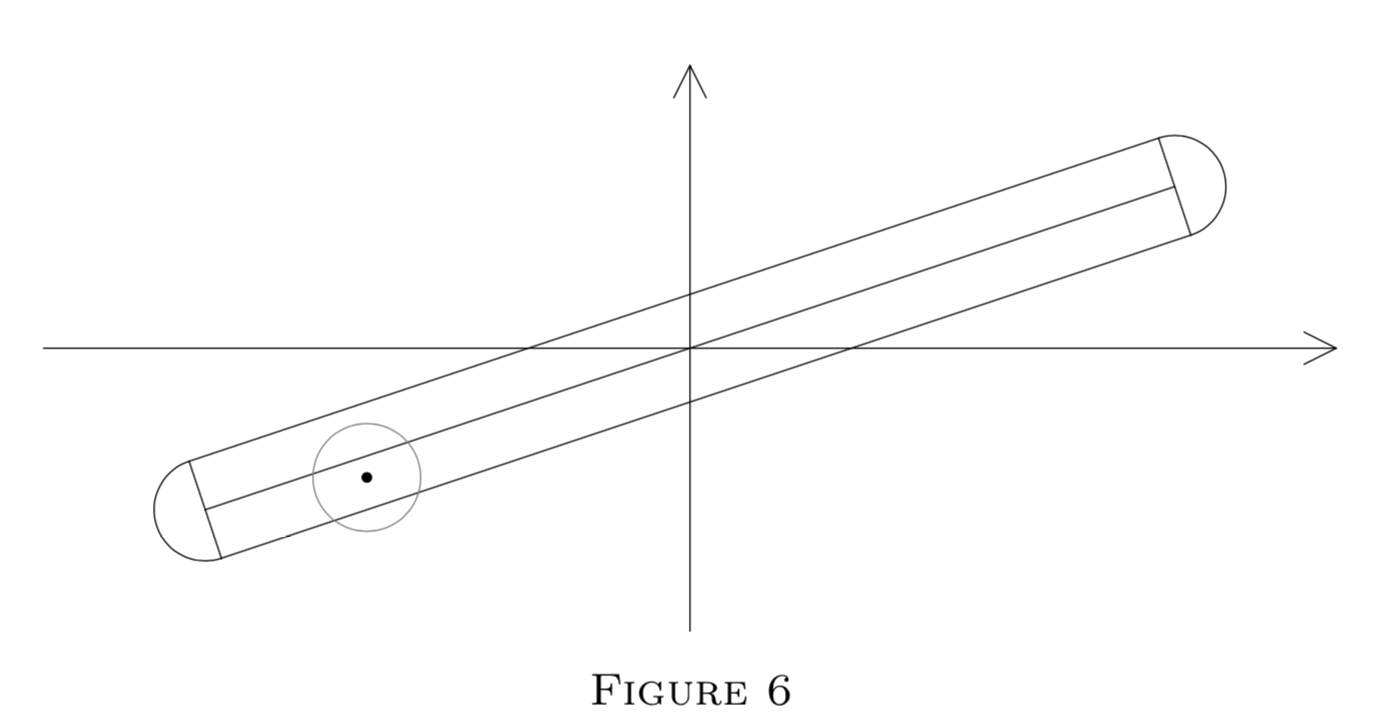
De ahí, por el teorema fundamental de Minkowski\(4F(r) r \le 4\) y\(F(r) \le \dfrac{1}{r}\) como se requiera. Tenga en cuenta que ningún punto de celosía puede estar en ninguno de los semicírculos del diagrama. Esto nos permite mejorar ligeramente el resultado de Polya. Dejaré los detalles como ejercicio.

Una aplicación más significativa del teorema fundamental de Minkowski se refiere a la posibilidad de resolver en enteros un conjunto de desigualdades lineales.

Considerar las desigualdades

\(|a_{11} x_{1} + a_{12}x_{2} + \cdot\cdot\cdot + a_{1n}x_{n}| \le \lambda_1,\)
\(|a_{21} x_{1} + a_{22}x_{2} + \cdot\cdot\cdot + a_{2n}x_{n}| \le \lambda_2,\)
.
.
.
\(|a_{n1} x_{1} + a_{n2}x_{2} + \cdot\cdot\cdot + a_{nn}x_{n}| \le \lambda_n,\)

donde\(a_{ij}\) son números reales y los\(\lambda_1, \lambda_2, ..., \lambda_n\) son números positivos. El problema es encontrar condiciones suficientes para la existencia de enteros\(x_1, ..., x_n\), no todos 0 satisfaciendo el sistema. El teorema fundamental de Minkowski puede ser utilizado para demostrar que existirá una solución siempre que el determinante det (aij) de los coeficientes sea, en valor absoluto, menor que el producto\(\lambda_1 \cdot \lambda_2 \cdot\cdot\cdot\cdot\cdot \lambda_n\). Esto se produce de la siguiente manera. Geométricamente, las desigualdades determinan un paralelepípedo\(n\) −dimensional cuyo volumen (o contenido) es

\(\dfrac{1}{\text{det} (a_{ij})} \cdot 2^n \cdot \lambda_1 \cdot \lambda_2 \cdot\cdot\cdot\cdot\cdot \lambda_n.\)

Si\(\lambda_1 \cdot \lambda_2 \cdot\cdot\cdot\cdot\cdot \lambda_n > \text{det} (a_{ij})\) entonces el contenido excede\(2^n\) y así contiene un punto de celosía diferente de\(O\).

Un análogo muy reciente del teorema fundamental de Minkowski es el siguiente. Dejar\(R\) ser una región convexa, no necesariamente simétrica sobre O, sino que tiene su centroide en\(O\). Si su área excede\(\dfrac{9}{2}\), entonces contiene un punto de celosía no\(O\). La constante\(\dfrac{9}{2}\) vuelve a ser lo mejor posible, pero se desconoce un análogo n-dimensional de este resultado.

A continuación se presenta una generalización conjeturada del teorema fundamental de Minkowski, que lamentablemente no hemos podido probar. A lo mejor podrás probarlo o desmentirlo. Dejar\(R\) ser una región convexa que contiene el origen y definida por\(r = f(\theta)\),\(0 \le \theta < 2 \pi\). Si

\(\int_0^{\pi} f(\theta) f(\theta + \pi) d \theta > 4\)

luego\(R\) contiene un punto de celosía no trivial. Para regiones simétricas\(f(\theta) = f(\theta + \pi)\), y la conjetura se reduce al teorema fundamental de Minkowski.

Aquí hay un problema algo relacionado y sólo parcialmente resuelto. \(M(n)\)Sea definido como el número más pequeño tal que cualquier región convexa del área se\(M(n)\) pueda colocar de manera que cubra los puntos de\(n\) celosía. Claramente\(M(1) = 0\). No es difícil demostrar que\(M(2) = \dfrac{\pi}{4}\), es decir, cualquier región convexa cuya área supere la de un círculo de diámetro 1 puede ser utilizada para cubrir 2 puntos de celosía. Determinar\(M(3)\) ya parece difícil. Lo que uno puede probar fácilmente es eso\(M(n) \le n -1\) y conjeturamos la existencia de una constante positiva\(c\) tal que\(M(n) < n - c \sqrt{n}\).