1.1: Divisores y Congruencias

Última actualización
Guardar como PDF

Page ID: 111516

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Definición 1.1

Dados dos números$a$ y$b$. Un múltiplo$b$ de$a$ es un número que satisface$b = ac$. Un divisor$a$ de$b$ es un entero que satisface$ac = b$ donde$c$ es un entero. Escribimos$a|b$. Esto se lee como$a$ divide$b$ o un es$a$ divisor de$b$.

Definición 1.2

Dejar$a$ y$b$ no cero. El mayor común divisor de dos enteros$a$ y$b$ es el máximo de los números que son divisores de ambos$a$ y$b$. Se denota por$\gcd(a, b)$. El múltiplo menos común de$a$ y$b$ es el menor de los números positivos que son múltiplos de ambos$a$ y$b$. Se denota por$\mbox{lcm}(a ,b)$.

Tenga en cuenta que para cualquiera$a$ y$b$ en$\mathbb{Z}$$\gcd(a, b) \ge 1$,, como 1 es un divisor de cada entero. De igual manera$\mbox{lcm} (a, b) \le |ab|$.

Definición 1.3

Un número$a > 1$ es primo en$\mathbb{N}$ si sus únicos divisores en$\mathbb{N}$ son$a$ y 1 (los llamados divisores triviales). Un número$a > 1$ es compuesto si tiene más de 2 divisores. (El número 1 no es ninguno.)

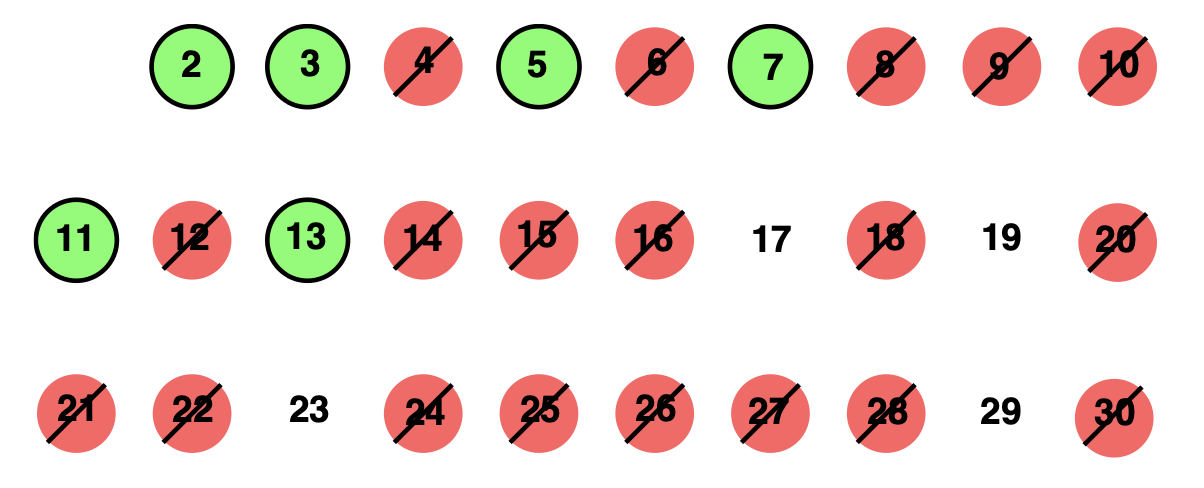
$Screen Shot 2021-04-02 a las 3.42.15 PM.png$

Figura 1. Tamiz de Eratóstenes hasta$n = 30$. Todos los múltiplos de un menos que$\sqrt{31}$ se cancelan. El resto son los primos menores que$n = 31$.

Una definición equivalente de primo es un número natural con precisamente dos divisores (distintos). El tamiz de Eratóstenes es un método simple y antiguo para generar una lista de primos para todos los números menores que, digamos, 225. Primero, enumere todos los enteros del 2 al 225. Comienza dando vueltas al número 2 y tachando todos sus múltiplos restantes: 4, 6, 8, etcétera. En cada paso, circule el número más pequeño sin marcar y tachar todos sus múltiplos restantes en la lista. Resulta que necesitamos tamizar solo múltiplos de$\sqrt{225} = 15$ y menos (ver ejercicio 2.4). Este método se ilustra si la Figura 1. Al terminar, los números primos son aquellos números que están rodeados o sin marcar en la lista.

Definición 1.4

Dejar$a$ y$b$ entrar$\mathbb{Z}$. Entonces$a$ y$b$ son relativamente primos si$\gcd(a, b) = 1$.

Definición 1.5

Dejar$a$ y$b$ entrar$\mathbb{Z}$ y$m \in \mathbb{N}$. Entonces$a$ es congruente al$b$ módulo m si$a+my = b$ para algunos$y \in \mathbb{Z}$ o$m | (b-a)$. Escribimos

\[\begin{array}{ccccc} {a = _{m}b}&{\mbox{or}}&{a = b \mod m}&{\mbox{or}}&{a \in b+m \mathbb{Z}} \end{array} \nonumber\]

Definición 1.6

El residuo de$a$ módulo$m$ es el entero (único)$r$ en$\{0, \cdots, m-1\}$ tal que$a = _{m}r$. Se denota por$\mbox{Res} _{m}(a)$.

Estas nociones son piedras angulares de gran parte de la teoría de números como veremos. Pero también son muy comunes en todo tipo de aplicaciones. Para in- postura, nuestras expresiones para el tiempo en el reloj no son más que contar módulo 12 o 24. Determinar cuántas horas transcurren entre las 4pm y las 3am de la mañana siguiente es un ejercicio sencillo para trabajar con aritmética modular, es decir: cálculos que involucran congruencias.