2.6: Ejercicios

Ejercicio\(\PageIndex{1}\)

Aplicar el algoritmo de división a los siguientes pares numéricos. (Pista: reemplace los números negativos por los positivos.)

1. \(110, 7\).
2. \(51, -30\).
3. \(-138, 24\).
4. \(272, 119\).
5. \(2378, 1769\).
6. \(270, 175560\).

Ejercicio\(\PageIndex{2}\)

En este ejercicio expondremos el algoritmo de división aplicado a polinomios\(x+1\) y\(3x^3+2x+1\) con coeficientes en\(\mathbb{Q}, \mathbb{R}\), o\(\mathbb{C}\).

1. Aplicar división larga para dividir\(3021\) por\(11\). (Pista:\(3021 = 11 \cdot 275 -4\).)
2. Aplica exactamente el mismo algoritmo para dividir\(3x^3+2x+1\) por\(x+1\). En este algoritmo,\(x^k\) se comporta como\(10^k\) en (a). (Pista: cada paso, cancela el poder más alto de\(x\).)
3. Verifica que obtengas\(3x^3+2x+1 = (x+1)(3x^2-3x+5)-4\).
4. Demostrar que en general, si\(p_{1}\) y\(p_{2}\) son polinomios tales que el grado de\(p_{1}\) es mayor o igual al grado de\(p_{2}\), entonces\(p_{1} = q_{2}p_{2}+p_{3}\), donde el grado de\(p_{3}\) es menor que el grado de\(p_{2}\). (Pista: realizar división larga como en (b). Deténgase cuando el grado del resto sea menor que el de\(p_{2}\).)
5. ¿Por qué esta división no funciona para polinomios con coeficientes adentro\(\mathbb{Z}\)? (Pista: reemplazar\(x+1\) por\(2x+1\).)

1. Ejercicio\(\PageIndex{3}\)
2. Calcula por división larga eso\(3021 = 11 \cdot 274+7\).
3. Concluir del ejercicio 2.2 que\(3021 = 11(300-30+5)-4\). (Pista: let\(x = 10\).)
4. Concluir del ejercicio 2.2 que\(3 \cdot 163 +2 \cdot 16+1 = 17(3 \cdot 162-3 \cdot 16+5)-4\). (Pista: let\(x = 16\).)

Ejercicio\(\PageIndex{4}\)

1. Utilice factorización única para mostrar que cualquier número compuesto\(n\) debe tener un factor primo menor o igual a\(\sqrt{n}\).
2. Usa ese hecho para probar: Si aplicamos el tamiz de Eratosthenes a\(\{2, 3, \cdots, n\}\), es suficiente tamizar números menores o iguales a\(\sqrt{n}\).

Ejercicio\(\PageIndex{5}\)

Damos una prueba elemental de Corolario 2.15.

1. Demostrar que\(a \cdot \frac{b}{\gcd (a,b)}\) es un múltiplo de\(a\).
2. Demostrar que\(\frac{b}{\gcd (a,b)} \cdot b\) es un múltiplo de\(b\).
3. Concluir que\(\frac{ab}{\gcd (a,b)}\) es un múltiplo de ambos\(a\) y\(b\) y por lo tanto mayor o igual a\(\mbox{lcm} (a,b)\).
4. Mostrar que\(a/(\frac{ab}{\mbox{lcm} (a,b)}) = \frac{\mbox{lcm} (a,b)}{b}\) es un entero. Así\(\frac{ab}{\mbox{lcm} (a,b)}\) es un divisor de\(a\).
5. De igual manera, mostrar que\(\frac{ab}{\mbox{lcm} (a,b)}\) es un divisor de\(b\).
6. Concluir eso\(\frac{ab}{\mbox{lcm} (a,b)} \le \gcd (a,b)\).
7. Termina la prueba.

Ejercicio\(\PageIndex{6}\)

Es posible extender la definición de\(\gcd\) y\(\mbox{lcm}\) a más de dos enteros (no todos los cuales son cero). Por ejemplo\(\gcd (24, 27, 54) = 3\).

1. Cómputos\(\gcd (6,10,15)\) y\(\mbox{lcm} (6,10,15)\).
2. Dé un ejemplo de un triple cuyo\(\gcd\) es uno, pero cada par de los cuales tiene un\(\gcd\) mayor que uno.
3. Demostrar que no hay triple\(\{a,b,c\}\) cuyos\(\mbox{lcm}\) iguales\(abc\), sino cada par de los cuales tiene lcm menos que el producto de ese par. (Pista: considerar\(\mbox{lcm} (a \cdot b) \cdot c\).)

Ejercicio\(\PageIndex{7}\)

1. Dar la factorización prima de los siguientes números:\(12, 392, 1043, 31, 128, 2160, 487\).
2. Dar la factorización prima de los siguientes números:\(12 \cdot 392, 1043 \cdot 31, 128 \cdot 2160\).
3. Dar la factorización prima de:\(1, 250000, 63^3, 720\), y el producto de los últimos tres números.

Ejercicio\(\PageIndex{8}\)

Utilice el Teorema Fundamental de la Aritmética para demostrar:

1. El lema de Be ́zout.
2. Lema de Euclides.

Ejercicio\(\PageIndex{9}\)

Para enteros positivos\(m\) y\(n\), supongamos que\(m^{\alpha} = n\). Demuestre que\(\alpha = \frac{p}{q}\) con\(\gcd(p,q) = 1\) si y solo si

\[\begin{array}{ccccc} {m = \prod_{i=1}^{s} p_{i}^{k_{i}}}&{and}&{n = \prod_{i=1}^{s} p_{i}^{l_{i}}}&{with}&{\forall i pk_{i} = ql_{i}} \end{array} \nonumber\]

Ejercicio\(\PageIndex{10}\)

Desarrollamos la prueba del Teorema 2.16 tal como fue dada por Euler. Comenzamos asumiendo que hay una lista finita\(L\) de\(k\) primos. Mostraremos en los siguientes pasos cómo esa suposición lleva a una contradicción. Ordenamos la lista según orden ascendente de magnitud de los primos. Entonces\(p_{1} = 2, p_{2} = 3, p_{3} = 5\),\(L = \{p_{1}, p_{2}, \cdots, p_{k}\}\) dónde, y así sucesivamente, hasta el último primo\(p_{k}\).

1. Demostrar que\(\prod_{i=1}^{k} \frac{p_{i}}{p_{i}-1}\) es finito, digamos\(M\).
2. Demostrar que para\(r > 0\),\[\prod_{i=1}^{k} \frac{p_{i}}{p_{i}-1} = \prod_{i=1}^{k} \frac{1}{1-p_{i}^{-1}} > \prod_{i=1}^{k} \frac{1-p_{i}^{-r-1}}{1-p_{i}^{-1}} = \prod_{i=1}^{k} (\sum_{ j=0}^{r} p_{i}^{-j}) \nonumber\]
3. Utilizar el teorema fundamental de la aritmética para mostrar que existe un\(\alpha (r) > 0\) tal que\[\prod_{i=1}^{k} (\sum_{ j=0}^{r} p_{i}^{-j}) = \sum_{l=1}^{\alpha (r)} \frac{1}{l}+R \nonumber\], donde\(R\) es un resto no negativo.
4. Demuestre que para todos\(K\) hay\(r\) tal que\(\alpha (r) > K\).
5. Así para cualquiera\(K\), hay\(r\) tal que\[\prod_{i=1}^{k} (\sum_{ j=0}^{r} p_{i}^{-j}) \ge \sum_{l=1}^{K} \frac{1}{l} \nonumber\]
6. Concluir con una contradicción entre a) y e). (Pista: la serie armónica\(\sum \frac{1}{l}\) diverge o ver ejercicio 2.11 c).)

Ejercicio\(\PageIndex{11}\)

En este ejercicio consideramos la función zeta de Riemann para valores reales de\(s\) mayor que\(1\).

1. Demuéstralo para todos\(x > -1\), tenemos\(\mbox{ln} (1+x) \le x\).
2. Utilice la Proposición 2.20 y a) para demostrar que\[\mbox{ln} \zeta (s) \le \sum_{\mbox{p prime}} \frac{p^{-s}}{1-p^{-s}} \le \sum_{\mbox{p prime}} \frac{p^{-s}}{1-2^{-s}} \nonumber\]
3. Utilice el siguiente argumento para demostrarlo\(\lim_{s \rightarrow 1} \zeta (s) = \infty\). \[\sum_{n=1}^{\infty} n^{-1} \ge \sum_{n=1}^{\infty} n^{-s} \ge \int_{1}^{\infty} x^{-s} dx \nonumber\](Para la última desigualdad, véase la Figura 4.)
4. Demostrar que b) y c) implican que\(\sum_{\mbox{p prime}} p^{-s}\) diverge como\(s \rightarrow 1\).
5. Demostrar que —en cierto sentido— los primos son más frecuentes que los cuadrados en los números naturales. (Pista:\(\sum_{n=1}^{\infty} n^{-2}\) converge.)

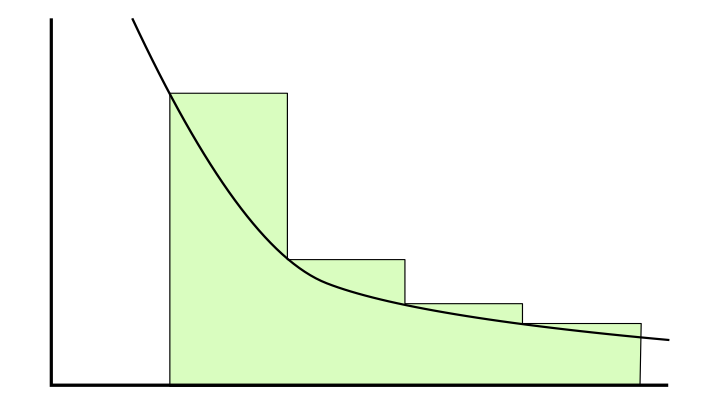
Figura 4. Prueba que\(\sum_{n=1}^{\infty} f(n)\) es mayor que\(\int_{1}^{\infty} x^{-s} dx\) si\(f\) es positiva y decreciente.

Ejercicio\(\PageIndex{12}\)

\(E\)Déjese ser el conjunto de números pares. Dejar\(a, c\) entrar\(E\), entonces\(c\) es divisible por\(a\) si hay\(ab \in E\) así que\(ab = c\). Definir un primo\(p\) en\(E\) como un número en\(E\) tal que no hay\(a\) y\(b\) en\(E\) con\(ab = p\).

1. Enumere los primeros\(30\) primos en\(E\).
2. ¿Se mantiene el lema de Euclides\(E\)? Explique.
3. Factor 60 en primos (in\(E\)) de dos maneras diferentes.

Ejercicio\(\PageIndex{13}\)

Ver ejercicio 2.12. Demostrar que cualquier número en\(E\) es producto de primos en\(E\). (Pista: seguir la prueba del Teorema 2.14, parte (1).)

Ejercicio\(\PageIndex{14}\)

Ver ejercicio 2.12 que muestra que la factorización única no se sostiene\(E = \{2, 4, 6, \dots\}\). La prueba de factorización única utiliza el lema de Euclides. A su vez, el lema de Euclides era un corolario del lema de Be ́zout, que depende del algoritmo de división. ¿Dónde exactamente se descompone la cadena en este caso?

Ejercicio\(\PageIndex{15}\)

\(L = \{p_{1}, p_{2}, \cdots\}\)Sea la lista de todos los primos, ordenados según magnitud ascendente. \(p_{n+1} \le \prod_{i=1}^{n} p_{i}\)Demuéstralo. (Pista: considerar\(d\) como en la prueba del Teorema 2.16, dejar\(p_{n+1}\) ser el divisor primo más pequeño de\(d-1\).)

Una versión mucho más fuerte del ejercicio 2.15 es el llamado Postulado de Bertrand. Ese teorema dice que para cada\(n \ge 1\), hay un prime in\(\{n+1, \dots, 2n\}\). Fue probado por Chebyshev. Posteriormente la prueba fue simplificada por Ramanujan y Erdo ̈s [18].

Ejercicio\(\PageIndex{16}\)

Dejar\(p\) y\(q\) cema mayor o igual a\(5\).

1. Demuestre que\(p = 12q+r\) dónde\(r \in \{1,5,7,11\}\). (Lo mismo vale para\(q\).)
2. \(24|p^2-q^2\)Demuéstralo. (Pista: use (a) para reducir esto a\({4 \choose 2} = 6\) casos.)

Ejercicio\(\PageIndex{17}\)

Un número completo cuadrado es un número\(n > 1\) tal que cada factor primo ocurre con una potencia al menos\(2\). Un número libre cuadrado es un número\(n > 1\) tal que cada factor primo ocurre con una potencia como máximo\(1\).

1. Si\(n\) es cuadrado lleno, demuestre que hay enteros positivos\(a) and \(b\) tales que\(n = a^{2}b^{3}\).
2. Mostrar que cada entero mayor que uno es el producto de un número libre cuadrado y un número cuadrado.

Ejercicio\(\PageIndex{18}\)

\(L = \{p_{1}, p_{2},\dots\}\)Sea la lista de todos los primos, ordenados ac- cording magnitud ascendente. Los números\(E_{n} = 1 + \prod_{i=1}^{n} p_{i}\) se llaman números Euclides.

1. Comprobar la primalidad de\(E_{1}\) a través\(E_{6}\).
2. Mostrar que\(E_{n} = _{4} 3\_. (Hint: \(E_{n}-1\) es dos veces un número impar.)
3. Mostrar eso para\(n \le 3\) la representación decimal de los\(E_{n}\) extremos en a\(1\). (Pista: mira los factores de\(E_{n}\).)

Ejercicio\(\PageIndex{19}\)

Los primos gemelos son un par de primos de la forma\(p\) y\(p+2\).

1. Demostrar que el producto de dos primos gemelos más uno es un cuadrado.
2. Demostrar que\(p > 3\), la suma de primos gemelos es divisible por\(12\). (Pista: ver ejercicio 2.16)

Ejercicio\(\PageIndex{20}\)

Demostrar que hay arbitrariamente grandes brechas entre primos sucesivos. Más precisamente, mostrar que cada entero en\(\{n!+2, n!+3, \dots n!+n\}\) es compuesto.

La declaración habitual para el teorema fundamental de la aritmética incluye solo números naturales\(n \in \mathbb{N}\) (es decir, no\(\mathbb{Z}\)) y la prueba común utiliza inducción en n. Revisamos esa prueba en los dos siguientes problemas.

Ejercicio\(\PageIndex{21}\)

1. \(2\)Demostrar que se puede escribir como producto de primos.
2. Vamos\(k > 2\). Supongamos que todos los números en\(\{1, 2, \dots k\}\) pueden escribirse como un producto de primos (o\(1\)). Mostrar que\(k+1\) es primo o compuesto.
3. Si en (b),\(k+1\) es primo, entonces todos los números en\(\{1, 2, \dots k+1\}\) pueden escribirse como un producto de primos (o\(1\)).
4. Si en (b),\(k+1\) es compuesto, entonces hay un divisor\(d \in \{2,\dots k\}\) tal que\(k+1 = dd'\).
5. Mostrar que la hipótesis en (b) implica también en este caso, todos los números en\(\{1, 2, \dots k+1\}\) pueden escribirse como un producto de primos (o\(1\)).
6. Utilice lo anterior para formular la prueba inductiva de que todos los elementos de\(\mathbb{N}\) pueden escribirse como producto de primos.

Ejercicio\(\PageIndex{22}\)

La configuración de la prueba es la misma que en el ejercicio 2.21. Usar inducción en\(n\). Asumimos el resultado de ese ejercicio.

1. Espectáculo que\(n = 2\) tiene una factorización única.
2. Supongamos que si for\(k > 2, \{2, \dots k\}\) puede ser factorizado de manera única. Luego hay primos\(p_{i}\) y\(q_{i}\), no necesariamente distintos, tales que\[k+1 = \prod_{i=1}^{s} p_{i} = \prod_{i=1}^{r} q_{i} \nonumber\]
3. Demostrar que luego\(p_{1}\) divide\(\prod_{i=1}^{r} q_{i}\) y así, Corolario 2.12 implica que hay\(j \le r\) tal que\(p_{1} = q_{j}\).
4. Relabel el\(q_{i}'\) s, para que\(p_{1} = q_{1}\) y divídalo\(n\) por\(p_{1} = q_{1}\). Demostrar que\[\frac{k+1}{q_{1}} = \prod_{i=2}^{s} p_{i} = \prod_{i=2}^{r} q_{i} \nonumber\]
5. Mostrar que la hipótesis en (b) implica que el restante\(p_{i}\) es igual al restante\(q_{i}\). (Pista:\(\frac{k}{q_{1}} \le k\).)
6. Utilice lo anterior para formular la prueba inductiva de que todos los elementos de\(\mathbb{N}\) pueden ser factorizados de manera única como un producto de primos.

Aquí hay una caracterización diferente de gcd y lcm. Lo demostramos como corolario del teorema de factorización prima.

Corolario 2.23

1. Un divisor común\(d > 0\) de\(a\) e\(b\) igual\(\gcd(a, b)\) si y solo si cada divisor común de\(a\) y\(b\) es un divisor de\(d\).
2. Además, un múltiplo común\(d > 0\) de\(a\) e\(b\) igual\(\mbox{lcm} (a, b)\) si y solo si cada múltiplo común de\(a\) y\(b\) es un múltiplo de\(d\).

Ejercicio\(\PageIndex{23}\)

Utilizar la caracterización de\(\gcd(a, b)\) y\(\mbox{lcm} (a,b)\) dada en la prueba del Corolario 2.15 para acreditar el Corolario 2.23.

Ejercicio\(\PageIndex{24}\)

1. Dejar\(p\) ser un prime fijo. Mostrar que la probabilidad de que dos enteros elegidos independientemente en\(\{1,2,\cdots,n\}\) sean divisibles por\(p\) tiende a\(\frac{1}{p^2}\) como\(n \rightarrow \infty\). Equivalentemente, la probabilidad de que no sean divisibles por\(p\) tiende a\(1-\frac{1}{p^2}\).
2. Hacer las suposiciones necesarias, y mostrar que la probabilidad de que dos enteros elegidos independientemente en no\(\{1,2,\cdots,n\}\) sean divisibles por ningún primo tiende a\(\prod_{p prime} (1-p^{-2})\). (Pista: hay que asumir que las probabilidades en 1. son independientes y así se pueden multiplicar.)
3. Mostrar que a partir de la fórmula del producto 2. y de Euler, se deduce que para 2 enteros aleatorios (positivos)\(a\) y\(b\) tener\(\gcd (a,b) = 1\) tiene probabilidad\(1/\zeta (2) \approx 0.61\)
4. Mostrar que\(d >1\) los enteros\(\{a_{1}, a_{2}, \cdots, a_{d}\}\) que la probabilidad es igual\(1/\zeta(d)\). (Pista: el razonamiento es el mismo que en 1., 2., 3.)
5. \(d \ge 2\)Demuéstralo\[1 < \zeta (d) < 1+\int_{1}^{\infty} x^{-d} dx \nonumber\] para: Para la última desigualdad, ver Figura 5.
6. Demostrar que para grandes\(d\), la probabilidad que\(\gcd (a_{1},a_{2},\cdots,a_{d}) = 1\) tiende a\(1\).

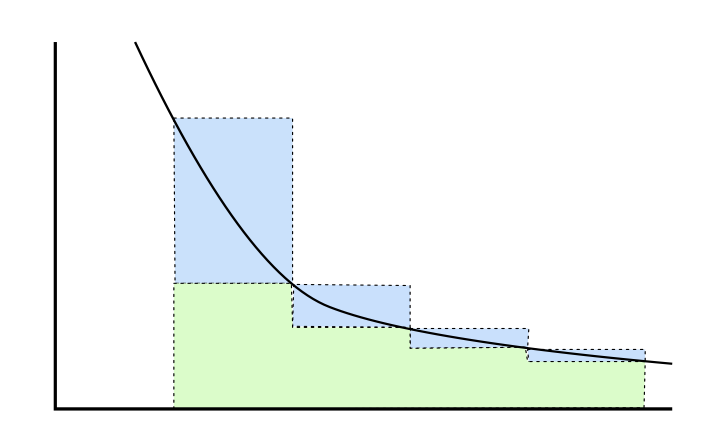
Figura 5. Prueba de que\(\sum_{n=1}^{\infty} f(n)\) (sombreado) menos\(f(1)\) (sombreado en azul) es menor que\(\int_{1}^{\infty} x^{-s} dx\) es positivo y decreciente.

Ejercicio\(\PageIndex{25}\)

Este ejercicio en base al ejercicio 2.24.

1. En la\(\{-4,\cdots, 4\}^2 \backslash (0,0)\) cuadrícula en\(\mathbb{Z}^{2}\), averigua qué propuesta de los puntos de celosía es visible desde el origen, ver Figura 6.
2. Demostrar que en una cuadrícula grande, esta propuesta tiende a\(1/\zeta (2)\).
3. Mostrar que a medida que la dimensión aumenta hasta el infinito, la proposición de los puntos de celosía\(\mathbb{Z}^{d}\) que son visibles desde el origen, aumenta a 1.

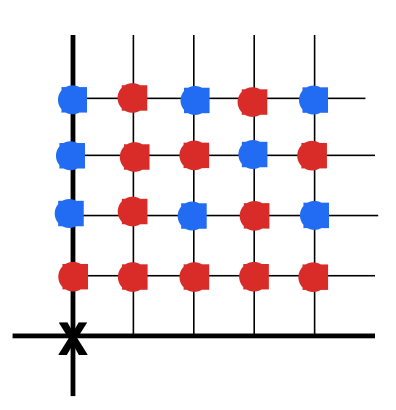
Figura 6. El origen está marcado por “\(\times\)”. Los puntos rojos son visibles desde\(\times\); entre cualquier punto azul y\(\times\) hay un punto rojo. La imagen muestra exactamente una cuarta parte de\(\{-4,\cdots ,4\}^{2} \backslash (0,0) \subset \mathbb{Z}^2\).