2.5: La hipótesis de Riemann
- Page ID
- 111526
Definición 2.19
La función zeta de Riemann\(\zeta(z)\) es una función compleja definida de la siguiente manera en\(\{z \in \mathbb{C} | \mbox{Re}z > 1\}\)
\[\zeta (z) = \sum_{n=1}^{\infty} n^{-z} \nonumber\]
En otros valores de la\(z \in \mathbb{C}\) misma se define por la continuación analítica de esta función (excepto en\(z = 1\) donde tiene un polo simple).
La continuación analítica es semejante a reemplazar\(e^x\) donde\(x\) es real por\(e^z\) donde\(z\) es complejo. Otro ejemplo es la serie\(\sum_{j=0}^{\infty} z^j\). Esta serie diverge para\(|z| > 1\). Pero como función analítica, puede ser reemplazada por\((1-z)^{-1}\) en todos\(\mathbb{C}\) excepto en el polo\(z = 1\) donde diverge.
Recordemos que una función analítica es una función diferenciable. Equivalentemente, es una función que viene dada localmente por una serie de potencias convergentes. Si\(f\) y\(g\) son dos continuaciones analíticas a una región\(U\) de una función\(h\) dada en una región\(V \subset U\), entonces la diferencia\(f-g\) es cero en algunas\(U\) y por lo tanto todas sus expansiones de potencia son cero y por lo tanto debe ser cero en toda la región. De ahí que las conjugaciones analíticas sean únicas. Esa es la razón por la que tienen sentido. Para más detalles, véase por ejemplo [4, 14].
Es costumbre denotar el argumento de la función zeta por\(s\). Lo haremos de aquí en adelante. Tenga en cuenta que\(|n-s| = n-\mbox{Re} s\), y así para\(\mbox{Re} s > 1\) la serie es absolutamente convergente. En este punto, el alumno debe recordar —o mirar hacia arriba en [23 ]— el hecho de que las series absolutamente convergentes se pueden reorganizar arbitrariamente sin cambiar la suma. Esto lleva a la siguiente proposición.
Proposición 2.20
Para\(\mbox{Re} s > 1\) nosotros tenemos
\[\sum_{n=1}^{\infty} n-s = \prod_{p prime} (1-p^{-s})^{-1} \nonumber\]
Hay dos pruebas comunes de esta fórmula. Vale la pena presentar ambos.
- Prueba
-
La primera prueba utiliza el Teorema Fundamental de la Aritmética. En primer lugar, recordamos que utilizan series geométricas
\[(1-p^{-s})^{-1} = \sum_{k=0}^{\infty} p^{-ks} \nonumber\]
para reescribir la mano derecha del producto Euler. Esto da
\[\prod_{p prime} (1-p^{-s})^{-1} = (\sum_{k_1 = 0}^{\infty} p_{1}^{-k_{1}s}) (\sum_{k_2 = 0}^{\infty} p_{2}^{-k_{2}s}) (\sum_{k_3 = 0}^{\infty} p_{3}^{-k_{3}s}) \nonumber\]
Reorganización de términos rendimientos
\[\dots = (p_{1}^{k_{1}}p_{2}^{k_{2}}p_{3}^{k_{3}} \dots)^{-s} \nonumber\]
Por el Teorema Fundamental de la Aritmética, la expresión\((p_{1}^{k_{1}}p_{2}^{k_{2}}p_{3}^{k_{3}} \dots)\) recorre todos los enteros positivos exactamente una vez. Así, al volver a ordenar obtenemos la mano izquierda de la fórmula de Euler.
La segunda prueba, la que utilizó Euler, emplea un método de tamiz. Esta vez, comenzamos con la mano izquierda del producto Euler. Si multiplicamos\(\zeta\) por\(2^{-s}\), recuperamos precisamente los términos con\(n\) par. Entonces
\[(1-2^{-s}) \zeta(s) = 1+3^{-s}+5^{-s}+\cdots = \sum_{2 \nmid n} n^{-s} \nonumber\]
Posteriormente multiplicamos esta expresión por\((1-3^{-s})\). Esto tiene el efecto de eliminar los términos que quedan donde\(n\) es un múltiplo de\(3\). De ello se deduce que eventualmente
\[(1-p_{l}^{-s}) \dots (1-p_{1}^{-s}) \zeta (s) = \sum_{p_{1} \nmid n, \cdots p_{l} \nmid n} n^{-s} \nonumber\]
El argumento utilizado en el tamiz de Eratóstenes (Sección 1.1) sirve ahora para mostrar que en el lado derecho de la última ecuación todos los términos que no sean\(1\) desaparecen ya que l tiende al infinito. Por lo tanto, la mano izquierda tiende a 1, lo que implica la proposición.
El teorema más importante respecto a los primos es probablemente el siguiente (sin pruebas).
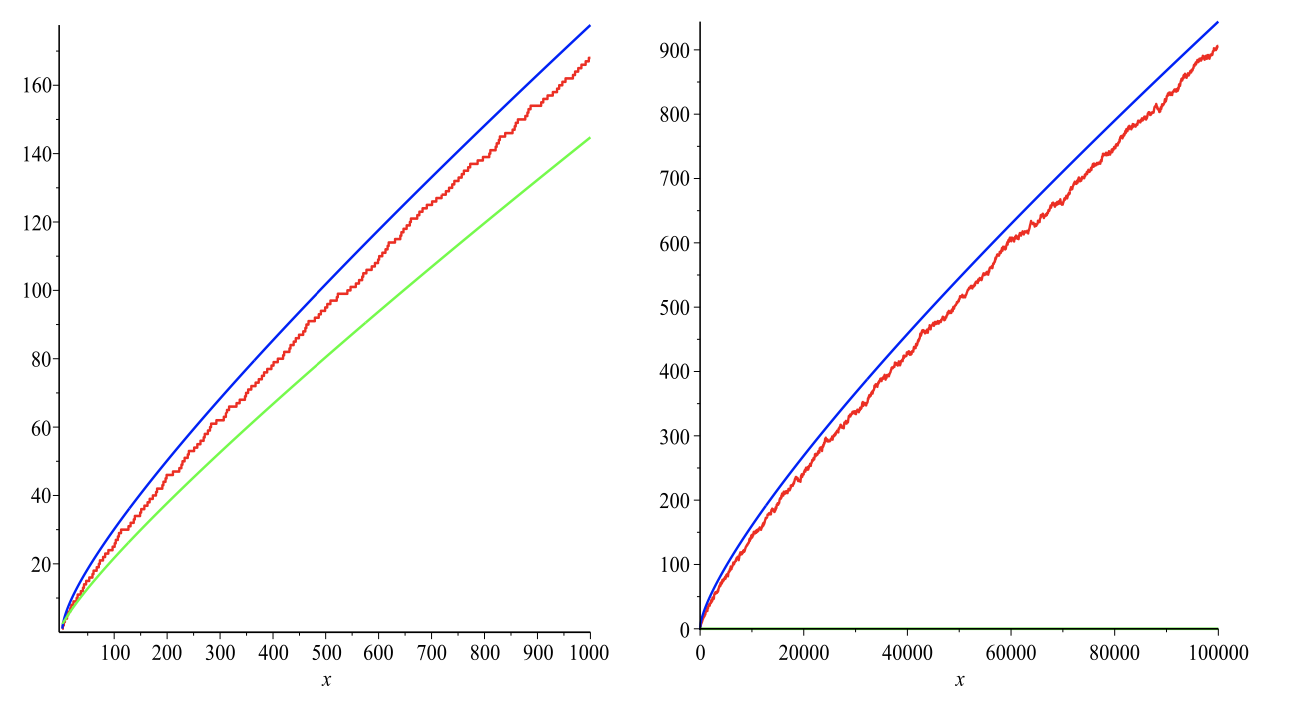
Figura 3. A la izquierda, la función\(\int_{2}^{x} \mbox{ln} t dt\) en azul,\(\pi (x)\) en rojo y\(x/ \mbox{ln}x\) en verde. A la derecha, tenemos\(\int_{2}^{x} \mbox{ln} t dt - x/\mbox{ln} x\) en azul,\(\pi (x)- x/\mbox{ln} x\) en rojo.
Teorema 2.21 (Teorema de números primos)
Let\(\pi (x)\) denotar la función de conteo primo, es decir: el número de primos menor o igual a\(x > 2\).
Entonces
- \(\lim_{x \rightarrow \infty} \frac{\pi (x)}{(x/\mbox{ln} x)} = 1\)y
- \(\lim_{x \rightarrow \infty} \frac{\pi (x)}{\int_{2}^{x} \mbox{ln} t dt} = 1\)
donde\(\mbox{ln}\) está el logaritmo natural.
La primera estimación es la más fácil de probar, la segunda es la más precisa. En la Figura 3 de la izquierda, trazamos, para\(x \in [2,1000]\), de arriba a abajo las funciones\(\int_{2}^{x} \mbox{ln} t dt\) en azul,\(\pi (x)\) en rojo, y\(x/\mbox{ln} x\). En la figura derecha, aumentamos el dominio a\(x \in [2, 100000]\). y trazamos la diferencia de estas funciones con\(x/\mbox{ln} x\). Ahora queda claro que de hecho\(\int_{2}^{x} \mbox{ln} t dt\) es una aproximación mucho mejor de\(\pi (x)\). A partir de esta cifra se puede tentar a concluir que siempre\(\int_{2}^{x} \mbox{ln} t dt - \pi (x)\) es mayor o igual a cero. Esto, sin embargo, es falso. Se sabe que hay infinitamente muchos n para los cuales\(\int_{2}^{x} \mbox{ln} t dt - \pi (x) < 0\). El primero de ellos\(n\) se llama el número de Skewes. No se sabe mucho de este número, salvo que es menor a 10317.
Quizás el problema abierto más importante en todas las matemáticas es el siguiente. Se refiere a la continuación analítica de\(\zeta (s)\) lo anterior.
Conjetura 2.22 (Hipótesis de Riemann)
Todos los ceros no reales de\(\zeta (s)\) mentira en la línea\(\mbox{Re} s = \frac{1}{2}\)
En su único trabajo sobre teoría de números [20], Riemann se dio cuenta de que la hipótesis le permitió describir propiedades detalladas de la distribución de primos en términos de la ubicación del cero no real de\(\zeta (s)\). Esta conexión completamente inesperada entre campos tan dispares —funciones analíticas y primos en—,\(\mathbb{N}-\) habló a la imaginación y provocó un enorme interés por el tema. En investigaciones posteriores, se ha demostrado que la hipótesis también está relacionada con otras áreas de las matemáticas, como, por ejemplo, los espaciamientos entre valores propios de matrices hermitianas aleatorias [2], e incluso la física [5, 6].


