12: Conceptos y Herramientas
- Page ID
- 117221
Presentamos aquí los conceptos y herramientas que son útiles en el estudio de sistemas dinámicos no lineales.
Análisis de puntos fijos y estabilidad lineal
Considere la ecuación diferencial unidimensional para\(x=x(t)\) dada por
\[\dot{x}=f(x) \nonumber \]
Decimos que\(x_{*}\) es un punto fijo, o punto de equilibrio, de\((12.1)\) si\(f\left(x_{*}\right)=0\), de manera que en un punto fijo,\(\dot{x}=0 .\) El nombre punto fijo es apto ya que la solución a\((12.1)\) con condición inicial\(x(0)=x_{*}\) es fija en\(x(t)=x_{*}\) todo momento\(t\).
Un punto fijo, sin embargo, puede ser estable o inestable. Se dice que un punto fijo es estable si una pequeña perturbación decae en el tiempo; se dice que es inestable si una pequeña perturbación crece en el tiempo.
Podemos determinar la estabilidad mediante un análisis lineal. Let\(x=x_{*}+\epsilon(t)\), donde\(\epsilon\) representa una pequeña perturbación de la solución desde el punto fijo\(x_{*} .\) Porque\(x_{*}\) es una constante,\(\dot{x}=\dot{\epsilon} ;\) y porque\(x_{*}\) es un punto fijo,\(f\left(x_{*}\right)=0\). Serie Taylor expandiéndose sobre\(\epsilon=0\), tenemos
\[\begin{aligned} \dot{\epsilon} &=f\left(x_{*}+\epsilon\right) \\ &=f\left(x_{*}\right)+\epsilon f^{\prime}\left(x_{*}\right)+\ldots \\ &=\epsilon f^{\prime}\left(x_{*}\right)+\ldots \end{aligned} \nonumber \]
Los términos omitidos en la expansión de la serie Taylor son proporcionales a\(\epsilon^{2}\), y pueden hacerse insignificantes, al menos en un intervalo de tiempo corto, tomando\(\epsilon(0)\) pequeños. La ecuación diferencial a considerar,\(\dot{\epsilon}=f^{\prime}\left(x_{*}\right) \epsilon\), es por lo tanto lineal, y tiene la solución
\[\epsilon(t)=\epsilon(0) e^{f^{\prime}\left(x_{*}\right) t} \nonumber \]
La perturbación de la solución de punto\(x(t)=x_{*}\) fijo decae o crece exponencialmente dependiendo del signo de\(f^{\prime}\left(x_{*}\right)\). Por lo tanto, la condición de estabilidad\(x_{*}\) es
\[x_{*} \text { is } \begin{cases}\text { a stable fixed point if } & f^{\prime}\left(x_{*}\right)<0, \\ \text { an unstable fixed point if } & f^{\prime}\left(x_{*}\right)>0 .\end{cases} \nonumber \]
Para el caso especial\(f^{\prime}\left(x_{*}\right)=0\), decimos que el punto fijo es marginalmente estable. Veremos que las bifurcaciones suelen ocurrir en valores de parámetros donde los puntos fijos se vuelven marginalmente estables.
Las ecuaciones de diferencia, o mapas, pueden analizarse de manera similar. Considere el mapa unidimensional dado por
\[x_{n+1}=f\left(x_{n}\right) \text {. } \nonumber \]
Decimos que\(x_{n}=x_{*}\) es un punto fijo del mapa si\(x_{*}=f\left(x_{*}\right) .\) La estabilidad de este punto fijo se puede determinar\(x_{n}=x_{*}+\epsilon_{n}\) entonces escribiendo para que\((12.4)\) se convierta
\[\begin{aligned} x_{*}+\epsilon_{n+1} &=f\left(x_{*}+\epsilon_{n}\right) \\ &=f\left(x_{*}\right)+\epsilon_{n} f^{\prime}\left(x_{*}\right)+\ldots \\ &=x_{*}+\epsilon_{n} f^{\prime}\left(x_{*}\right)+\ldots . \end{aligned} \nonumber \]
Por lo tanto, al orden de liderazgo en\(\epsilon\),
\[\left|\frac{\epsilon_{n+1}}{\epsilon_{n}}\right|=\left|f^{\prime}\left(x_{*}\right)\right| \text {, } \nonumber \]
y la condición de estabilidad\(x_{*}\) para un mapa unidimensional es
\[x_{*} \quad \text { is } \quad \begin{cases}\text { a stable fixed point if } & \left|f^{\prime}\left(x_{*}\right)\right|<1 \\ \text { an unstable fixed point if } & \left|f^{\prime}\left(x_{*}\right)\right|>1\end{cases} \nonumber \]
Aquí, la estabilidad marginal ocurre cuando\(\left|f^{\prime}\left(x_{*}\right)\right|=1\), y las bifurcaciones generalmente ocurren en valores de parámetros donde el punto fijo se vuelve marginalmente estable. Si\(f^{\prime}\left(x_{*}\right)=0\), entonces el punto fijo se llama superestable. Perturbaciones a un punto fijo superestable decaimiento especialmente rápido, haciendo cálculos numéricos en puntos fijos superestables más rápidamente convergentes.
Las herramientas de análisis de estabilidad lineal y punto fijo también son aplicables a sistemas de ecuaciones de orden superior. Considerar el sistema bidimensional de ecuaciones diferenciales dado por
\[\dot{x}=f(x, y), \quad \dot{y}=g(x, y) . \nonumber \]
Se dice que el punto\(\left(x_{*}, y_{*}\right)\) es un punto fijo de\((12.7)\) si\(f\left(x_{*}, y_{*}\right)=0\) y\(g\left(x_{*}, y_{*}\right)=0 .\) Nuevamente, la estabilidad local de un punto fijo se puede determinar mediante un análisis lineal. Dejamos\(x(t)=x_{*}+\epsilon(t)\) y\(y(t)=y_{*}+\delta(t)\), donde\(\epsilon\) y\(\delta\) son pequeñas perturbaciones independientes desde el punto fijo. Haciendo uso de la serie Taylor bidimensional de\(f(x, y)\) y\(g(x, y)\) sobre el punto fijo, o equivalentemente sobre\((\epsilon, \delta)=(0,0)\), tenemos
\[\begin{aligned} \dot{\epsilon} &=f\left(x_{*}+\epsilon, y_{*}+\delta\right) \\ &=f_{*}+\epsilon \frac{\partial f_{*}}{\partial x}+\delta \frac{\partial f_{*}}{\partial y}+\ldots \\ &=\epsilon \frac{\partial f_{*}}{\partial x}+\delta \frac{\partial f_{*}}{\partial y}+\ldots, \\ \dot{\delta} &=g\left(x_{*}+\epsilon, y_{*}+\delta\right) \\ &=g_{*}+\epsilon \frac{\partial g_{*}}{\partial x}+\delta \frac{\partial g_{*}}{\partial y}+\ldots \\ &=\epsilon \frac{\partial g_{*}}{\partial x}+\delta \frac{\partial g_{*}}{\partial y}+\ldots, \end{aligned} \nonumber \]
donde en la serie Taylor\(f_{*}, g_{*}\) y las derivadas parciales marcadas de manera similar todas denotan funciones evaluadas en el punto fijo. Despreciando términos de orden superior en la serie Taylor, tenemos así un sistema de odas para la perturbación, dado en forma de matriz como
\[\frac{d}{d t}\left(\begin{array}{c} \epsilon \\ \delta \end{array}\right)=\left(\begin{array}{cc} \partial f_{*} / \partial x & \partial f_{*} / \partial y \\ \partial g_{*} / \partial x & \partial g_{*} / \partial y \end{array}\right)\left(\begin{array}{c} \epsilon \\ \delta \end{array}\right) \nonumber \]
La matriz de dos por dos en (12.8) se llama la matriz jacobiana en el punto fijo. Un análisis de valores propios de la matriz jacobiana normalmente dará dos valores propios\(\lambda_{1}\) y\(\lambda_{2}\). Estos valores propios pueden ser reales y distintos, pares conjugados complejos o repetidos. El punto fijo es estable (todas las perturbaciones decaen exponencialmente) si ambos valores propios tienen partes reales negativas. El punto fijo es inestable (algunas perturbaciones crecen exponencialmente) si al menos un valor propio tiene una parte real positiva. Los puntos fijos se pueden clasificar además como nodos estables o inestables, puntos de sillín inestables, puntos espirales estables o inestables, o nodos inadecuados estables o inestables.
Bifurcaciones
Para los sistemas no lineales, pequeños cambios en los parámetros del sistema pueden resultar en cambios cualitativos en la dinámica. Estos cambios cualitativos se llaman bifurcaciones. Aquí consideramos cuatro bifurcaciones clásicas de ecuaciones diferenciales no lineales unidimensionales: la bifurcación de nodo de silla de montar, la bifurcación transcrítica y las bifurcaciones de horca supercrítica y subcrítica. La ecuación diferencial que consideraremos está escrita en general como
\[\dot{x}=f_{r}(x), \nonumber \]
donde el subíndice\(r\) representa un parámetro que da como resultado una bifurcación cuando se varía a través de cero. Las ecuaciones diferenciales más simples que exhiben estas bifurcaciones se denominan las formas normales, y corresponden a un análisis local (es decir, expansión de la serie Taylor) de ecuaciones diferenciales más generales alrededor del punto fijo, junto con una posible reescalación de\(x\).
Bifurcación de nodo de silla
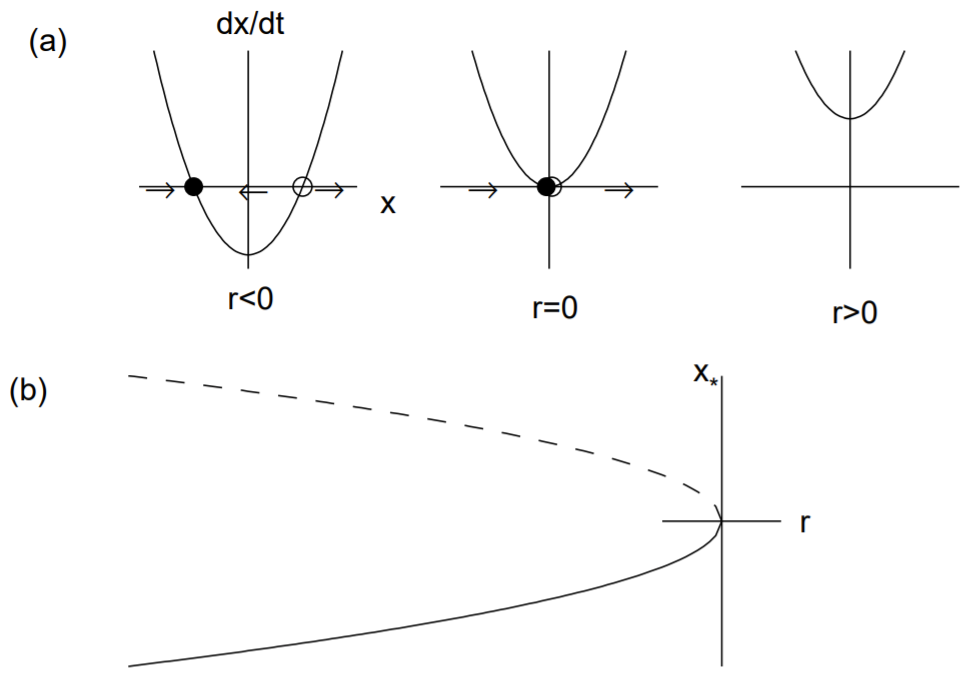
La bifurcación del nodo de silla da como resultado la creación o destrucción de puntos fijos. La forma normal para una bifurcación de nodo de silla de montar viene dada por
\[\dot{x}=r+x^{2} . \nonumber \]
Los puntos fijos son\(x_{*}=\pm \sqrt{-r}\). Claramente, existen dos puntos fijos reales cuando\(r<0\) y no existen puntos fijos reales cuando\(r>0\). La estabilidad de los puntos fijos cuando\(r<0\) están determinados por el
derivado de\(f(x)=r+x^{2}\), dado por\(f^{\prime}(x)=2 x .\) Por lo tanto, el punto fijo negativo es estable y el punto fijo positivo es inestable.
Podemos ilustrar esta bifurcación. Primero, en la Fig. 12.1 (a), trazamos\(\dot{x}\) versus\(x\) para los tres valores de parámetros correspondientes a\(r<0, r=0\) y\(r>0\). Los valores en los que\(\dot{x}=0\) corresponden a los puntos fijos, y se dibujan flechas que indican cómo\(x(t)\) evoluciona la solución (a la derecha si\(\dot{x}>0\) y a la izquierda si\(\dot{x}<0\)). El punto fijo estable se indica mediante un círculo relleno y el punto fijo inestable por un círculo abierto. Tenga en cuenta que cuando\(r=0\), las soluciones convergen al origen desde la izquierda, pero divergen del origen de la derecha.
Segundo, trazamos el diagrama de bifurcación estándar en la Fig. 12.1 (b), donde\(x_{*}\) se grafica el punto fijo versus el parámetro de bifurcación\(r\). Como es costumbre, el punto fijo estable se denota con una línea continua y el punto fijo inestable por una línea discontinua. Tenga en cuenta que los dos puntos fijos chocan y aniquilan en\(r=0\), y no hay puntos fijos para\(r>0\).
Bifurcación transcrítica
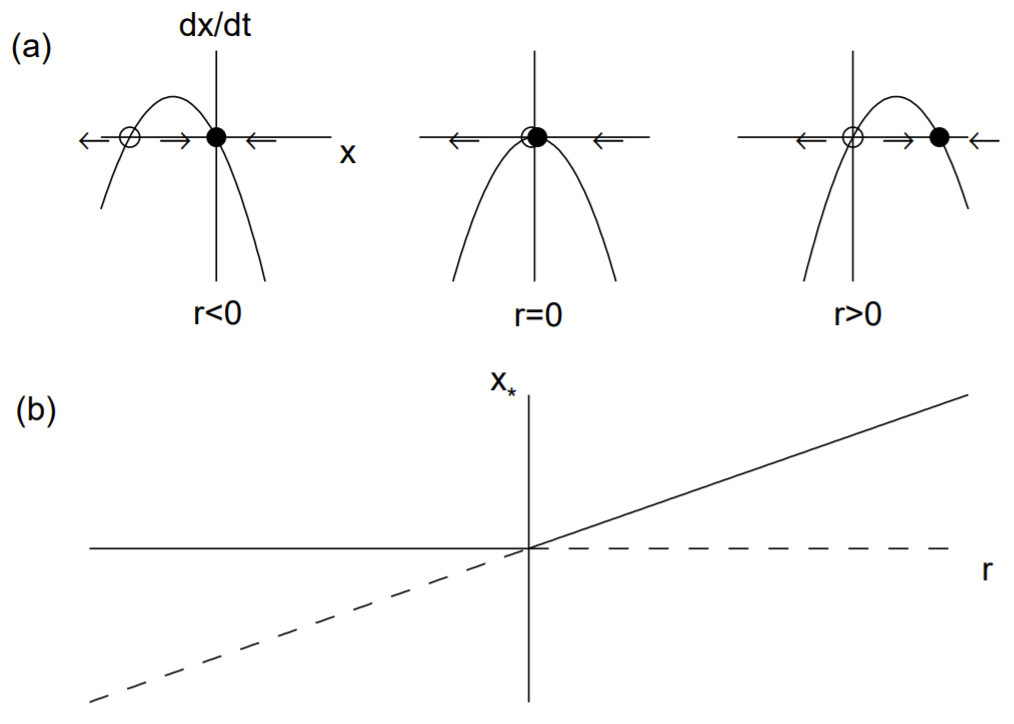
Una bifurcación transcrítica ocurre cuando hay un intercambio de estabilidades entre dos puntos fijos. La forma normal para una bifurcación transcrítica viene dada por
\[\dot{x}=r x-x^{2} . \nonumber \]
Los puntos fijos son\(x_{*}=0\) y\(x_{*}=r\). El derivado del lado derecho es\(f^{\prime}(x)=r-2 x\), para que\(f^{\prime}(0)=r\) y\(f^{\prime}(r)=-r\). Por lo tanto, for\(r<0, x_{*}=0\) es estable y\(x_{*}=r\) es inestable, mientras que for\(r>0, x_{*}=r\) es estable y\(x_{*}=0\) es inestable. Los dos puntos fijos intercambian así la estabilidad a medida que\(r\) pasa por cero. La bifurcación transcrítica se ilustra en la Fig. 12.2.
Bifurcaciones de horca
Las bifurcaciones de horca ocurren cuando un punto fijo se convierte en tres en el punto de bifurcación. Las bifurcaciones de horca suelen asociarse con los fenómenos físicos llamados ruptura de simetría. Las bifurcaciones de horca vienen en dos tipos. En la bifurcación de horca supercrítica, la estabilidad del punto fijo original cambia de estable a inestable y se crea un nuevo par de puntos fijos estables por encima (súper) del punto de bifurcación. En la bifurcación subcrítica, la estabilidad del punto fijo original cambia nuevamente de estable a inestable pero se crea un nuevo par de puntos fijos ahora inestables debajo (sub-) del punto de bifurcación.
Bifurcación supercrítica
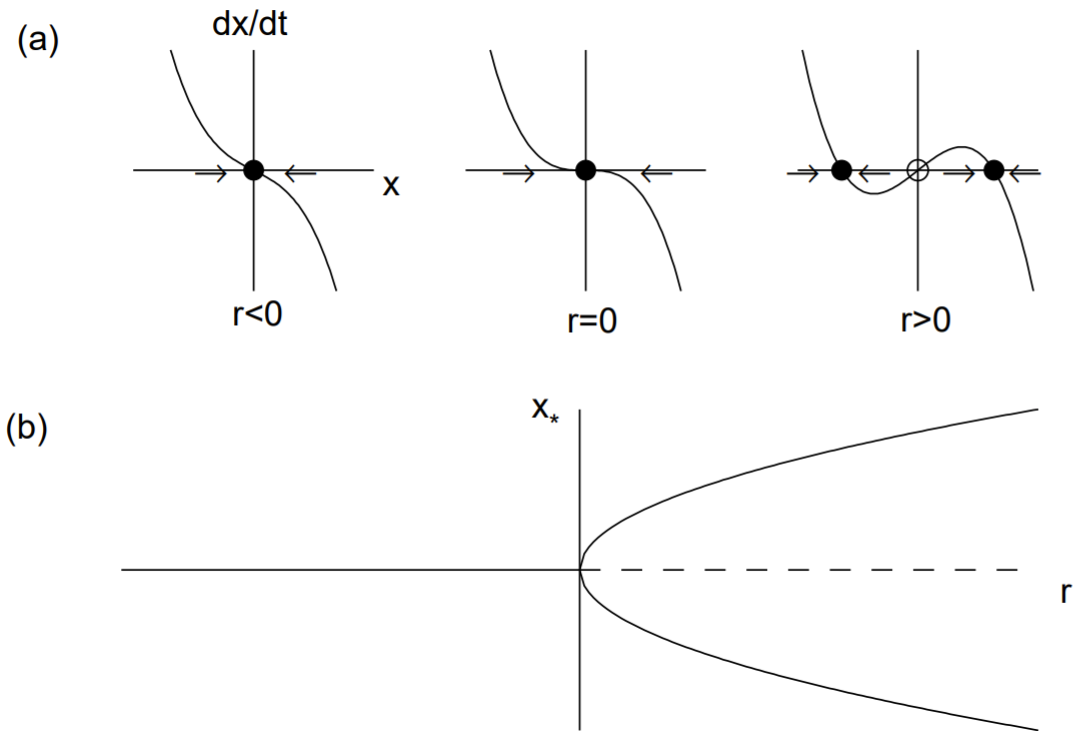
La forma normal para la bifurcación supercrítica de horca viene dada por
\[\dot{x}=r x-x^{3} \nonumber \]
Tenga en cuenta que el término lineal da como resultado un crecimiento exponencial cuando\(r>0\) y el término no lineal estabiliza este crecimiento. Los puntos fijos son\(x_{*}=0\) y\(x_{*}=\pm \sqrt{r}\), estos últimos puntos fijos existentes sólo cuando\(r>0\). El derivado de\(f\) es\(f^{\prime}(x)=r-3 x^{2}\) para que\(f^{\prime}(0)=r\) y\(f^{\prime}(\pm \sqrt{r})=-2 r\). Por lo tanto, el punto fijo\(x_{*}=0\) es estable\(r<0\) e inestable\(r>0\) mientras los puntos fijos\(x=\pm \sqrt{r}\) existen y son estables para\(r>0 .\) Observe que el punto fijo\(x_{*}=0\) se vuelve inestable como \(r\)cruza cero y nacen dos nuevos puntos\(x_{*}=\pm \sqrt{r}\) fijos estables. La bifurcación supercrítica de horca se ilustra en la Fig. 12.3.
La bifurcación de la horca ilustra la física de la ruptura de simetría. La ecuación diferencial (12.12) es invariante bajo la transformación\(x \rightarrow-x\). Las soluciones de punto fijo de esta ecuación que obedecen a esta misma simetría se denominan simétricas; los puntos fijos que no se denominan asimétricos. Aquí,\(x_{*}=0\) es el punto fijo simétrico y\(x=\pm \sqrt{r}\) son asimétricos. Los puntos fijos asimétricos siempre ocurren en pares, y reflejan las características de estabilidad entre sí. Sólo las condiciones iniciales determinan qué punto fijo asimétrico se alcanza asintóticamente.
Bifurcación de horca subcrítica
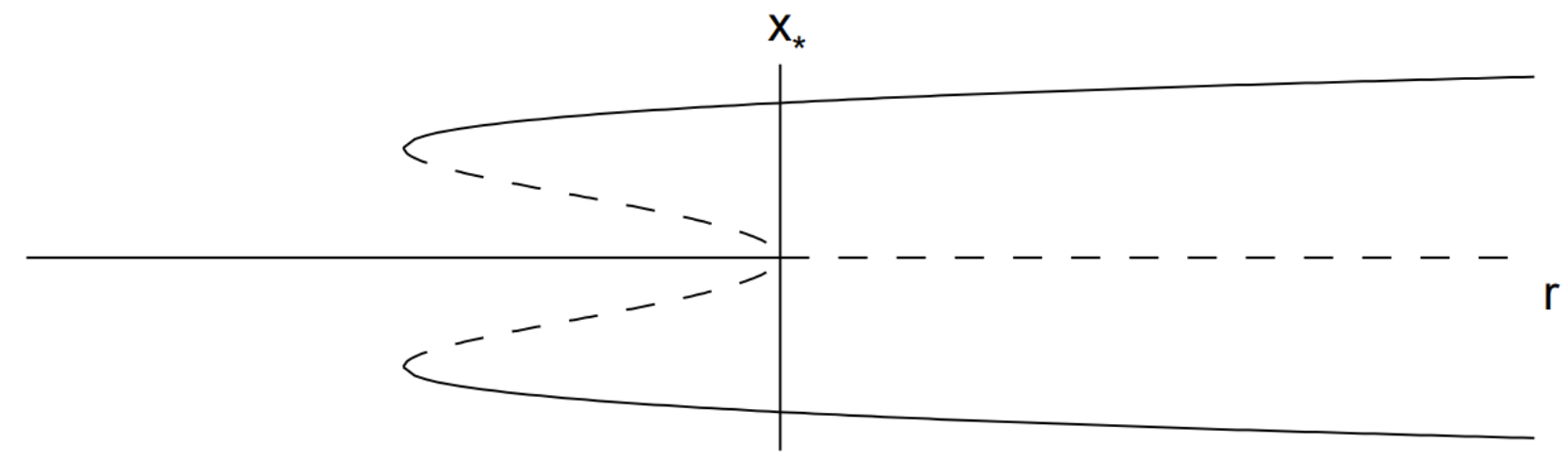
En el caso subcrítico, el término cúbico es desestabilizador. La forma normal (ordenar\(x^{3}\)) es
\[\dot{x}=r x+x^{3} \nonumber \]
Los puntos fijos son\(x_{*}=0\) y\(x_{*}=\pm \sqrt{-r}\), estos últimos puntos fijos existentes sólo cuando\(r \leq 0\). La derivada del lado derecho es\(f^{\prime}(x)=r+3 x^{2}\) así que\(f^{\prime}(0)=r\) y\(f^{\prime}(\pm \sqrt{-r})=-2 r .\) Por lo tanto, el punto fijo\(x_{*}=0\) es estable para\(r<0\) e inestable para\(r>0\) mientras que los puntos fijos\(x=\pm \sqrt{-r}\) existen y son inestables para\(r<0\). No hay puntos fijos estables cuando\(r>0\).
La ausencia de puntos fijos estables para\(r>0\) indica que el descuido de términos de orden\(x\) superior en que\(x^{3}\) en la forma normal puede ser injustificado. Manteniendo la simetría intrínseca de las ecuaciones (solo potencias impares de\(x\) para que la ecuación sea invariante cuando\(x \rightarrow-x\)) podemos agregar un término estabilizador no lineal proporcional a\(x^{5}\). La forma normal extendida (a la orden\(x^{5}\)) es
\[\dot{x}=r x+x^{3}-x^{5}, \nonumber \]
y es algo más difícil de analizar. Los puntos fijos son soluciones de
\[x\left(r+x^{2}-x^{4}\right)=0 . \nonumber \]
El punto fijo\(x_{*}=0\) existe para todos\(r\), y se pueden encontrar cuatro puntos fijos adicionales a partir de las soluciones de la ecuación cuadrática en\(x^{2}\):
\[x_{*}=\pm \sqrt{\frac{1}{2}(1 \pm \sqrt{1+4 r})} . \nonumber \]
Estos puntos fijos existen sólo si\(x_{*}\) es real. Claramente, para que la raíz cuadrada interior sea real,\(r \geq-1 / 4\). También observa que\(1-\sqrt{1+4 r}\) se vuelve negativo para\(r>0\). Por lo tanto, tenemos tres intervalos\(r\) a considerar, y estas regiones y sus puntos fijos son
\[\begin{aligned} r<-\frac{1}{4}: & x_{*}=0 \quad \text { (one fixed point); } \\ -\frac{1}{4}<r<0: & x_{*}=0, \quad x_{*}=\pm \sqrt{\frac{1}{2}(1 \pm \sqrt{1+4 r})} \quad \text { (five fixed points); } \\ r>0: \quad x_{*}=0, \quad x_{*}=\pm \sqrt{\frac{1}{2}(1+\sqrt{1+4 r})} \quad \text { (three fixed points). } \end{aligned} \nonumber \]
La estabilidad se determina a partir de\(f^{\prime}(x)=r+3 x^{2}-5 x^{4} .\) Ahora,\(f^{\prime}(0)=r\) por lo que\(x_{*}=0\) es estable para\(r<0\) e inestable para\(r>0\). El cálculo para las otras cuatro raíces puede simplificarse señalando que\(x_{*}\) satisface\(r+x_{*}^{2}-x_{*}^{4}=0\), o\(x_{*}^{4}=r+x_{*}^{2} .\) Por lo tanto,
\[\begin{aligned} f^{\prime}\left(x_{*}\right) &=r+3 x_{*}^{2}-5 x_{*}^{4} \\ &=r+3 x_{*}^{2}-5\left(r+x_{*}^{2}\right) \\ &=-4 r-2 x_{*}^{2} \\ &=-2\left(2 r+x_{*}^{2}\right) \end{aligned} \nonumber \]
Con\(x_{*}^{2}=\frac{1}{2}(1 \pm \sqrt{1+4 r})\), tenemos
\[\begin{aligned} f^{\prime}\left(x_{*}\right) &=-2\left(2 r+\frac{1}{2}(1 \pm \sqrt{1+4 r})\right) \\ &=-((1+4 r) \pm \sqrt{1+4 r}) \\ &=-\sqrt{1+4 r}(\sqrt{1+4 r} \pm 1) \end{aligned} \nonumber \]
Claramente, la raíz más siempre es estable ya que\(f^{\prime}\left(x_{*}\right)<0 .\) La raíz menos existe solo para\(-\frac{1}{4}<r<0\) y es inestable ya que\(f^{\prime}\left(x_{*}\right)>0 .\) Resumimos la estabilidad de los diversos puntos fijos:
\[\begin{aligned} r<-\frac{1}{4}: \quad x_{*} &=0 \quad(\text { stable }) ; \\ -\frac{1}{4}<r<0: \quad x_{*} &=0, \quad(\text { stable }) \\ x_{*} &=\pm \sqrt{\frac{1}{2}(1+\sqrt{1+4 r})} \quad \text { (stable); } \\ x>0: \quad x_{*} &=\pm \sqrt{\frac{1}{2}(1-\sqrt{1+4 r})} \quad \text { (unstable); } \\ x_{*} &=0 \quad(\text { unstable }) \\ x_{*} &=\pm \sqrt{\frac{1}{2}(1+\sqrt{1+4 r})} \quad \text { (stable). } \end{aligned} \nonumber \]
El diagrama de bifurcación se muestra en la Fig. 12.4. Observe que hay además de una bifurcación de horca subcrítica en el origen, hay dos bifurcaciones simétricas de silla de montar que ocurren cuando\(r=-1 / 4\).
Podemos imaginar lo que sucede con la solución a la oda a medida que\(r\) aumenta a partir de valores negativos, suponiendo que haya algo de ruido en el sistema para que\(x(t)\) fluctúe alrededor de un punto fijo estable. Para\(r<-1 / 4\), la solución\(x(t)\) fluctúa alrededor del punto fijo estable\(x_{*}=0\). A medida que\(r\) aumenta en el rango\(-1 / 4<r<0\), la solución permanecerá cerca del punto fijo estable\(x_{*}=0 .\) Sin embargo, una llamada catástrofe ocurre tan pronto como se pierde\(r>0 .\) El punto\(x_{*}=0\) fijo y la solución se saltar hacia arriba (o hacia abajo) hasta el único punto fijo restante. Una catástrofe similar puede ocurrir como\(r\) disminuciones a partir de valores positivos. En este caso, el salto ocurre tan pronto como sea\(r<-1 / 4\). Dado que el comportamiento de\(x(t)\) es diferente dependiendo de si aumentamos o disminuimos\(r\), decimos que el sistema exhibe histéresis. La existencia de una bifurcación de horca subcrítica puede ser muy peligrosa en aplicaciones de ingeniería, ya que un pequeño cambio en los parámetros físicos de un problema puede resultar en un gran cambio en el estado de equilibrio. Físicamente, esto puede resultar en el colapso de una estructura.
bifurcaciones Hopf
Un nuevo tipo de bifurcación puede ocurrir en dos dimensiones. Supongamos que hay algún parámetro de control\(\mu\). Además, supongamos que para\(\mu<0\), un sistema bidimensional se aproxima a un punto fijo mediante oscilaciones amortiguadas exponencialmente. Sabemos que la matriz jacobiana en el punto fijo con\(\mu<0\) tendrá complejos valores propios conjugados con partes reales negativas. Ahora supongamos que cuando\(\mu>0\) las partes reales de los valores propios se vuelven positivas para que el punto fijo se vuelva inestable. Este cambio en la estabilidad del punto fijo se denomina bifurcación Hopf. Las bifurcaciones Hopf también vienen en dos tipos: una bifurcación Hopf supercrítica y una bifurcación Hopf subcrítica. Para la bifurcación supercrítica de Hopf, a medida que\(\mu\) aumenta ligeramente por encima de cero, la oscilación resultante alrededor del punto fijo ahora inestable se estabiliza rápidamente a pequeña amplitud, y se obtiene un ciclo límite. Para la bifurcación subcrítica de Hopf, a medida que\(\mu\) aumenta ligeramente por encima de cero, el ciclo límite salta inmediatamente a gran amplitud.
Retratos de fase
El espacio de fase de un sistema dinámico consiste en las variables dinámicas independientes. Por ejemplo, el espacio de fase de las ecuaciones de péndulo amortiguadas y conducidas dadas por (11.15) es tridimensional y consiste en\(\theta, u\) y\(\phi\). Las ecuaciones no forzadas tienen solo un espacio de fase bidimensional, que consiste en\(\theta\) y\(u\).
Una característica importante de los caminos en el espacio de fase es que nunca pueden cruzarse excepto en un punto fijo, que puede ser estable si todos los caminos entran en el punto, o inestables si algunos caminos salen. Esto es consecuencia de la singularidad de la solución a una ecuación diferencial. Cada punto del diagrama de fase-espacio representa una posible condición inicial para las ecuaciones, y debe tener una trayectoria única asociada con esa condición inicial.
El péndulo simple es un sistema conservador, que exhibe una ley de conservación de la energía, y esto implica una conservación del área espacial de fase (o volumen). Sin embargo, el péndulo amortiguado no es conservador y esto implica una contracción del área (o volumen) del espacio de fase.
De hecho, es posible derivar una condición general para determinar si el volumen del espacio de fase se conserva o se contrae. Consideramos aquí, por conveniencia, ecuaciones en un espacio de fase tridimensional dado por
\[\dot{x}=F(x, y, z), \quad \dot{y}=G(x, y, z), \quad \dot{z}=H(x, y, z) . \nonumber \]
Podemos considerar un pequeño volumen de espacio de fase\(\Gamma=\Gamma(t)\), dado por
\[\Gamma(t)=\Delta x \Delta y \Delta z, \nonumber \]
donde
\[\Delta x=x_{1}(t)-x_{0}(t), \quad \Delta y=y_{1}(t)-y_{0}(t), \quad \Delta z=z_{1}(t)-z_{0}(t) \nonumber \]
El volumen inicial de espacio de fase en el momento\(t\) representa una caja con una esquina en el punto\(\left(x_{0}(t), y_{0}(t), z_{0}(t)\right)\) y la esquina opuesta en\(\left(x_{1}(t), y_{1}(t), z_{1}(t)\right)\). Esta caja inicial de espacio de fase evoluciona a lo largo del tiempo. Para determinar cómo\(\Delta x\) evoluciona un borde que emana de\(\left(x_{0}, y_{0}, z_{0}\right)\) con longitud, escribimos usando una expansión de la serie Taylor de primer orden en\(\Delta t\)
\[\begin{aligned} &x_{0}(t+\Delta t)=x_{0}(t)+\Delta t F\left(x_{0}, y_{0}, z_{0}\right) \\ &x_{1}(t+\Delta t)=x_{1}(t)+\Delta t F\left(x_{1}, y_{0}, z_{0}\right) \end{aligned} \nonumber \]
Por lo tanto,
\[\Delta x(t+\Delta t)=\Delta x(t)+\Delta t\left(F\left(x_{1}, y_{0}, z_{0}\right)-F\left(x_{0}, y_{0}, z_{0}\right)\right) \nonumber \]
restando\(\Delta x(t)\) de ambos lados y dividiendo por\(\Delta t\), tenemos como\(\Delta t \rightarrow 0\),
\[\frac{d}{d t}(\Delta x)=\left(F\left(x_{1}, y_{0}, z_{0}\right)-F\left(x_{0}, y_{0}, z_{0}\right)\right) . \nonumber \]
Con\(\Delta x\) pequeño, por lo tanto obtenemos a primer orden en\(\Delta x\),
\[\frac{d}{d t}(\Delta x)=\Delta x \frac{\partial F}{\partial x}, \nonumber \]
donde se evalúa la derivada parcial en el punto\(\left(x_{0}(t), y_{0}(t), z_{0}(t)\right)\).
Del mismo modo, también tenemos
\[\frac{d}{d t}(\Delta y)=\Delta y \frac{\partial G}{\partial y}, \quad \frac{d}{d t}(\Delta z)=\Delta z \frac{\partial H}{\partial z} \nonumber \]
Desde
\[\frac{d \Gamma}{d t}=\frac{d(\Delta x)}{d t} \Delta y \Delta z+\Delta x \frac{d(\Delta y)}{d t} \Delta z+\Delta x \Delta y \frac{d(\Delta z)}{d t} \nonumber \]
tenemos
\[\frac{d \Gamma}{d t}=\left(\frac{\partial F}{\partial x}+\frac{\partial G}{\partial y}+\frac{\partial H}{\partial z}\right) \Gamma \nonumber \]
válido para la evolución de una caja infinitesimal.
Podemos concluir de (12.25) que el volumen fase-espacio se conserva si la divergencia en el lado derecho desaparece, o que el volumen fase-espacio se contrae exponencialmente si la divergencia es negativa.
Por ejemplo, podemos considerar las ecuaciones para el péndulo amortiguado e impulsado dadas por (11.15). La divergencia en este caso se deriva de
\[\frac{\partial}{\partial \theta}(u)+\frac{\partial}{\partial u}\left(-\frac{1}{q} u-\sin \theta+f \cos \psi\right)+\frac{\partial}{\partial \psi}(\omega)=-\frac{1}{q} \nonumber \]
y siempre\(q>0\) (es decir, el péndulo está amortiguado), contratos de volumen fase-espacio. Para el péndulo no amortiguado (donde\(q \rightarrow \infty\)), se conserva el volumen del espacio de fase.
Límite de ciclos
El estado asintótico de un sistema no lineal puede ser un ciclo límite en lugar de un punto fijo. Un ciclo límite estable es una solución periódica en la que convergen todas las soluciones cercanas. Los ciclos límite también pueden ser inestables. Determinar la existencia de un ciclo límite a partir de un sistema no lineal de ecuaciones a través de medios analíticos suele ser imposible, pero los ciclos límite se encuentran fácilmente numéricamente. Las ecuaciones de péndulo accionadas y amortiguadas no tienen puntos fijos, pero sí tienen ciclos límite.
Atractores y cuencas de atracción
Un atractor es una configuración estable en el espacio de fase. Por ejemplo, un atractor puede ser un punto fijo estable o un ciclo límite. El péndulo amortiguado, no accionado, converge a un punto fijo estable correspondiente al péndulo en reposo en la parte inferior. El péndulo amortiguado y accionado para ciertos valores de los parámetros converge a un ciclo límite. Veremos que el péndulo caótico también tiene un atractor de otro tipo, llamado atractor extraño.
El dominio de atracción de un punto fijo estable, o de un ciclo límite, se denomina cuenca de atracción del atractor. La cuenca de atracción consiste en todas las condiciones iniciales para las cuales las soluciones convergen asintóticamente al atractor. Para sistemas no lineales, las cuencas de atracción pueden tener geometrías complicadas.
Secciones Poincaré
La sección de Poincaré es un método para reducir en una o más dimensiones los diagramas de espacio de fase de sistemas dimensionales superiores. Más comúnmente, un espacio de fase tridimensional se puede reducir a dos dimensiones, para lo cual una gráfica puede ser más fácil de interpretar. Para sistemas con una fuerza impulsora periódica como el sistema de péndulo amortiguado y accionado dado por (11.15), el espacio de fase bidimensional se\((\theta, u)\) puede ver estroboscópicamente, tomando el período estroboscópico el período de forzamiento, es decir\(2 \pi / \omega\). Para el péndulo amortiguado, impulsado, la tercera variable dinámica\(\psi\) satisface\(\psi=\psi_{0}+\omega t\), y el trazado de las variables fase-espacio\((\theta, u)\) en los tiempos\(t_{0}, t_{0}+2 \pi / \omega\)\(t_{0}+4 \pi / \omega\), etc., equivale a trazar los valores de \((\theta, u)\)cada vez que la variable fase-espacio\(\psi\) se incrementa por\(2 \pi\).
Para sistemas sin forzamiento periódico, se puede colocar un plano en el espacio de fase tridimensional, y se puede trazar un punto en este plano cada vez que la órbita pasa a través de él. Por ejemplo, si las variables dinámicas son\(x, y\) y\(z\), un plano podría colocarse en\(z=0\) y los valores de\((x, y)\) trazados cada vez que z pasa por cero. Por lo general, se especifica también la dirección de paso, de manera que un punto se traza sólo cuando\(\dot{z}>0\), digamos.
Dimensiones fractales
El atractor del péndulo caótico se llama extraño porque ocupa una dimensión fraccionaria del espacio de fase. Para entender lo que se entiende por dimensiones fraccionarias, primero revisamos algunos fractales clásicos.
Fractales clásicos
Conjunto Cantor
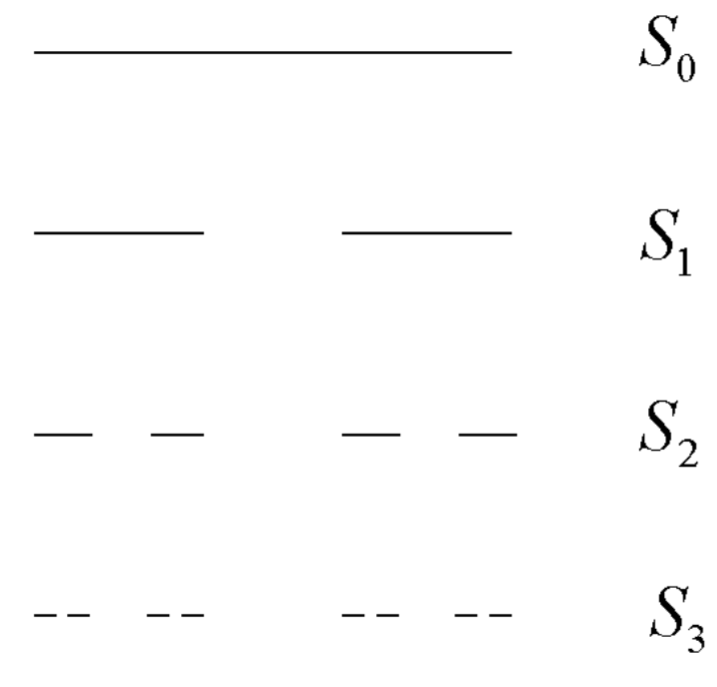
El conjunto Cantor tiene algunas propiedades inusuales. Primero, calculamos su longitud. Vamos a\(l_{n}\) denotar la longitud del conjunto\(S_{n} .\) Claramente,\(l_{0}=1 .\) ya que\(S_{1}\) se construye quitando el tercio medio de\(S_{0}\), tenemos\(l_{1}=2 / 3\). Para construir\(S_{2}\), nuevamente eliminamos el tercio medio de los dos segmentos de línea de\(S_{1}\), reduciendo la longitud de\(S_{1}\) por otro factor de\(2 / 3\), de modo que\(l_{2}=(2 / 3)^{2}\), y así sucesivamente. Obtenemos\(l_{n}=(2 / 3)^{n}\), y el\(\lim _{n \rightarrow \infty} l_{n}=0 .\) Por lo tanto, el conjunto Cantor tiene longitud cero.
El conjunto Cantor, entonces, no consiste en segmentos de línea. Sin embargo, el conjunto Cantor ciertamente no es un conjunto vacío. Podemos ver que en la etapa 1, hay dos puntos finales interiores\(1 / 3\) y\(2 / 3\), y estos nunca se eliminarán; en la etapa 2, están los extremos interiores adicionales\(1 / 9,2 / 9,7 / 9\) y\(8 / 9\); y en la etapa 3, agregamos ocho puntos finales interiores más. Vemos, entonces, que en etapa\(k\) sumamos\(2^{k}\) más puntos finales interiores. Por lo tanto, se incluye un número infinito pero contable de puntos finales en el conjunto Cantor.
Pero el conjunto Cantor consiste en mucho más que solo estos endpoints, y de hecho demostraremos que el conjunto Cantor es un conjunto incontable. Recordemos del análisis, que un conjunto infinito de puntos puede ser contable o incontable. Un conjunto contable de puntos es un conjunto que se puede poner en una correspondencia oneto-uno con el conjunto de números naturales. Como es bien sabido, el conjunto infinito de todos los números racionales es contable mientras que el conjunto infinito de números reales es incontable. Al enumerar los puntos finales del conjunto Cantor anterior, cada etapa agregando\(2^{k}\) más puntos finales, hemos demostrado que el conjunto de todos los puntos finales es un conjunto contable.
Para demostrar que el conjunto Cantor es incontable, es útil hacer uso de la representación base 3 de los números. Recordemos que cualquier número\(N\), dado por
\[N=\ldots \mathrm{a} * B^{3}+\mathrm{b} * B^{2}+\mathrm{c} * B+\mathrm{d} * B^{0}+\mathrm{e} * B^{-1}+\mathrm{f} * B^{-2}+\mathrm{g} * B^{-3}+\ldots, \nonumber \]
se puede escribir en base\(B\) como
\[N=\ldots \text { abcd.efg } \ldots \text { (base } B \text { ) } \nonumber \]
donde el período que separa la parte entera del número de la parte fraccionaria se denomina en general punto base. Para la base 10, por supuesto, el punto base se denomina punto decimal, y para la base 2, un punto binario.
Ahora, considera el conjunto de Cantor. En la primera etapa, todos los números que se encuentran entre\(1 / 3\) y se\(2 / 3\) eliminan. Los números restantes, entonces, deben ser de la forma\(0.0 \ldots\) (base 3) o\(0.2 \ldots\) (base 3), ya que (casi) todos los números que tienen la forma\(0.1 \ldots\) (base 3) se han eliminado. La única excepción es el punto final\(1 / 3=0.1\) (base 3), pero este número también se puede escribir como\(1 / 3=0.02\) (base 3), donde la barra sobre un número o números significa una repetición infinita. En la segunda etapa, todos los números que se encuentran entre\(1 / 9\) y\(2 / 9\), digamos, se eliminan, y estos números son de la forma\(0.01 \ldots\) (base 3). Podemos ver, entonces, que el conjunto Cantor puede definirse como el conjunto de todos los números en el intervalo unitario que no contienen 1's en su representación base 3.
Usando la notación base 3, es fácil encontrar un número que no sea un punto final, pero que esté en el conjunto Cantor. Por ejemplo, el número no\(1 / 4\) es un punto final. Podemos convertir\(1 / 4\) a base 3 por el siguiente cálculo:
\[\begin{aligned} \frac{1}{4} \times 3 &=0.75 \\ 0.75 \times 3 &=2.25 \\ 0.25 \times 3 &=0.75 \\ 0.75 \times 3 &=2.25 \end{aligned} \nonumber \]
y así sucesivamente, de donde encontramos eso\(1 / 4=0 . \overline{02}\) (base 3). El número\(1 / 4\), por lo tanto, no tiene 1's en su expansión base 3 y así es un elemento del conjunto Cantor.
Ahora podemos probar que el conjunto de Cantor es un conjunto incontable. La prueba es similar a la utilizada para demostrar que los números reales son incontables. Si suponemos que el conjunto Cantor es contable, entonces podemos enumerar todos sus elementos usando una expansión base 3; es decir,
\[\begin{aligned} &x_{1}=0 . x_{11} x_{12} x_{13} \ldots(\text { base } 3), \\ &x_{2}=0 . x_{21} x_{22} x_{23} \ldots(\text { base } 3), \\ &x_{3}=0 . x_{31} x_{32} x_{33} \ldots(\text { base } 3), \end{aligned} \nonumber \]
y así sucesivamente, donde todos los\(x_{i j}\)'s deben ser un 0 o un 2 (es decir, no se permiten 1). Ahora es sencillo nombrar un número que\(y\) no esté en esta lista. Tenemos
\[y=0 . y_{11} y_{22} y_{33} \cdots \nonumber \]
donde\(y_{11} \neq x_{11}, y_{22} \neq x_{22}, y_{33} \neq x_{33}\), etc.. Es decir, si\(x_{11}=0\), entonces\(y_{11}=2 ;\) si\(x_{11}=2\), entonces\(y_{11}=0\), y así sucesivamente. Al construir un número que no está en la lista, hemos obtenido una reductio ad absurdum, y podemos concluir que el conjunto Cantor es incontable.
Tenga en cuenta que los puntos finales del conjunto Cantor son solo aquellos números escritos en la base 3 que terminan con todos los 0 o todos los 2, y estos de hecho forman solo un subconjunto muy pequeño de todo el conjunto Cantor.
Desde la representación base 3, ahora podemos ver que el conjunto de Cantor tiene la siguiente característica interesante. Por un lado, cualquier pequeño intervalo alrededor de un punto en el conjunto Cantor contiene otro punto en el conjunto Cantor. Por otro lado, hay un intervalo entre dos puntos cualesquiera en el conjunto Cantor que no está en el conjunto Cantor. Por ejemplo, tomemos el punto\(1 / 4=0 . \overline{02}\) en el conjunto Cantor, y el intervalo\(\left[1 / 4-3^{-4}, 1 / 4+3^{-4}\right] .\) En base 3, el intervalo viene dado por\([0.0201 \overline{02}, 0.0210 \overline{02}]\). Hay, por supuesto, un número infinito de puntos en el Cantor establecidos en este intervalo, siendo uno de ellos\(0.0202\) a la izquierda de\(1 / 4\), y\(0.02022\) a la derecha de\(1 / 4\). Si el intervalo se estableció usando\(3^{-n}\), para cualquiera\(n\), todavía podemos encontrar otros puntos en el intervalo que están en el conjunto Cantor. También, entre dos puntos cualesquiera en el conjunto Cantor, hay un intervalo que se eliminó durante la construcción del conjunto Cantor. Entonces el conjunto Cantor no consta ni de segmentos de línea ni de un conjunto de puntos discretos.
El conjunto Cantor también es autosimilar, lo que significa que contiene copias más pequeñas de sí mismo en todas las escalas.
El conjunto Cantor se llama fractal, y se dice que tiene una dimensión fractal. Las dimensiones enteras nos son más familiares: decimos que una línea tiene dimensión 1; un área, dimensión 2; y un volumen, dimensión\(3 .\)
Para conjuntos autosimilares, podemos colocar la definición de dimensión sobre una base más matemática. Un segmento de línea, un cuadrado y un cubo también pueden considerarse autosimilares. Supongamos que un conjunto autosimilar\(S\) se compone de\(m\) copias de sí mismo escaladas por un factor de\(r\). Como ejemplos, el segmento de línea\([0,1]\) está compuesto por dos copias de sí mismo escaladas por un factor de dos; a saber, los segmentos\([0,1 / 2]\) y\([1 / 2,1]\). Un cuadrado está compuesto por cuatro copias de sí mismo escaladas por un factor de dos. Y un cubo está compuesto por ocho copias de sí mismo escaladas por un factor de dos. Escribimos
\[m=r^{D}, \nonumber \]
donde\(D\) se llama la dimensión de similitud del conjunto. Con\(r=2\), el segmento de línea tiene\(m=2\), el cuadrado tiene\(m=4\), y el cubo tiene\(m=8\), produciendo las dimensiones habituales\(D=1,2\) y 3, respectivamente.
Ahora el conjunto Cantor está compuesto por dos copias de sí mismo escaladas por un factor de tres. Por lo tanto,
\[2=3^{D}, \nonumber \]
y la dimensión de similitud del conjunto Cantor viene dada por\(D=\log 2 / \log 3 \approx 0.6309\), que tiene una dimensión menor que la de una línea, pero mayor que la de un punto.
Triángulo Sierpinski
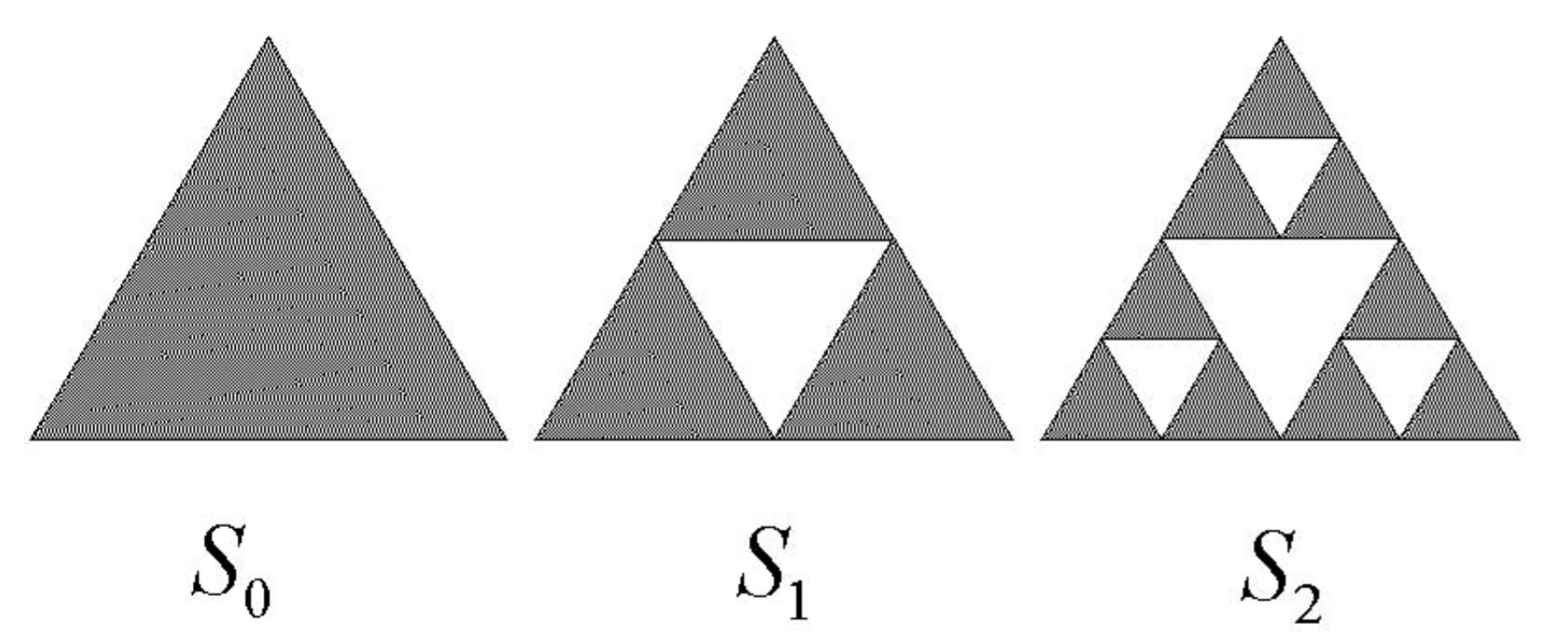
Otros fractales clásicos se pueden construir de manera similar al conjunto Cantor. El triángulo Sierpinski comienza con un triángulo equilátero,\(S_{0}\), con lados unitarios. Luego dibujamos líneas que conectan los tres puntos medios de los tres lados. Luego se elimina el triángulo medio equilátero recién formado de longitud\(1 / 2\) lateral\(S_{0}\) para formar el conjunto\(S_{1}\). Este proceso se repite sobre los triángulos equiláteros restantes, como se ilustra en la Fig. 12.6. El triángulo Sierpinski\(S\) se define como el límite de esta repetición; es decir,\(S=\lim _{n \rightarrow \infty} S_{n}\).
El triángulo Sierpinski está compuesto por tres copias de sí mismo escaladas por un factor de dos, de modo que
\[3=2^{D}, \nonumber \]
y la dimensión de similitud es\(D=\log 3 / \log 2 \approx 1.5850\), que tiene dimensión entre una línea y un área.
Similar al conjunto Cantor, el triángulo Sierpinksi, aunque existe en un espacio bidimensional, tiene área cero. Si dejamos\(A_{i}\) ser el área del conjunto\(S_{i}\), entonces como área se reduce por un factor de\(3 / 4\) con cada iteración, tenemos
\[A_{n}=\left(\frac{3}{4}\right)^{n} A_{0} \nonumber \]
así que eso\(A=\lim _{n \rightarrow \infty} A_{n}=0\).
Alfombra Sierpinski
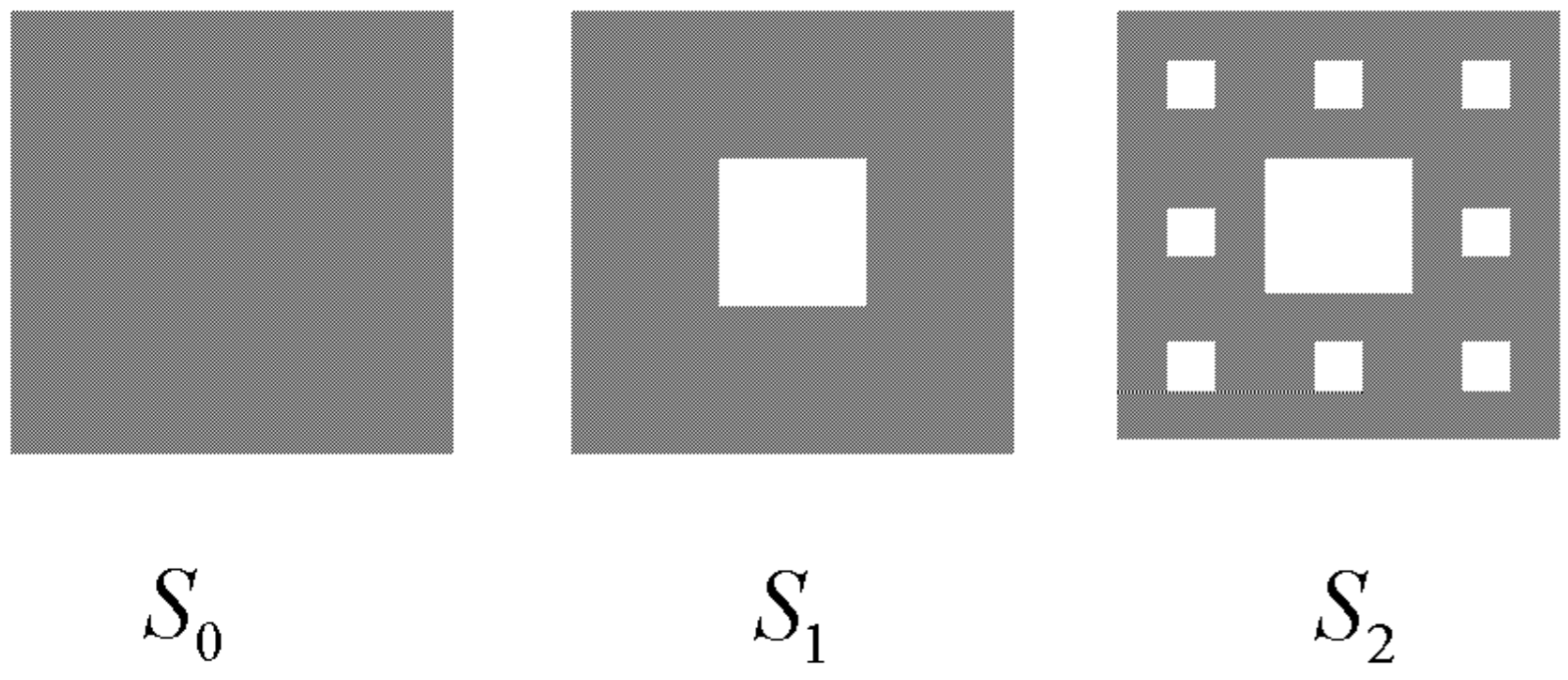
La alfombra Sierpinski comienza con un cuadrado,\(S_{0, \text { with unit sides. Here, we remove a center }}\) cuadrado de longitud lateral\(1 / 3\); el conjunto restante se llama\(S_{1}\). Este proceso se repite entonces como se ilustra en la Fig. 12.7.
Aquí, la alfombra Sierpinski está compuesta por ocho copias de sí misma escaladas por un factor de tres, de manera que
\[8=3^{D} \text {, } \nonumber \]
y la dimensión de similitud es\(D=\log 8 / \log 3 \approx 1.8928\), algo mayor que el triángulo Sierpinski. Se puede decir, entonces, que la alfombra Sierpinski llena más espacio que el triángulo Sierpinski, aunque todavía tiene área cero.
Curva de Koch
Al igual que el conjunto Cantor, comenzamos con el intervalo unitario, pero ahora reemplazamos el tercio medio por dos segmentos de línea de longitud\(1 / 3\), como se ilustra en\(12.8\), para formar el conjunto\(S_{1}\). Este proceso se repite entonces en los cuatro segmentos de línea de longitud\(1 / 3\) para formar\(S_{2}\), y así sucesivamente, como se ilustra en la Fig. \(12.8\).
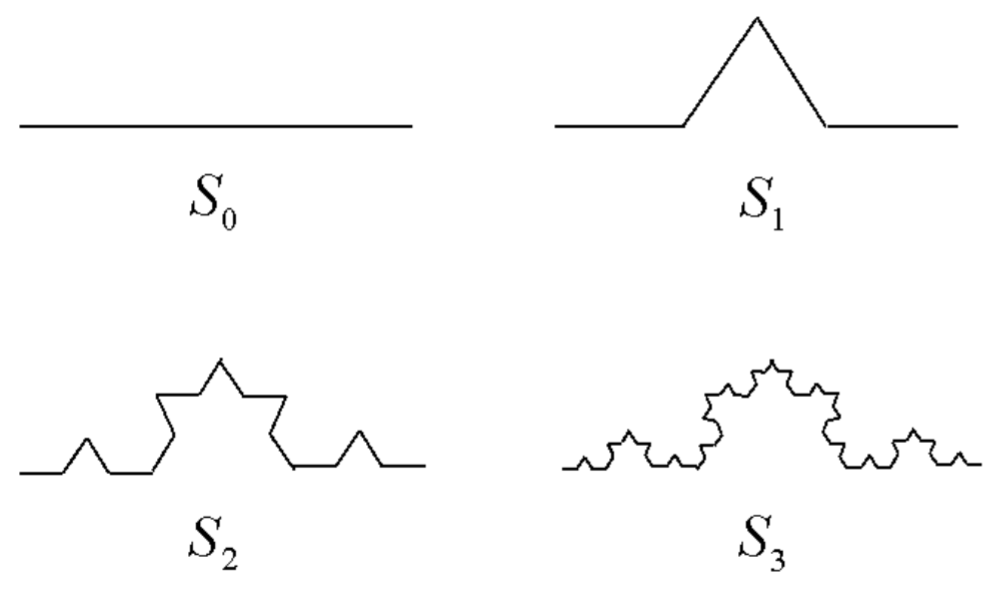
Aquí, la curva de Koch se compone de cuatro copias de sí misma escaladas por un factor de tres, de modo que
\[4=3^{D} \nonumber \]
y la dimensión de similitud es\(D=\log 4 / \log 3 \approx 1.2619 .\) La curva de Koch, por lo tanto, tiene una dimensión que se encuentra entre una línea y un área. En efecto, con cada iteración, la longitud de la curva de Koch aumenta en un factor de\(4 / 3\) para que su longitud sea infinita.
Copo de nieve Koch
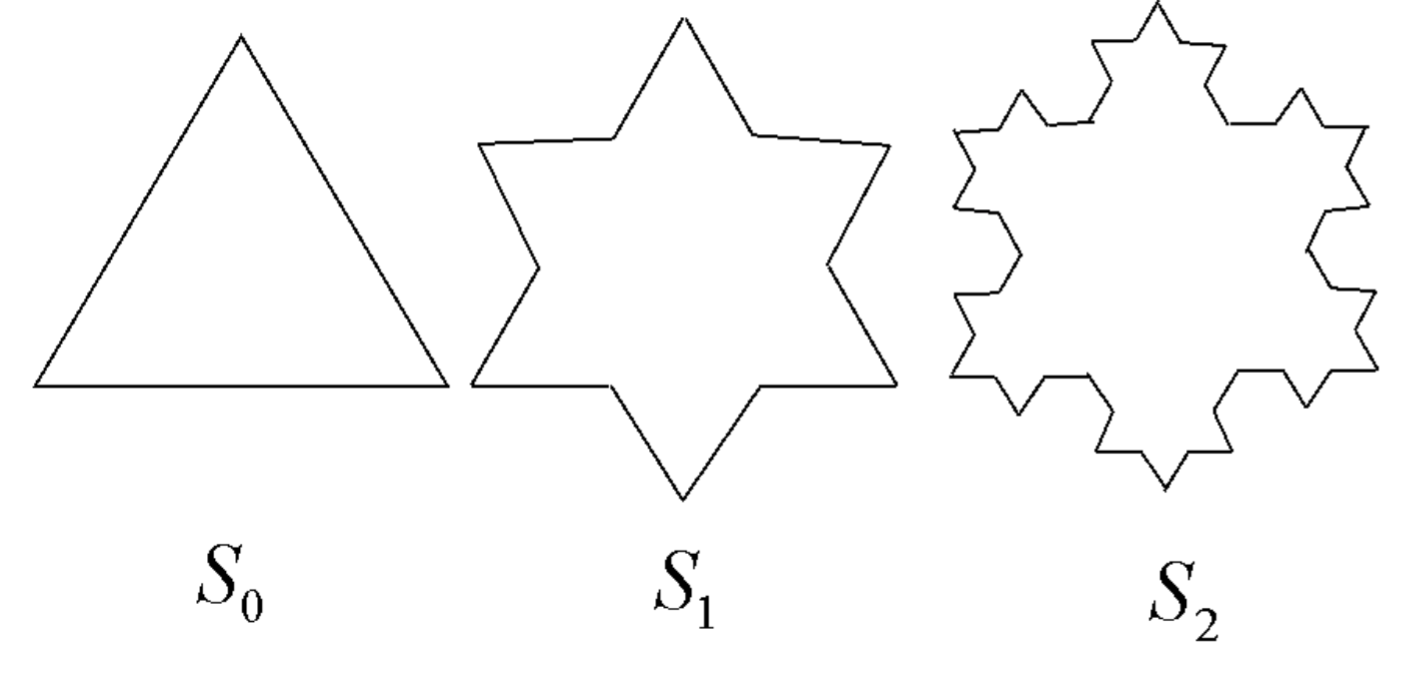
Aquí, comenzamos con un triángulo equilátero. Similar a la curva de Koch, reemplazamos el tercio medio de cada lado por dos segmentos de línea, como se ilustra en 12.9. El límite del copo de nieve de Koch tiene la misma dimensión fractal que la curva de Koch, y es de longitud infinita. Sin embargo, el área delimitada por el límite es obviamente finita y puede mostrarse que es\(8 / 5\) del área del triángulo original. Curiosamente, aquí un perímetro infinito encierra un área finita.
Dimensión de correlación
Estudios modernos de sistemas dinámicos han descubierto conjuntos llamados atractores extraños. Estos conjuntos comparten algunas de las características de los fractales clásicos: no son de relleno de espacio pero tienen estructura a escala arbitrariamente pequeña. Sin embargo, no son perfectamente autosimilares en el sentido de los fractales clásicos, habiendo surgido de la evolución caótica de algún sistema dinámico. Aquí, intentamos generalizar la definición de dimensión para que sea aplicable a atractores extraños y relativamente fácil de calcular. La definición y el algoritmo numérico aquí descritos fueron propuestos por primera vez en un artículo de Grassberger y Procaccia (1993)
Definiciones
Considera un conjunto\(S\) de\(N\) puntos. Denotar los puntos en este conjunto como\(\mathbf{x}_{i}\), con\(i=1,2, \ldots, N\) y denotar la distancia entre dos puntos\(\mathbf{x}_{i}\) y\(\mathbf{x}_{j}\) como\(r_{i j} .\) Tenga en cuenta que hay distancias\(N(N-1) / 2\) distintas. Definimos la correlación integral\(C(r)\) para ser
\[C(r)=\lim _{N \rightarrow \infty} \frac{2}{N(N-1)} \times\left\{\text { number of distinct distances } r_{i j} \text { less than } r\right\} . \nonumber \]
Si\(C(r) \propto r^{D}\) sobre un amplio rango de\(r\) cuándo\(N\) es suficientemente grande, entonces\(D\) se va a llamar la dimensión de correlación del conjunto\(S\). Tenga en cuenta que con esta normalización,\(C(r)=1\) para\(r\) mayor que la mayor distancia posible entre dos puntos en el conjunto\(S\).
La dimensión de correlación concuerda con la dimensión de similitud para un conjunto exactamente autosimilar. Como ejemplo específico, considere el conjunto Cantor. Supongamos que\(N\) los puntos que se encuentran en el conjunto de Cantor se eligen al azar para estar en\(S\). Dado que cada punto del set está a una distancia\(r=1\) de cada otro punto, uno tiene\(C(1)=1\). Ahora, aproximadamente la mitad de los puntos en se\(S\) encuentran entre 0 y\(1 / 3\), y la otra mitad se encuentran entre\(2 / 3\) y 1. Por lo tanto, sólo 1/2 de las distancias distintas posibles\(r_{i j}\) serán menores que\(1 / 3\) (as\(N \rightarrow \infty\)), de manera que eso\(C(1 / 3)=1 / 2\). Continuando con esta moda, encontramos en general eso\(C\left(1 / 3^{s}\right)=1 / 2^{s}\). Con\(r=1 / 3^{s}\), tenemos
\[s=-\frac{\log r}{\log 3} \nonumber \]
para que
\[\begin{aligned} C(r) &=2^{\log r / \log 3} \\ &=\exp (\log 2 \log r / \log 3) \\ &=r^{\log 2 / \log 3}, \end{aligned} \nonumber \]
válido para valores pequeños de\(r .\) Hemos encontrado así una dimensión de correlación,\(D=\log 2 / \log 3\), de acuerdo con la dimensión de similitud previamente determinada.
Computación numérica
Dado un conjunto finito\(S\) de\(N\) puntos, queremos formular un algoritmo numérico rápido para calcular\(C(r)\) en un rango suficientemente amplio de\(r\) para determinar con precisión la dimensión de correlación a\(D\) partir de una gráfica log-log de\(C(r)\) versus\(r .\) Un punto\(\mathbf{x}_{i}\) en el conjunto\(S\) puede ser un número real, o puede ser un par de coordenadas. Si los puntos provienen de una sección de Poincaré, entonces la dimensión fractal de la sección de Poincaré será una menor que la dimensión fractal real del atractor en el espacio de fase completo.
Defina la distancia\(r_{i j}\) entre dos puntos\(\mathbf{x}_{i}\) e\(\mathbf{x}_{j}\) in\(S\) para que sea la distancia euclidiana estándar. Para obtener un valor preciso de\(D\), es necesario desechar un transitorio inicial antes de acumular puntos para el conjunto\(S\). Ya que nos interesa una gráfica de\(\log C\) versus\(\log r\), calculamos\(C(r)\) en puntos\(r\) que están espaciados uniformemente en\(\log r .\) Por ejemplo, podemos calcular\(C(r)\) en los puntos \(r_{s}=2^{s}\), donde\(s\) toma valores enteros.
Primero, se cuenta el número de distancias distintas\(r_{i j}\) que se encuentran en el intervalo\(r_{s-1} \leq r_{i j}<r_{s}\). Denote este recuento por\(M(s)\). Luego se obtiene una aproximación a la integral de correlación\(C\left(r_{s}\right)\) utilizando\(N\) los puntos de datos de
\[C\left(r_{s}\right)=\frac{2}{N(N-1)} \sum_{s^{\prime}=-\infty}^{s} M\left(s^{\prime}\right) \nonumber \]
Se puede hacer uso de una función incorporada de MATLAB para acelerar el cálculo. La llamada a la función
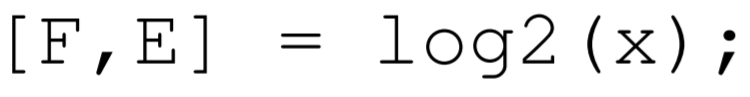
devuelve el número de punto flotante\(\mathrm{F}\) y el entero\(\mathrm{E}\) tal que\(\mathrm{x}=\mathrm{F} * 2^{\wedge} \mathrm{E}\), donde\(0.5 \leq|\mathrm{F}|<1\) y\(\mathrm{E}\) es un número entero. Para contar cada uno\(r_{i j}\) en el bin apropiado\(M(s)\), se pueden calcular todos los valores de\(r_{i j}\) y colocarlos en la matriz Matlab\(r\). Luego se utiliza la forma vectorial de\(10 \mathrm{~g} 2 . \mathrm{m}\) para calcular los valores correspondientes de\(s\):
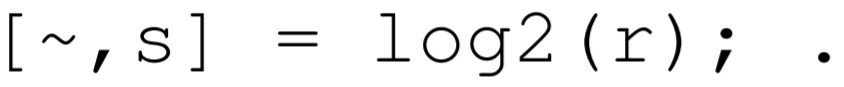
A continuación, se puede incrementar el recuento en una matriz Matlab\(M\) que corresponde a los valores enteros particulares de s. La función de Matlab cumsum.m se puede usar para calcular la matriz Matlab C.
Finalmente, se requiere un análisis de mínimos cuadrados de los datos para calcular la dimensión fractal\(D\). Al ver directamente la gráfica log-log, se puede elegir qué puntos adyacentes se ajustan a una línea recta y luego usar el método de mínimos cuadrados para calcular la pendiente. La función polyfit.m de MATLAB puede determinar la línea de mejor ajuste y la pendiente correspondiente. Idealmente, también se calcularía un error estadístico asociado a esta pendiente, y tal error debería ir a cero a medida que el número de puntos calculados se acerca al infinito.


