13: Dinámica del péndulo
- Page ID
- 117220
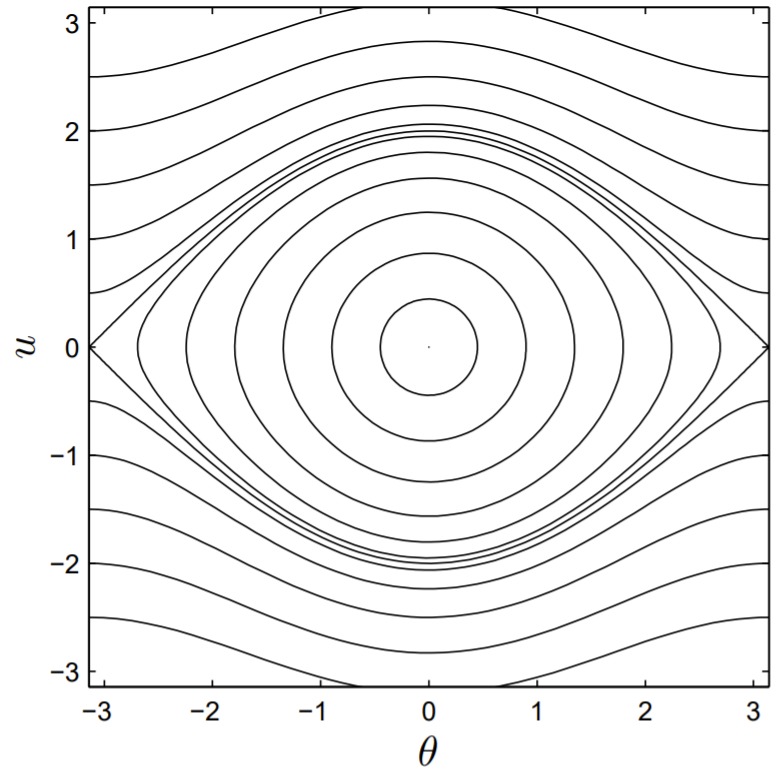
El péndulo no accionado tiene sólo un espacio bidimensional, formando un plano de fase donde es fácil visualizar los retratos de fase. El retrato de fase del péndulo simple de pequeña amplitud es particularmente fácil de dibujar. La forma adimensional de la ecuación de péndulo simple es
\[\ddot{\theta}+\theta=0, \nonumber \]
y las soluciones para\(\theta=\theta(t)\) y\(u=\dot{\theta}(t)\) son dadas por
\[\theta(t)=\theta_{m} \cos (t+\varphi), \quad u(t)=-\theta_{m} \sin (t+\varphi) \nonumber \]
El retrato de fase en el plano de\(\theta-u\) fase consiste en círculos concéntricos, con movimiento en sentido horario a lo largo de estos círculos, como se ve en los círculos de diámetro pequeño de la Fig. 13.1. A medida que aumenta la amplitud, la aproximación\(\sin \theta \approx \theta\) pierde validez, y la ecuación adimensional relevante se vuelve
\[\ddot{\theta}+\sin \theta=0 . \nonumber \]
Más allá de los círculos de diámetro pequeño de la Fig. 13.1, se observa que las líneas conectadas se alargan a\(u\) medida que aumenta la amplitud, lo que implica que el péndulo se ralentiza cuando la amplitud se vuelve grande (es decir, se alarga el período del péndulo). Finalmente, se dibuja una curva cerrada final, llamada separatriz, que separa el movimiento del péndulo de periódico a rotativo, correspondiendo este último movimiento a un péndulo que oscila sobre la parte superior en un movimiento circular. Exactamente en la trayectoria de la separatriz, el péndulo llega a descansar en el ángulo\(\pi\)\(180^{\circ}\), o, que es un punto fijo inestable del péndulo.
El péndulo simple es un sistema conservador, que exhibe una ley de conservación de la energía, y esto implica una conservación del área espacial de fase (o volumen). Si uno evoluciona con el tiempo un área inicial dada del espacio de fase de la Fig. 13.1, el área de este espacio de fase se conservará. Sin embargo, cuando se amortigua el péndulo, el área de este espacio de fase se encogerá a cero.
Cuenca de atracción del péndulo no accionado
Consideramos el péndulo amortiguado y no accionado con ecuación gobernante
\[\ddot{\theta}+\frac{1}{q} \dot{\theta}+\sin \theta=0 \nonumber \]
y el punto fijo estable dado por\((\theta, \dot{\theta})=(0,0)\). ¿Cómo podemos determinar la cuenca de atracción de este punto fijo? Por supuesto, con\(\dot{\theta}=0\), sólo los valores\(-\pi<\theta<\pi\) estarán en la cuenca de la atracción. Pero también necesitamos calcular la cuenca de atracción para valores iniciales distintos de cero de\(\dot{\theta}\).
Como suele ser el caso, para idear un algoritmo numérico lo mejor es apelar directamente a la física. Queremos encontrar el límite de las condiciones iniciales entre ya sea los atractivos puntos fijos\((0,0)\) y\((2 \pi, 0)\), o los atractivos puntos fijos\((0,0)\) y\((-2 \pi, 0)\). Las condiciones iniciales justo en el borde dan como resultado que el péndulo alcance los puntos fijos inestables\((\pi, 0)\) o\((-\pi, 0)\). Un pequeño
perturbación de\((\pi, 0)\) resultará en uno de los puntos atractivos\((0,0)\) o\((2 \pi, 0) ;\) de\((-\pi, 0)\), uno de los puntos atractivos\((0,0)\) o\((-2 \pi, 0)\).
El algoritmo luego inicializa el cálculo ya sea en el punto fijo inestable\((\pi, 0)\) o\((-\pi, 0)\), con una pequeña perturbación en la posición o velocidad que da como resultado que el punto de atracción final sea\((0,0)\). Podemos llamar a estos valores condiciones finales porque las ecuaciones diferenciales se integran entonces hacia atrás en el tiempo para determinar todas las condiciones iniciales posibles que puedan resultar en estas condiciones finales. Puedes convencerte de que las cuatro condiciones finales que se deben utilizar son las dos parejas\((\pi,-\epsilon),(\pi-\epsilon, 0)\), y\((-\pi, \epsilon),(-\pi+\epsilon, 0)\), con\(\epsilon\) muy pequeñas. El primero de cada par corresponde al movimiento inmediatamente anterior que es rotativo, y el segundo de cada par corresponde al movimiento inmediatamente anterior que es oscilatorio.
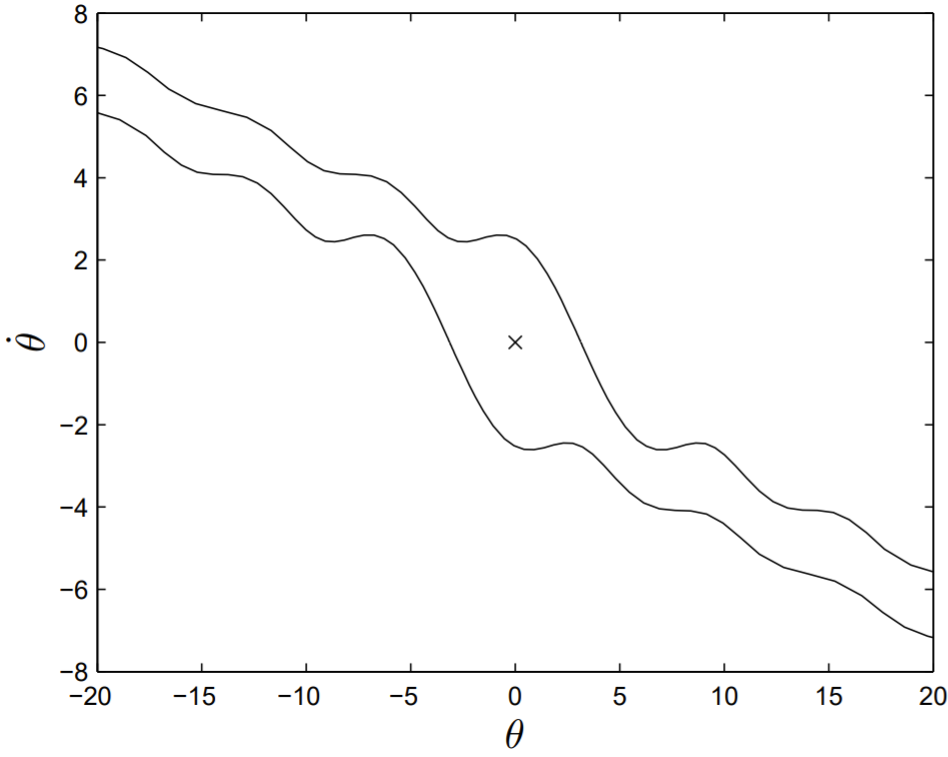
En la Fig. 13.2 se muestra una gráfica de las cuencas de atracción de\((0,0)\) for\(q=4\), correspondientes a un péndulo subamortiguado (la amortiguación crítica es\(q=1 / 2\)). El punto fijo atrayente está marcado por un\(x\) '', y la región dentro de las dos líneas curvas es la cuenca de atracción.
Bifurcación espontánea que rompe la simetría
Una interesante bifurcación supercrítica ocurre en las ecuaciones del péndulo, donde en el punto de bifurcación un ciclo límite estable se divide en dos. El ciclo de límite único muestra una simetría que ya no es respetada individualmente por los dos nuevos ciclos límite. Este tipo de bifurcación de horca es una manifestación de lo que se llama ruptura de simetría espontánea.
La ecuación del péndulo\((11.14)\), escrita de nuevo aquí, viene dada por
\[\ddot{\theta}+\frac{1}{q} \dot{\theta}+\sin \theta=f \cos \omega t . \nonumber \]
Usando\(\sin (-\theta)=-\sin \theta\) y\(\cos (\omega t-\pi)=-\cos \omega t\), la ecuación del péndulo se puede ver como invariante bajo la transformación
\[\theta \rightarrow-\theta, \quad t \rightarrow t-\pi / \omega \nonumber \]
con la interpretación física de que las ecuaciones de movimiento no hacen distinción entre los lados derecho e izquierdo de la vertical, consecuencia de la simetría tanto del péndulo como de la fuerza externa.
Consideremos nuevamente la solución asintótica de pequeña amplitud dada por\((11.10)\), que en variables adimensionales es
\[\theta(t)=\frac{f}{\sqrt{\left(1-\omega^{2}\right)^{2}+(\omega / q)^{2}}} \cos (\omega t+\phi), \nonumber \]
con
\[\tan \phi=\frac{\omega / q}{\omega^{2}-1} \nonumber \]
Podemos observar que esta solución también es invariante bajo\((13.6)\): la solución de pequeña amplitud obedece\(\theta(t)=-\theta(t-\pi / \omega) .\) Decimos que esta solución es simétrica, es decir, obedece a la misma simetría que las ecuaciones gobernantes; es decir, el movimiento del péndulo de pequeña amplitud es simétrico sobre la vertical.
también satisface (13.5) por el siguiente cálculo:
\[\begin{aligned} \ddot{\theta}_{2}(t)+\frac{1}{q} \dot{\theta}_{2}(t)+\sin \left(\theta_{2}(t)\right) &=-\ddot{\theta}_{1}(t-\pi / \omega)-\frac{1}{q} \dot{\theta}_{1}(t-\pi / \omega)-\sin \left(\theta_{1}(t-\pi / \omega)\right) \\ &=-f \cos (\omega t-\pi) \\ &=f \cos \omega t \end{aligned} \nonumber \]
Si las dos soluciones\(\theta_{1}(t)\) y\(\theta_{2}(t)\) son iguales, entonces decimos que esta solución es simétrica. Aquí, estamos considerando soluciones asintóticas que son independientes de las condiciones iniciales, ya que las propias condiciones iniciales también pueden romper la simetría. No obstante, si\(\theta_{1}(t)\) y no\(\theta_{2}(t)\) son iguales, decimos que estas soluciones son asimétricas, y que se ha producido una ruptura espontánea de simetría. Evidentemente, la ruptura espontánea de la simetría es un fenómeno decididamente no lineal. Después de que se produce la ruptura de simetría, las soluciones asimétricas deben ocurrir en pares, y el punto de bifurcación parece una bifurcación de horca, y puede ser súper o subcrítico. Cualquier bifurcación posterior que se le ocurra a una de las soluciones asimétricas también debe ser duplicada por la otra.
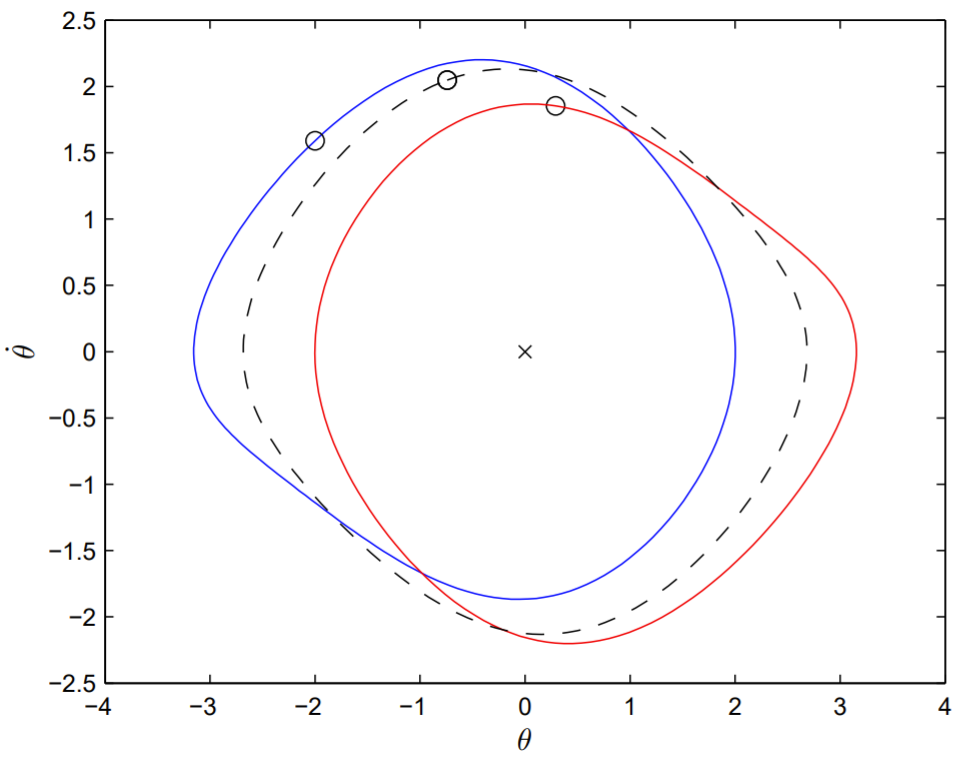
La ruptura espontánea de simetría ocurre en la dinámica del péndulo a los valores de los parámetros adimensionales\(f=1.5, \omega=2 / 3\), y aproximadamente\(q=1.246 .\) Por\(q\) poco menos de\(1.246\), la solución asintótica estable única para\(\theta=\theta(t)\) es simétrica , y por\(q\) apenas mayor que\(1.246\), existe un par de soluciones asintóticas estables que son asimétricas.
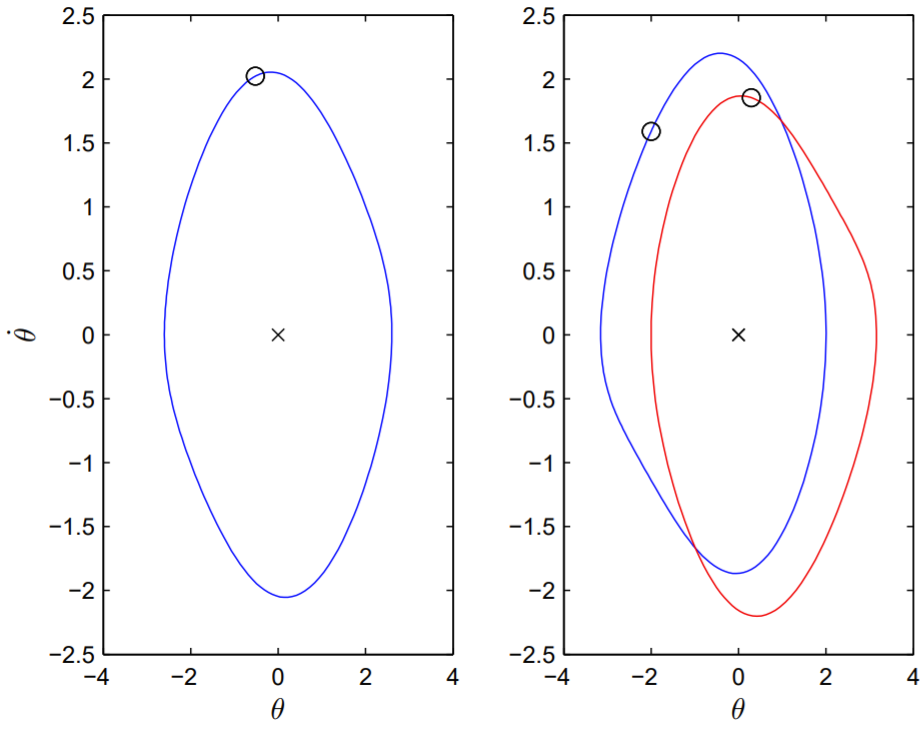
Al proyectar la trayectoria fase-espacio sobre el\(\theta-\dot{\theta}\) plano, en la Fig. \(13.3\)mostramos tanto la solución simétrica cuándo como\(q=1.24\) las dos soluciones asimétricas cuándo\(q=1.30\). Para observar explícitamente la simetría de las soluciones, marcamos el valor de\((\theta, \theta)\) en el momento\(t=\)\(n 2 \pi / \omega\), con\(n\) un entero positivo (equivalente al tiempo\(t=0)\), y el valor de\((-\theta,-\dot{\theta})\) al tiempo\(t=n 2 \pi / \omega+\pi / \omega\) (equivalente al tiempo\(t=\pi / \omega\)). Para una solución simétrica, estos dos puntos marcan el mismo punto en la trayectoria, y para soluciones asimétricas marcan puntos en diferentes trayectorias. Observe que después de la ocurrencia de la ruptura de simetría, una de las soluciones asintóticas sufre una oscilación centrada a la derecha de la vertical, y la otra, centrada a la izquierda.
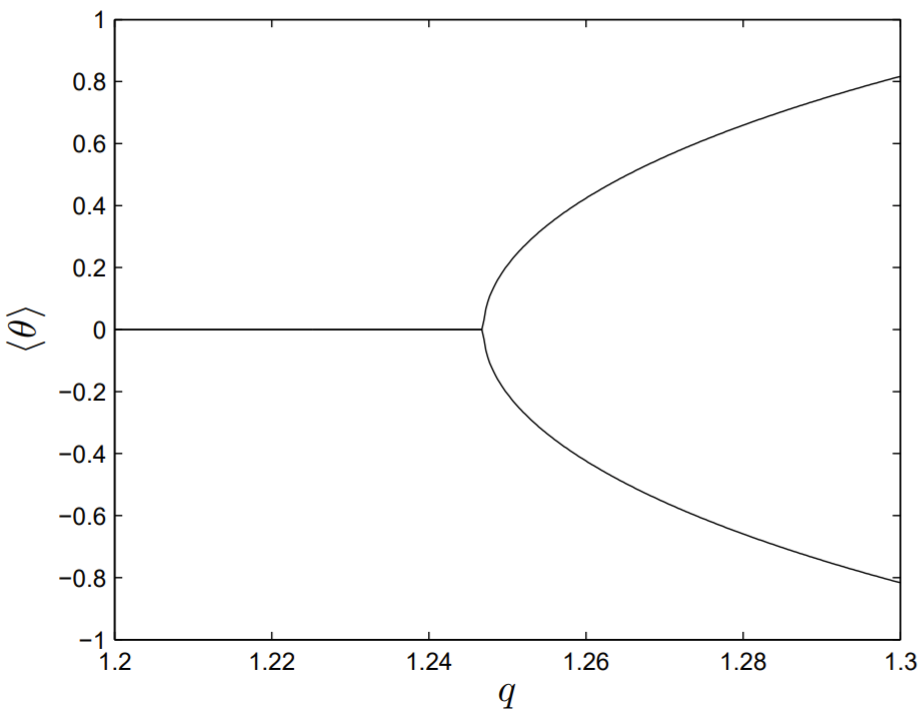
Podemos graficar un diagrama de bifurcación asociado a la ruptura de simetría de las soluciones. Arreglamos\(f=1.5\)\(\omega=2 / 3\) y variamos\(q\) a través del punto de bifurcación\(q=1.246\). Necesitamos distinguir los ciclos límite simétricos de los asimétricos, y un método es calcular el valor promedio de\(\theta(t)\) más de un período de oscilación; es decir,
\[\langle\theta\rangle=\frac{1}{T} \int_{0}^{T} \theta d t \nonumber \]
donde\(T=2 \pi / \omega .\) Para la solución simétrica,\(\langle\theta\rangle=0\), mientras que\(\langle\theta\rangle\) adquiere valores tanto positivos como negativos después de que se produce la ruptura de simetría. En la Fig. 13.4, trazamos el valor de\(\langle\theta\rangle\) versus\(q\). A un valor de aproximadamente\(q=1.246\), se produce una ruptura espontánea de simetría y el ciclo de límite simétrico estable se divide en dos ciclos de límite asimétricos, en lo que evidentemente es una bifurcación supercrítica de horca.
El ciclo límite simétrico aún existe después del punto de bifurcación, y aunque inestable, también se puede calcular. Para calcular el ciclo inestable, se podrían determinar los valores de\(\theta\) y\(\dot{\theta}\) en\(t=0\) ese momento se encuentran en este ciclo, y luego integrarse a lo largo de un período (durante el cual la inestabilidad no tiene tiempo suficiente para desarrollarse). El problema de determinar las condiciones iniciales correctas se puede plantear como un problema en el hallazgo multidimensional de raíces. La idea clave es que un ciclo de límite simétrico satisfaga\(\theta(t)=-\theta(t-\pi / \omega)\). Por lo tanto, determinamos el vector de solución de las condiciones iniciales\((\theta(0), \theta(0))\) que satisface las dos ecuaciones
\[\begin{aligned} &\theta(0)+\theta(\pi / \omega)=0 \\ &\dot{\theta}(0)+\dot{\theta}(\pi / \omega)=0 \end{aligned} \nonumber \]
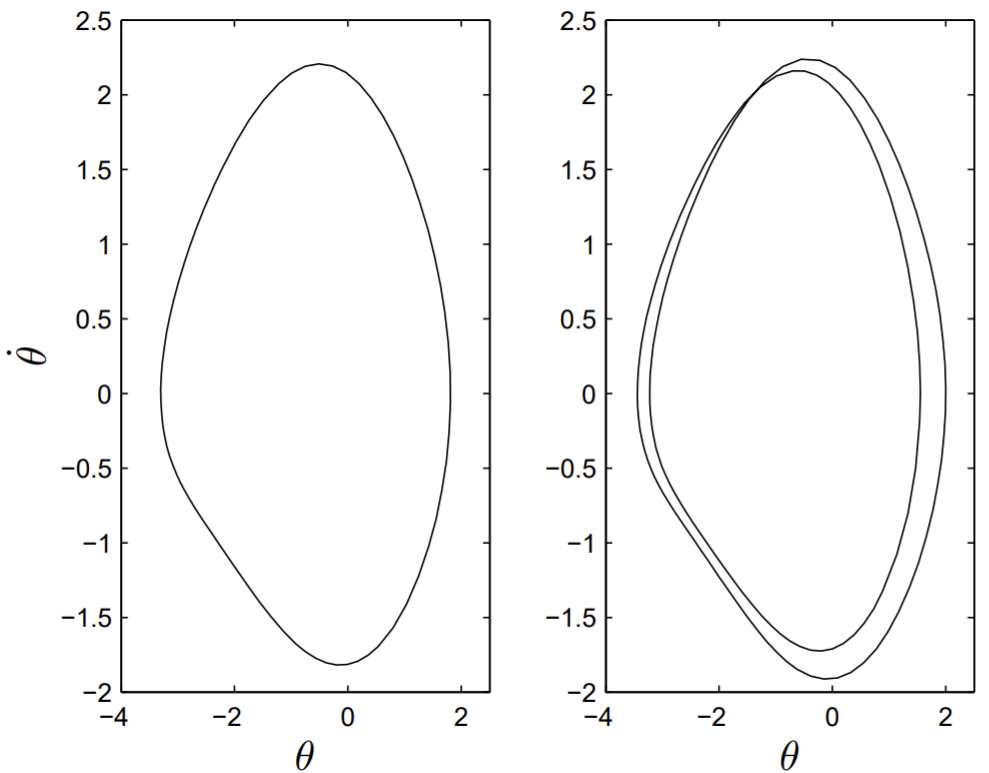
donde\(\theta(\pi / \omega)\) y\(\dot{\theta}(\pi / \omega)\) se determinan integrando a partir de\(t=0\) las ecuaciones diferenciales usando ode\(45 . \mathrm{m}\) con las condiciones iniciales\((\theta(0), \dot{\theta}(0))\). El hallazgo de raíces se puede hacer usando una versión bidimensional de la regla secante o, más simplemente, la función incorporada de MATLAB fsolve.m La convergencia a las raíces es robusta, y una suposición inicial para las raíces se puede tomar, por ejemplo, como\((\theta(0), \dot{\theta}(0))=(0,0)\). Una gráfica de los dos ciclos de límite asimétrico estable, y el ciclo límite simétrico inestable cuando\(f=1.5, \omega=2 / 3\) y\(q=1.3\) se muestra en la Fig. 13.5.
Bifurcaciones de duplicación de períodos
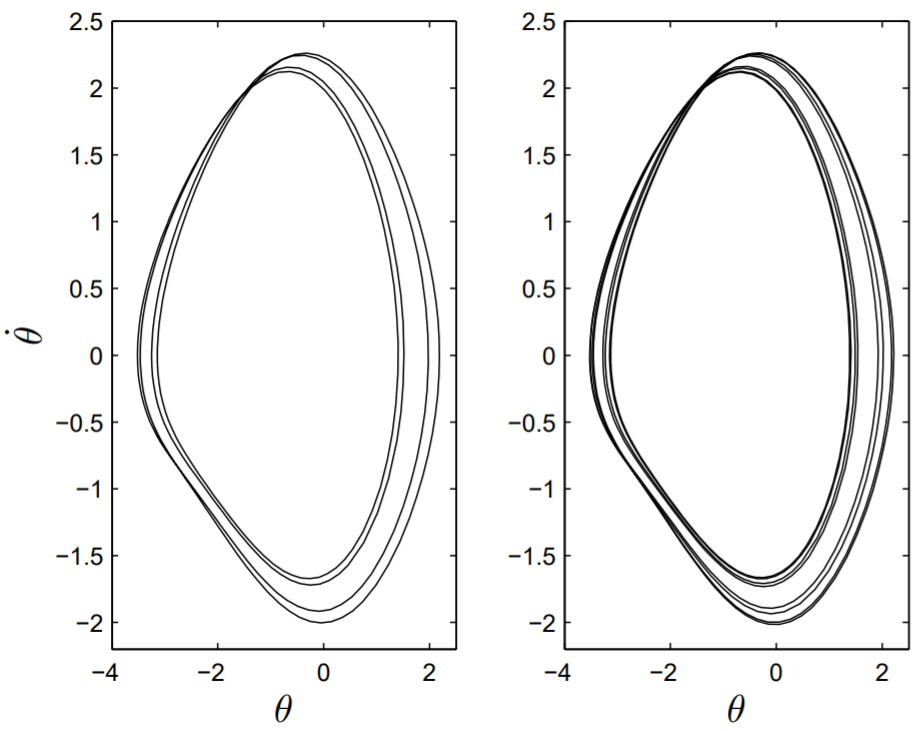
Las bifurcaciones de duplicación de períodos continúan con el aumento\(q\). La segunda duplicación del período dos al período cuatro ocurre aproximadamente\(q=1.370\) y la tercera duplicación del período cuatro al período ocho ocurre aproximadamente\(q=1.375\). Las proyecciones\(\theta-\dot{\theta}\) fase-espacio para el periodo cuatro y ocho se muestran en la Fig. 13.8.
Se puede trazar un diagrama de bifurcación que ilustra estas bifurcaciones de duplicación de períodos. Utilizamos una sección de Poincaré para trazar el valor de\(\theta\) en los tiempos correspondientes a\(2 \pi n / \omega\), con\(n\) un entero. El parámetro de control para la bifurcación es\(q\), y en la Fig. 13.9, trazamos el diagrama de bifurcación para\(1.34<q<1.38\). En general, el ángulo\(\theta\) debe mapearse en el intervalo\(-\pi<\)\(\theta<\pi\), pero para estos valores de parámetros no hay movimiento giratorio. Se observan bifurcaciones de duplicación de períodos y eventualmente el péndulo se vuelve aperiódico. También son aparentes ventanas adicionales de periodicidad en\(q\) las regiones aperiódicas de.
El comportamiento aperiódico del péndulo observado en la Fig. \(13.9\)corresponde a un péndulo caótico. Si tan solo el péndulo exhibiera la ruta de duplicación de período hacia el caos, entonces los resultados mostrados en la Fig. 13.9, aunque interesantes, serían de menor importancia. Pero de hecho muchos otros sistemas no lineales también exhiben esta ruta hacia el caos, y hay algunas características universales de la Fig. \(13.9\), descubierto por primera vez por Feigenbaum en 1975. Una de estas características se llama ahora la constante Feigenbaum,\(\delta\)
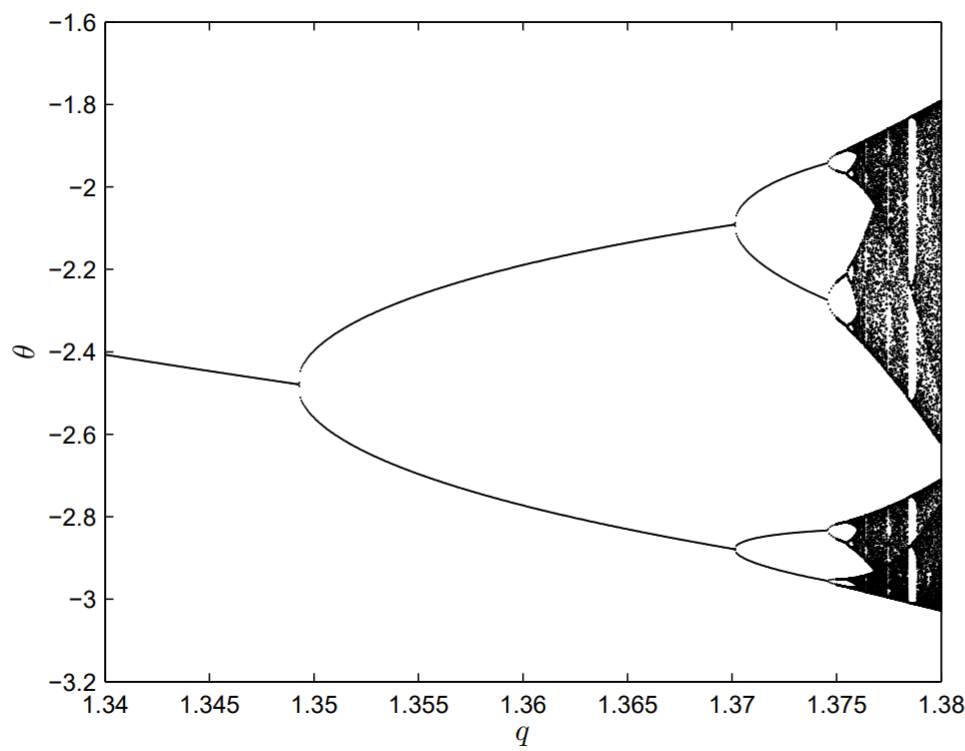
Tenga en cuenta que para el péndulo, ya podemos calcular
\[\delta_{1}=\frac{1.370-1.348}{1.375-1.370}=4.400 \nonumber \]
El significado de se\(\delta\) puede dilucidar mejor por escrito
\[q_{n+2}-q_{n+1}=\frac{q_{n+1}-q_{n}}{\delta_{n}} \nonumber \]
y al continuar iterando esta ecuación, obtenemos
\[q_{n+2}-q_{n+1}=\frac{q_{2}-q_{1}}{\delta_{1} \delta_{2} \cdots \delta_{n}} . \nonumber \]
Con todos los\(\delta_{n}\)'s aproximadamente iguales a\(\delta\), entonces tenemos el escalado
\[q_{n+2}-q_{n+1} \propto \delta^{-n} \nonumber \]
Un\(\delta\) mayor que uno aseguraría entonces que las bifurcaciones ocurren cada vez más juntas, de manera que finalmente se alcanza un periodo infinito (y caos). El valor de se\(\delta\) puede calcular con alta precisión y se ha encontrado que es
\[\delta=4.669201609102990 \ldots, \nonumber \]
y nuestro valor de\(\delta_{1}=4.4\) es una aproximación aproximada.
Duplicación de periodos en el mapa logístico
Feigenbaum descubrió originalmente la ruta de duplicación de períodos hacia el caos mediante el estudio de un simple mapa onedimensional. Un mapa unidimensional con un solo parámetro de control se\(\mu\) puede escribir como
\[x_{n+1}=f_{\mu}\left(x_{n}\right) \nonumber \]
donde\(f_{\mu}(x)\) hay alguna función especificada. Se itera un mapa unidimensional, comenzando con algún valor inicial\(x_{0}\), para obtener la secuencia\(x_{1}, x_{2}, x_{3}, \ldots .\) Si la secuencia converge a\(x_{*}\), entonces\(x_{*}\) es un punto fijo estable del mapa.
El mapa unidimensional específico que estudiaremos aquí es el mapa logístico, con
\[f_{\mu}(x)=\mu x(1-x) \nonumber \]
El mapa logístico es quizás la ecuación no lineal más simple que exhibe la ruta de duplicación de período hacia el caos. Para limitar los valores de\(x_{n}\) estar entre cero y unidad, asumimos eso\(0<\mu<4\) y aquello\(0<x_{0}<1\).
Un ciclo de período-1 para el mapa logístico corresponde a un punto fijo estable. Los puntos fijos estables son soluciones de la ecuación\(x=f_{\mu}(x)\), o
\[x=\mu x(1-x) . \nonumber \]
Las dos soluciones están dadas por\(x_{*}=0\) y\(x_{*}=1-1 / \mu\). El primer punto fijo\(x_{*}=0\) debe ser estable para\(0<\mu<1\), siendo el único punto fijo que se encuentra entre cero y uno que existe en este rango. Para determinar la estabilidad del segundo punto fijo, se hace uso del análisis de estabilidad lineal discutido en\(\S 12.1\).
Para un mapa unidimensional,\(x_{*}\) es un punto fijo estable de\((13.17)\) si\(\left|f_{\mu}^{\prime}\left(x_{*}\right)\right|<1 .\) Para el mapa logístico dado por (13.18), por\(f_{\mu}^{\prime}(0)=\mu\) lo que\(x_{*}=0\) es estable para\(0<\mu<1\) como ya hemos supuesto, y para el segundo punto fijo
\[f_{\mu}^{\prime}(1-1 / \mu)=2-\mu . \nonumber \]
Por lo tanto, encontramos que\(x_{*}=1-1 / \mu\) es estable para\(1<\mu<3\).
¿Qué sucede cuando\(\mu\) llega a ser mayor de tres? Ahora mostraremos que el primer períododuplicando la bifurcación ocurre en\(\mu=3\). Debido a la simplicidad del mapa logístico, podemos determinar explícitamente el ciclo del período-2. Considere el siguiente mapa compuesto:
\[g_{\mu}(x)=f_{\mu}\left(f_{\mu}(x)\right) \nonumber \]
Los puntos fijos de este mapa consistirán tanto en ciclos de período-1 como de ciclos de período-2 del mapa original (13.18). Si\(x=x_{*}\) es un punto fijo del mapa compuesto (13.21), entonces\(x_{*}\) satisface la ecuación
\[x=g_{\mu}(x) \nonumber \]
Un ciclo de período-2 del mapa corresponde\(f_{\mu}(x)\) necesariamente a dos puntos fijos distintos del mapa compuesto (13.21). Denotamos estos dos puntos fijos por\(x_{0}\) y\(x_{1}\), que satisfacen
\[x_{1}=f_{\mu}\left(x_{0}\right), \quad x_{0}=f_{\mu}\left(x_{1}\right) . \nonumber \]
Llamaremos a\(x_{0}, x_{1}\) la órbita del ciclo del período-2, con la generalización posterior de la llamada\(x_{0}, x_{1}\),\(\ldots, x_{2^{n}}-1\) la órbita del\(-2^{n}\) ciclo de periodo.
El ciclo del período-2 ahora se puede determinar analíticamente resolviendo
\[\begin{aligned} x &=f_{\mu}\left(f_{\mu}(x)\right) \\ &=f_{\mu}(\mu x(1-x)) \\ &=\mu(\mu x(1-x))(1-\mu x(1-x)) \end{aligned} \nonumber \]
que es una ecuación cuártica para\(x\). Se conocen dos soluciones correspondientes a ciclos de período-1:\(x_{*}=0\) y\(x_{*}=1-1 / \mu\). La factorización de estas dos soluciones, la segunda mediante el uso de división larga, da como resultado la ecuación cuadrática dada por
\[\mu^{2} x^{2}-\mu(\mu+1) x+(\mu+1)=0 . \nonumber \]
El ciclo del período-2, entonces, corresponde a las dos raíces de esta ecuación cuadrática; es decir,
\[x_{0}=\frac{1}{2 \mu}((\mu+1)+\sqrt{(\mu+1)(\mu-3)}), \quad x_{1}=\frac{1}{2 \mu}((\mu+1)-\sqrt{(\mu+1)(\mu-3)}) . \nonumber \]
Estas raíces son soluciones válidas para\(\mu \geq 3\). Exactamente a\(\mu=3\), el ciclo del período-2 satisface\(x_{0}=x_{1}=\)\(2 / 3\), que coincide con el valor del ciclo del período-1\(x_{*}=1-1 / \mu=2 / 3 .\) At\(\mu=3\), entonces, esperamos que el punto fijo del mapa compuesto correspondiente a un ciclo del período-1 vaya inestable a través de una bifurcación de tridente supercrítica a un par de puntos fijos estables, correspondientes a un ciclo de período-2.
¿Cuándo se vuelve inestable este ciclo del período-2? En\(\mu=3\) y\(x_{*}=2 / 3\), tenemos
\[\begin{aligned} f_{\mu}^{\prime}\left(x_{*}\right) &=\mu\left(1-2 x_{*}\right) \\ &=-1, \end{aligned} \nonumber \]
de manera que el ciclo del período-1 se vuelve inestable cuando la derivada de la función map alcanza el valor de\(-1\), y es razonable esperar que el ciclo del período-2 también se vuelva inestable cuando
\[g_{\mu}^{\prime}\left(x_{0}\right)=-1, \quad g_{\mu}^{\prime}\left(x_{1}\right)=-1 . \nonumber \]
Ahora,
\[\begin{aligned} g_{\mu}^{\prime}\left(x_{0}\right) &=f_{\mu}^{\prime}\left(f_{\mu}\left(x_{0}\right)\right) f_{\mu}^{\prime}\left(x_{0}\right) \\ &=f_{\mu}^{\prime}\left(x_{1}\right) f_{\mu}^{\prime}\left(x_{0}\right), \end{aligned} \nonumber \]
y
\[\begin{aligned} g_{\mu}^{\prime}\left(x_{1}\right) &=f_{\mu}^{\prime}\left(f_{\mu}\left(x_{1}\right)\right) f_{\mu}^{\prime}\left(x_{1}\right) \\ &=f_{\mu}^{\prime}\left(x_{0}\right) f_{\mu}^{\prime}\left(x_{1}\right) . \end{aligned} \nonumber \]
Las dos ecuaciones de\((13.26)\) son, por lo tanto, idénticas, y el ciclo del período-2 irá inestable al valor de\(\mu\) satisfacer
\[f_{\mu}^{\prime}\left(x_{0}\right) f_{\mu}^{\prime}\left(x_{1}\right)=-1 \nonumber \]
donde\(x_{0}\) y\(x_{1}\) están dadas por (13.25).
La ecuación para\(\mu\), entonces, viene dada por
\[\mu^{2}\left(1-2 x_{0}\right)\left(1-2 x_{1}\right)=-1 \nonumber \]
O
\[\mu^{2}\left(1-2\left(x_{0}+x_{1}\right)+4 x_{0} x_{1}\right)+1=0 \nonumber \]
Ahora, desde (13.25),
\[x_{0}+x_{1}=\frac{\mu+1}{\mu}, \quad x_{0} x_{1}=\frac{\mu+1}{\mu^{2}} . \nonumber \]
Sustitución de (13.30) en (13.29) resultados, después de la simplificación, en la ecuación cuadrática
\[\mu^{2}-2 \mu-5=0, \nonumber \]
con la única solución positiva dada por
\[\begin{aligned} \mu &=1+\sqrt{6} \\ & \approx 3.449490 . \end{aligned} \nonumber \]
Por lo tanto, esperamos que el ciclo del período-2 se bifurque a un ciclo del período-4 en\(\mu \approx 3.449490\).
CAPÍTULO 13. DINÁMICA DE PÉNDULO
| \(n\) | \(\mu_{n}\) |
|---|---|
| \ (n\)” style="text-align:left; ">1 | \ (\ mu_ {n}\)” style="text-align:left; ">3 |
| \ (n\)” style="text-align:left; ">2 | \ (\ mu_ {n}\)” style="text-align:left; ">\(3.449490 \ldots\) |
| \ (n\)” style="text-align:left; ">3 | \ (\ mu_ {n}\)” style="text-align:left; ">\(3.544090 \ldots\) |
| \ (n\)” style="text-align:left; ">4 | \ (\ mu_ {n}\)” style="text-align:left; ">\(3.564407 \ldots\) |
| \ (n\)” style="text-align:left; ">5 | \ (\ mu_ {n}\)” style="text-align:left; ">\(3.568759 \ldots\) |
| \ (n\)” style="text-align:left; ">6 | \ (\ mu_ {n}\)” style="text-align:left; ">\(3.569692 \ldots\) |
| \ (n\)” style="text-align:left; ">7 | \ (\ mu_ {n}\)” style="text-align:left; ">\(3.569891 \ldots\) |
| \ (n\)” style="text-align:left; ">8 | \ (\ mu_ {n}\)” style="text-align:left; ">\(3.569934 \ldots\) |
Cuadro 13.1: Los primeros ocho valores\(\mu_{n}\) en los que ocurren las bifurcaciones de duplicación de período.
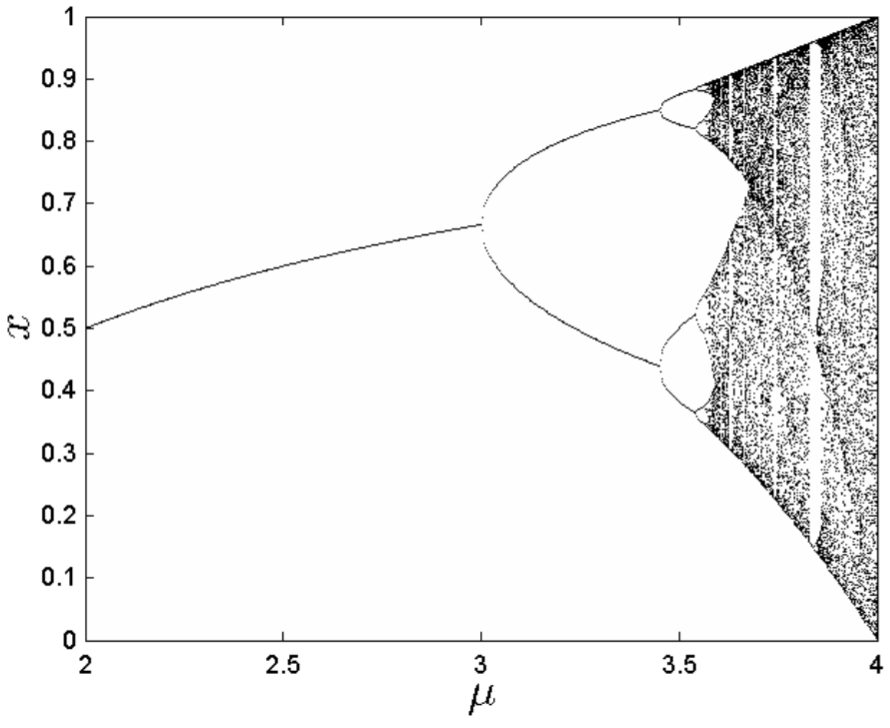
Si\(\mu_{n}\) definimos que es el valor\(\mu\) al que el\(^{n-1}\) ciclo del período-2 se bifurca a un\(^{n}\) ciclo del período-2, entonces hemos determinado analíticamente eso\(\mu_{1}=3\) y\(\mu_{2}=1+\sqrt{6}\). Enumeramos en la Tabla 13.1, los primeros ocho valores aproximados de\(\mu_{n}\), calculados numéricamente.
Podemos calcular un diagrama de bifurcación para el mapa logístico. Para\(2<\mu<4\), trazamos las iteraciones del mapa, descartando transitorios iniciales. El diagrama de bifurcación se muestra en la Fig. 13.10. Observe la extraña similitud entre el diagrama de bifurcación para el mapa logístico, y el que hemos calculado previamente para la ecuación de péndulo impulsado y amortiguado, Fig. \(13.9 .\)Obsérvese también que el cálculo de la Fig. 13.10, siendo del orden de segundos, es sustancialmente más rápido que el de la Fig. 13.9, que tardó alrededor de una hora, debido a que un mapa unidimensional es mucho más rápido de calcular que la sección Poincaré de un par de ecuaciones diferenciales acopladas de primer orden.
Computación de la constante de Feigenbaum
La duplicación de períodos en el mapa logístico permite un cálculo preciso de la constante de Feigenbaum\(\delta\), definida como
\[\delta=\lim _{n \rightarrow \infty} \delta_{n} \nonumber \]
donde
\[\delta_{n}=\frac{\mu_{n+1}-\mu_{n}}{\mu_{n+2}-\mu_{n+1}} \nonumber \]
En la\(13.1\) tabla se enumeran los primeros ocho valores conocidos de\(\mu_{n}\) en los puntos de bifurcación. Estos valores, y aquellos a valores aún mayores de\(n\), son de hecho muy difíciles de calcular con alta precisión debido a la lenta convergencia de las iteraciones en los puntos de bifurcación. Más bien, vamos a calcular los valores de\(\mu\) a lo que se llaman ciclos superestables. Este ahora conocido método para la computación\(\delta\) fue descrito por primera vez por Keith Briggs (1989).
Recordemos que para el mapa unidimensional general
\[x_{n+1}=f_{\mu}\left(x_{n}\right), \nonumber \]
una perturbación\(\epsilon_{n}\) a un punto fijo\(x_{*}\) decae como
\[\epsilon_{n+1}=f_{\mu}^{\prime}\left(x_{*}\right) \epsilon_{n} . \nonumber \]
En un llamado punto fijo superestable, sin embargo,\(f_{\mu}^{\prime}\left(x_{*}\right)=0\) y la perturbación decae mucho más rápido como
\[\epsilon_{n+1}=\frac{1}{2} f_{\mu}^{\prime \prime}\left(x_{*}\right) \epsilon_{n}^{2} . \nonumber \]
¿Cuáles son los puntos fijos superestables del mapa logístico? Ahora bien, los valores\(x_{i}\) que están en la órbita de un\(-2^{n}\) ciclo de periodo son puntos fijos del mapa compuesto
\[x_{n+1}=g_{\mu}\left(x_{n}\right), \nonumber \]
donde\(g_{u}=f_{u} \circ f_{u} \circ \cdots \circ f_{u}\), donde la composición se repite\(2^{n}\) veces. La órbita de un ciclo superestable, entonces, consiste en puntos fijos superestables de\((13.37)\). Si el\(2^{n}\) ciclo de periodo tiene órbita\(x_{0}, x_{1}, \ldots, x_{2^{n}-1}\), nosotros tenemos\(f_{\mu}\left(x_{0}\right)=x_{1}, f_{\mu}\left(x_{1}\right)=x_{2}, \ldots, f_{\mu}\left(x_{2^{n}-1}\right)=x_{0}\), y por la regla de la cadena,
\[g_{\mu}^{\prime}\left(x_{i}\right)=f_{\mu}^{\prime}\left(x_{0}\right) f_{\mu}^{\prime}\left(x_{1}\right) \cdots f_{\mu}^{\prime}\left(x_{2^{n}-1}\right), \nonumber \]
para todos\(x_{i}\) en la órbita del período-\(2^{n}\) ciclo. Con
\[f_{\mu}^{\prime}(x)=\mu(1-2 x) \nonumber \]
tenemos\(g_{\mu}^{\prime}(x)=0\) para\(x=1 / 2\). Por lo tanto\(x_{0}=1 / 2\), si, digamos, está en la órbita de un período-\(2^{n}\) ciclo, entonces este ciclo es superestable. En el punto de bifurcación creando un\(^{n}\) ciclo de período-2, el ciclo tiene estabilidad marginal y\(g_{\mu}^{\prime}\left(x_{0}\right)=1 .\) As\(\mu\) aumenta,\(g_{\mu}^{\prime}\left(x_{0}\right)\) disminuye, y eventualmente el\(^{n}\) ciclo del período-2 pierde estabilidad cuando \(g_{\mu}^{\prime}\left(x_{0}\right)=-1\). En algún valor intermedio de\(\mu\), entonces, existe un valor de\(x_{0}\) con\(g_{\mu}^{\prime}\left(x_{0}\right)=0\), y aquí podemos asignar\(x_{0}=1 / 2 .\) Por lo tanto, cada período-\(2^{n}\) ciclo contiene un valor de\(\mu\) para el cual \(x_{0}=1 / 2\)está en la órbita del ciclo.
En consecuencia,\(m_{n}\) definimos como el valor de\(\mu\) al que\(x_{0}=1 / 2\) se encuentra en la órbita del período-\(2^{n}\) ciclo. Podemos modificar la definición de la constante de Feigenbaum (13.33) para ser
\[\delta_{n}=\frac{m_{n+1}-m_{n}}{m_{n+2}-m_{n+1}} . \nonumber \]
Aunque los valores de\(\delta_{n}\) computados a partir de (13.33) y (13.40) diferirán ligeramente, los valores como\(n \rightarrow \infty\) deberían ser los mismos.
Podemos determinar fácilmente los dos primeros valores de\(m_{n}\). Para el ciclo del período-1, tenemos
\[\frac{1}{2}=m_{0} \frac{1}{2}\left(1-\frac{1}{2}\right) \nonumber \]
o bien\(m_{0}=2\), como se confirma a partir de la Fig. 13.10. Para determinar\(m_{1}\), hacemos uso del ciclo del período-2 dado por\((13.21)\), y la Fig. \((13.10)\), lo que demuestra que la raíz más pequeña pasa a través\(x_{0}=1 / 2\). Por lo tanto,
\[\frac{1}{2}=\frac{1}{2 m_{1}}\left(\left(m_{1}+1\right)-\sqrt{\left(m_{1}+1\right)\left(m_{1}-3\right)}\right) ; \nonumber \]
y resolviendo para\(m_{1}\), obtenemos la ecuación cuadrática
\[m_{1}^{2}-2 m_{1}-4=0 \nonumber \]
con solución\(m_{1}=1+\sqrt{5} \approx 3.2361\). Otros valores de\(m_{n}\) serán calculados numéricamente.
Para determinar\(m_{n}\), necesitamos resolver la ecuación\(G(\mu)=0\), donde
\[G(\mu)=g_{\mu}(1 / 2)-\frac{1}{2} \nonumber \]
y donde como antes,\(g_{\mu}(x)\) es la composición de\(2^{n}\) tiempos\(f_{\mu}(x)\) repetidos. Las raíces de (13.44) están dadas por\(m_{0}, m_{1}, \ldots m_{n}\), de manera que la raíz deseada es la más grande.
Utilizaremos el método de Newton,\(\S 2.2\), para resolver (13.44). Para implementar el método de Newton, necesitamos calcular ambos\(G(\mu)\) y\(G^{\prime}(\mu)\). Definir\(N=2^{n}\). Luego usando el mapa logístico
\[x_{n+1}=\mu x_{n}\left(1-x_{n}\right), \nonumber \]
e iterando con\(x_{0}=1 / 2\), obtenemos\(x_{1}, x_{2}, \ldots, x_{N} .\) Esta órbita es superestable si\(x_{N}=1 / 2\). Por lo tanto, tenemos
\[G(\mu)=x_{N}-1 / 2 \nonumber \]
Además,
\[G^{\prime}(\mu)=x_{N^{\prime}}^{\prime} \nonumber \]
donde el derivado es con respecto a\(\mu\). Desde (13.45), tenemos
\[\begin{aligned} x_{n+1}^{\prime} &=x_{n}\left(1-x_{n}\right)+\mu x_{n}^{\prime}\left(1-x_{n}\right)-\mu x_{n} x_{n}^{\prime} \\ &=x_{n}\left(1-x_{n}\right)+\mu x_{n}^{\prime}\left(1-2 x_{n}\right) . \end{aligned} \nonumber \]
Ya que siempre elegimos\(x_{0}=1 / 2\), independientemente de\(\mu\), tenemos como valor inicial\(x_{0}^{\prime}=0 .\) Por lo tanto, para calcular ambos\(x_{N}\) e\(x_{N^{\prime}}^{\prime}\) iterar\(2^{n}\) veces las ecuaciones del mapa acoplado
\[\begin{aligned} &x_{n+1}=\mu x_{n}\left(1-x_{n}\right) \\ &x_{n+1}^{\prime}=x_{n}\left(1-x_{n}\right)+\mu x_{n}^{\prime}\left(1-2 x_{n}\right) \end{aligned} \nonumber \]
| \(n\) | \(m_{n}\) | \(\delta_{n}\) |
|---|---|---|
| \ (n\)” style="text-align:left; ">0 | \ (m_ {n}\)” style="text-align:left; ">2 | \ (\ delta_ {n}\)” style="text-align:left; ">\(4.7089430135405\) |
| \ (n\)” style="text-align:left; ">1 | \ (m_ {n}\)” style="text-align:left; ">\(1+\sqrt{5}\) | \ (\ delta_ {n}\)” style="text-align:left; ">\(4.6807709980107\) |
| \ (n\)” style="text-align:left; ">2 | \ (m_ {n}\)” style="text-align:left; ">\(3.4985616993277\) | \ (\ delta_ {n}\)” style="text-align:left; ">\(4.6629596111141\) |
| \ (n\)” style="text-align:left; ">3 | \ (m_ {n}\)” style="text-align:left; ">\(3.5546408627688\) | \ (\ delta_ {n}\)” style="text-align:left; ">\(4.6684039259164\) |
| \ (n\)” style="text-align:left; ">4 | \ (m_ {n}\)” style="text-align:left; ">\(3.5666673798563\) | \ (\ delta_ {n}\)” style="text-align:left; ">\(4.6689537409802\) |
| \ (n\)” style="text-align:left; ">5 | \ (m_ {n}\)” style="text-align:left; ">\(3.5692435316371\) | \ (\ delta_ {n}\)” style="text-align:left; ">\(4.6691571813703\) |
| \ (n\)” style="text-align:left; ">6 | \ (m_ {n}\)” style="text-align:left; ">\(3.5697952937499\) | \ (\ delta_ {n}\)” style="text-align:left; ">\(4.6691910014915\) |
| \ (n\)” style="text-align:left; ">7 | \ (m_ {n}\)” style="text-align:left; ">\(3.5699134654223\) | \ (\ delta_ {n}\)” style="text-align:left; ">\(4.6691994819801\) |
| \ (n\)” style="text-align:left; ">8 | \ (m_ {n}\)” style="text-align:left; ">\(3.5699387742333\) | \ (\ delta_ {n}\)” style="text-align:left; ">\(4.6692010884670\) |
| \ (n\)” style="text-align:left; ">9 | \ (m_ {n}\)” style="text-align:left; ">\(3.5699441946081\) | \ (\ delta_ {n}\)” style="text-align:left; ">\(4.6692015881423\) |
| \ (n\)” style="text-align:left; ">10 | \ (m_ {n}\)” style="text-align:left; ">\(3.5699453554865\) | \ (\ delta_ {n}\)” style="text-align:left; ">\(4.6692023902759\) |
| \ (n\)” style="text-align:left; ">11 | \ (m_ {n}\)” style="text-align:left; ">\(3.5699456041111\) | \ (\ delta_ {n}\)” style="text-align:left; ">\(4.6691974782669\) |
| \ (n\)” style="text-align:left; ">12 | \ (m_ {n}\)” style="text-align:left; ">\(3.5699456573588\) | \ (\ delta_ {n}\)” style="text-align:left; ">\(4.6693329633696\) |
| \ (n\)” style="text-align:left; ">13 | \ (m_ {n}\)” style="text-align:left; ">\(3.5699456687629\) | \ (\ delta_ {n}\)” style="text-align:left; "> |
| \ (n\)” style="text-align:left; ">14 | \ (m_ {n}\)” style="text-align:left; ">\(3.5699456712052\) | \ (\ delta_ {n}\)” style="text-align:left; "> |
Cuadro 13.2: Los primeros catorce valores y estimaciones del delta de Feigenbaum.\(m_{n}\)
con valores iniciales\(x_{0}=1 / 2\) y el método de\(x_{0}^{\prime}=0 .\) Newton luego resuelve para\(m_{n}\) iterando
\[\mu^{(i+1)}=\mu^{(i)}-\frac{x_{N}-1 / 2}{x_{N}^{\prime}}, \nonumber \]
hasta la convergencia de\(\mu^{(i)}\) a\(m_{n}\). En doble precisión, hemos podido lograr una precisión de aproximadamente 14 dígitos, que encontramos que se puede obtener en menos de 5 iteraciones del método de Newton.
Para que el método de Newton converja\(m_{n}\), necesitamos una buena conjetura para\(\mu^{(0)} .\) Podemos usar la mejor estimación previa para el delta de Feigenbaum para predecir\(m_{n}\). De\((13.40)\), encontramos
\[\mu^{(0)}=m_{n-1}+\frac{m_{n-1}-m_{n-2}}{\delta_{n-2}} . \nonumber \]
Aunque no podemos computar\(\delta_{n-2}\) sin saber\(m_{n}\), podemos sin embargo usar la estimación\(\delta_{n-2} \approx \delta_{n-3} .\) El cómputo, entonces, comienza con\(n=2\), y podemos comenzar por tomar\(\delta_{-1}=4.4\), de manera que, por ejemplo,
\[\begin{aligned} \mu^{(0)} &=3.2361+\frac{3.2361-2}{4.4} \\ &=3.5170 . \end{aligned} \nonumber \]
Utilizando este algoritmo, hemos producido Tabla\(13.2\) para\(m_{n}\), con los cálculos correspondientes de\(\delta_{n} .\) A medida que los valores de\(m_{n}\) convergen, los valores correspondientes de\(\delta_{n}\) comienzan a perder precisión. Parecería que nuestra mejor estimación de la tabla es\(\delta \approx 4.66920\), en comparación con el valor conocido de\(\delta=4.669201609102990 \ldots\), calculada por un algoritmo diferente capaz de lograr una mayor precisión.
Extraño atractor del péndulo caótico
Después de la cascada de duplicación del período, el movimiento del péndulo se vuelve caótico. Elegimos valores de parámetros\(q=4, f=1.5\), y\(\omega=2 / 3\) en el régimen caótico, y después de descartar un transitorio inicial de 256 períodos de forzamiento, computamos una sección de Poincaré de la trayectoria fase-espacio en el\(\theta-\dot{\theta}\) plano, muestreando puntos cada período de forzamiento. Los valores de la variable periódica\(\theta\) se mapean en el intervalo\(-\pi<\theta<\pi\). La sección completa de Poincaré que consta de 50,000 puntos se muestra en el dibujo superior de la figura 13.11, y en el dibujo inferior se muestra una explosión de los puntos dentro del rectángulo dibujado (a partir de una muestra de 200,000 puntos sobre todo el atractor).
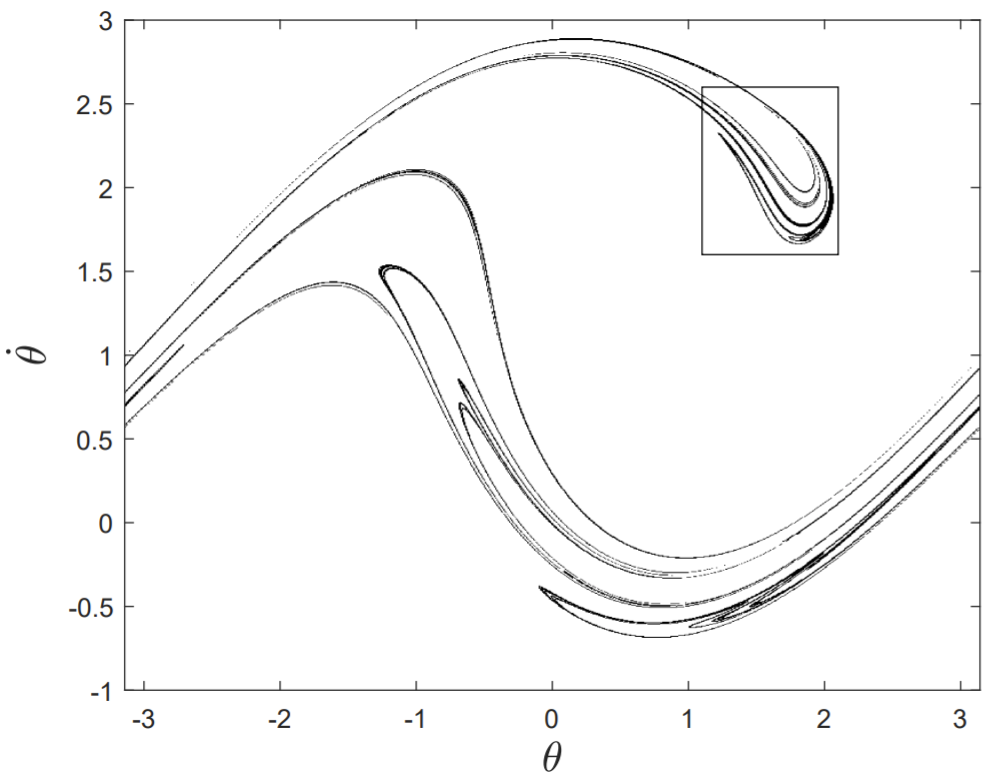
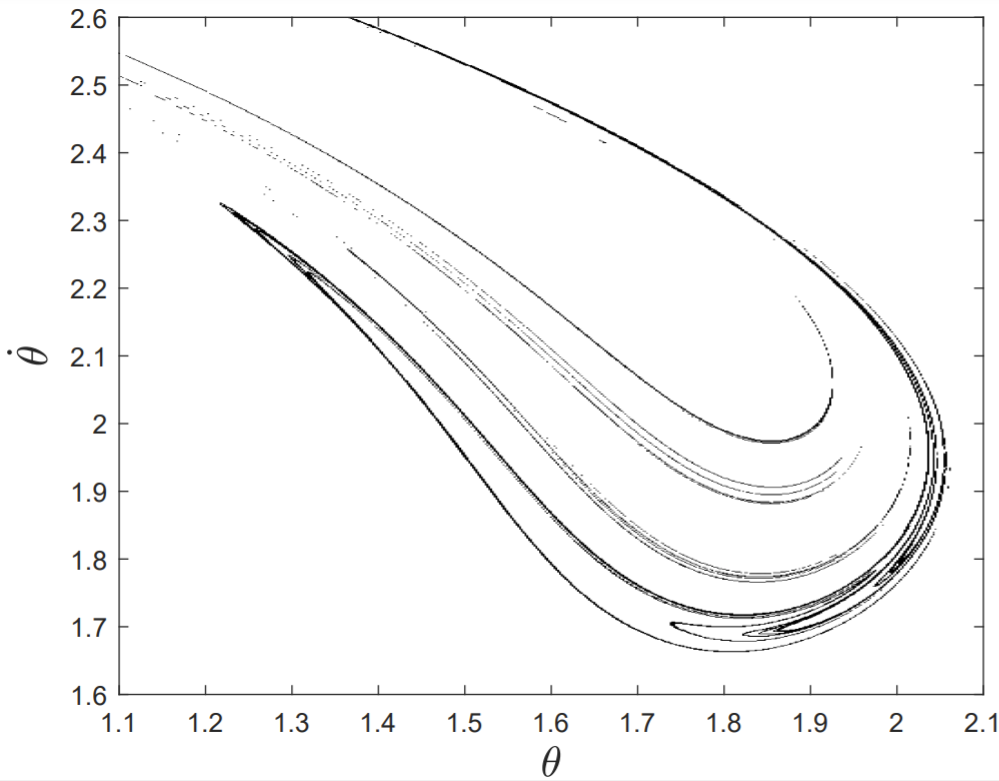
De la Fig. 13.11, se desprende que la sección de Poincaré tiene estructura en todas las escalas, lo que recuerda a los fractales clásicos discutidos en\(\S 12.7\). El conjunto de puntos mostrado en la Fig. 13.11 se denomina atractor extraño, y se verá que tiene una dimensión de correlación fraccionaria.
Utilizando el algoritmo para calcular una dimensión de correlación discutida en\(\S 12.7\), dibujamos un
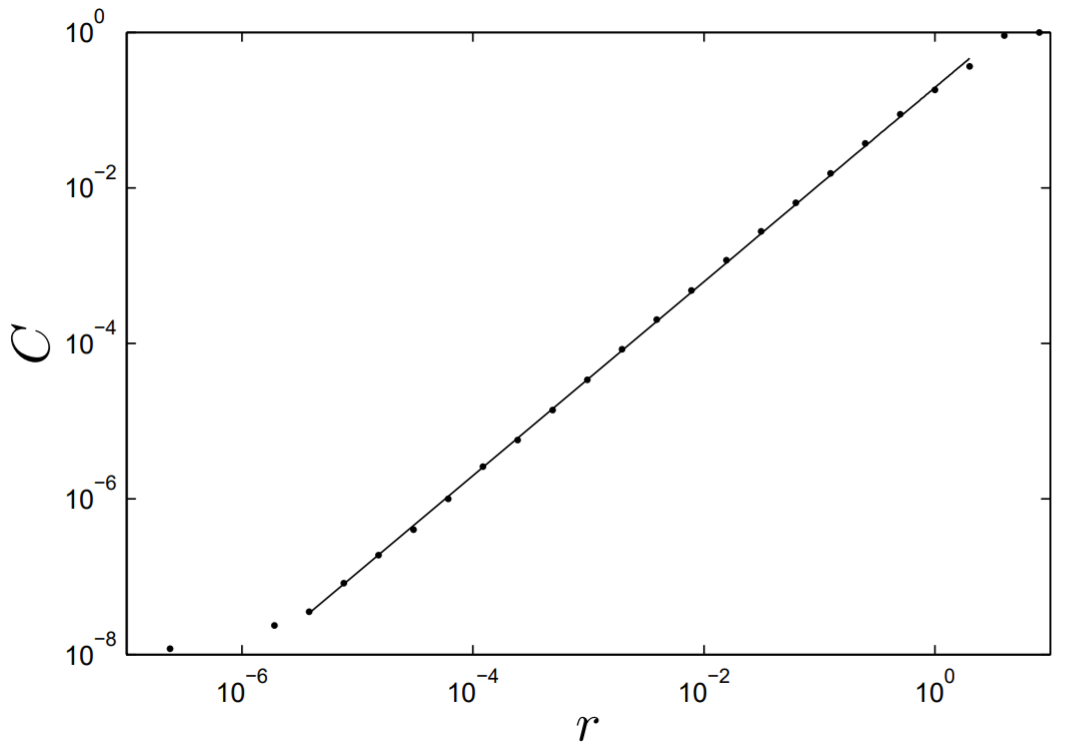
Gráfica log-log de la integral de correlación\(C(r)\) versus\(r\), mostrada en la Fig. 13.12. Un ajuste de mínimos cuadrados de una línea recta a la región media de la parcela produce una dimensión de correlación para la sección de Poincaré de aproximadamente\(D=1.25\).