5.4: Hacer operaciones matemáticas en matrices

Representar los lazos entre actores como matrices puede ayudarnos a ver patrones realizando manipulaciones simples como sumar vectores de fila o particionar la matriz en bloques. Los analistas de redes sociales utilizan una serie de otras operaciones matemáticas que se pueden realizar en matrices para una variedad de propósitos (suma y resta de matriz, transposición, inversión, multiplicación de matrices y algunas otras cosas más exóticas como determinantes y valores propios). Sin tratar de enseñarte álgebra matricial, es útil conocer al menos un poco sobre algunas de estas operaciones matemáticas, y para qué se utilizan en el análisis de redes sociales.

UCINET tiene funciones integradas para realizar la mayoría de las funciones de álgebra matricial Busque en el menú Herramientas>Álgebra de Matrices. Si conoces algún álgebra matricial, encontrarás que esta herramienta te permite hacer casi cualquier cosa para matricular datos que puedas desear. Pero, sí necesitas saber lo que estás haciendo. La pantalla de ayuda para este comando muestra cómo identificar la matriz o matrices que se van a manipular, y los algoritmos que se pueden aplicar.

Transposición de una matriz

Esto simplemente significa intercambiar las filas y columnas para que i se convierta en j, y viceversa. Si tomamos la transposición de una matriz de adyacencia dirigida y examinamos sus vectores de fila (¡ya deberías conocer toda esta jerga!) , estamos viendo las fuentes de vínculos dirigidos a un actor. El grado de similitud entre una matriz de adyacencia y la transposición de esa matriz es una forma de resumir el grado de simetría en el patrón de relaciones entre actores. Es decir, la correlación entre una matriz de adyacencia y la transposición de esa matriz es una medida del grado de reciprocidad de los lazos (piense un poco en esa afirmación). La reciprocidad de vínculos puede ser una propiedad muy importante de una estructura social porque se relaciona tanto con el equilibrio como con el grado y forma de jerarquía en una red. Este comando también está disponible como Data>Transpose.

Tomando la inversa de una matriz

Se trata de una operación matemática que encuentra una matriz que, cuando se multiplica por la matriz original, produce una nueva matriz con unos en la diagonal principal y ceros en otra parte (que se llama matriz de identidad). Sin entrar más en esto, se puede pensar en lo inverso de una matriz como algo así como el “opuesto” de la matriz original. Las inversiones matriciales se utilizan principalmente en el cálculo de otras cosas en el análisis de redes sociales. A veces son interesantes para estudiar en sí mismos, sin embargo. Es como mirar letras negras en papel blanco versus letras blancas en papel negro: a veces ves cosas diferentes. Los inversos se calculan con Herramientas>Álgebra Matriz.

Suma de matriz y resta de matriz

Estas son las operaciones matemáticas matriciales más fáciles. Uno simplemente suma o resta cada elemento i, j correspondiente de las dos (o más) matrices. Por supuesto, las matrices que esto se está haciendo para tener los mismos números de I y j elementos (esto se llama “conformable” a suma y resta) - y, los valores de i y j tienen que estar en el mismo orden en cada matriz.

La suma y resta de matriz se utilizan con mayor frecuencia en el análisis de redes cuando intentamos simplificar o reducir la complejidad del multiplex (se registran múltiples relaciones como matrices o rebanadas separadas) datos a formas más simples. Si tuviera una matriz simétrica que representara el empate “intercambia dinero” y otra que representara la relación “intercambios bienes” podría agregar las dos matrices para indicar la intensidad de la relación cambiaria. Los pares con una puntuación de cero no tendrían relación, aquellos con un “1" estarían involucrados en trueque o bolsa de materias primas, y aquellos con un “2" tendrían relaciones tanto de trueque como de intercambio de materias primas. Si restara la matriz de intercambio de “bienes” de la matriz de “cambio de dinero”, una puntuación de -1 indicaría pares con una relación de trueque; una puntuación de cero indicaría o bien ninguna relación o un empate de trueque y mercancía; una puntuación de +1 indicaría pares con solo una relación de intercambio mercantilizada. Para diferentes preguntas de investigación, cualquiera o ambos enfoques podrían ser útiles. Herramientas>Álgebra de Matrices son una forma de hacer este tipo de transformaciones de datos.

Multiplicación matricial y multiplicación matricial booleana

La multiplicación de matrices es una operación algo inusual, pero puede ser muy útil para el analista de redes. Aquí tendrás que ser un poco paciente. Primero necesitamos mostrarte cómo hacer multiplicación matricial y algunos resultados importantes (como lo que sucede cuando multiplicas una matriz de adyacencia por sí misma, o la elevas a una potencia). Entonces, trataremos de explicar por qué esto es útil.

Para multiplicar dos matrices, deben ser “conformables” a la multiplicación. Esto significa que el número de filas en la primera matriz debe ser igual al número de columnas en la segunda. Por lo general, el análisis de red utiliza matrices de adyacencia, que son cuadradas, y por lo tanto, conformables para la multiplicación. Multiplicar una matriz por sí misma (es decir, elevarla a una potencia) y multiplicar una matriz cuadrada por su transposición son obviamente “conformables”. A diferencia de la multiplicación regular de números individuales X*Y no es lo mismo que Y*X en la multiplicación matricial — ¡el orden importa!

Para multiplicar dos matrices, comience en la esquina superior izquierda de la primera matriz y multiplique cada celda de la primera fila de la primera matriz por los valores en cada celda de la primera columna de la segunda matriz, y sumar los resultados. Proceder por cada celda en cada fila de la primera matriz, multiplicando por la columna en la segunda. Para realizar una multiplicación matricial booleana, proceda de la misma manera, pero ingrese un cero en la celda si el producto de multiplicación es cero, y uno si no es cero. Un ejemplo ayuda. Supongamos que quisiéramos multiplicar las dos matrices en la figura 5.10.

0	1
2	3
4	5

tiempos

6	7	8
9	10	11

Figura 5.10. Dos matrices a multiplicar.

El resultado se muestra en la Figura 5.11.

(0*6) + (1*9)	(0*7) + (1*10)	(0*8) + (1*11)
(2*6) + (3*9)	(2*7) + (3*10)	(2*8) + (3*11)
(4*6) + (5*9)	(4*7) + (5*10)	(4*8) + (5*11)

Figura 5.11. Resultado de la multiplicación matricial.

La operación matemática en sí misma no nos interesa aquí (cualquier número de programas puede realizar multiplicación matricial). Pero, la operación es útil cuando se aplica a una matriz de adyacencia. Consideremos de nuevo a nuestros cuatro amigos, en la figura 5.12.

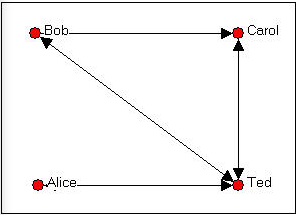
Figura 5.12. Gráfica dirigida de relaciones de amistad entre Bob, Carol, Ted y Alice

La matriz de adyacencia para los cuatro actores B, C, T y A (en ese orden) se muestra como Figura 5.13.

—	1	1	0
0	—	1	0
1	1	—	1
0	0	1	—

Figura 5.13. Matriz de adyacencia para gráfica en la Figura 5.12.

Otra forma de pensar sobre esta matriz es notar que nos dice si hay un camino de cada actor a cada actor. Un uno representa la presencia de un camino, un cero representa la falta de un camino. La matriz de adyacencia es exactamente lo que sugiere su nombre —nos dice qué actores son adyacentes, o tienen un camino directo de uno a otro.

Ahora supongamos que multiplicamos esta matriz de adyacencia por sí misma (es decir, elevamos la matriz a la 2da potencia, o la cuadramos). Trataremos a los “autolazos” como ceros, los cuales, efectivamente, los ignoran. El cálculo de la matriz al cuadrado se muestra como Figura 5.14.

(0*0) + (1*0) + (1*1) + (0*0)	(0*1) + (1*0) + (1*1) + (0*0)	(0*1) + (1*1) + (1*0) + (0*1)	(0*0) + (1*0) + (1*1) + (0*0)
(0*0) + (0*0) + (1*1) + (0*0)	(0*1) + (0*0) + (1*1) + (0*0)	(0*1) + (0*1) + (1*0) + (0*1)	(0*0) + (0*0) + (1*1) + (0*0)
(1*0) + (1*0) + (0*1) + (1*0)	(1*1) + (1*0) + (0*1) + (1*0)	(1*1) + (1*1) + (0*0) + (1*1)	(1*0) + (1*0) + (0*1) + (1*0)
(0*0) + (0*0) + (1*1) + (0*0)	(0*1) + (0*0) + (1*1) + (0*0)	(0*1) + (0*1) + (1*0) + (0*1)	(0*0) + (0*0) + (1*1) + (0*0)

es igual a:

1	1	1	1
1	1	0	1
0	1	3	0
1	1	0	1

Figura 5.14. Matriz de cuadratura 5.13.

Esta matriz (es decir, la matriz de adyacencia al cuadrado) cuenta el número de rutas entre dos nodos que son de longitud dos. Detente por un minuto y verifica esta afirmación (vuelve a la gráfica y encuentra los caminos). Por ejemplo, nótese que el actor “B” está conectado a cada uno de los otros actores por un camino de longitud dos; y que no hay más de uno de esos caminos hacia cualquier otro actor. El actor T está conectado consigo mismo por caminos de longitud dos, tres veces. Esto se debe a que el actor T tiene vínculos recíprocos con cada uno de los otros tres actores. No hay vía de longitud dos de T a B (aunque hay una vía de longitud uno).

Entonces, la matriz de adyacencia nos dice cuántos caminos de longitud hay uno de cada actor a otro actor. La matriz de adyacencia al cuadrado nos dice cuántos caminos de longitud dos hay de cada actor a uno a otro actor. Es cierto (pero no te lo mostraremos) que la matriz de adyacencia en cubos cuenta el número de caminos de longitud tres de cada actor a uno a otro actor. Y así sucesivamente...

Si calculamos el producto booleano, en lugar del producto de matriz simple, la matriz de adyacencia al cuadrado nos diría si había una ruta de longitud dos entre dos actores (no cuántos de esos caminos había). Si tomamos la matriz cuadrada booleana y la multiplicamos por la matriz de adyacencia usando multiplicación booleana, el resultado nos diría qué actores estaban conectados por una o más vías de longitud tres. Y así sucesivamente...

Ahora, finalmente: ¿por qué debería importarte?

Algunas de las propiedades más fundamentales de una red social tienen que ver con lo conectados que están los actores entre sí. Las redes que tienen pocas o débiles conexiones, o donde algunos actores están conectados solo por caminos de gran longitud pueden mostrar baja solidaridad, tendencia a desmoronarse, respuesta lenta a estímulos, y similares. Las redes que tienen conexiones cada vez más fuertes con caminos más cortos entre los actores pueden ser más robustas y más capaces de responder de manera rápida y efectiva. Medir el número y la longitud de las vías entre los actores de una red nos permite indexar estas tendencias importantes de redes enteras.

Las posiciones de los actores individuales en las redes también se describen de manera útil por el número y la longitud de los caminos que tienen hacia otros actores. Los actores que tienen muchos caminos hacia otros actores pueden ser más influyentes con respecto a ellos. Actores que tienen caminos cortos hacia más otros actores pueden mí figuras más influyentes o centrales. Entonces, el número y la longitud de las vías en una red son muy importantes para comprender tanto las limitaciones como las oportunidades del individuo, y para comprender el comportamiento y los potenciales de la red en su conjunto.

Hay muchas medidas de posición individual y estructura general de red que se basan en si hay vías de longitudes dadas entre actores, la longitud de el camino más corto entre dos actores y el número de vías entre actores. De hecho, la mayoría de las medidas básicas de redes, medidas de centralidad y poder, y medidas de agrupaciones y subestructuras de redes se basan en observar el número y la longitud de las vías entre los actores.

Para la mayoría de los análisis, no tendrá que manipular matrices: UCINET y otros programas ya han construido algoritmos que tienen el cómputo para hacer estas operaciones. Sin embargo, la mayor parte del trabajo computacional en el análisis de redes se realiza con matemáticas matriciales, por lo que para entender lo que está sucediendo, es útil comprender lo básico.