18.2: Describiendo una red

La mayoría de los científicos sociales tienen un conocimiento práctico razonable de estadísticas básicas univariadas y bivariadas descriptivas e inferenciales. Muchas de estas herramientas encuentran aplicación inmediata en el trabajo con datos de redes sociales. Sin embargo, hay dos características distintivas bastante importantes para aplicar estas herramientas a los datos de la red.

En primer lugar, y lo más importante, el análisis de redes sociales es sobre las relaciones entre actores, no sobre las relaciones entre variables. La mayoría de los científicos sociales han aprendido sus estadísticas con aplicaciones al estudio de la distribución de las puntuaciones de actores (casos) sobre variables, y las relaciones entre estas distribuciones. Aprendemos sobre la media de un conjunto de puntajes sobre la variable “ingreso”. Aprendemos sobre el coeficiente de correlación de momento de producto de orden cero de Pearson para indexar la asociación lineal entre la distribución de los ingresos del actor y el logro educativo del actor.

La aplicación de estadísticas a las redes sociales también se trata de describir distribuciones y relaciones entre distribuciones. Pero, más que describir distribuciones de atributos de actores (o “variables”), nos preocupa describir las distribuciones de relaciones entre actores. Al aplicar la estadística a los datos de la red, nos preocupan temas como la fuerza promedio de las relaciones entre actores; nos preocupan preguntas como “¿se correlaciona la fuerza de los lazos entre actores en una red con la centralidad de los actores en la red?” La mayoría de las herramientas estadísticas descriptivas son las mismas para el análisis de atributos y para el análisis relacional, ¡pero el tema es bastante diferente!

Segundo, muchas de las herramientas de la estadística inferencial estándar que aprendimos del estudio de las distribuciones de atributos no se aplican directamente a los datos de la red. La mayoría de las fórmulas estándar para calcular errores estándar estimados, calcular estadísticas de pruebas y evaluar la probabilidad de hipótesis nulas que aprendimos en las estadísticas básicas no funcionan con datos de red (y, si se usan, pueden darnos respuestas “falsas positivas” con más frecuencia que “falso negativo”). Esto se debe a que las “observaciones” o puntuaciones en los datos de la red no son muestreos “independientes” de las poblaciones. En el análisis de atributos, a menudo es muy razonable suponer que los ingresos de Fred y la educación de Fred son un “juicio” que es independiente de los ingresos de Sue y de la educación de Sue. Podemos tratar a Fred y Sue como réplicas independientes.

En el análisis de redes, nos enfocamos en las relaciones, no en los atributos. Entonces, una observación bien podría ser el vínculo de Fred con Sue; otra observación podría ser el empate de Fred con George; otra más podría ser el empate de Sue con George. Estas no son réplicas “independientes”. Fred está involucrado en dos observaciones (como lo son Sue an George), probablemente no sea razonable suponer que estas relaciones son “independientes” porque ambas involucran a George.

Las fórmulas estándar para calcular errores estándar y pruebas inferenciales sobre atributos generalmente asumen observaciones independientes. Aplicarlos cuando las observaciones no son independientes puede ser muy engañoso. En cambio, se utilizan enfoques numéricos alternativos para estimar errores estándar para las estadísticas de red. Estos enfoques de “boot-strapping” (y permutaciones) calculan distribuciones de muestreo de estadísticas directamente de las redes observadas mediante el uso de asignación aleatoria en cientos o miles de ensayos bajo el supuesto de que las hipótesis nulas son verdaderas.

Estos puntos generales serán más claros a medida que examinemos algunos casos reales. Entonces, comencemos con las estadísticas descriptivas e inferenciales univariadas más simples, para luego pasar a problemas algo más complicados.

Estadística Descriptiva Univariada

Para la mayoría de los ejemplos de este capítulo, volveremos a enfocarnos en el conjunto de datos Knoke que describe las dos relaciones del intercambio de información y el intercambio de dinero entre diez organizaciones que operan en el ámbito del bienestar social. En la Figura 18.1 se enumeran estos datos.

Figura 18.1: Listado (Datos>Display) de matrices de información y cambio de dinero de Knoke

Estos datos particulares resultan ser asimétricos y binarios. La mayoría de las herramientas estadísticas para trabajar con datos de red se pueden aplicar a datos simétricos, y datos donde se valoran las relaciones (fuerza, costo, probabilidad de empate). Al igual que con cualquier estadística descriptiva, la escala de medición (binaria o valorada) sí importa en la toma de decisiones adecuadas sobre la interpretación y aplicación de muchas herramientas estadísticas.

Los datos que se analizan con herramientas estadísticas cuando estamos trabajando con datos de red son las observaciones sobre las relaciones entre actores. Entonces, en cada matriz, tenemos 10 x 10 = 100 observaciones o casos. Para muchos análisis, los lazos de los actores consigo mismos (la diagonal principal) no son significativos, y no se utilizan, por lo que habría\(\left( N * N - 1 = 90 \right)\) observations. If data are symmetric (i.e. \(X_{ij} = X_{ji}\)), half of these are redundant, and wouldn't be used, so there would be \(\left( N * N - 1 / 2 = 45 \right)\) observations.

Lo que nos gustaría resumir con nuestra estadística descriptiva son algunas características de la distribución de estos puntajes. Herramientas>Estadísticas Univariables se puede utilizar para generar las medidas más utilizadas para cada matriz (seleccione la matriz en el cuadro de diálogo y elija si desea o no incluir la diagonal). La Figura 18.2 muestra los resultados de nuestros datos de ejemplo, excluyendo la diagonal.

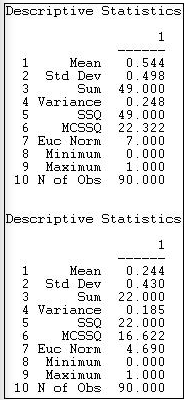
Figura 18.2: Estadísticas descriptivas univariadas para redes de información Knoke y dinero entero

Para la relación de intercambio de información, vemos que tenemos 90 observaciones que van desde una puntuación mínima de cero hasta una máxima de una. La suma de los lazos es 49, y el valor promedio de los lazos es 49/90 = .544. Dado que la relación ha sido codificada como una variable “ficticia” (cero para ninguna relación, una para una relación) la media es también la proporción de posibles vínculos que están presentes (o la densidad), o la probabilidad de que algún empate dado entre dos actores aleatorios esté presente (54.4% de probabilidad).

También se dan varias medidas de la variabilidad de la distribución. Se calculan las sumas de las desviaciones cuadradas de la media, varianza y desviación estándar, pero son más significativas para los datos valorados que los binarios. También se proporciona la norma euclidiana (que es la raíz cuadrada de la suma de valores cuadrados). Una medida no dada, pero a veces útil es el coeficiente de variación (desviación estándar/media por 100) es igual a 91.5. Esto sugiere bastante variación como porcentaje de la puntuación promedio. La UCINET no proporciona estadísticas sobre la forma distribucional (sesgo o curtosis).

Un escaneo rápido nos dice que la media (o densidad) para el intercambio de dinero es menor, y tiene una variabilidad ligeramente menor.

Además de examinar toda la distribución de los vínculos, podríamos querer examinar la distribución de los vínculos para cada actor. Dado que la relación que estamos viendo es asimétrica o dirigida, es posible que queramos resumir aún más el envío (fila) y la recepción (columna) de cada actor. Las figuras 18.3 y 18.4 muestran los resultados de Herramientas>Estadísticas Univariables para filas (envío de empate) y columnas (recepción de empate) de la matriz de relación de información.

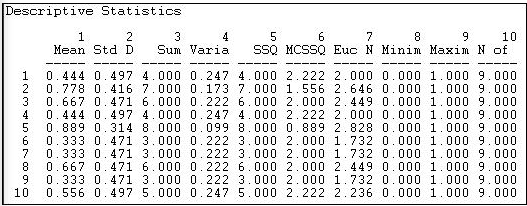
Figura 18.3: Estadísticas descriptivas univariadas para filas de la red de información Knoke

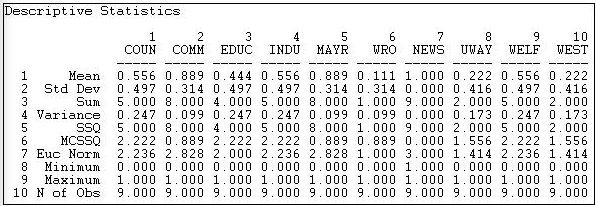
Figura 18.4: Estadísticas descriptivas univariadas para columnas de la red de información Knoke

Vemos que el actor 1 (COUN) tiene una media (o densidad) de envío de empate de 0.444. Es decir, este actor envió cuatro vínculos a los otros nueve actores disponibles. El actor 1 recibió algo más información de la que envió, ya que su media de columna es .556. Al escanear hacia abajo la columna (en la figura 18.3) o fila (en la figura 18.4) de medias, observamos que hay bastante variabilidad entre actores —algunos envían más y obtienen más información que otros.

Con datos valorados, las medias produjeron indexar la fuerza promedio de los lazos, más que la probabilidad de vínculos. Con datos valorados, las medidas de variabilidad pueden ser más informativas que con datos binarios (ya que la variabilidad de una variable binaria es estrictamente una función de su media).

El punto principal de esta breve sección es que cuando usamos estadísticas para describir datos de red, estamos describiendo propiedades de la distribución de relaciones, o vínculos entre actores, en lugar de propiedades de la distribución de atributos entre actores. Las ideas básicas de tendencia central y dispersión de distribuciones se aplican a las distribuciones de vínculos relacionales exactamente de la misma manera que lo hacen para atribuir variables —pero estamos describiendo relaciones, no atributos.

Hipótesis sobre una media o densidad

De las diversas propiedades de la distribución de una sola variable (por ejemplo, tendencia central, dispersión, asimetría), usualmente estamos más interesados en la tendencia central.

Si estamos trabajando con la distribución de las relaciones entre actores en una red, y nuestra medida de fuerza de unión es binaria (cero/uno), la tendencia media o central es también la proporción de todos los lazos que están presentes, y es la “densidad”.

Si estamos trabajando con la distribución de las relaciones entre actores en una red, y se valora nuestra medida de fuerza de vínculo, la tendencia central suele ser indicada por la fuerza media del empate en todas las relaciones.

Es posible que queramos probar hipótesis sobre la densidad o la fuerza media del lazo de una red. En el análisis de variables, se está probando una hipótesis sobre una media o proporción de una sola muestra. Podríamos querer estar seguros de que realmente hay lazos presentes (hipótesis nula: la densidad de la red es realmente cero, y cualquier desviación que observemos se debe a una variación aleatoria). Podríamos querer probar la hipótesis de que la proporción de vínculos binarios presentes difiere de 0.50; podríamos querer probar la hipótesis de que la fuerza promedio de un empate valorado difiere de “3”.

Redes>Comparar densidades>Contra parámetro teórico realiza una prueba estadística para comparar el valor de una densidad o fuerza de amarre promedio observada en una red con un valor de prueba.

Supongamos que pienso que todas las organizaciones tienen tendencia a querer distribuir directamente información a todas las demás en su campo como una forma de legitimar ellos mismos. Si esta teoría es correcta, entonces la densidad de la red de información de Knoke debería ser 1.0. Podemos ver que esto no es cierto. Pero, quizás la diferencia entre lo que vemos (densidad = 0.544) y lo que predice la teoría (densidad = 1.000) se deba a la variación aleatoria (quizás cuando recogimos la información).

El cuadro de diálogo de la figura 18.5 configura el problema.

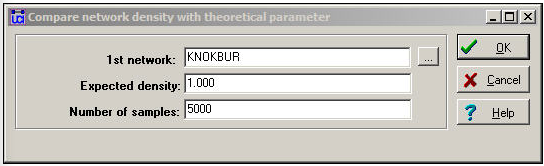
Figura 18.5: Diálogo de Densidades de comparación>Contra parámetro teórico

La “Densidad esperada” es el valor contra el que queremos probar. Aquí, estamos pidiendo los datos para convencernos de que podemos tener confianza en rechazar la idea de que las organizaciones envíen información a todas las demás en sus campos.

El parámetro “Número de muestras” se utiliza para estimar el error estándar para la prueba mediante “bootstrapping” o calculando la varianza de muestreo estimada del extraer 5000 submuestras aleatorias de nuestra red y construir una distribución de muestreo de medidas de densidad. La distribución muestral de un estadístico es la distribución de los valores de ese estadístico en muestreo repetido. La desviación estándar de la distribución muestral de un estadístico (cuánta variación esperaríamos ver de muestra a muestra solo por casualidad aleatoria) se denomina error estándar. La Figura 18.6 muestra los resultados de la prueba de hipótesis

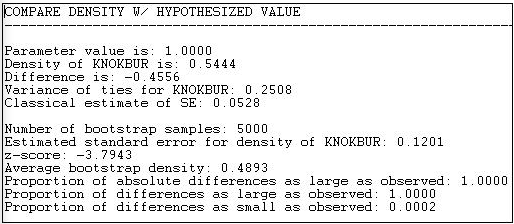
Figura 18.6: Resultados de las pruebas

Vemos que nuestro valor de prueba fue 1.000, el valor observado fue 0.5444, por lo que la diferencia entre los valores nulos y observados es -0.4556. ¿Con qué frecuencia ocurriría una diferencia tan grande por variación de muestreo aleatorio, si la hipótesis nula (densidad = 1.000) fuera realmente cierta en la población?

Usando la fórmula clásica para el error estándar de una media\(\left( s / \sqrt{N} \right)\) we obtain a sampling variability estimate of 0.0528. If we used this for our test, the test statistic would be -0.4556/0.0528 = 8.6 which would be highly significant as a t-test with N-1 degrees of freedom.

Sin embargo, si usamos el método bootstrap de construir 5000 redes mediante el muestreo de subconjuntos aleatorios de nodos cada vez, y calculando la densidad cada vez, la media de esta distribución de muestreo resulta ser 0.4893, y su desviación estándar (o el error estándar) resulta ser 0.1201.

Utilizando este error estándar alternativo basado en sorteos aleatorios de la muestra observada, nuestro estadístico de prueba es -3.7943. Esta prueba también es significativa (p = 0.0002).

¿Por qué hacer esto? La fórmula clásica da una estimación del error estándar (0.0528) que es mucho menor que la creada por el método bootstrap (0.1201). Esto se debe a que la fórmula estándar se basa en la noción de que todas las observaciones (es decir, todas las relaciones) son independientes. Pero, dado que los lazos son realmente generados por los mismos 10 actores, esto no es una suposición razonable. El uso de los datos reales sobre los actores reales —con las diferencias observadas en las medias y varianzas de los actores, es una aproximación mucho más realista a la variabilidad real del muestreo que ocurriría si, digamos, pasáramos de menos a Fred cuando recabamos los datos el martes.

En general, las fórmulas inferenciales estándar para calcular la variabilidad de muestreo esperada (es decir, errores estándar) dan valores poco realistas para los datos de la red. Utilizarlos da como resultado el peor tipo de error inferencial: el falso positivo, o rechazar el nulo cuando no deberíamos.