15.2: Terminologías de la Teoría Gráfica

Antes de pasar al modelado dinámico de redes reales, necesitamos cubrir algunos conceptos básicos de la teoría de grafos, especialmente las definiciones de términos técnicos utilizados en este campo. Comencemos con algo que ya hemos comentado anteriormente:

Una red (o gráfica) consiste en un conjunto de nodos (o vértices, actores) y un conjunto de aristas (o enlaces, lazos) que conectan esos nodos.

Como se indicó anteriormente, diferentes disciplinas utilizan diferentes terminologías para hablar de redes; los matemáticos usan “gráfico/vértex/borde”, los físicos usan “red/node/borde”, los informáticos usan “red/nodo/enlace”, los científicos sociales usan “red/actor/empate”, etc. Este es un problema típico cuando trabajas en una área de investigación interdisciplinaria como la ciencia de redes. Sólo tenemos que acostumbrarnos a ello. En este libro de texto, uso principalmente “red/nodo/borde” o “red/nodo/enlace”, pero a veces también puedo usar otros términos indistintamente.

Por cierto, algunas personas se preguntan cuáles son las diferencias entre una “red” y una “gráfica”. Yo diría que una “red” implica que es un modelo de algo real, mientras que una “gráfica” enfatiza más en los aspectos como objeto matemático abstracto (que también puede ser utilizado como modelo de algo real, claro). Pero esta distinción tampoco es tan esencial.

Para representar una red, necesitamos especificar sus nodos y bordes. Un término útil es vecino, definido de la siguiente manera:

Nodo\(j\) se llama vecino de nodo\(i\) si (y sólo si) nodo\(i\) está conectado al nodo\(j\).

La idea de vecinos es particularmente útil cuando intentamos relacionar modelos de red con modelos más clásicos como CA (donde las estructuras vecinales se asumieron regulares y homogéneas). Usando este término, podemos decir que el objetivo de la representación de la red es representar las relaciones de vecindad entre los nodos. Hay muchas formas diferentes de representar las redes, pero las siguientes dos son las más comunes:

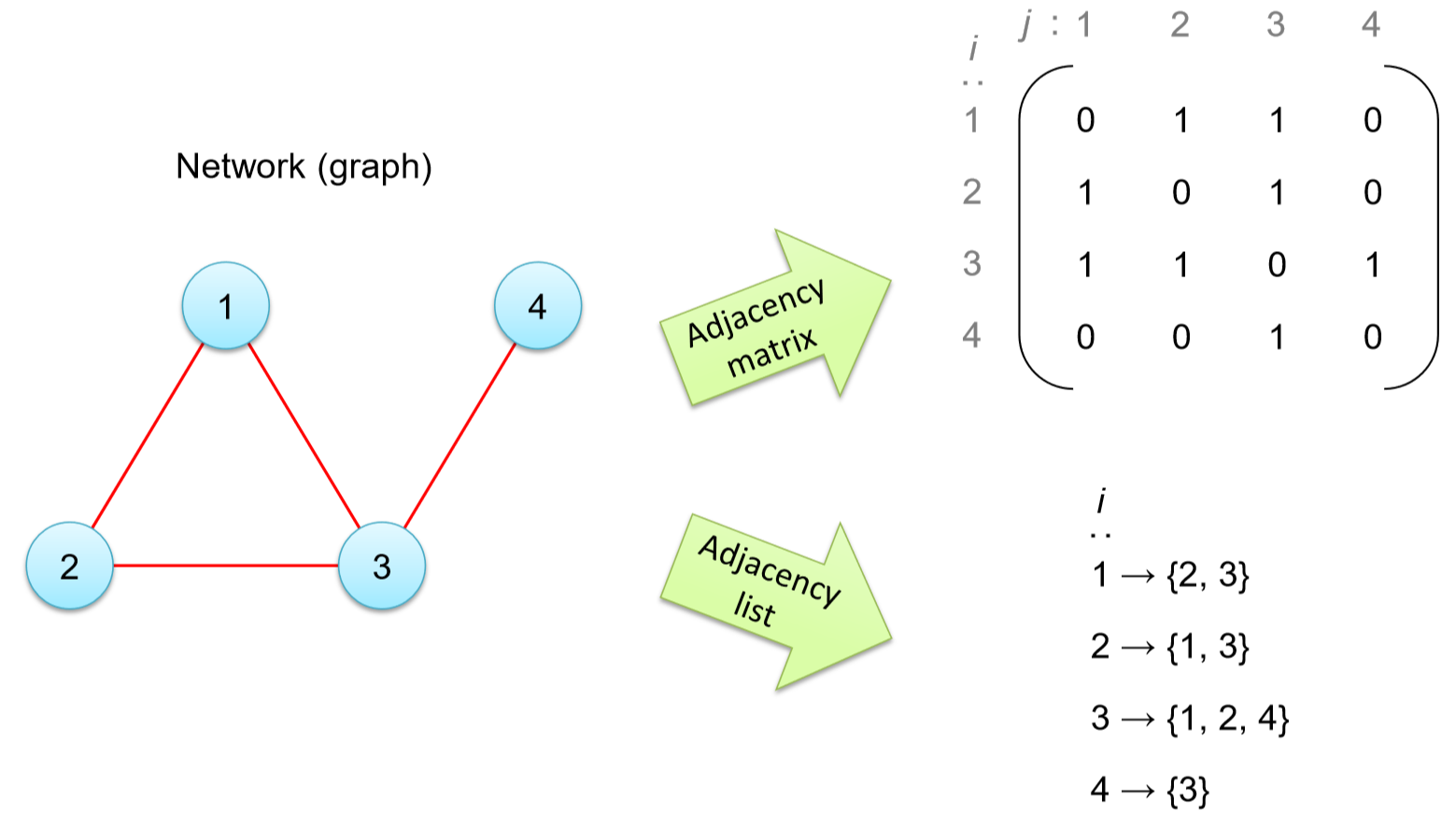
Matriz de adyacencia Una matriz con filas y columnas etiquetadas por nodos, cuyo componente\(i\) -ésima fila,\(j\) -ésima columna\(a_{ij}\) es 1 si el nodo\(i \) es vecino del nodo\(j\), o 0 en caso contrario.

Lista de adyacencia Una lista de listas de nodos cuyo\(i\) -ésimo componente es la lista de vecinos\(i\) del nodo.

La Figura 15.1 muestra un ejemplo de la matriz/lista de adyacencia. Como puede ver, la lista de adyacencia ofrece una representación más compacta y eficiente en memoria, especialmente si la red es escasa (es decir, si la densidad de red es baja, lo que suele ser el caso de la mayoría de las redes del mundo real). Mientras tanto, la matriz de adyacencia también tiene algunos beneficios, como su factibilidad para el análisis matemático y la facilidad de tener acceso a sus componentes específicos.

Aquí hay algunas terminologías más básicas:

Grado El número de aristas conectadas a un nodo. \(i\)El grado de Nodo a menudo se escribe como\(deg(i)\).

Figura\(\PageIndex{1}\): Ejemplos de una matriz adyacente y una lista adyacente.

• Caminar Una lista de bordes que están conectados secuencialmente para formar una ruta continua en una red. En particular:
• Sendero Un paseo que no pasa por ningún borde más de una vez.
• Sendero Un paseo que no pasa por ningún nodo (y por lo tanto cualquier borde, también) más de una vez.
• Ciclo Una caminata que inicia y termina en el mismo nodo sin pasar por ningún nodo más de una vez en su camino.
• Subgrafía Parte de la gráfica.
• Gráfico conectado Gráfico en el que existe una ruta entre cualquier par de nodos.
• Componente conectado Un subgrafo de una gráfica que está conectada dentro de sí misma pero no conectada al resto de la gráfica.

Ejercicio\(\PageIndex{1}\)

Consulte la siguiente red y responda las siguientes preguntas:

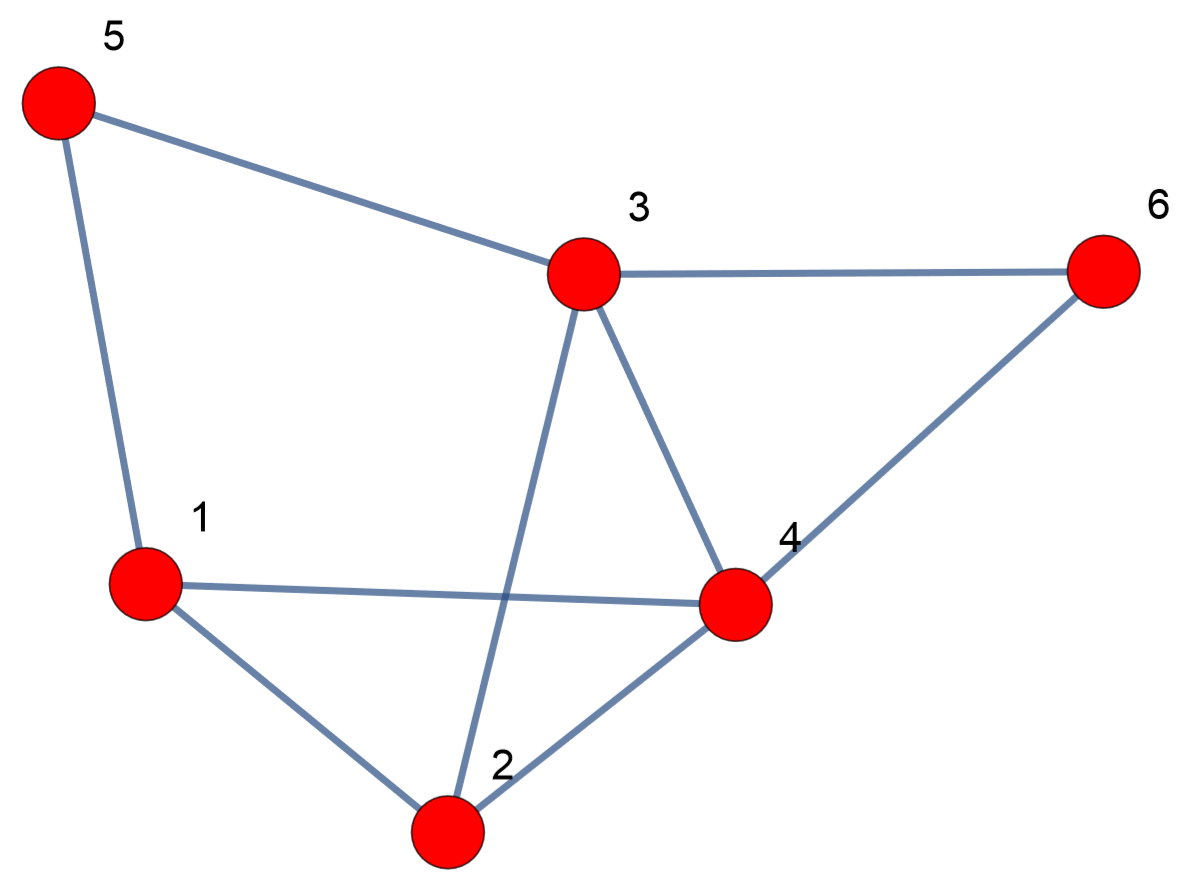
1. Representar la red en (a) una matriz de adyacencia y (b) una lista de adyacencias.

2. Determinar el grado para cada nodo.

3. Clasifique las siguientes caminatas como sendero, sendero, ciclo u otro.

• 6 → 3 → 2 → 4 → 2 → 1
• 1 → 4 → 6 → 3 → 2
• 5 → 1 → 2 → 3 → 5

4. Identificar todos los subgráficos de tres nodos completamente conectados (es decir, triángulos).

5. Retire los nodos 3 y 4 (y todos los bordes conectados a ellos). Luego identifique los componentes conectados en la gráfica resultante.

Algunas gráficas con propiedades topológicas características reciben sus propios nombres únicos, de la siguiente manera

• Gráfica completa Una gráfica en la que se conecta cualquier par de nodos (Fig. 15.2.2A).
• Gráfica regular Una gráfica en la que todos los nodos tienen el mismo grado (Fig.15.2.2B) .Cada gráfica completa es regular.
• Gráfica bipartita (\(n\)-partita) Una gráfica cuyos nodos se pueden dividir en dos (o\(n\)) grupos para que ningún borde conecte nodos dentro de cada grupo (Fig. 15.2.2C).
• Gráfica de árbol Gráfica en la que no hay ciclo (Fig. 15.2.2D). Una gráfica hecha de múltiples árboles se llama una gráfica de bosque. Cada gráfica de árbol o bosque es bipartita.
• Gráfica plana Gráfica que se puede dibujar gráficamente en un plano bidimensional sin cruces de borde (Fig. 15.2.2E). Cada gráfica de árbol o bosque es plana.

Figura\(\PageIndex{2}\): Ejemplos de gráficas con nombres específicos. A: Gráficas completas. B:Gráficas regulares. C: Gráficas bipartitas (los colores muestran grupos). D: Gráficas de árboles. E: Gráficas planas.

Ejercicio\(\PageIndex{2}\)

Calcula lo siguiente:

• El número de aristas en una gráfica completa hecha de\(n\) nodos
• El número de aristas en una gráfica regular hecha de\(n\) nodos cada uno de los cuales tiene grado\(k\)

Ejercicio\(\PageIndex{3}\)

Determine si las siguientes gráficas son planas o no:

• Una gráfica completa compuesta por cuatro nodos
• Una gráfica completa compuesta por cinco nodos
• Un gráfico bipartito hecho de un grupo de dos nodos y un grupo de tres nodos en el que están presentes todos los bordes entre grupos posibles
• Un gráfico bipartito formado por dos grupos de tres nodos en los que están presentes todos los bordes intergrupales posibles

Ejercicio\(\PageIndex{4}\)

Cada gráfico de árbol conectado hecho de\(n\) nodos tiene exactamente\(n − 1\) bordes. Explique por qué.

También hay clasificaciones de gráficas según los tipos de sus aristas:

• Borde no dirigido Una conexión simétrica entre nodos. Si el nodo\(i\) está conectado al nodo\(j\) por un borde no dirigido, entonces el nodo\(j\) también reconoce el nodo\(i\) como su vecino. Un gráfico hecho de bordes no dirigidos se llama gráfico no dirigido. La matriz de adyacencia de una gráfica no dirigida es siempre simétrica.
• Borde dirigido Una conexión asimétrica de un nodo a otro. Incluso si el nodo\(i\) está conectado al nodo\(j\) por un borde dirigido, la conexión no es necesariamente recíproca de nodo\(j\) a nodo\(i\). Un gráfico hecho de bordes dirigidos se llama gráfico dirigido. La matriz de adyacencia de una gráfica dirigida es generalmente asimétrica.
• Borde no ponderado Una arista sin ningún valor de peso asociado a ella. Solo hay dos posibilidades entre un par de nodos en una red con bordes no ponderados; si hay un borde entre ellos o no. La matriz de adyacencia de una red de este tipo está hecha de solo 0's y 1's.
• Borde ponderado Un borde con un valor de peso asociado a ella. Un peso generalmente viene dado por un número real no negativo, que puede representar una fuerza de conexión o distancia entre nodos, dependiendo de la naturaleza del sistema que se modele. La definición de la matriz de adyacencia se puede extender para contener esos valores de peso de borde para redes con bordes ponderados. La suma de los pesos de los bordes conectados a un nodo a menudo se llama la fuerza del nodo, que corresponde a un grado de nodo para las gráficas no ponderadas.
• Múltiples aristas Bordes que comparten el mismo origen y destino. Tales múltiples bordes conectan dos nodos más de una vez.
• Autobucle Un borde que se origina y termina en el mismo nodo.
• Gráfica simple Gráfica que no contiene bordes dirigidos, ponderados o múltiples, ni autobucles. La teoría gráfica tradicional se centra principalmente en gráficas simples.
• Multígrafo Una gráfica que puede contener múltiples aristas. Muchos matemáticos también permiten que los multígrafos contengan auto-bucles. Los multígrafos pueden ser no dirigidos o dirigidos.
• Hyperedge Un concepto generalizado de un borde que puede conectar cualquier número de nodos a la vez, no solo dos. Una gráfica hecha de hiperbordes se llama hipergrafía (no cubierta en este libro de texto).

De acuerdo con estas taxonomías, todos los ejemplos mostrados en la Fig. 15.2.2 son gráficas simples. Pero muchas redes del mundo real pueden y deben modelarse usando bordes dirigidos, ponderados y/o múltiples

Ejercicio\(\PageIndex{5}\)

Discutir qué tipo de gráfico se debe utilizar para modelar cada una de las siguientes redes. Asegúrese de considerar (a) la directedness edge, (b) la presencia de pesos de borde, (c) la posibilidad de múltiples bordes/auto-bucles, (d) posibilidad de conexiones entre tres o más nodos, y así sucesivamente.

• Árboles familiares/genealogías
• Telas alimenticias entre especies
• Caminos e intersecciones
• Páginas web y enlaces entre ellas
• Amistades entre las personas
• Matriculos/relaciones sexuales
• Solicitudes universitarias presentadas por estudiantes de secundaria
• Intercambios de correo electrónico entre compañeros de trabajo
• Redes sociales (Facebook, Twitter, Instagram, etc.)