3: Comportamiento Cerca de Trayectorias y Conjuntos Invariantes - Estabilidad
- Page ID
- 113628
Considere el campo vectorial general no autónomo en n dimensiones:
\[\dot{x} = f(x, t), x \in \mathbb{R}^n, \label{3.1}\]
y dejar\(\bar{x}(t, t_{0}, x_{0})\) ser una solución de este campo vectorial.
Muchas preguntas en las ODE se refieren a comprender el comportamiento de las soluciones vecinas cerca de una solución determinada y elegida. Desarrollaremos el marco general para considerar tales preguntas transformando la Ecuación\ ref {3.1} a una forma que nos permita considerar explícitamente estos temas.
Consideramos la siguiente transformación (dependiente del tiempo) de variables:
\[x = y+\bar{x}(t, t_{0}, x_{0}). \label{3.2}\]
Deseamos expresar la Ecuación\ ref {3.1} en términos de las variables y. Es importante entender lo que esto significará en términos de la Ecuación\ ref {3.2}. Para y pequeños significa que x está cerca de la solución de interés,\(\bar{x}(t, t_{0}, x_{0})\). En otras palabras, expresar el campo vectorial en términos de y nos proporcionará una forma explícita del campo vectorial para estudiar el comportamiento cercano\(\bar{x}(t, t_{0}, x_{0})\). Hacia este fin, comenzamos transformando la Ecuación\ ref {3.1} usando la Ecuación\ ref {3.2} de la siguiente manera:
\[\dot{x} = \dot{y}+ \dot{\bar{x}} = f(x, t) = f(y+\bar{x}, t), \label{3.3}\]
o
\(\dot{y} = f(y+\bar{x}, t)-\dot{\bar{x}}\),
\[= f(y+\bar{x}, t)-f(\bar{x}, t) \equiv g(y, t), g(0, t) = 0. \label{3.4}\]
De ahí que hayamos demostrado que las soluciones de la Ecuación\ ref {3.1} near\(\bar{x}(t, t_{0}, x_{0})\) son equivalentes a soluciones de la Ecuación\ ref {3.4} near y = 0.
La primera pregunta que queremos hacer relacionada con el comportamiento cercano\(\bar{x}(t, t_{0}, x_{0})\) es si esta solución es estable o no? Sin embargo, primero necesitamos definir matemáticamente lo que se entiende por este término “estable”. Ahora debemos saber que, sin pérdida de generalidad, podemos discutir esta cuestión en términos de la solución cero de la Ecuación\ ref {3.4}.
Comenzamos definiendo la noción de “estabilidad de Lyapunov” (o simplemente “estabilidad”).
Definición 13 (ESTABILIDAD LYAPUNOV)
y = 0 se dice que es Lyapunov estable en\(t_{0}\) si dado\(\epsilon > 0\) existe\(\delta = \delta (t_{0}, \epsilon)\) tal que
\[|y(t_{0})|<\delta \Rightarrow |y(t)|<\epsilon, \forall t>t_{0} \label{3.5}\]
Si una solución no es estable Lyapunov, entonces se dice que es inestable.
Definición 14 (INESTABLE)
Si y = 0 no es Lyapunov estable, entonces se dice que es inestable.
Entonces tenemos la noción de estabilidad asintótica.
Definición 15 (ESTABILIDAD ASIMPTÓTICA)
y = 0 se dice que es asintóticamente estable en\(t_{0}\) si:
- es Lyapunov estable en\(t_{0}\),
- existe\(\delta = \delta(t_{0}) > 0\) tal que:
\[|y(t_{0})| < \delta \Rightarrow lim_{t \rightarrow \infty} |y(t)| = 0 \label{3.6}\]
Tenemos varios comentarios sobre estas Definiciones.
- En términos generales, una solución estable de Lyapunov significa que si comienzas cerca de esa solución, te quedas cerca, para siempre. La estabilidad asintótica no solo significa que empiezas cerca y te quedas cerca para siempre, sino que en realidad te acercas “cada vez más” a la solución.
- La estabilidad es un concepto de tiempo infinito.
- Si la ODE es autónoma, entonces la cantidad se\(\delta = \delta(t_{0}, \epsilon)\) puede elegir para que sea independiente de\(t_{0}\).
- Las Definiciones de estabilidad no nos dicen cómo probar que una solución es estable (o inestable). Aprenderemos dos técnicas para analizar esta pregunta: la linealización y el método de Lyapunov (segundo).
- ¿Por qué se incluye la estabilidad de Lyapunov en la Definición de estabilidad asintótica? Porque es posible construir ejemplos donde las soluciones cercanas sí se acercan cada vez más a la solución dada como\(t \rightarrow \infty\), pero en el proceso hay intervalos intermedios de tiempo donde las soluciones cercanas hacen “grandes excursiones” lejos de la solución dada.
“Estabilidad” es una noción que se aplica a un “barrio” de una trayectoria. En este punto queremos formalizar diversas nociones relacionadas con la distancia y barrios en el espacio de fase. Por simplicidad en la expresión de estas ideas tomaremos como nuestro espacio de fase Rn. Los puntos en este espacio de fase se denotan\(x \in \mathbb{R}^n\),\(x \equiv (x_{1}, ..., x_{n})\). La norma, o longitud, de x, denotada |x| se define como:
\[|x| = \sqrt{x_{1}^{2}+x_{2}^{2}+ \cdots + x_{n}^{2}} = \sqrt{\sum_{i=1}^{n} x_{i}^{2}}.\]
La distancia entre dos puntos en\(x, y \in \mathbb{R}^n\) se define como:
\[ d(x,y) \equiv |x-y| = \sqrt{(x_{1}-y_{1})^2 + \cdots + (x_{n}-y_{n})^2} \]
\[= \sqrt{\sum_{i=1}^{n} \sqrt{(x_{i}-y_{i})^2}. \label{3.7}\]
La distancia entre puntos en\(\mathbb{R}^n\) debería ser algo familiar, pero ahora introducimos un nuevo concepto, la distancia entre un punto y un conjunto. Considera un conjunto M,\(M \subset \mathbb{R}^n\), vamos\(p \in \mathbb{R}^n\). Entonces la distancia de p a M se define de la siguiente manera:
\[dist(p, M) \equiv inf_{x \in M}|p-x|. \label{3.8}\]
Observamos que de la Definición se deduce que si\(p \in M\), entonces dist (p, M) = 0.
Anteriormente hemos definido la noción de un conjunto invariante. En términos generales, los conjuntos invariantes están compuestos por trayectorias. Ahora tenemos los antecedentes para discutir la noción de. Recordemos, que la noción de conjunto invariante solo se desarrolló para campos vectoriales autónomos. Entonces consideramos un campo vectorial autónomo:
\[\dot{x} = f(x), x \in \mathbb{R}^n, \label{3.9}\]
y denotan el flujo generado por este campo vectorial por\(\phi_{t}(\cdot)\). Deje que M sea un conjunto cerrado invariante (en muchas aplicaciones también podemos requerir que M esté acotado) y dejar que U M denota un vecindario de M.
La definición de estabilidad de Lyapunov de un conjunto invariante es la siguiente.
DEFINICIÓN 16 (ESTABILIDAD DE LYAPONOV
Se dice que M es Lyapunov estable si por algún barrio\(U \supset M, x \in U \Rightarrow \phi_{t}(x) \in U, \forall t > 0\).
De igual manera, tenemos la siguiente definición de estabilidad asintótica de un conjunto invariante.
DEFINICIÓN 17 (ESTABILIDAD ASIMPTÓTICA DE M)
Se dice que M es asintóticamente estable si
- es Lyapunov estable,
- existe un barrio\(U \supset M\) tal que\(\forall x \in U, dist((\phi_{t}x), M) \rightarrow 0\) como\(t \rightarrow \infty\).
En el enfoque de sistemas dinámicos para las ecuaciones diferenciales ordinarias se suele utilizar alguna terminología alternativa.
DEFINICIÓN 18
Si M es asintóticamente estable se dice que es un conjunto atrayente.
La importancia de atraer conjuntos es que son las regiones “observables” en el espacio de fases ya que son regiones a las que evolucionan trayectorias en el tiempo. El conjunto de puntos que evolucionan hacia un conjunto atrayente específico se conoce como la cuenca de atracción para ese conjunto invariante.
Definición 19 (CUENCA DE ATRACCIÓN
Vamos a\(B \subset \mathbb{R}^n\) denotar el conjunto de todos los puntos, de\(x \in B \subset \mathbb{R}^n\) tal manera que
\(dist(\phi_{t}(x), M) \rightarrow 0\)como\(t \rightarrow \infty\)
Entonces llamar B se llama la cuenca de atracción de M.
Consideramos ahora un ejemplo que nos permite explorar explícitamente estas ideas.
Ejemplo\(\PageIndex{9}\)
Considere el siguiente campo vectorial autónomo en el plano:
\(\dot{x} = x\),
\[\dot{y} = y^{2}(1-y^2) \equiv f(y), (x, y) \in \mathbb{R}^2. \label{3.10}\]
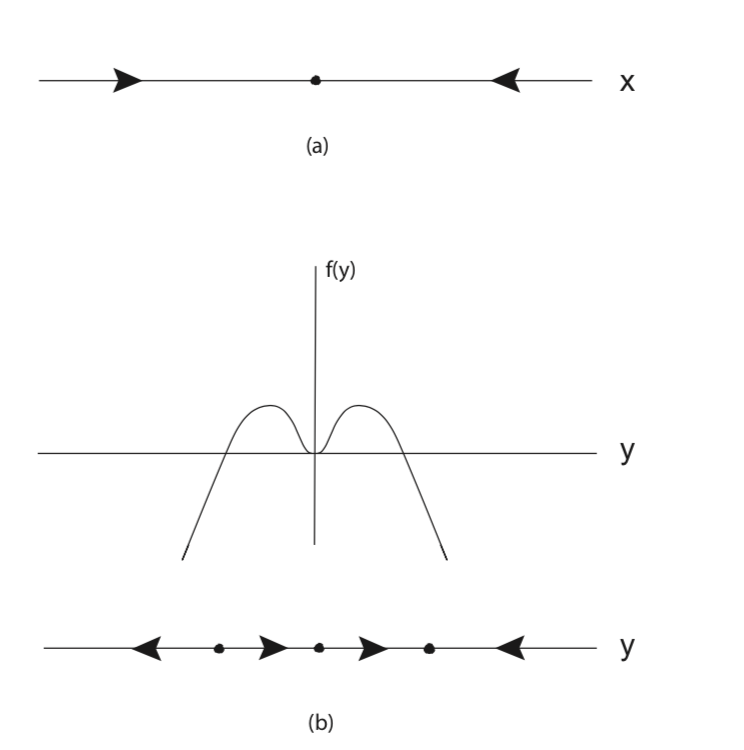
En primer lugar, es útil señalar que los componentes x e y de la Ecuación\ ref {3.10} son independientes. En consecuencia, esto puede parecer un ejemplo trivial. Sin embargo, veremos que tales ejemplos proporcionan una gran cantidad de conocimiento, especialmente porque permiten cálculos simples de muchas de las ideas matemáticas.
En la Fig. 3.1 ilustramos el flujo de los componentes x e y de la Ecuación\ ref {3.10} por separado.
El campo vectorial bidimensional Ecuación\ ref {3.10} tiene puntos de equilibrio en: (x, y) = (0, 0), (0, 1),\((0, -1)\).
En este ejemplo es fácil identificar tres líneas horizontales invariantes (ejemplos de conjuntos invariantes). Ya que y = 0 implica eso\(\dot{y} = 0\), esto implica que el eje x es invariante. Ya que y = 1 implica eso\(\dot{y} = 0\), esto implica que la línea y = 1 es invariante. Ya que\(y = -1\) implica eso\(\dot{y} = 0\), lo que implica que la línea\(y = -1\) es invariante. Esto se ilustra en la Fig. 3.2. A continuación proporcionamos algunos conjuntos invariantes adicionales para (3.10). Es instructivo entender por qué son invariantes, y si hay o no otros conjuntos invariantes.
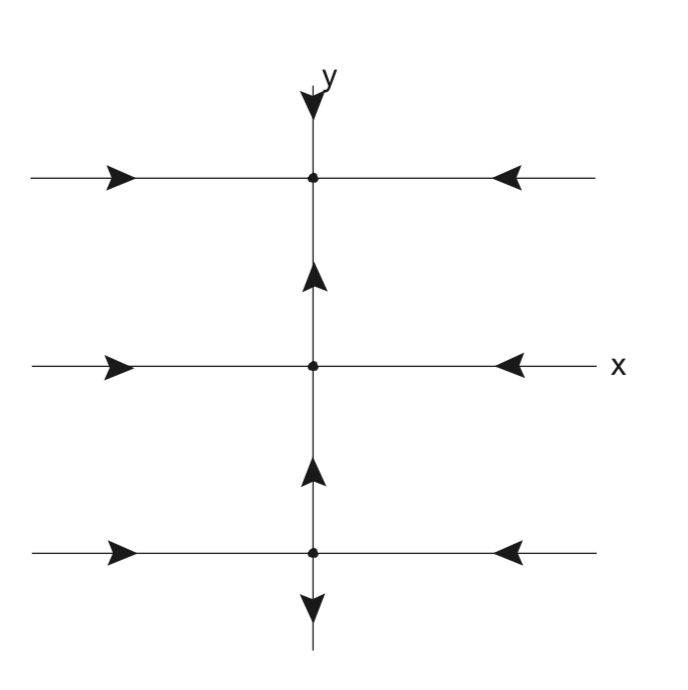
Conjuntos invariantes adicionales para (3.10).
{(x, y) |\(-\infty < x < 0, -\infty < y < 1\)},
{(x, y) |\(0 < x < \infty, -\infty < y < 1\)},
{(x, y) |\(-\infty < x < 0, 1 < y < 0\)},
{(x, y) |\(0 < x < \infty, 1 < y < 0\)},
{(x, y) |\(-\infty < x < 0, 0 < y < 1\)},
{(x, y) |\(0 < x < \infty, 0 < y < 1\)},
{(x, y) |\(-\infty < x < 0, 1 < y < \infty\)},
{(x, y) |\(0 < x < \infty, 1 < y < \infty\)}.


