2.1: Conjunto de problemas

Última actualización
Guardar como PDF

Page ID: 113672

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

EJERCIO$\PageIndex{1}$

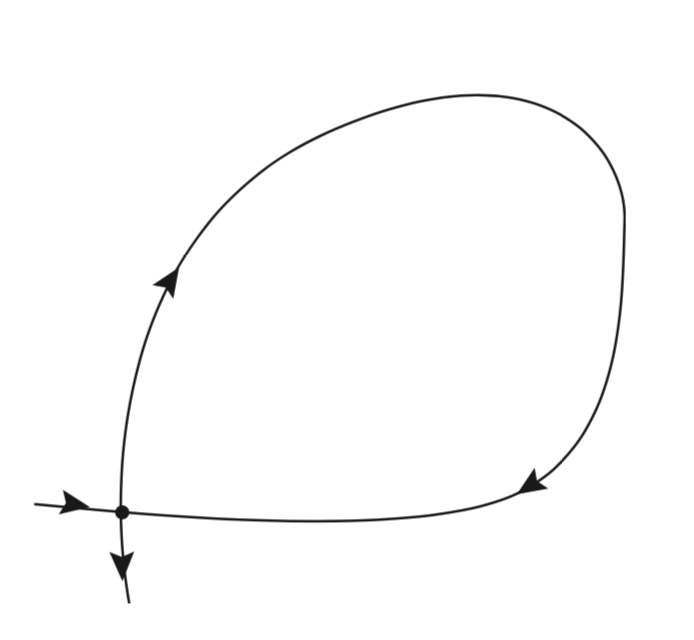
Considera un campo vectorial autónomo en el plano que tiene un punto fijo hiperbólico con una órbita homoclínica que conecta el punto fijo hiperbólico, como se ilustra en la Fig. 1. Asumimos que la existencia y singularidad de las soluciones se mantiene. ¿Puede una trayectoria que comience en algún punto de la órbita homoclínica alcanzar el punto fijo hiperbólico en un tiempo finito? (Debes justificar tu respuesta.)

$Screen Shot 2019-09-12 en 1.37.59 PM.png$

EJERCIO$\PageIndex{2}$

¿Un campo vectorial autónomo sobre el$\mathbb{R}$ que no tiene puntos de equilibrio puede tener órbitas periódicas? Asumimos que la existencia y singularidad de las soluciones se mantiene. (Debes justificar tu respuesta.)

EJERCIO$\PageIndex{3}$

¿Un campo vectorial no autónomo en el$\mathbb{R}$ que no tiene puntos de equilibrio puede tener órbitas periódicas? Asumimos que la existencia y singularidad de las soluciones se mantiene. (Debes justificar tu respuesta.)

EJERCIO$\PageIndex{4}$

¿Puede un campo vectorial autónomo en el círculo que no tiene puntos de equilibrio tener órbitas periódicas? Asumimos que la existencia y singularidad de las soluciones se mantiene. (Debes justificar tu respuesta.)

EJERCIO$\PageIndex{5}$

Considere el siguiente campo vectorial autónomo en el plano:

$\dot{x} = -\omega y$,

$\dot{y} = \omega x$,$(x, y) \in \mathbb{R}^2$,

donde$\omega > 0$

Mostrar que el flujo generado por este campo vectorial viene dado por:
\[\begin{pmatrix} {x(t)}\\{y(t)} \end{pmatrix} = \begin{pmatrix} {cos \omega t}&{-sin \omega t}\\ {sin \omega t}&{cos \omega t} \end{pmatrix} \begin{pmatrix} {x_{0}}\\ {y_{0}} \end{pmatrix} \nonumber\]
Demuestre que el flujo obedece a la propiedad de cambio de tiempo.
Dar la condición inicial para el flujo desplazado en el tiempo.

EJERCIO$\PageIndex{6}$

Considere el siguiente campo vectorial autónomo en el plano:

$\dot{x} = \lambda y$,

$\dot{y} = \lambda x$,$(x, y) \in \mathbb{R}^2$,

Mostrar que el flujo generado por este campo vectorial viene dado por:
\[\begin{pmatrix} {x(t)}\\{y(t)} \end{pmatrix} = \begin{pmatrix} {cosh \lambda t}&{sinh \lambda t}\\ {sinh \lambda t}&{cosh \lambda t} \end{pmatrix} \begin{pmatrix} {x_{0}}\\ {y_{0}} \end{pmatrix} \nonumber\]
Demuestre que el flujo obedece a la propiedad de cambio de tiempo.
Dar la condición inicial para el flujo desplazado en el tiempo.

EJERCIO$\PageIndex{7}$

Mostrar que la propiedad de desplazamiento de tiempo para campos vectoriales autónomos implica que las trayectorias no pueden “cruzarse entre sí”, es decir, cruzarse, en el espacio de fase.

EJERCIO$\PageIndex{8}$

Mostrar que la unión de dos conjuntos invariantes es un conjunto invariante.

EJERCIO$\PageIndex{9}$

Mostrar que la intersección de dos conjuntos invariantes es un conjunto invariante.

EJERCIO$\PageIndex{10}$

Mostrar que el complemento de un conjunto invariante positivo es un conjunto invariante negativo.