9.1: Bifurcación de Equilibrios II
- Page ID
- 113648
Hemos examinado puntos fijos de campos vectoriales autónomos unidimensionales donde la matriz asociada a la linealización del campo vectorial alrededor del punto fijo tiene un valor propio cero. Es natural preguntar “¿hay bifurcaciones más complicadas, y qué las hace complicadas?”
Si se piensa en los ejemplos considerados hasta ahora, hay dos posibilidades que podrían complicar la situación. Una es que podría haber más de un valor propio de la linealización sobre el punto fijo con cero parte real (lo que necesariamente requeriría una consideración de campos vectoriales de dimensiones superiores), y el otro sería la no linealidad más complicada (o una combinación de estos dos). Comprender cómo la dimensionalidad y la no linealidad contribuyen a la “complejidad” de una bifurcación (y lo que eso podría significar) es un tema muy interesante, pero más allá del alcance de este curso. Este es generalmente un tema explorado en cursos de posgrado sobre teoría de sistemas dinámicos que enfatizan la teoría de la bifurcación. Aquí estamos principalmente simplemente introduciendo las ideas básicas y temas con ejemplos que uno podría encontrar en las aplicaciones. Para ello consideraremos un ejemplo de una bifurcación que es muy importante en las aplicaciones: la bifurcación Poincaré-Andronov-Hopf (o simplemente bifurcación Hopf como se le conoce más comúnmente). Se trata de una bifurcación de un punto fijo de un campo vectorial autónomo donde el punto fijo no es hiperbólico como resultado de que el jacobiano tiene un par de valores propios puramente imaginarios,\(\pm i \mathcal{w}, \mathcal{w} \ne 0\). Por lo tanto, este tipo de bifurcación requiere (al menos dos dimensiones), y no se caracteriza por un cambio en el número de puntos fijos, sino por la creación de soluciones periódicas dependientes del tiempo. Analizaremos esta situación considerando un ejemplo específico. Referencias dedicadas únicamente a la bifurcación Hopf son los libros de Marsden y McCracken y Hassard, Kazarinoff y Wan.
Consideramos el siguiente campo vectorial autónomo no lineal en el plano:
\[ \begin{align} \dot{x} &= \mu x- \mathcal{w}y+(ax-by)(x^2+y^2) \\[4pt] \dot{y} &= \mathcal{w}x+\mu y+(bx+ay)(x^2+y^2), (x, y) \in \mathbb{R}^2, \label{9.1} \end{align}\]
donde consideramos\(a\),\(b\),\(\mathcal{w}\) como constantes fijas y\(\mu\) como un parámetro variable. El origen, (x, y) = (0, 0) es un punto fijo, y queremos considerar su estabilidad. La matriz asociada a la linealización sobre el origen viene dada por:
\[\begin{pmatrix} {\mu}&{\mathcal{-w}}\\ {\mathcal{w}}&{\mu} \end{pmatrix}, \label{9.2}\]
y sus valores propios están dados por:
\[\lambda_{1, 2} = \mu \pm i\mathcal{w}. \label{9.3}\]
Por lo tanto, en función\(\mu\) del origen tiene las siguientes propiedades de estabilidad:
\[\left\{ \begin{array}{ll} {\mu < 0}&{\text{sink}}\\ {\mu = 0}&{\text{center}}\\ {\mu > 0}&{\text{source}} \end{array} \right. \label{9.4}\]
El origen no es hiperbólico en\(\mu = 0\), y hay un cambio en la estabilidad a medida que\(\mu\) los cambios se manifiestan. Queremos analizar el comportamiento cerca del origen, tanto en el espacio de fase como en el espacio de parámetros, con más detalle.
Hacia este fin transformamos la Ecuación\ ref {9.1} en coordenadas polares usando la relación estándar entre las coordenadas cartesianas y polares:
\[x = r\cos \theta, y = r\sin \theta \label{9.5}\]
Diferenciar estas dos expresiones con respecto a t, y sustituirlas en la Ecuación\ ref {9.1} da:
\[\dot{x} = \dot{r} \cos \theta - r\dot{\theta}\sin \theta = \mu r \cos \theta - \mathcal{w} r \sin \theta + (ar \cos \theta - br \sin \theta)r^2, \label{9.6}\]
\[\dot{y} = \dot{r} \cos \theta + r\dot{\theta}\sin \theta = \mathcal{w} r \cos \theta - \mu r \sin \theta + (br \cos \theta - ar \sin \theta)r^2, \label{9.7}\]
a partir de la cual obtenemos las siguientes ecuaciones para\(\dot{r}\) y
\[\dot{r} = \mu r+ar^3, \label{9.8}\]
\[r\dot{\theta} = \mathcal{w}r + br^3, \label{9.9}\]
donde la Ecuación\ ref {9.8} se obtiene multiplicando la Ecuación\ ref {9.6} por\(\cos \theta\) y la Ecuación\ ref {9.7} por\(\sin \theta\) y sumando los dos resultados, y la Ecuación\ ref {9.9} se obtiene multiplicando la Ecuación\ ref {9.6} por\(sin \theta\) y (9.7) por\(cos \theta\) y sumando los dos resultados. Dividiendo ambas ecuaciones por\(r\) da las dos ecuaciones que analizaremos:
\[\dot{r} = \mu r+ar^3, \label{9.10}\]
\[\dot{\theta} = \mathcal{w} + br^2, \label{9.11}\]
Tenga en cuenta que la Ecuación\ ref {9.10} tiene la forma de la bifurcación de la horca que estudiamos anteriormente. Sin embargo, es muy importante darnos cuenta de que estamos tratando con las ecuaciones en coordenadas polares y entender lo que nos revelan sobre la dinámica en las coordenadas cartesianas originales. Para empezar, debemos tenerlo presente\(r \ge 0\).
Tenga en cuenta que la Ecuación\ ref {9.10} es independiente de\(\theta\), es decir, es una ODE unidimensional y autónoma que reescribimos a continuación:
\[\dot{r} = \mu r+ar^3 =r(\mu+ar^2). \label{9.12}\]
Los puntos fijos de esta ecuación son:
\[r = 0, r = \sqrt{-\frac{\mu}{a}} \equiv r^{+}. \label{9.13}\]
(Tenga en cuenta eso\(r \ge 0\).) Sustituyendo\(r^{+}\) en Ecuaciones\ ref {9.10} y\ ref {9.11} da:
\(\dot{r^{+}} = \mu r^{+}+ar^{+3} = 0\),
\[\dot{\theta} = \mathcal{w}r + b(-\frac{\mu}{a}), \label{9.14}\]
El\(\theta\) componente se puede resolver fácilmente (usando\(r^{+} = -\frac{\mu}{a}\)), después de lo cual obtenemos:
\[\theta (t) = (\mathcal{w}- \frac{\mu b}{a}) + \theta(0). \label{9.15}\]
Por lo tanto\(r\) no cambia en el tiempo a\(r = r^{+}\) y q evoluciona linealmente en el tiempo. Pero\(\theta\) es una coordenada angular. Esto implica que\(r = r^{+}\) corresponde a una órbita periódica.
Con esta información, analizamos el comportamiento de la Ecuación\ ref {9.12} mediante la construcción del diagrama de bifurcación. Hay dos casos a considerar:\(a > 0\) y\(a < 0\).
En la figura 9.1 se esbozan los ceros de (9.12) en función de\(\mu\) para a > 0. Vemos que una órbita periódica se bifurca desde el punto fijo no hiperbólico en\(\mu = 0\). La órbita periódica es inestable y existe para\(\mu < 0\). En la Fig. 9.2 se ilustra la dinámica en el plano de\(x - y\) fase.
En la figura 9.3 esbozamos los ceros de la Ecuación\ ref {9.12} en función de\(\mu\) para a < 0. Vemos que una órbita periódica se bifurca desde el punto fijo no hiperbólico en\(\mu = 0\). La órbita periódica es estable en este caso y existe para\(\mu > 0\). En la Fig. 9.4 ilustramos la dinámica en el plano de\(x - y\) fase.
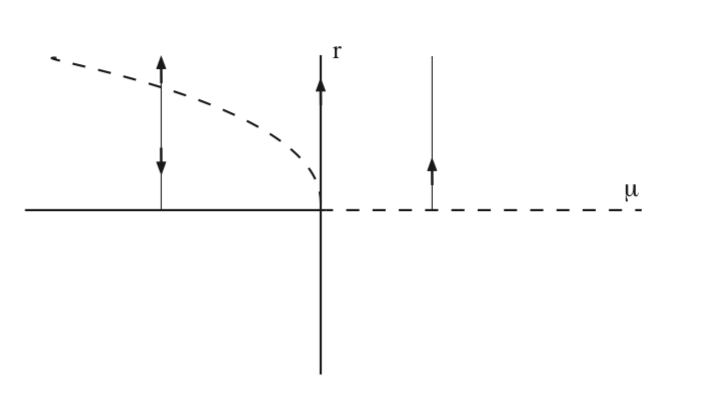
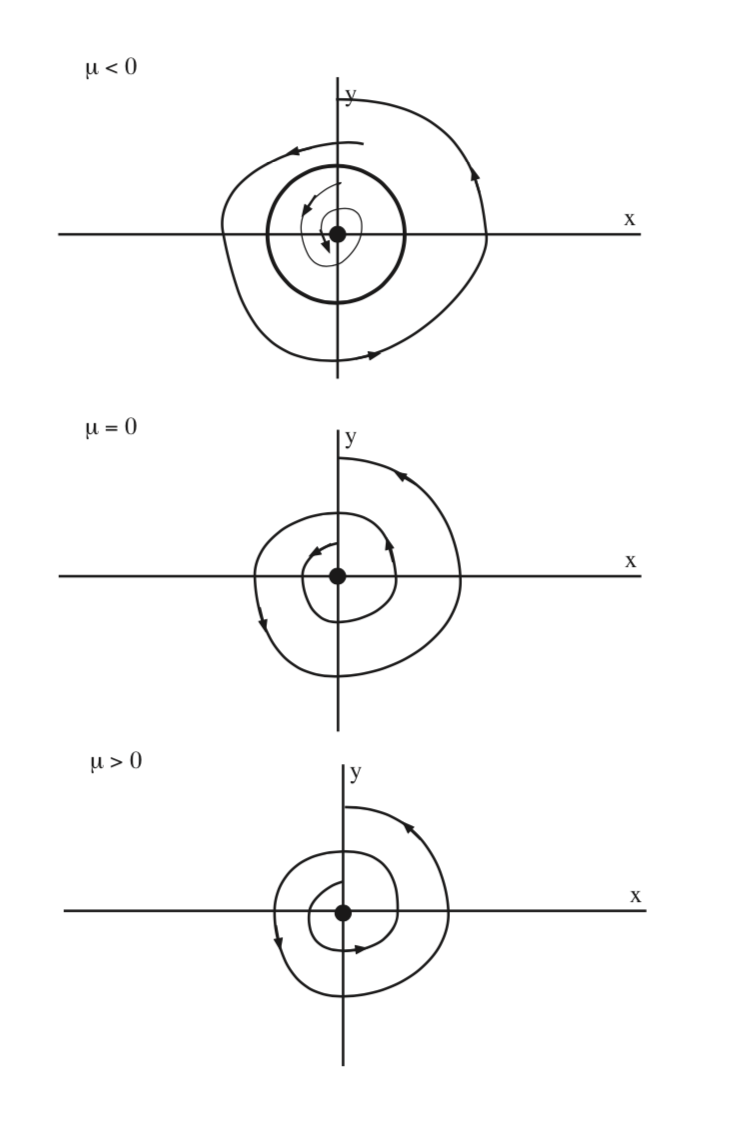
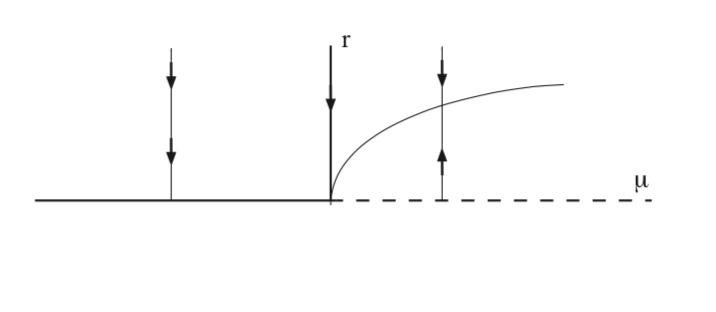
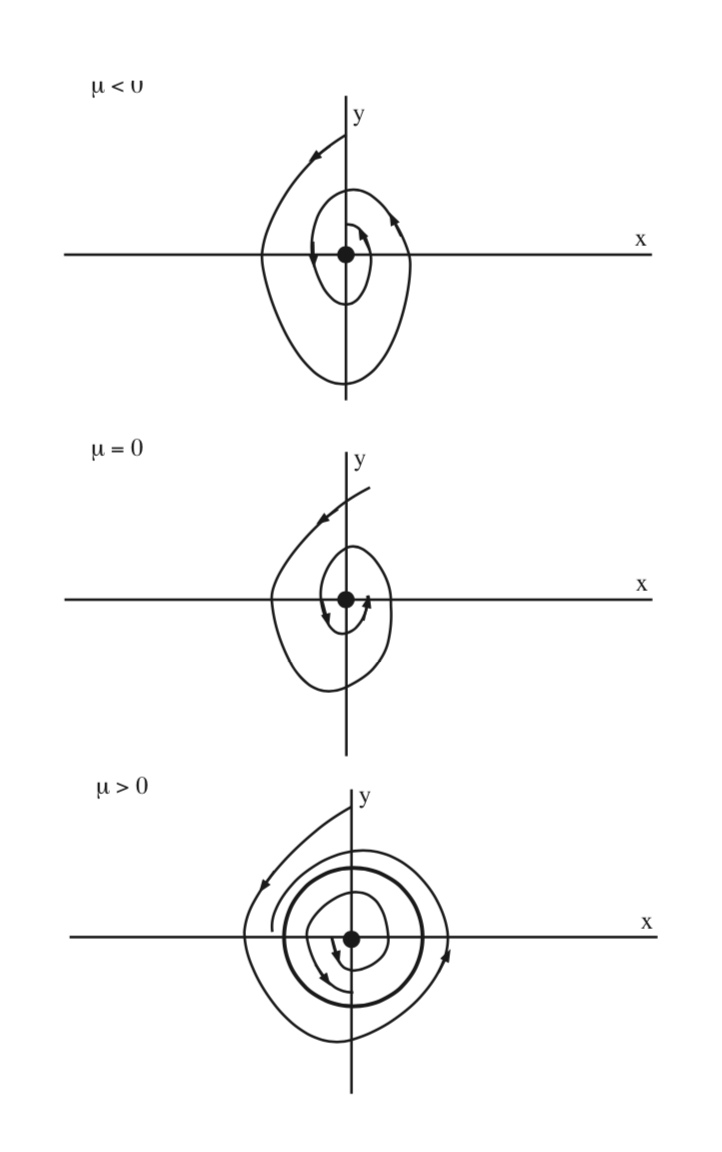
En este ejemplo hemos visto que un punto fijo no hiperbólico de un campo vectorial autónomo bidimensional, donde la no hiperbolicidad surge del hecho de que la linealización en el punto fijo tiene un par de valores propios imaginarios puros,\(\pm i\mathcal{w}\), puede conducir a la creación de órbitas periódicas como parámetro es variado. Este es un ejemplo de lo que generalmente se llama la bifurcación Hopf. Es el primer ejemplo que hemos visto de la bifurcación de una solución de equilibrio que resulta en soluciones dependientes del tiempo.
En este punto es útil resumir la naturaleza de las condiciones que resultan en una bifurcación Hopf para un campo vectorial autónomo bidimensional. Para empezar, necesitamos un punto fijo donde el jacobiano asociado a la linealización sobre el punto fijo tenga un par de valores propios imaginarios puros. Esta es una condición necesaria para la bifurcación Hopf. Ahora, al igual que para las bifurcaciones de puntos fijos de campos vectoriales autónomos unidimensionales (por ejemplo, las bifurcaciones de nodo de silla de montar, transcrítica y horca que hemos estudiado en el capítulo anterior), se determina la naturaleza de la bifurcación para valores de parámetros en una vecindad del parámetro de bifurcación por la forma de la no linealidad del campo vectorial. Desarrollamos la idea de la bifurcación Hopf en el contexto de la Ecuación\ ref {9.1}, y en ese ejemplo la estabilidad de la órbita periódica bifurcada estuvo dada por el signo del coeficiente a (estable para un < 0, unstable for a > 0). En el ejemplo, el coeficiente de estabilidad Âa Z ́a Z ́a Z ́era evidente a partir de la estructura simple de la no linealidad. En ejemplos más complicados, es decir, términos no lineales más complicados, la determinación del coeficiente de estabilidad es más Âa Z ́algebraicamente intensiva ÂA Z ́Âa Z ́a. Las expresiones explícitas para el coeficiente de estabilidad se dan en muchos textos de sistemas dinámicos. Por ejemplo, se da en Guckenheimer y Holmes y Wiggins. Los detalles completos del cálculo del coeficiente de estabilidad se llevan a cabo en 7. El problema 2 al final de este capítulo explora la naturaleza de la bifurcación Hopf, por ejemplo, el número y la estabilidad de órbitas periódicas bifurcadas, para diferentes formas de no linealidad.
A continuación, volvemos a los ejemplos de bifurcaciones de puntos fijos en campos vectoriales unidimensionales y damos dos ejemplos de campos vectoriales unidimensionales donde puede ocurrir más de una de las bifurcaciones que discutimos anteriormente.
Ejemplo\(\PageIndex{27}\)
Considere el siguiente campo vectorial autónomo unidimensional dependiendo de un parámetro\(\mu\):
\[\dot{x} = \mu-\frac{x^2}{2}+\frac{x^3}{3} , x \in \mathbb{R}. \label{9.16}\]
Los puntos fijos de este campo vectorial vienen dados por:
\[\mu = \frac{x^2}{2}-\frac{x^3}{3}, \label{9.17}\]
y se representan en la Fig. 9.5.
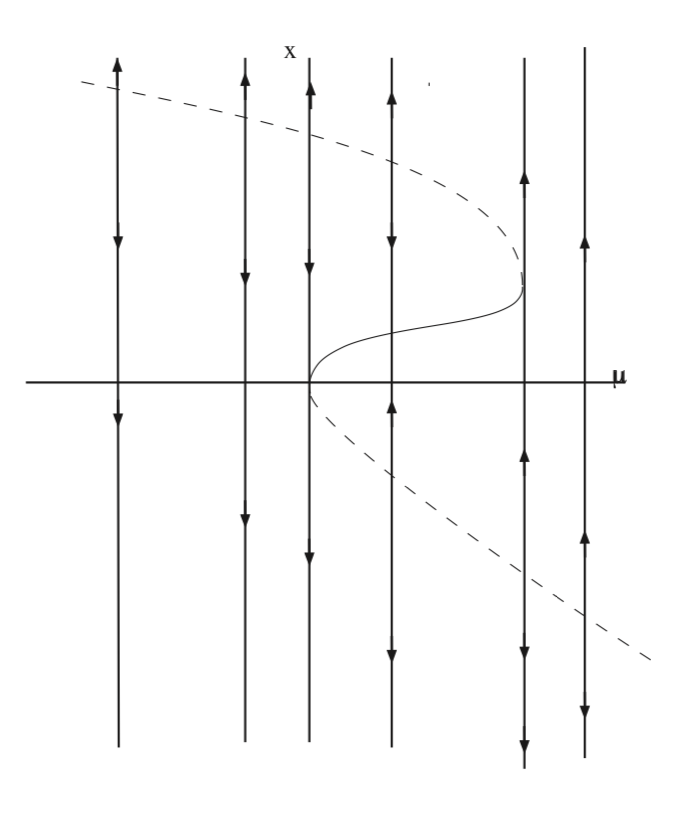
La curva trazada es donde el campo vectorial es cero. De ahí que sea positivo a la derecha de la curva y negativo a la izquierda de la curva. De esto concluimos la estabilidad de los puntos fijos como se muestra en la figura.
Hay dos bifurcaciones de nodo de silla de montar que ocurren donde\(\frac{d \mu}{dx} (x) = 0\). Estos se encuentran en
\[(x, \mu) = (0, 0), (1,\frac{1}{6}). \label{9.18}\]
Ejemplo\(\PageIndex{28}\)
Considere el siguiente campo vectorial autónomo unidimensional dependiendo de un parámetro\(\mu\):
\(\dot{x} = \mu x-\frac{x^3}{2}+\frac{x^4}{3}\),
\[= x(\mu-\frac{x^2}{2}+\frac{x^3}{3}), \label{9.19}\]
Los puntos fijos de este campo vectorial vienen dados por:
\[\mu = \frac{x^2}{2}-\frac{x^3}{3}, \label{9.20}\]
y
\[x = 0, \label{9.21}\]
y se representan en el\(\mu - x\) plano en la Fig. 9.6.
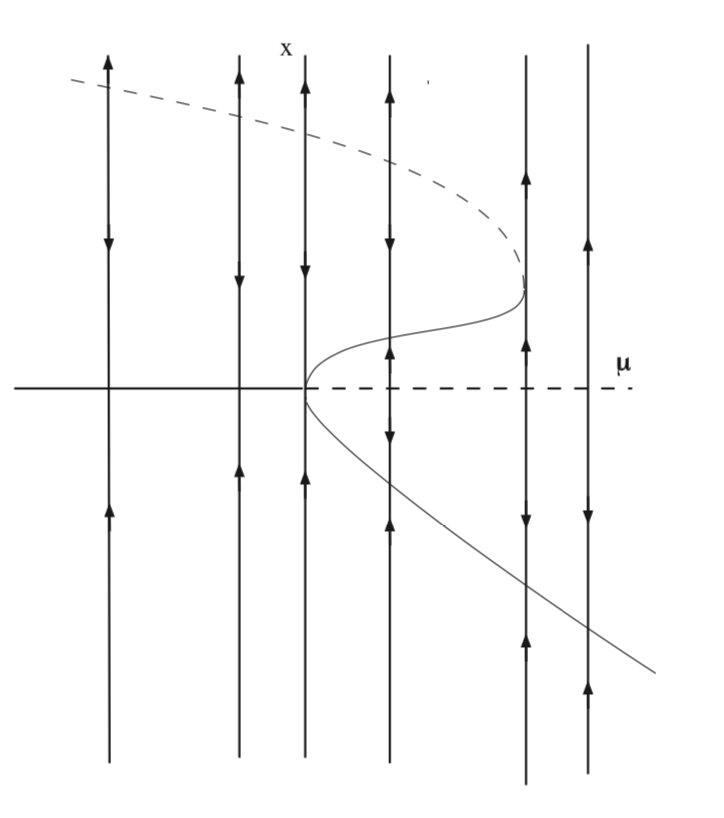
En este ejemplo vemos que hay una bifurcación de horca y una bifurcación de nodo de silla de montar.


