11.5: E- Dinámica de las ecuaciones de Hamilton

En este apéndice damos una breve introducción a algunas de las características y resultados asociados con las ecuaciones diferenciales hamiltonianas (o, las ecuaciones de Hamilton o campos vectoriales hamiltonianos). La formulación hamiltoniana de las ecuaciones de Newton revela una gran cantidad de estructura sobre la dinámica y también da lugar a una gran cantidad de matemáticas profundas que es el foco de gran parte de la investigación contemporánea.

Nuestro propósito aquí no es derivar las ecuaciones de Hamilton de las ecuaciones de Newton. Las discusiones sobre eso se pueden encontrar en muchos libros de texto sobre mecánica (aunque a menudo se la considera ''mecánica avanzada”). Por ejemplo, una exposición clásica de este tema se puede encontrar en el libro clásico de Landau, y exposiciones más modernas se pueden encontrar en Abraham y Marsden y Arnold. Más bien, nuestro enfoque es comenzar con las ecuaciones de Hamilton y comprender algunos aspectos simples y consecuencias de la estructura especial asociada a las ecuaciones de Hamilton. Hacia este fin, nuestro punto de partida serán las ecuaciones de Hamilton. Siguiendo el enfoque simple a lo largo de estas conferencias, nuestra discusión sobre las ecuaciones de Hamilton será para sistemas bidimensionales.

Comenzamos con una función de valor escalar definida en\(\mathbb{R}^2\)

\[H = H(q, p), (q, p) \in \mathbb{R}^2. \label{E.1}\]

Esta función es referida como la hamiltoniana. Del hamiltoniano, las ecuaciones de Hamilton toman la siguiente forma:

\(\dot{q} = \frac{\partial H}{\partial p} (q, p)\),

\[\dot{p} = \frac{\partial H}{\partial q}(q, p), (q, p) \in \mathbb{R}^2. \label{E.2}\]

La forma de las ecuaciones de Hamilton implica que el hamiltoniano es constante en las trayectorias. Esto se puede ver a partir del siguiente cálculo:

\(\frac{dH}{dt} = \frac{\partial H}{\partial q} \dot{q} +\frac{\partial H}{\partial p} \dot{p}\)

\[= \frac{\partial H}{\partial q} \frac{\partial H}{\partial p} - \frac{\partial H}{\partial p} \frac{\partial H}{\partial q} = 0. \label{E.3}\]

Además, este cálculo implica que los conjuntos de niveles del hamiltoniano son colectores invariantes. Denotamos el conjunto de niveles del hamiltoniano como:

\[H_{E} = \{(q, p) \in \mathbb{R}^2 | H(q, p) = E\} \label{E.4}\]

En general, el conjunto de niveles es una curva (o posiblemente un punto de equilibrio). De ahí que en el caso bidimensional, las trayectorias de las ecuaciones de Hamilton están dadas por los conjuntos de niveles del hamiltoniano.

El jacobiano del campo vectorial hamiltoniano (E.2), denotado J, viene dado por:

\[J(p, q) = \begin{pmatrix} {\frac{\partial^{2}H}{\partial q \partial p}}&{\frac{\partial^{2}H}{\partial p^2}}\\ {-\frac{\partial^{2}H}{\partial q^2}}&{-\frac{\partial^{2}H}{\partial p \partial q}} \end{pmatrix}, \label{E.5}\]

en un punto arbitrario\((q, p) \in \mathbb{R}^2\). Obsérvese que la traza de J (q, p), denotada TRj (q, p), es cero. Esto implica que los valores propios de J (q, p), denotados por\(\lambda_{1, 2}\), están dados por:

\[\lambda_{1, 2} = \pm \sqrt{-det J(q, p)}, \label{E.6}\]

donde detJ (q, p) denota el determinante de J (q, p). Por lo tanto, si\((q_{0}, p_{0})\) es un punto de equilibrio de (E.1) y\(detJ(q_{0}, p_{0}) = 0\), entonces el punto de equilibrio es un centro para\(detJ(q_{0}, p_{0}) > 0\) y una silla de montar para\(detJ(q_{0}, p_{0}) < 0\).

A continuación se describen algunos ejemplos de campos vectoriales hamiltonianos bidimensionales y lineales autónomos.

Ejemplo\(\PageIndex{41}\) (The Hamiltonian Saddle )

Consideramos al hamiltoniano:

\[H(q, p) = \frac{\lambda}{2} (p^{2}-q^{2}) = \frac{\lambda}{2} (p-q)(p+q), (q, p) \in \mathbb{R}^2, \label{E.7}\]

con\(\lambda > 0\). De este hamiltoniano, derivamos las ecuaciones de Hamilton:

\(\dot{q} = \frac{\partial H}{\partial p} (q, p) = \lambda p\),

\[\dot{p} = \frac{\partial H}{\partial p} (q, p) = \lambda q, \label{E.8}\]

o en forma de matriz:

\[\begin{pmatrix} {\dot{q}}\\ {\dot{p}} \end{pmatrix} = \begin{pmatrix} {0}&{\lambda}\\ {\lambda}&{0} \end{pmatrix} \begin{pmatrix} {q}\\ {p} \end{pmatrix}. \label{E.9}\]

El origen es un punto fijo, y los valores propios asociados a la linealización vienen dados por\(\pm \lambda\). De ahí que el origen sea un punto de silla.El valor del hamiltoniano en el origen es cero. También vemos de (E.7) que el hamiltoniano es cero en las líneas\(p - q = 0\) y p + q = 0. Estos son los colectores inestables y estables del origen, respectivamente. El retrato de fase se ilustra en la Fig. E.1.

Figura E.1: Retrato de fase del sillín lineal hamiltoniano. El colector estable del origen viene dado por\(p-q = 0\) y el colector inestable del origen viene dado por p + q = 0.

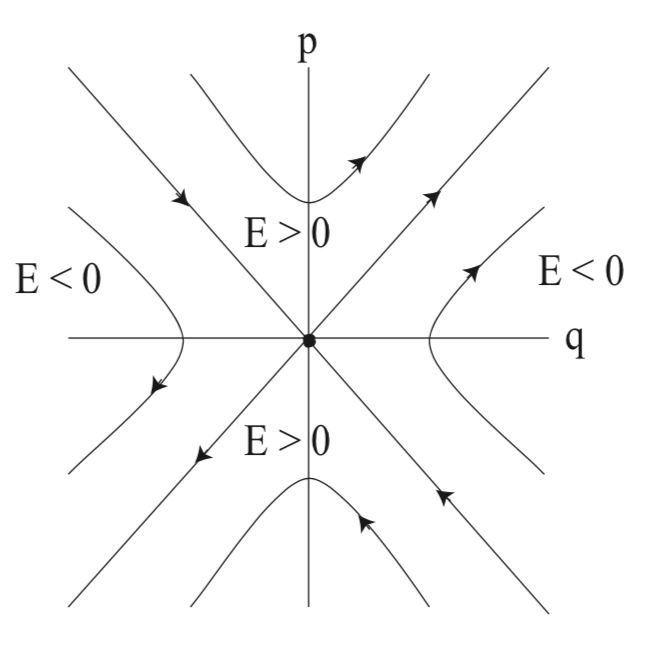
El flujo generado por este campo vectorial se da en el Capítulo 2, Conjunto de Problemas 2, problema 6.

Ejemplo\(\PageIndex{42}\) (The Hamiltonian Center)

Consideramos al hamiltoniano:

\[H(q, p) = \frac{\omega}{2} (p^{2}+q^{2}), (q, p) \in \mathbb{R}^2, \label{E.10}\]

con\(\omega > 0\). De este hamiltoniano, derivamos las ecuaciones de Hamilton:

\(\dot{q} = \frac{\partial H}{\partial p} (q, p) = \omega p\),

\[\dot{p} = \frac{\partial H}{\partial p} (q, p) = -\omega q, \label{E.11}\]

o en forma de matriz:

\[\begin{pmatrix} {\dot{q}}\\ {\dot{p}} \end{pmatrix} = \begin{pmatrix} {0}&{\omega}\\ {-\omega}&{0} \end{pmatrix} \begin{pmatrix} {q}\\ {p} \end{pmatrix}. \label{E.12}\]

Los conjuntos de niveles del hamiltoniano son círculos, y se ilustran en la Fig. E.2.

Figura E.2: El retrato de fase para el centro hamiltoniano lineal.

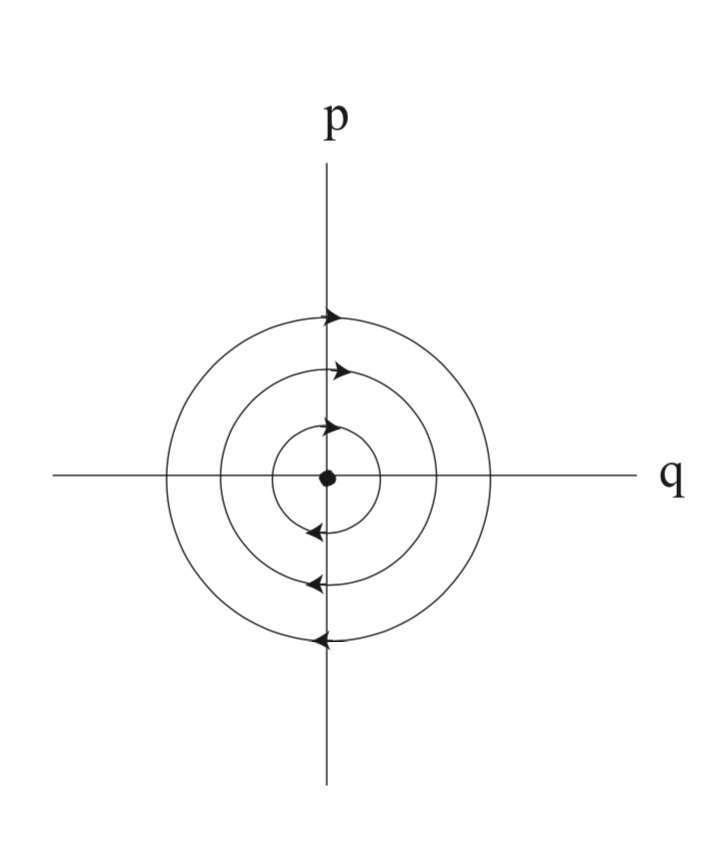
El flujo generado por este campo vectorial se da en el Capítulo 2, Conjunto de Problemas 2, problema 5.

Consideraremos ahora dos ejemplos de bifurcación de equilibrios en sistemas hamiltonianos bidimensionales. La bifurcación asociada a un valor propio cero (como estudiamos en el Capítulo 8) no es posible ya que, siguiendo (E.6), si hay un valor propio cero el otro valor propio también debe ser cero. Consideraremos ejemplos de las bifurcaciones hamiltonianas de nodo-silla y horca hamiltoniana. Las discusiones sobre las versiones hamiltonianas de estas bifurcaciones también se pueden encontrar en Golubitsky et al.

Ejemplo\(\PageIndex{43}\) (Hamiltonian saddle-node bifurcation)

Consideramos al hamiltoniano:

\[H(q, p) = \frac{p^2}{2} - \lambda q+\frac{q^{3}}{3}), (q, p) \in \mathbb{R}^2, \label{E.13}\]

donde\(\lambda\) se considera un parámetro que puede ser variado. De este hamiltoniano, derivamos las ecuaciones de Hamilton:

\(\dot{q} = \frac{\partial H}{\partial p} (q, p) = p\),

\[\dot{p} = -\frac{\partial H}{\partial p} (q, p) = \lambda - q^2, \label{E.14}\]

Los puntos fijos para (E.14) son:

\[(q, p) = (\pm \sqrt{\lambda}, 0), \label{E.15}\]

de lo que se deduce que no hay puntos fijos para\(\lambda < 0\), un punto fijo para\(\lambda = 0\), y dos puntos fijos para\(\lambda > 0\). Este es el escenario para una bifurcación de nodo de silla de montar.

A continuación examinamos la estabilidad de los puntos fijos. El jacobiano de (E.14) viene dado por:

\[\begin{pmatrix} {0}&{1}\\ {-2q}&{0} \end{pmatrix}. \label{E.16}\]

Los valores propios de esta matriz son:

\(\lambda_{1, 2} = \pm \sqrt{-2q}\).

De ahí\((q, p) = (-\sqrt{\lambda}, 0)\) que sea una silla de montar,\((q, p) = (\sqrt{\lambda}, 0)\) es un centro, y (q, p) = (0, 0) tiene dos valores propios cero. Los retratos de fase se muestran en la Fig. E.3.

Figura E.3: Los retratos de fase para la bifurcación hamiltoniana de la silla de montar.

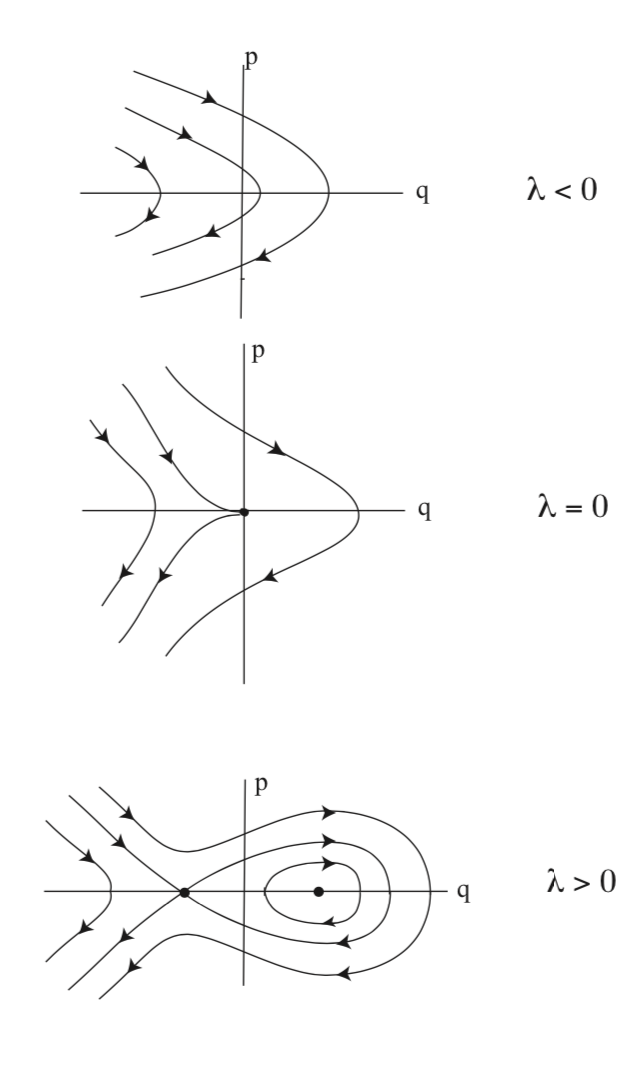
Ejemplo\(\PageIndex{44}\) (Hamiltonian pitchfork bifurcation)

Consideramos al hamiltoniano:

\[H(q, p) = \frac{p^2}{2} - \lambda \frac{q^2}{2}+\frac{q^{4}}{4}), (q, p) \in \mathbb{R}^2, \label{E.17}\]

donde\(\lambda\) se considera un parámetro que puede ser variado. De este hamiltoniano, derivamos las ecuaciones de Hamilton:

\(\dot{q} = \frac{\partial H}{\partial p} (q, p) = p\),

\[\dot{p} = -\frac{\partial H}{\partial p} (q, p) = \lambda q - q^3, \label{E.18}\]

Los puntos fijos para (E.18) son:

\[(q, p) = (0, 0), (\pm p\lambda, 0), \label{E.19}\]

de lo que se deduce que hay un punto fijo para\(\lambda < 0\), un punto fijo para\(\lambda = 0\), y tres puntos fijos para\(\lambda > 0\). Este es el escenario para una bifurcación de horca.

A continuación examinamos la estabilidad de los puntos fijos. El jacobiano de (E.18) viene dado por:

\[\begin{pmatrix} {0}&{1}\\ {\lambda-3q^2}&{0} \end{pmatrix}. \label{E.20}\]

Los valores propios de esta matriz son:

\(\lambda_{1,2} = \pm \sqrt{\lambda-3q^2}\).

De ahí que (q, p) = (0, 0) es un centro para\(\lambda < 0\), un sillín para\(\lambda > 0\) y tiene dos valores propios cero para\(\lambda = 0\). Los puntos fijos\((q, p) = (p\lambda, 0)\) son centros para\(\lambda > 0\). Los retratos de fase se muestran en la Fig. E.4.

Figura E.4: Los retratos de fase para la bifurcación de la horca hamiltoniana.

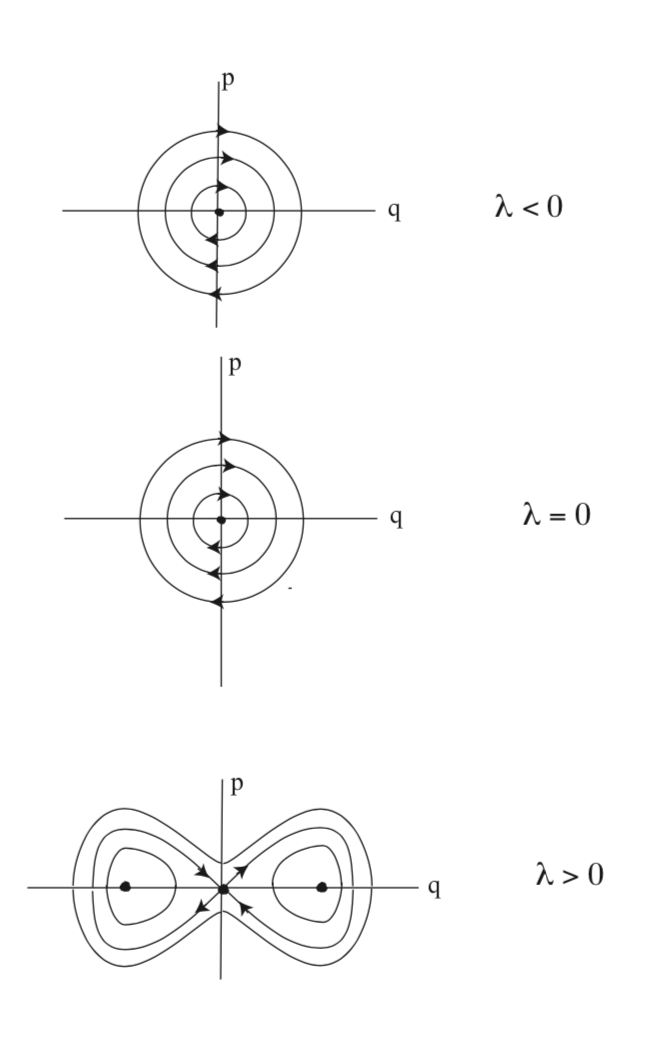
Observamos que, con un poco de pensamiento, debería quedar claro que en dos dimensiones no existe un análogo de la bifurcación Hopf para campos vectoriales hamiltonianos similar a la situación que analizamos anteriormente en el contexto no hamiltoniano. Existe una situación que se conoce como la bifurcación hamiltoniana Hopf, pero esta noción requiere al menos cuatro dimensiones, ver Van Der Meer.

En los sistemas hamiltonianos un parámetro de bifurcación natural es el valor del conjunto de niveles del hamiltoniano, o la “energía”. Desde este punto de vista quizás un candidato más natural para una bifurcación Hopf en un sistema hamiltoniano es descrito por el teorema del subcentro de Lyapunov, véase Kelley. El ajuste de este teorema también requiere al menos cuatro dimensiones, pero los fenómenos asociados ocurren con bastante frecuencia en las aplicaciones.