1.1: Integrales como soluciones
- Page ID
- 115479
Una ODE de primer orden es una ecuación de la forma
\[\dfrac{dy}{dx}=f(x,y) \nonumber \]
o simplemente
\[y'=f(x,y) \nonumber \]
En general, no existe una fórmula o procedimiento sencillo que uno pueda seguir para encontrar soluciones. En las próximas conferencias veremos casos especiales donde las soluciones no son difíciles de obtener. En esta sección, supongamos que\(f\) es una función de\(x\) solo, es decir, la ecuación es
\[y'=f(x) \label{1.1.1} \]
Podríamos simplemente integrar (antidiferenciar) ambos lados con respecto a\(x\).
\[\int y' (x) dx = \int f(x) dx + C \nonumber \]
es decir
\[y(x)=\int f(x) dx + C \nonumber \]
Esta\(y(x)\) es en realidad la solución general. Entonces para resolver Ecuación\(\ref{1.1.1}\), encontramos alguna antiderivada de\(f(x)\) y luego agregamos una constante arbitraria para obtener la solución general.
Ahora es un buen momento para discutir un punto sobre la notación y terminología del cálculo. Los libros de texto de cálculo enturbian las aguas al hablar de la integral como principalmente la llamada integral indefinida. La integral indefinida es realmente la antiderivada (de hecho, toda la familia de antiderivados de un parámetro). Realmente existe solo una integral y esa es la integral definitiva. La única razón de la notación integral indefinida es que siempre podemos escribir una antiderivada como una integral (definida). Es decir, por el teorema fundamental del cálculo siempre podemos escribir\(\int f(x) dx + C\) como
\[\int_{x_0}^x f(t) dt + C \nonumber \]
De ahí la terminología para integrar cuando realmente podemos significar antidiferenciar. La integración es solo una forma de calcular el antiderivado (y es una forma que siempre funciona, ver los siguientes ejemplos). La integración se define como el área bajo la gráfica, solo pasa a computar también antiderivados. En aras de la consistencia, seguiremos usando la notación integral indefinida cuando queramos una antiderivada, y siempre se debe pensar en la integral definida.
Encuentre la solución general de\(y' = 3x^2\).
Solución
El cálculo elemental nos dice que la solución general debe ser\(y = x^3 + C\). Comprobemos:\(y' = 3x^2\). Precisamente hemos conseguido nuestra ecuación de vuelta.
Normalmente, también tenemos una condición inicial como\(y(x_0) = y_0\) para unos dos números\({x_0}\) y\({y_0}\)\({x_0}\) suele ser 0, pero no siempre). Entonces podemos escribir la solución como una integral definitiva de una manera agradable. Supongamos que nuestro problema es\(y' = f(x), \, y(x_0) = y_0\). Entonces la solución es
\[y(x) = \int_{x_0}^x f(s) ds + y_0 \label{1.1.2} \]
¡Comprobemos! Calculamos\(y' = f(x)\), a través del teorema fundamental del cálculo, y por Júpiter,\(y\) es una solución. ¿Es el que satisface la condición inicial? Bueno,\(y(x_0) = \int_{x_0}^{x_0} f(x) dx + y_0 = y_0\). ¡Lo es!
Tenga en cuenta que la integral definida y la integral indefinida (antidiferenciación) son bestias completamente diferentes. La integral definida siempre evalúa a un número. Por lo tanto, Ecuación\(\ref{1.1.2}\) es una fórmula que podemos conectar a la calculadora o a una computadora, y estará encantado de calcular valores específicos para nosotros. Fácilmente podremos trazar la solución y trabajar con ella igual que con cualquier otra función. No es tan crucial encontrar siempre una forma cerrada para el antiderivado.
Resolver
\[y' = e^{-x^2}, ~~ y(0) = 1. \nonumber \]
Por la discusión anterior, la solución debe ser
\[y(x) = \int_0^x e^{-s^2} ds + 1. \nonumber \]
Solución
Aquí tienes una buena manera de burlarte de tus amigos tomando el cálculo del segundo semestre. Dígales que encuentren la solución de forma cerrada. Ja, ja, ja (broma de malas matemáticas). No es posible (en forma cerrada). No hay absolutamente nada de malo en escribir la solución como una integral definitiva. Esta integral en particular es de hecho muy importante en la estadística.
Usando este método, también podemos resolver ecuaciones de la forma
\[y' = f(y) \nonumber \]
Escribamos la ecuación en notación Leibniz.
\[\dfrac{dy}{dx} = f(y) \nonumber \]
Ahora usamos el teorema de la función inversa del cálculo para cambiar los roles de\(x\) y\(y\) obtener
\[\dfrac{dy}{dx} = \dfrac{1}{f(y)} \nonumber \]
Lo que estamos haciendo parece álgebra con\(dx\) y\(dy\). Es tentador simplemente hacer álgebra con\(dx\) y\(dy\) como si fueran números. Y en este caso sí funciona. Sin embargo, tenga cuidado, ya que este tipo de cálculo de agitar las manos puede generar problemas, especialmente cuando hay más de una variable independiente involucrada. En este punto podemos simplemente integrar,
\[x(y) = \int \dfrac{1}{f(y)} dy + C \nonumber \]
Por último, tratamos de resolver para\(y\).
Anteriormente, supusimos\(y' = ky\) (para algunos\(k > 0\)) tiene la solución\(y = Ce^{kx}\). Ahora podemos encontrar la solución sin adivinar. Primero señalamos que\(y = 0\) es una solución. En adelante, asumimos\(y \ne 0\). Escribimos
\[\dfrac{dx}{dy} = \dfrac{1}{ky} \nonumber \]
Nos integramos para obtener
\[x(y) = x = \dfrac{1}{k} \ln \left\vert y \right\vert + D \nonumber \]
donde\(D\) es una constante arbitraria. Ahora resolvemos para\(y\) (en realidad para\(\left\vert y \right\vert\)).
\[\left\vert y \right\vert = e^{kx-kD} = e^{-kD}e^{kx} \nonumber \]
Si reemplazamos\(e^{-kD}\) con una constante arbitraria\(C\) podemos deshacernos de las barras de valor absoluto (lo que podemos hacer como\(D\) fue arbitrario). De esta manera, también incorporamos la solución\(y = 0\). Obtenemos la misma solución general que adivinamos antes,\(y = Ce^{kx}\).
Encuentra la solución general de\(y' = y^2\).
Solución
Primero señalamos que\(y = 0\) es una solución. Ahora podemos asumir eso\(y \ne 0\). Escribir
\[\dfrac{dx}{dy} = \dfrac{1}{y^2} \nonumber \]
Nos integramos para obtener
\[x = \dfrac{-1}{y} + C \nonumber \]
Resolvemos para\(y = \dfrac{1}{C-x}\). Entonces la solución general es
\[y = \dfrac{1}{C-x} \,\, or\,\, y=0 \nonumber \]
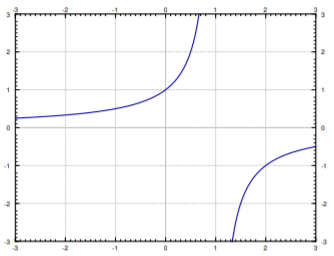
Tenga en cuenta las singularidades de la solución. Si por ejemplo\(C=1\), entonces la solución a medida que nos acercamos\(x=1\). Ver Figura\(\PageIndex{1}\). Generalmente, es difícil distinguir con solo mirar la ecuación misma cómo se va a comportar la solución. La ecuación\(y' = y^2\) es muy agradable y definida en todas partes, pero la solución sólo se define en algún intervalo\((-\infty, C)\) o\((C, \infty)\). Por lo general, cuando esto sucede solo consideramos uno de estos la solución. Por ejemplo si imponemos una condición\(y(0) = 1\), entonces la solución es\(y=\frac{1}{1-x}\), y consideraríamos esta solución sólo para\(x\) en el intervalo\((-\infty,1)\). En la figura, es el lado izquierdo de la gráfica.
Los problemas clásicos que conducen a ecuaciones diferenciales solucionables por integración son problemas relacionados con la velocidad, la aceleración y la distancia. Seguramente has visto estos problemas antes en tu clase de cálculo.
Supongamos que un automóvil conduce a una velocidad\(e^{t/2}\) meters per second, where \(t\) is time in seconds. How far did the car get in 2 seconds (starting at \(t = 0\))? How far in 10 seconds?
Solución
Dejar\(x\) denotar la distancia recorrida por el auto. La ecuación es
\[x' = e^{t/2} \nonumber \]
Podemos simplemente integrar esta ecuación para conseguir que
\[x(t) = 2e^{t/2} + C \nonumber \]
Todavía tenemos que averiguarlo\(C\). Sabemos que cuando\(t = 0\), entonces\(x = 0\). Es decir,\(x(0) = 0\). Entonces
\[ 0 = x(0) = 2 e^{0/2} + C = 2 + C \nonumber \]
Así\(C = -2\) y
\[x(t) = 2 e^{t/2} - 2 \nonumber \]
Ahora solo nos conectamos para llegar donde está el auto a los 2 y a los 10 segundos. Obtenemos
\[x(2) = 2e^{2/2} - 2 \approx 3.44 \text{~meters},~~~ x(10) = 2e^{10/2} - 2 \approx 294\text{~meters} \nonumber \]
Supongamos que el auto acelera a un ritmo de\(t^2 \frac{m}{s^2}\). En el tiempo\(t = 0\) the car is at the 1 meter mark and is traveling at 10 m/s. Dónde está el auto en el momento\(t = 10\).
Solución
Bueno, esto es en realidad un problema de segundo orden. Si\(x\) es la distancia recorrida, entonces\(x'\) es la velocidad, y\(x''\) es la aceleración. La ecuación con condiciones iniciales es
\[x'' = t^2, \quad x(0) = 1, \quad x'(0) = 10 \nonumber \]
Y si decimos\(x' = v\). Entonces tenemos el problema
\[v' = t^2, \quad v(0) = 10 \nonumber \]
Una vez que resolvamos para\(v\), podemos integrar y encontrar\(x\).


